Zagadnienia
4. Miara martyngałowa dla rynku skończonego
Wyznaczenie ceny arbitrażowej osiągalnej wypłaty ![]() poprzez
znalezienie strategii replikującej jest często bardzo trudne,
szczególnie gdy mamy długi horyzont czasowy
poprzez
znalezienie strategii replikującej jest często bardzo trudne,
szczególnie gdy mamy długi horyzont czasowy ![]() i dużo scenariuszy.
i dużo scenariuszy.
Przedstawimy teraz alternatywne podejście do tego problemu —
metodę martyngałową. Spotkaliśmy się już z nią w rozdz. 2, w którym
była przedstawiona jako jedna z możliwych metod wyceny, choć nie
było widać jej zalet w porównaniu z metodą replikacji. Do badania
rynku skończonego, a więc bardziej skomplikowanego, okaże się ona
bardzo przydatna. Metoda ta pozwala na wypisanie jawnych wzorów na
![]() za pomocą wartości oczekiwanych.
za pomocą wartości oczekiwanych.
4.1. Dyskontowanie
Często przy badaniu rynków finansowych wyróżniamy instrument
pierwotny o numerze 0, którego zadaniem jest mierzenie wartości
pieniądza w czasie (proces dyskontujący, czynnik dyskontujący, numéraire). My przyjmiemy, że ![]() odpowiada lokacie
pieniędzy w banku na znany procent
odpowiada lokacie
pieniędzy w banku na znany procent ![]() tzn.
tzn. ![]() . W dalszym
ciągu na oznaczenie rynku będziemy stosowali wymiennie
. W dalszym
ciągu na oznaczenie rynku będziemy stosowali wymiennie ![]() lub
lub ![]() lub
lub ![]() . Dysponując procesem dyskontującym
wprowadzimy pojęcie zdyskontowanego procesu cen:
. Dysponując procesem dyskontującym
wprowadzimy pojęcie zdyskontowanego procesu cen:
Definicja 4.1
Wektor ![]() , gdzie
, gdzie
![]() dla
dla ![]() ,
nazwiemy zdyskontowanym procesem cen.
,
nazwiemy zdyskontowanym procesem cen.
Okazuje się, że samofinansowalność strategii można sprawdzić badając zachowanie zdyskontowanego procesu bogactwa.
Lemat 4.1
Strategia ![]() jest samofinansująca
się wtedy i tylko wtedy, gdy dla wszystkich
jest samofinansująca
się wtedy i tylko wtedy, gdy dla wszystkich ![]() zachodzi
równość
zachodzi
równość![]()
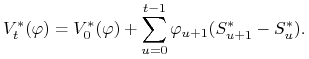 |
(4.1) |
Ustalmy strategię ![]() . Warunek
. Warunek ![]() oznacza
z definicji
oznacza
z definicji
który jest równoważny warunkowi
co z kolei jest równoważne, jak pokazaliśmy w dowodzie tw.
3.1 (udowodnionego dla dowolnych cen ![]() , a więc możemy
wziąć
, a więc możemy
wziąć ![]() zamiast
zamiast ![]() ) faktowi:
) faktowi:
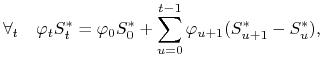 |
a jest to warunek (4.1), gdyż ![]() .
.
Z lematu 4.1 wynika
Wniosek 4.1
Strategia ![]() jest samofinansująca się wtedy i tylko wtedy,
gdy dla wszystkich
jest samofinansująca się wtedy i tylko wtedy,
gdy dla wszystkich ![]() zachodzi:
zachodzi:
| (4.2) |
Wniosek 4.2
Zmiana czynnika dyskontującego nie zmienia klasy portfeli samofinansujących się.
W lemacie 4.1 rozpatrzone zostało dyskontowanie
przez proces ![]() , ale to samo zachodzi, gdy weźmiemy dowolne
, ale to samo zachodzi, gdy weźmiemy dowolne ![]() ,
takie że
,
takie że ![]() dla każdego
dla każdego ![]() , gdyż następujące warunki są równoważne:
, gdyż następujące warunki są równoważne:
-
i)
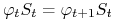 dla każdego
dla każdego 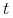 ,
, -
ii)
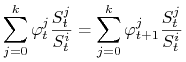 dla każdego
dla każdego 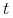 ,
, -
iii)
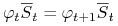 dla każdego
dla każdego 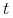 , gdzie
, gdzie 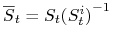 .
.
Ta uwaga jest przydatna, gdyż czasami wygodnie jest zmienić jednostki, w których mierzone są wartości instrumentów podstawowych i pochodnych (bierzemy inny proces dyskontujący).
4.2. Miara martyngałowa, arbitraż
Teraz wprowadzimy podstawowe pojęcie dla rozważań dotyczących wyceny, a mianowicie pojęcie miary martyngałowej.
Definicja 4.2
Miarę probabilistyczną ![]() na
na
![]() równoważną z
równoważną z ![]() nazywa się miarą
martyngałową dla
nazywa się miarą
martyngałową dla
-
zdyskontowanego procesu cen
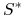 ,
gdy
,
gdy 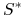 jest
jest 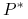 -martyngałem względm filtracji
-martyngałem względm filtracji 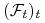 ,
, -
rynku
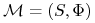 , gdy dla każdej strategii
, gdy dla każdej strategii 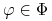 proces
proces 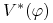 zadany wzorem
zadany wzorem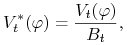
czyli zdyskontowany proces bogactwa, jest
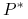 -martyngałem
względm filtracji
-martyngałem
względm filtracji 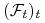 .
.
Symbolem ![]() (odpowiednio
(odpowiednio ![]() )
będziemy oznaczać klasę miar martyngałowych dla procesu
)
będziemy oznaczać klasę miar martyngałowych dla procesu ![]() (odpowiednio dla rynku
(odpowiednio dla rynku ![]() ).
).
Uwaga 4.1
a) Warto zauważyć, że klasy ![]() ,
, ![]() zależą od czynnika dyskontującego. (patrz ćw. 2.12).
zależą od czynnika dyskontującego. (patrz ćw. 2.12).
b) Dla przestrzeni probabilistycznej ![]() o skończonej liczbie
elementów miara probabilistyczna
o skończonej liczbie
elementów miara probabilistyczna ![]() jest równoważna z
jest równoważna z ![]() wtedy i
tylko wtedy, gdy
wtedy i
tylko wtedy, gdy ![]() dla kazdego
dla kazdego ![]() .
.
Wprost z definicji miary martyngałowej dla rynku mamy
Wniosek 4.3
Jeśli ![]() , to dla dowolnego portfela
, to dla dowolnego portfela
![]() i dowolnej chwili
i dowolnej chwili ![]()
| (4.3) |
Okazuje się, że zachodzi równość zbiorów ![]() ,
, ![]() .
.
Twierdzenie 4.1
Miara ![]() jest miarą martyngałową dla rynku
jest miarą martyngałową dla rynku ![]() wtedy
i tylko wtedy, gdy
wtedy
i tylko wtedy, gdy ![]() jest miarą martyngałową dla
zdyskontowanego procesu cen.
jest miarą martyngałową dla
zdyskontowanego procesu cen.
Niech ![]() będzie miarą martyngałową dla procesu cen. Weźmy dowolne
będzie miarą martyngałową dla procesu cen. Weźmy dowolne ![]() . Korzystając
z (4.2) i z prognozowalności
. Korzystając
z (4.2) i z prognozowalności ![]() mamy
mamy
Zatem ![]() jest, dla dowolnego
jest, dla dowolnego ![]() ,
,
![]() -martyngałem względem filtracji
-martyngałem względem filtracji ![]() tzn.
tzn.
![]() .
.
Należy jeszcze udowodnić, że jeśli ![]() jest miarą martyngałową
dla rynku, to jest miarą martyngałową dla procesu cen. Weźmy
strategię
jest miarą martyngałową
dla rynku, to jest miarą martyngałową dla procesu cen. Weźmy
strategię ![]() polegającą na kupnie jednostki
polegającą na kupnie jednostki ![]() -tego
instrumentu bazowego na początku i trzymaniu go do końca, tzn.
-tego
instrumentu bazowego na początku i trzymaniu go do końca, tzn. ![]() ,
, ![]() , dla
, dla ![]() . Jest to strategia samofinansująca się. Zatem
. Jest to strategia samofinansująca się. Zatem
![]() jest
jest ![]() -martyngałem i
-martyngałem i
| (4.4) |
Ponadto zachodzi
zatem z (4.4) mamy
Czyli dla ![]() współrzędna
współrzędna ![]() jest
jest
![]() -martyngałem, tzn.
-martyngałem, tzn. ![]() jest
jest ![]() -martyngałem, więc
-martyngałem, więc
![]() .
.
Twierdzenie to pozwala sprowadzić badanie czy ![]() jest miarą
martyngałową dla rynku, a więc czy dla wszystkich
jest miarą
martyngałową dla rynku, a więc czy dla wszystkich ![]() procesy
procesy ![]() są
są ![]() -martyngałami, do badania czy
proces zdyskontowanych cen, a więc jeden proces, jest
-martyngałami, do badania czy
proces zdyskontowanych cen, a więc jeden proces, jest
![]() –martyngałem. Od tego momentu będziemy mówić o mierze
martyngałowej opuszczając dalsze rozróżnienie, gdyż jest ono
nieistotne.
–martyngałem. Od tego momentu będziemy mówić o mierze
martyngałowej opuszczając dalsze rozróżnienie, gdyż jest ono
nieistotne.
Jak pokazuje następne twierdzenie, badanie możliwości arbitrażu sprowadza się do badania istnienia miar martyngałowych:
Twierdzenie 4.2
(Pierwsze podstawowe twierdzenie matematyki finansowej).
Rynek ![]() jest rynkiem bez
możliwości arbitrażu wtedy i tylko wtedy gdy istnieje miara martyngałowa.
jest rynkiem bez
możliwości arbitrażu wtedy i tylko wtedy gdy istnieje miara martyngałowa.
Dostateczność.
Weźmy ![]() (z założenia takie
(z założenia takie ![]() istnieje). Korzystając z (4.3) otrzymujemy, że na rynku nie
ma możliwości arbitrażu. Istotnie, gdyby istniał arbitraż
istnieje). Korzystając z (4.3) otrzymujemy, że na rynku nie
ma możliwości arbitrażu. Istotnie, gdyby istniał arbitraż ![]() ,
to
,
to ![]() oraz
oraz ![]() i
i ![]() . A że
. A że ![]() , to
, to
a więc prawa strona wzoru (4.3) dla ![]() byłaby dodatnia,
a lewa równałaby się zeru. Sprzeczność.
byłaby dodatnia,
a lewa równałaby się zeru. Sprzeczność.
Zajmiemy
się teraz koniecznością. Zbiór ![]() jest skończony, więc każdą
zmienną losową
jest skończony, więc każdą
zmienną losową ![]() można utożsamiać
z wektorem
można utożsamiać
z wektorem ![]() , gdzie
, gdzie
![]() ,
, ![]() .
I na odwrót, wektor
.
I na odwrót, wektor ![]() wyznacza
zmienną losową
wyznacza
zmienną losową ![]() , a mianowicie przyjmujemy
, a mianowicie przyjmujemy ![]() dla
każdego
dla
każdego ![]() . Niech
. Niech
(przypomnijmy iż ![]() oznacza, że
oznacza, że ![]() dla każdego
dla każdego
![]() ). Każdy element
). Każdy element ![]() wyznacza zmienną losową nieujemną i na
odwrót, każdej zmiennej losowej nieujemnej (poza zmienną losową
równą stale zeru) odpowiada jeden element ze zbioru
wyznacza zmienną losową nieujemną i na
odwrót, każdej zmiennej losowej nieujemnej (poza zmienną losową
równą stale zeru) odpowiada jeden element ze zbioru ![]() . Niech
. Niech
Zatem elementem ![]() jest, przy zastosowaniu utożsamienia opisanego
powyżej, zdyskontowany zysk w chwili
jest, przy zastosowaniu utożsamienia opisanego
powyżej, zdyskontowany zysk w chwili ![]() , gdy stosujemy strategię
, gdy stosujemy strategię
![]() , dla której kapitał początkowy jest równy zeru, czyli
elementami
, dla której kapitał początkowy jest równy zeru, czyli
elementami ![]() są zdyskontowane zyski (w chwili
są zdyskontowane zyski (w chwili ![]() ) strategii
) strategii
![]() , których kapitał początkowy jest równy zeru.
, których kapitał początkowy jest równy zeru.
Jak łatwo zauważyć, fakt nieistnienia arbitrażu można zapisać
w terminach ![]() i
i ![]() , a mianowicie
, a mianowicie
Zatem z założeń twierdzenia wynika, że ![]() .
Ponadto
.
Ponadto ![]() jest liniową podprzestrzenią
jest liniową podprzestrzenią ![]() , a
, a
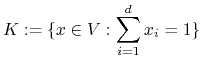 |
jest zbiorem zwartym i wypukłym. Oczywiście ![]() , więc
, więc ![]() . Korzystając z twierdzenia o oddzielaniu można
ściśle oddzielić zbiór zwarty i wypukły od podprzestrzeni liniowej.
Zatem istnieje
. Korzystając z twierdzenia o oddzielaniu można
ściśle oddzielić zbiór zwarty i wypukły od podprzestrzeni liniowej.
Zatem istnieje ![]() (tj. element
(tj. element ![]() ortogonalny do
ortogonalny do ![]() ,
czyli taki że
,
czyli taki że ![]() ,
, ![]() ), taki że:
), taki że:
| (4.5) |
Wektor ![]() mający
mający ![]() na
na ![]() -tym miejscu i zero na pozostałych
należy do
-tym miejscu i zero na pozostałych
należy do ![]() , więc z (4.5) mamy
, więc z (4.5) mamy ![]() .
Zdefiniujmy miarę probabilistyczną
.
Zdefiniujmy miarę probabilistyczną
gdzie ![]() Jest ona równoważna z
Jest ona równoważna z ![]() (bo
(bo
![]() dla każdego
dla każdego ![]() ). Teraz wykażemy, że
). Teraz wykażemy, że
![]() jest miarą martyngałową. Dla dowolnego procesu
prognozowalnego
jest miarą martyngałową. Dla dowolnego procesu
prognozowalnego ![]() , korzystając
z tw. 3.2 dobieramy proces prognozowalny
, korzystając
z tw. 3.2 dobieramy proces prognozowalny ![]() ,
taki że
,
taki że ![]() jest portfelem
samofinansującym się o kapitale początkowym równym zeru. Wtedy
oczywiście
jest portfelem
samofinansującym się o kapitale początkowym równym zeru. Wtedy
oczywiście
a ponieważ ![]() , więc
, więc
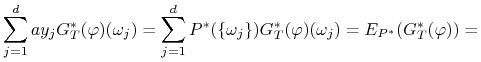 |
||||
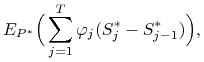 |
przy czym w ostatniej równości skorzystaliśmy z lematu
4.1. Stąd wynika, że dla każdego ![]() i dla dowolnego procesu prognozowalnego ograniczonego
i dla dowolnego procesu prognozowalnego ograniczonego ![]() mamy
mamy
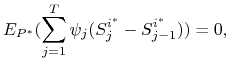 |
a więc ![]() ,
, ![]() , jest
, jest ![]() -martyngałem. Czyli
-martyngałem. Czyli
![]() jest miarą martyngałową.
jest miarą martyngałową.
4.3. Wycena, zupełność rynku, kontrakty forward
Twierdzenie 4.3
Niech ![]() będzie rynkiem bez możliwości arbitrażu.
Wtedy cena arbitrażowa w chwili
będzie rynkiem bez możliwości arbitrażu.
Wtedy cena arbitrażowa w chwili ![]() osiągalnej na rynku
osiągalnej na rynku ![]() wypłaty
wypłaty ![]() jest dana wzorem
jest dana wzorem
| (4.6) |
dla dowolnej miary martyngałowej ![]() .
.
Aby udowodnić (4.6), weźmy strategię ![]() replikującą
wypłatę
replikującą
wypłatę ![]() . Wtedy z definicji ceny arbitrażowej, z (4.3)
i z tego, że
. Wtedy z definicji ceny arbitrażowej, z (4.3)
i z tego, że ![]() otrzymujemy:
otrzymujemy:
Ponieważ proces replikujący ![]() jest wyznaczony
jednoznacznie i równość (4.3) jest prawdziwa dla każdej
miary
jest wyznaczony
jednoznacznie i równość (4.3) jest prawdziwa dla każdej
miary ![]() , więc wzór (4.6) nie
zależy od wyboru miary martyngałowej dla rynku.
, więc wzór (4.6) nie
zależy od wyboru miary martyngałowej dla rynku.
Wzór (4.6) nazywamy wzorem martyngałowym na cenę lub formułą wyceny w warunkach powszechnej obojętności względem ryzyka. W szczególności z (4.6) i liniowości wartości oczekiwanej wynika
Uwaga 4.2
Na rynku bez możliwości arbitrażu cena
arbitrażowa jest operatorem liniowym na przestrzeni liniowej wypłat
osiągalnych, czyli gdy ![]() i
i ![]() są wypłatami osiągalnymi, to
są wypłatami osiągalnymi, to
| (4.7) |
Wniosek 4.2 można też otrzymać korzystając z definicji ceny arbitrażowej i własności iloczynu skalarnego.
Wniosek 4.4
(Parytet kupna-sprzedaży). Na rynku bez możliwości
arbitrażu, gdy europejskie opcje kupna i sprzedaży (dla tej samej
akcji) z tą samą ceną wykonania ![]() są osiągalne, to ich ceny są
związane wzorem:
są osiągalne, to ich ceny są
związane wzorem:
| (4.8) |
gdzie ![]()
![]() odp.
odp. ![]() oznacza cenę w chwili
oznacza cenę w chwili ![]() europejskiej opcji kupna
europejskiej opcji kupna ![]() odp. sprzedaży
odp. sprzedaży![]() z ceną wykonania
z ceną wykonania ![]() .
.
Z tw. 4.2 łatwo wynika
Wniosek 4.5
na rynku bez możliwości arbitrażu wycena wypłaty osiągalnej za
pomocą ceny arbitrażowej (wzoru (4.6)) tworzy zgodny system
cen, w tym sensie, że rynek rozszerzony o instrument bazowy o cenie
![]() jest dalej rynkiem bez możliwości arbitrażu.
jest dalej rynkiem bez możliwości arbitrażu.
Ćwiczenie 4.1
Udowodnić wniosek 4.5.
Z własności (4.7) często korzysta się, gdy wypłatę potrafimy przedstawić jako kombinację lub jako granicę kombinacji wypłat, które potrafimy wycenić.
Przykład 4.1
Znajdziemy na rynku bez możliwości arbitrażu
ceny wypłat w chwili ![]() związanych z instrumentem podstawowym
o cenie
związanych z instrumentem podstawowym
o cenie ![]() (tj.
(tj. ![]() dla pewnego
dla pewnego ![]() ) w następujący
sposób:
) w następujący
sposób:
-
a)
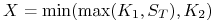 (jest to tzw. opcja
collar),
(jest to tzw. opcja
collar), -
b)
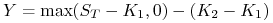 , (jest to tzw. opcja bostońska),
, (jest to tzw. opcja bostońska),
gdzie ![]() i
i ![]() są stałymi, przy założeniu, że wypłaty
są stałymi, przy założeniu, że wypłaty ![]() i
i ![]() są osiągalne.
są osiągalne.
Szukamy profilu wypłat badając własności ![]() (odp.
(odp. ![]() ), tj.
analizując postać wypłaty w zależności od ceny instrumentu bazowego,
na poszczególnych przedziałach (warto zrobić rysunek). Znajdujemy,
że dla
), tj.
analizując postać wypłaty w zależności od ceny instrumentu bazowego,
na poszczególnych przedziałach (warto zrobić rysunek). Znajdujemy,
że dla ![]() :
:
| (4.9) |
a gdy ![]() , to
, to ![]() . Wypłata
. Wypłata ![]() nie zależy od relacji
pomiędzy
nie zależy od relacji
pomiędzy ![]() i
i ![]() :
:
Stąd i z liniowości ceny otrzymujemy:
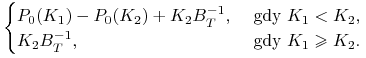 |
||||
Oczywiście profil wypłat może mieć różne przedstawienia, np. ![]() można dla
można dla ![]() przedstawić w postaci
przedstawić w postaci
| (4.10) |
ale (4.9) i (4.10) prowadzą do tej samej ceny (co widać z parytetu).
Przykład 4.2
a) Rozpatrzmy rynek jednookresowy z trzema możliwymi zdarzeniami losowymi. Inwestor uważa, że są one jednakowo prawdopodobne. Na rynku stopa procentowa bez ryzyka wynosi 20% i jest jedna akcja mająca proces cen postaci:
Zbadajmy, czy na tym rynku istnieje arbitraż.
Oczywiście przy badaniu własności tego rynku nie jest istotna opinia inwestora o szansach scenariuszy. W celu zbadania, czy na tym rynku istnieje arbitraż, zbadamy, czy istnieje miara martyngałowa. Rynek jest jednookresowy, więc szukamy rozwiązania układu:
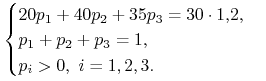 |
Rozwiązanie ma postać
przy czym ![]() . Zatem istnieje nieskończenie
wiele miar martyngałowych, czyli nie istnieje arbitraż.
. Zatem istnieje nieskończenie
wiele miar martyngałowych, czyli nie istnieje arbitraż.
b) Co będzie, gdy na rynku pojawi się jeszcze jedna akcja:
Teraz trzeba szukać rozwiązania układu:
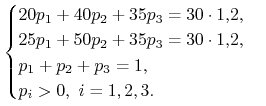 |
Ponieważ z pierwszych trzech równań otrzymujemy, że ![]() i
i ![]() , więc nie istnieje rozwiązanie spełniające
, więc nie istnieje rozwiązanie spełniające ![]() ,
,
![]() . Zatem na rynku istnieje arbitraż. Znajdziemy teraz
postać portfela arbitrażowego. Szukamy portfela
. Zatem na rynku istnieje arbitraż. Znajdziemy teraz
postać portfela arbitrażowego. Szukamy portfela ![]() takiego, że
takiego, że
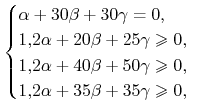 |
przy czym choć jedna nierówność jest ostra. Stąd otrzymujemy, że
jest portfelem arbitrażowym np. portfel ![]() jest
arbitrażem.
jest
arbitrażem.
Gdy się przyjrzeć dokładniej cenom, to widać, że ![]() i w
chwili 1 ceny drugiej akcji są nie mniejsze od cen pierwszej, skąd
wynika natychmiast, że portfel
i w
chwili 1 ceny drugiej akcji są nie mniejsze od cen pierwszej, skąd
wynika natychmiast, że portfel ![]() jest arbitrażem.
jest arbitrażem.
Uwaga 4.3
Powyższy przykład ilustruje fakt, że przy połączeniu dwóch rynków bez możliwości arbitrażu (w jeden) może się zdarzyć, że otrzymany rynek stanie się rynkiem z arbitrażem.
Gdy mamy rynek bez możliwości arbitrażu, to następnym pojawiającym się pytaniem jest pytanie o wypłaty osiągalne, gdyż takie wypłaty umiemy wyceniać. Okazuje się, że patrząc na zbiór miar martyngałowych potrafimy określić kiedy wszystkie wypłaty są osiągalne.
Definicja 4.3
Rynek ![]() nazywamy zupełnym, gdy
każda wypłata jest osiągalna na tym rynku.
nazywamy zupełnym, gdy
każda wypłata jest osiągalna na tym rynku.
Twierdzenie 4.4
(Drugie podstawowe twierdzenie matematyki finansowej). Rynek bez możliwości arbitrażu jest zupełny wtedy i tylko wtedy, gdy istnieje dokładnie jedna miara martyngałowa.
Konieczność. Niech ![]() będzie dowolną zmienną losową,
a więc dowolną wypłatą. Wypłata
będzie dowolną zmienną losową,
a więc dowolną wypłatą. Wypłata ![]() jest osiągalna (bo rynek
jest zupełny). Także
jest osiągalna (bo rynek
jest zupełny). Także ![]() (co wynika
z braku możliwości arbitrażu i tw. 4.2).
Zatem dla
(co wynika
z braku możliwości arbitrażu i tw. 4.2).
Zatem dla ![]() mamy
mamy
Gdy miary ![]() , to
, to
Stąd, biorąc ![]() , dla
, dla ![]() , mamy
, mamy
Wobec dowolności ![]() , a więc i
, a więc i ![]() mamy
mamy ![]() .
.
Dostateczność. Dowód nie wprost. Załóżmy, że rynek jest
niezupełny. Wtedy istnieje nieosiągalna wypłata ![]() . Niech
. Niech ![]() będzie klasą zmiennych losowych zdefiniowaną następująco
będzie klasą zmiennych losowych zdefiniowaną następująco
Zatem ![]() jest zbiorem zdyskontowanych wypłat otrzymanych za
pomocą strategii samofinansujących się przy dopuszczeniu dowolnego
kapitału początkowego.
jest zbiorem zdyskontowanych wypłat otrzymanych za
pomocą strategii samofinansujących się przy dopuszczeniu dowolnego
kapitału początkowego. ![]() jest podzbiorem właściwym zbioru
wszystkich zmiennych losowych
jest podzbiorem właściwym zbioru
wszystkich zmiennych losowych ![]() , gdyż
, gdyż ![]() nie
należy do
nie
należy do ![]() . Istotnie, gdyby
. Istotnie, gdyby ![]() należało do
należało do ![]() , to
, to
dla pewnego ![]() , a więc z lematu 4.1
zachodziłoby
, a więc z lematu 4.1
zachodziłoby ![]() , czyli
, czyli ![]() , zatem
, zatem ![]() byłoby osiągalne.
byłoby osiągalne.
Niech ![]() będzie miarą martyngałową. Wszystkie zmienne losowe są
będzie miarą martyngałową. Wszystkie zmienne losowe są
![]() –całkowalne z kwadratem (bo
–całkowalne z kwadratem (bo ![]() jest zbiorem
skończonym) i możemy zdefiniować iloczyn skalarny wzorem
jest zbiorem
skończonym) i możemy zdefiniować iloczyn skalarny wzorem
Ponieważ ![]() jest podprzestrzenią liniową
jest podprzestrzenią liniową ![]() oraz
oraz
![]() , więc istnieje zmienna losowa
, więc istnieje zmienna losowa ![]() różna od 0, ortogonalna do
różna od 0, ortogonalna do ![]() . Ponieważ
. Ponieważ ![]() (bierzemy kapitał początkowy
(bierzemy kapitał początkowy ![]() i nic nie robimy, czyli
i nic nie robimy, czyli
![]() ,
, ![]() ), więc zmienna losowa
), więc zmienna losowa ![]() , jako ortogonalna do
, jako ortogonalna do
![]() , ma średnią zero
, ma średnią zero
| (4.11) |
Zdefiniujmy miarę probabilistyczną ![]() na podzbiorach
na podzbiorach ![]() wzorem
wzorem
| (4.12) |
gdzie ![]() .
. ![]() jest miarą
probabilistyczną równoważną z
jest miarą
probabilistyczną równoważną z ![]() , bo
, bo ![]() dla
każdej
dla
każdej ![]() i z (4.11) otrzymujemy
i z (4.11) otrzymujemy
Oczywiście ![]() , bo
, bo ![]() jest zmienną losową niezerową. Udowodnimy teraz, że
jest zmienną losową niezerową. Udowodnimy teraz, że
![]() jest miarą martyngałową.
jest miarą martyngałową.
W tym celu weźmy dowolny proces prognozowalny ![]() .
Korzystając z tw. 3.2 dobieramy proces prognozowalny
.
Korzystając z tw. 3.2 dobieramy proces prognozowalny
![]() , taki że
, taki że ![]() jest portfelem
samofinansującym się o zerowym kapitale początkowym. Z definicji
jest portfelem
samofinansującym się o zerowym kapitale początkowym. Z definicji ![]() otrzymujemy
otrzymujemy
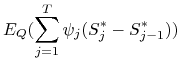 |
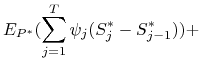 |
(4.13) | |||
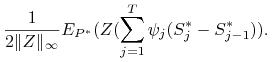 |
Pierwszy składnik z prawej strony wzoru (4.13) jest równy
zero, gdyż ![]() jest
jest ![]() martyngałem.
Drugi składnik sumy z prawej strony (4.13) jest także równy
zeru, gdyż
martyngałem.
Drugi składnik sumy z prawej strony (4.13) jest także równy
zeru, gdyż
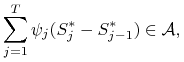 |
a ![]() jest zmienną losową ortogonalną do
jest zmienną losową ortogonalną do ![]() w
w ![]() .
Zatem
.
Zatem ![]() jest
jest ![]() -martyngałem, a więc
-martyngałem, a więc ![]() jest miarą
martyngałową różną od
jest miarą
martyngałową różną od ![]() . Otrzymaliśmy sprzeczność
z założeniem, że istnieje dokładnie jedna miara
martyngałowa.
. Otrzymaliśmy sprzeczność
z założeniem, że istnieje dokładnie jedna miara
martyngałowa.
Podkreślmy jeszcze raz, że zupełność jest bardzo ważną cechą rynku,
gdyż na takim rynku potrafimy wycenić w sposób jednoznaczny każdą
wypłatę, a ponadto korzystając z faktu, że twierdzenie
o reprezentacji martyngałów (zachodzące, gdy ![]() i czas są
skończone) jest równoważne zupełności (patrz zad.4.6) można,
korzystając z lematu 4.1 i twierdzenia o reprezentacji
martyngałów, znaleźć strategię replikującą dla każdej wypłaty na
rynku zupełnym.
i czas są
skończone) jest równoważne zupełności (patrz zad.4.6) można,
korzystając z lematu 4.1 i twierdzenia o reprezentacji
martyngałów, znaleźć strategię replikującą dla każdej wypłaty na
rynku zupełnym.
Teraz podamy przykłady zastosowań udowodnionych przed chwilą twierdzeń.
Przykład 4.3
Rozważmy rynek z przykł. 4.2a. Jak widzieliśmy na tym rynku istnieje wiele miar martyngałowych, czyli rynek jest wolny od możliwości arbitrażu i nie wszystkie wypłaty są osiągalne.
Wypłata ![]() jest osiągalna, gdy istnieje portfel
replikujący
jest osiągalna, gdy istnieje portfel
replikujący ![]() , tj.
, tj. ![]() ,
czyli musi zachodzić:
,
czyli musi zachodzić:
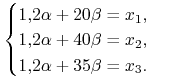 |
Stąd otrzymujemy, że wypłaty osiągalne spełniają warunek:
| (4.14) |
Wycenimy teraz wypłatę osiągalną. Korzystając z (4.6) i (4.14) mamy:
| (4.15) | |||||
| (4.16) |
a więc widzimy, że cena nie zależy od wyboru miary martyngałowej (co
i tak było udowodnione w tw. 4.3). Wzór (4.15)
sugeruje, że można w inny sposób znajdować wypłaty osiągalne.
Mianowicie, cena zadana wzorem (4.15) nie może zależeć od
parametru ![]() (tw. 4.3), więc współczynnik przy
(tw. 4.3), więc współczynnik przy ![]() w (4.16) powinien się zerować. Jest to sugestia, którą
udowodnimy w tw 4.5. I w ten sposób znowu dochodzimy do
warunku (4.14).
w (4.16) powinien się zerować. Jest to sugestia, którą
udowodnimy w tw 4.5. I w ten sposób znowu dochodzimy do
warunku (4.14).
Przykł. 4.3 sugeruje, że można udowodnić bardzo przydatną charakteryzację wypłat osiągalnych:
Twierdzenie 4.5
Gdy rynek jest wolny od
arbitrażu, to wypłata ![]() jest osiągalna wtedy i tylko wtedy, gdy
funkcja
jest osiągalna wtedy i tylko wtedy, gdy
funkcja ![]() zadana wzorem
zadana wzorem
jest stała.
Konieczność została udowodniona w tw. 4.3, a dostateczność pozostawiamy jako zadanie.
∎Ćwiczenie 4.2
Na rynku dwuokresowym o czterech możliwych
scenariuszach stopa procentowa bez ryzyka wynosi 10%. Na tym rynku
jest jedna akcja, której ceny są opisane przez proces ![]() :
:
Znaleźć ceny europejskich opcji kupna i sprzedaży z ceną wykonania
![]() .
.
Zaczniemy od sprawdzenia, czy rynek jest wolny od arbitrażu.
Znajdujemy miarę martyngałową ![]() na
na ![]() , a mianowicie
, a mianowicie
Miara martyngałowa jest jedyna, więc każda wypłata jest osiągalna. Ze wzoru (4.6) otrzymujemy
oraz
Oczywiście obliczając wartość ![]() można było skorzystać
z parytetu.
można było skorzystać
z parytetu.
Wycena kontraktu terminowego forward. Zajmiemy się teraz na
rynku bez możliwości arbitrażu wyceną kontraktu terminowego forward
na ![]() -ty instrument o cenie
-ty instrument o cenie ![]() . Wartość tego kontraktu forward
w chwili
. Wartość tego kontraktu forward
w chwili ![]() będziemy oznaczać przez
będziemy oznaczać przez ![]() . Kontrakt terminowy
forward jest zadany przez wypłatę
. Kontrakt terminowy
forward jest zadany przez wypłatę ![]() , gdzie
, gdzie ![]() jest ceną
forward. Wypłata
jest ceną
forward. Wypłata ![]() jest osiągalna, zatem ze wzoru (4.6)
znajdujemy cenę w chwili
jest osiągalna, zatem ze wzoru (4.6)
znajdujemy cenę w chwili ![]() wypłaty
wypłaty ![]()
| (4.17) |
Jak wiemy, cena forward ![]() jest taką liczbą, że wartość kontraktu
forward w chwili zero jest równa zeru, tj.
jest taką liczbą, że wartość kontraktu
forward w chwili zero jest równa zeru, tj. ![]() , zatem ze
wzoru (4.17) otrzymujemy, że cena forward wynosi
, zatem ze
wzoru (4.17) otrzymujemy, że cena forward wynosi
Warto podkreślić, że cena
forward nie ulega zmianie w czasie trwania kontraktu, natomiast
wartość kontraktu (równa zeru w chwili zawierania) zmienia się
w czasie, w szczególności zwykle jest niezerowa w chwili dostawy
(rozliczania). Wstawiając do wzoru (4.17) cenę forward ![]() mamy
mamy
Twierdzenie 4.6
Wartość kontraktu terminowego forward na ![]() -ty instrument bazowy
wynosi w chwili
-ty instrument bazowy
wynosi w chwili ![]()
4.4. Zagadnienia i zadania na ćwiczenia
Ćwiczenie 4.3
Zanalizować rynek, czyli znaleźć wszystkie miary martyngałowe i wypłaty osiągalne ew. strategie arbitrażowe, gdy rynek jest jednookresowy z trzema możliwymi zdarzeniami losowymi i z aktywami opisanymi w następujący sposób:
a) Na rynku jest 1 akcja, a oprocentowanie wynosi 10%. Ceny akcji są opisane przez
b) Stopa procentowa bez ryzyka wynosi 10% i na rynku są 2 akcje przyjmujące wartości:
a) Nie warto sprawdzać, czy istnieje miara martyngałowa, wystarczy
zauważyć, że zawsze ![]() . Portfele postaci
. Portfele postaci
![]() akcji i
akcji i ![]() jednostek w banku są portfelami
arbitrażowymi.
jednostek w banku są portfelami
arbitrażowymi.
b) Istnieje dokładnie jedna miara martyngałowa: ![]() ,
,
![]() ,
, ![]() . Zatem rynek jest zupełny i wszystkie
wypłaty są osiągalne.
. Zatem rynek jest zupełny i wszystkie
wypłaty są osiągalne.
Ćwiczenie 4.4
Załóżmy, że rynek jednookresowy jest bezarbitrażowy. Udowodnić, że
rynek jest zupełny wtedy i tylko wtedy, gdy liczba stanów
w ![]() (czyli scenariuszy) jest równa liczbie liniowo
niezależnych wektorów wśród wektorów
(czyli scenariuszy) jest równa liczbie liniowo
niezależnych wektorów wśród wektorów ![]()
Rozpatrzmy macierz
![A=\left[\begin{array}[]{cccc}B_{1}(\omega _{1})&S_{1}^{1}(\omega _{1})&\cdots&S_{1}^{k}(\omega _{1})\\
B_{1}(\omega _{2})&\cdots&\ddots&\vdots\\
\vdots&\ddots&\ddots&\vdots\\
B_{1}(\omega _{d})&S_{1}^{1}(\omega _{d})&\cdots&S_{1}^{k}(\omega _{d})\\
\end{array}\right]](wyklady/ip1/mi/mi620.png) |
Rynek jest zupełny wtedy i tylko wtedy, gdy równanie ![]() ma rozwiązanie dla każdego
ma rozwiązanie dla każdego ![]() , co jest równoznaczne z warunkiem
, co jest równoznaczne z warunkiem ![]() , tj. z istnieniem
, tj. z istnieniem ![]() liniowo niezależnych kolumn
macierzy
liniowo niezależnych kolumn
macierzy ![]() .
.
Ćwiczenie 4.5
Niech rynek będzie wolny od arbitrażu. Udowodnić, że jeśli funkcja
![]() dla
dla ![]() jest stała, to
wypłata
jest stała, to
wypłata ![]() jest osiągalna.
jest osiągalna.
Skorzystać z idei drugiego podstawowego twierdzenia matematyki finansowej (tw. 4.4).
Ćwiczenie 4.6
Udowodnić, że rynek bez możliwości arbitrażu jest zupełny wtedy
i tylko wtedy, gdy każdy proces ![]() , który jest
, który jest ![]() -martyngałem
dla pewnego
-martyngałem
dla pewnego ![]() można przedstawić
w postaci
można przedstawić
w postaci
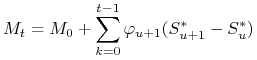 |
(4.18) |
dla ![]() , gdzie
, gdzie ![]() jest procesem
prognozowalnym.
jest procesem
prognozowalnym.
W następnym zadaniu podajemy przykład ilustrujący fakt, że na rynku jednookresowym o przeliczalnej liczbie scenariuszy i aktywów może nie istnieć ani arbitraż, ani miara martyngałowa.
Ćwiczenie 4.7
Niech ![]() ,
, ![]() ,
a prawdopodobieństwo
,
a prawdopodobieństwo ![]() będzie takie że
będzie takie że ![]() Rozważmy rynek jednookresowy, na którym stopa procentowa bez ryzyka
Rozważmy rynek jednookresowy, na którym stopa procentowa bez ryzyka
![]() . Ponadto na tym rynku jest przeliczalnie wiele aktywów,
których ceny w chwili 0 są równe 1, tj. ceny spełniają
. Ponadto na tym rynku jest przeliczalnie wiele aktywów,
których ceny w chwili 0 są równe 1, tj. ceny spełniają ![]() dla
dla ![]() , a w chwili końcowej
, a w chwili końcowej ![]() :
:
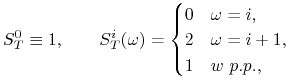 |
dla ![]() . Ceny są elementami
. Ceny są elementami ![]() , więc portfele
na tym rynku są elementami
, więc portfele
na tym rynku są elementami ![]() . Udowodnić, że przy powyższych
założeniach nie istnieje ani arbitraż, ani miara martyngałowa.
. Udowodnić, że przy powyższych
założeniach nie istnieje ani arbitraż, ani miara martyngałowa.
Zaczniemy od wykazania, że nie istnieje arbitraż. Rozpatrzmy
portfel ![]() taki, że
taki, że
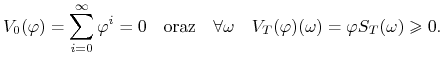 |
(4.19) |
Wtedy z (4.19) biorąc ![]() otrzymujemy
otrzymujemy
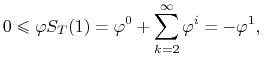 |
a gdy ![]() , to
, to
Stąd ![]() oraz dla każdego
oraz dla każdego ![]() mamy
mamy ![]() , tj.
, tj.
Stąd z kolei ![]() , ponieważ
, ponieważ ![]() ,
a więc
,
a więc ![]() . Zatem nie
istnieje arbitraż.
. Zatem nie
istnieje arbitraż.
Nie istnieje także miara martyngałowa: nie istnieje ![]() takie, że
takie, że
![]() i
i
| (4.20) |
Istotnie, równość (4.20) oznacza, że dla ustalonego ![]() mamy
mamy
Stąd z kolei otrzymujemy, że (4.20) pociąga za sobą
| (4.21) |
Doszliśmy do sprzeczności, gdyż nie istnieje miara probabilistyczna
określona na całej ![]() spełniająca (4.21).
spełniająca (4.21).
Ćwiczenie 4.8
Udowodnić, że na rynku bez możliwości arbitrażu wycena wypłaty osiągalnej za
pomocą ceny arbitrażowej (wzoru (4.6)) tworzy zgodny system
cen, w tym sensie, że rynek rozszerzony o instrument bazowy o cenie
![]() jest dalej rynkiem bez możliwości arbitrażu.
jest dalej rynkiem bez możliwości arbitrażu.
Gdy ![]() , to
, to ![]() są
są
![]() -martyngałami. Ponadto, z (4.6)
-martyngałami. Ponadto, z (4.6)
więc ![]() jest też
jest też ![]() -martyngałem, czyli
-martyngałem, czyli ![]() jest
miarą martyngałowa dla rynku rozszerzonego.
jest
miarą martyngałowa dla rynku rozszerzonego.
Ćwiczenie 4.9
Na rynku dwuokresowym opisanym w ćwiczeniu 4.2 znaleźć
strategię replikującą europejską opcję kupna z ceną wykonania
![]() .
.
Należy zabezpieczyć wypłatę ![]() przyjmującą wartości:
przyjmującą wartości:
![]() ,
, ![]() dla
dla ![]() . Trzeba znaleźć
strategię samofinansującą się
. Trzeba znaleźć
strategię samofinansującą się ![]() replikującą wypłatę
replikującą wypłatę ![]() .
Czyli szukamy
.
Czyli szukamy ![]() , gdzie
, gdzie
![]() oraz
oraz ![]() , gdzie
, gdzie
![]() ,
,
![]() i
i ![]() ,
,
![]() , takich że
, takich że
![]() , tj.
, tj.
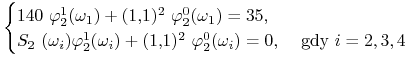 |
oraz
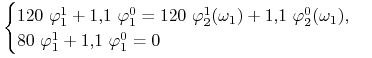 |
(warunek samofinansowania się strategii). Rozwiązując te układy
otrzymujemy: ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.