Zagadnienia
6. Uogólnienia ceny arbitrażowej
Dla wypłat nieosiągalnych nie mamy zdefiniowanej ceny. Teraz
spróbujemy rozszerzyć pojęcie ceny, by móc wyceniać wypłaty
nieosiągalne.
Na rynku bez możliwości arbitrażu cenę instrumentu osiągalnego można
wyliczyć korzystając z pojęcia miary martyngałowej (wzór
(4.6)). Tę wielkość chciałoby się przyjąć jako cenę wypłaty
nieosiągalnej, choć nie widać sensu ekonomicznego takiego
postępowania. Ale dla wypłat nieosiągalnych wielkość ![]() zależy od wyboru miary martyngałowej
zależy od wyboru miary martyngałowej ![]() (patrz przykł.
4.2a). Dlatego dla wypłat nieosiągalnych musimy postępować
inaczej. Będziemy naśladować postępowanie z ćwiczenia
2.15 wprowadzające pojęcie zabezpieczenia doskonałego.
Pozwoli to wprowadzić pojęcia ceny kupującego
i ceny sprzedającego będące rozszerzeniem ceny arbitrażowej.
(patrz przykł.
4.2a). Dlatego dla wypłat nieosiągalnych musimy postępować
inaczej. Będziemy naśladować postępowanie z ćwiczenia
2.15 wprowadzające pojęcie zabezpieczenia doskonałego.
Pozwoli to wprowadzić pojęcia ceny kupującego
i ceny sprzedającego będące rozszerzeniem ceny arbitrażowej.
6.1. Cena sprzedającego i kupującego
Definicja 6.1
Ceną sprzedającego wypłatę ![]() nazywamy wielkość
nazywamy wielkość
| (6.1) |
Jest to najmniejsza wielkość kapitału początkowego pozwalającego
sprzedającemu pokryć swoje zobowiązania bez ryzyka, czyli doskonale
zabezpieczyć wypłatę ![]() , gdyż sprzedający mając tę kwotę
i postępując zgodnie ze strategią
, gdyż sprzedający mając tę kwotę
i postępując zgodnie ze strategią ![]() otrzymuje w chwili
otrzymuje w chwili ![]() ze swojej inwestycji co najmniej
ze swojej inwestycji co najmniej ![]() . Cena sprzedającego
. Cena sprzedającego
![]() jest zawsze skończona, bo wypłata
jest zawsze skończona, bo wypłata ![]() jest ograniczona
przez pewną stałą
jest ograniczona
przez pewną stałą ![]() , a stała jest wypłatą osiągalną mającą
skończoną cenę. Korzystając z definicji infimum możemy otrzymać
warunek równoważny z (6.1):
, a stała jest wypłatą osiągalną mającą
skończoną cenę. Korzystając z definicji infimum możemy otrzymać
warunek równoważny z (6.1):
Gdy sprzedający weźmie zapłatę mniejszą niż ![]() , to
z dodatnim prawdopodobieństwem poniesie stratę.
, to
z dodatnim prawdopodobieństwem poniesie stratę.
Patrząc z drugiej strony na transakcję mamy cenę kupującego. Jest to
maksymalna cena, jaką kupujący jest gotowy zapłacić za walor ![]() .
Jest to maksymalny kapitał taki, że startując z pożyczki równej temu
kapitałowi kupujący jest w stanie znaleźć strategię
.
Jest to maksymalny kapitał taki, że startując z pożyczki równej temu
kapitałowi kupujący jest w stanie znaleźć strategię ![]() generującą kapitał
generującą kapitał ![]() w chwili
w chwili ![]() i taką, że wraz
z wypłatą
i taką, że wraz
z wypłatą ![]() otrzymywaną w chwili
otrzymywaną w chwili ![]() kupujący osiąga pozycję
nieujemną:
kupujący osiąga pozycję
nieujemną:
| (6.2) |
Lemat 6.1
Równoważne sformułowania ceny kupującego:
| (6.3) | ||||
| (6.4) | ||||
| (6.5) |
Z (6.5) wynika, że cenę kupującego można interpretować
jako cenę najdroższej strategii dającej w chwili ![]() wypłatę
mniejszą lub równą wypłacie
wypłatę
mniejszą lub równą wypłacie ![]() .
.
Twierdzenie 6.1
Niech ![]() będzie rynkiem bez możliwości
arbitrażu. Wtedy
będzie rynkiem bez możliwości
arbitrażu. Wtedy
bo z liniowości przestrzeni portfeli mamy ![]() . Z założenia braku arbitrażu
. Z założenia braku arbitrażu ![]() (patrz ćw. 6.2).
(patrz ćw. 6.2).
Dla wypłaty osiągalnej pojęcia ceny kupującego i sprzedającego pokrywają się z ceną arbitrażową. Zatem są rozszerzeniami ceny arbitrażowej na wszystkie wypłaty.
Twierdzenie 6.2
Niech ![]() będzie rynkiem bez możliwości
arbitrażu, a
będzie rynkiem bez możliwości
arbitrażu, a ![]() wypłatą osiągalną. Wtedy
wypłatą osiągalną. Wtedy
Okazuje się, że ceny ![]() i
i ![]() można znaleźć
korzystając z miar martyngałowych.
można znaleźć
korzystając z miar martyngałowych.
Twierdzenie 6.3
Niech ![]() będzie rynkiem bez możliwości arbitrażu. Wtedy
będzie rynkiem bez możliwości arbitrażu. Wtedy
| (6.6) |
 |
(6.7) |
Korzystając z (6.4) wystarczy udowodnić
(6.7) (bo ![]() .
Jeśli wypłata
.
Jeśli wypłata ![]() jest osiągalna, to
jest osiągalna, to ![]() nie
zależy od wyboru miary martyngałowej,
nie
zależy od wyboru miary martyngałowej,
i teza zachodzi na mocy tw. 6.2. Niech ![]() będzie wypłatą
nieosiągalną, a
będzie wypłatą
nieosiągalną, a ![]() osiągalną taką, że
osiągalną taką, że ![]() (takie
(takie ![]() istnieje zawsze, bo zbiór
istnieje zawsze, bo zbiór ![]() jest skończony, więc
jest skończony, więc ![]() ). Wtedy dla każdego
). Wtedy dla każdego ![]() zachodzi
zachodzi
a więc
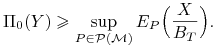 |
(6.8) |
Z (6.8) wobec dowolności ![]() otrzymujemy
otrzymujemy
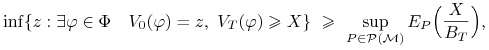 |
czyli
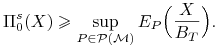 |
Ostatnią część dowodu twierdzenia zostawiamy jako zadanie dla Czytelnika.
∎Wniosek 6.1
Monotoniczność cen Gdy rynek jest
wolny od arbitrażu oraz wypłaty ![]() spełniają
spełniają ![]() , to
, to
Warto zauważyć, że w przeciwieństwie do ceny arbitrażowej ceny kupującego i sprzedającego nie są operatorami liniowymi (patrz ćw. 6.5), czyli rozszerzenia nie zachowują własności liniowości na całej dziedzinie, choć są liniowe na przestrzeni wypłat osiągalnych.
Przykład 6.1
Wróćmy znowu do rynku z przykł. 4.2a. Jak widzieliśmy,
istnieje na nim wiele miar martyngałowych. Postać wypłat osiągalnych
znaleźliśmy w przykł. 4.3. Wypłata ![]() jest
osiągalna, gdy
jest
osiągalna, gdy ![]() .
Znajdziemy teraz cenę kupującego i sprzedającego wypłaty
nieosiągalnej. Załóżmy, że
.
Znajdziemy teraz cenę kupującego i sprzedającego wypłaty
nieosiągalnej. Załóżmy, że
Korzystając z (6.6) mamy:
a z (6.8) mamy:
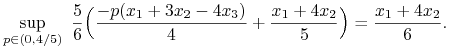 |
Przypadek ![]() rozpatrujemy podobnie.
rozpatrujemy podobnie.
Gdy cena przekracza ![]() , to sprzedający ma możliwość
uzyskania zysku bez ryzyka, a gdy cena jest mniejsza niż
, to sprzedający ma możliwość
uzyskania zysku bez ryzyka, a gdy cena jest mniejsza niż
![]() , to kupujący ma możliwość arbitrażu (patrz ćw.
6.4).
, to kupujący ma możliwość arbitrażu (patrz ćw.
6.4).
6.2. Uogólniona cena arbitrażowa
Możemy na problem wyceny instrumentów nieosiągalnych spojrzeć jeszcze inaczej. Uogólnimy pojęcie ceny arbitrażowej na dowolną wypłatę w następujący sposób:
Definicja 6.2
Liczbę ![]() nazywamy uogólnioną ceną
arbitrażową wypłaty
nazywamy uogólnioną ceną
arbitrażową wypłaty ![]() na rynku
na rynku ![]() wolnym od arbitrażu, gdy istnieje proces adaptowany
wolnym od arbitrażu, gdy istnieje proces adaptowany
![]() taki, że
taki, że
i rynek rozszerzony o instrument o cenie ![]() jest rynkiem bez
możliwości arbitrażu.
jest rynkiem bez
możliwości arbitrażu.
Zatem ![]() jest uogólnioną ceną arbitrażową wypłaty
jest uogólnioną ceną arbitrażową wypłaty ![]() , gdy
sprzedaż wypłaty
, gdy
sprzedaż wypłaty ![]() po cenie
po cenie ![]() nie wprowadza na rynku
możliwości arbitrażu (por. z wnioskiem 4.5). Wtedy proces
nie wprowadza na rynku
możliwości arbitrażu (por. z wnioskiem 4.5). Wtedy proces
![]() jest procesem ceny wypłaty
jest procesem ceny wypłaty ![]() o uogólnionej cenie
arbitrażowej
o uogólnionej cenie
arbitrażowej ![]() . Z tej definicji wynika, że uogólnionych cen
arbitrażowych wypłaty
. Z tej definicji wynika, że uogólnionych cen
arbitrażowych wypłaty ![]() może być wiele. Przez
może być wiele. Przez ![]() będziemy
oznaczać zbiór uogólnionych cen arbitrażowych wypłaty
będziemy
oznaczać zbiór uogólnionych cen arbitrażowych wypłaty ![]() .
.
Twierdzenie 6.4
Weźmy element ![]() . Z pierwszego podstawowego
twierdzenia matematyki finansowej (tw. 4.2)
wynika, że istnieje miara martyngałowa
. Z pierwszego podstawowego
twierdzenia matematyki finansowej (tw. 4.2)
wynika, że istnieje miara martyngałowa ![]() dla rynku rozszerzonego,
a mianowicie taka miara probabilistyczna
dla rynku rozszerzonego,
a mianowicie taka miara probabilistyczna ![]() , że
, że ![]() jest
jest
![]() -martyngałem dla
-martyngałem dla ![]() , czyli
, czyli
Stąd wynika w szczególności, że ![]() oraz
oraz
![]() . Zatem
. Zatem ![]() .
.
Teraz udowodnimy inkluzję odwrotną. Niech ![]() dla pewnego
dla pewnego ![]() . Definiujemy proces
. Definiujemy proces
![]() wzorem
wzorem ![]() . Na
mocy definicji
. Na
mocy definicji ![]() ,
, ![]() oraz proces
oraz proces ![]() jest
jest ![]() -martyngałem, więc rynek rozszerzony o instrument
o cenie
-martyngałem, więc rynek rozszerzony o instrument
o cenie ![]() jest rynkiem bez możliwości arbitrażu. Stąd
jest rynkiem bez możliwości arbitrażu. Stąd ![]() .
.
Z tego twierdzenia wynika, że
Wniosek 6.2
Jeśli ![]() jest rynkiem bez możliwości arbitrażu,
jest rynkiem bez możliwości arbitrażu, ![]() jest
wypłatą osiągalną, to
jest
wypłatą osiągalną, to ![]() jest zbiorem jednoelementowym i
jest zbiorem jednoelementowym i
Zatem dla wypłaty osiągalnej jej cena otrzymana z def. 6.2 jest równa cenie arbitrażowej, co uzasadnia nazywanie ceny z def. 6.2 uogólnioną ceną arbitrażową.
Uwaga 6.1
Zachodzą równości:
Zbiór ![]() jest pusty (gdy na rynku jest arbitraż) lub jest odcinkiem,
gdyż zbiór miar martyngałowych
jest pusty (gdy na rynku jest arbitraż) lub jest odcinkiem,
gdyż zbiór miar martyngałowych ![]() jest zbiorem
wypukłym. Można udowodnić, że gdy rynek jest wolny od arbitrażu, ale
nie jest zupełny, to jest to przedział otwarty.
Odcinek o końcach
jest zbiorem
wypukłym. Można udowodnić, że gdy rynek jest wolny od arbitrażu, ale
nie jest zupełny, to jest to przedział otwarty.
Odcinek o końcach ![]() i
i ![]() nazywamy przedziałem
braku arbitrażu.
Przedział
nazywamy przedziałem
braku arbitrażu.
Przedział ![]() jest przedziałem cen
akceptowanych przez obie strony kontraktu. Stąd potencjalny zysk
(gdyż ceny są losowe) jest traktowany jako wynagrodzenie za zgodę na
ryzyko.
Z rozważań przeprowadzonych w tym paragrafie wiemy, że cena
akceptowana przez obie strony kontraktu należy do przedziału
jest przedziałem cen
akceptowanych przez obie strony kontraktu. Stąd potencjalny zysk
(gdyż ceny są losowe) jest traktowany jako wynagrodzenie za zgodę na
ryzyko.
Z rozważań przeprowadzonych w tym paragrafie wiemy, że cena
akceptowana przez obie strony kontraktu należy do przedziału
![]() . Celem dalszych badań, których nie
będziemy tu opisywać, jest znalezienie najlepszej ceny z tego
przedziału, czyli należy znaleźć miarę martyngałową
. Celem dalszych badań, których nie
będziemy tu opisywać, jest znalezienie najlepszej ceny z tego
przedziału, czyli należy znaleźć miarę martyngałową ![]() , zwaną miarą
wyceniającą, dającą cenę za pomocą wzoru
, zwaną miarą
wyceniającą, dającą cenę za pomocą wzoru ![]() . Są
różne metody wyboru takiej miary martyngałowej
. Są
różne metody wyboru takiej miary martyngałowej ![]() . Zależą one od
subiektywnie przyjętych kryteriów.
. Zależą one od
subiektywnie przyjętych kryteriów.
6.3. Zagadnienia i zadania na ćwiczenia
Ćwiczenie 6.1
Udowodnić lemat 6.1.
Ćwiczenie 6.2
Udowodnić tw. 6.1.
a) ![]() Niech
Niech ![]() replikuje
replikuje ![]() , tj.
, tj.
![]() , stąd
, stąd
Pokażemy, że zachodzi równość. Warunek ![]() pociąga za sobą istnienie strategii
pociąga za sobą istnienie strategii ![]() takiej, że
takiej, że
Ale wtedy portfel ![]() jest arbitrażem, gdyż
jest arbitrażem, gdyż
![]() i
i ![]() .
.
b) ![]() . Niech portfel
. Niech portfel ![]() replikuje
replikuje ![]() .
Wtedy
.
Wtedy ![]() , więc z (6.5)
, więc z (6.5)
Gdyby ![]() , to istniałoby
, to istniałoby ![]() takie, że
takie, że
Ale wtedy portfel ![]() jest arbitrażem, bo
jest arbitrażem, bo
![]() oraz
oraz
Ćwiczenie 6.4
a) Podać przykład strategii dającej zysk bez ryzyka,
gdy kontrakt ![]() został sprzedany za cenę
został sprzedany za cenę ![]() .
.
b) Załóżmy, że kupujący nabył wypłatę ![]() za cenę
za cenę ![]() .
Jak powinien postępować, by osiągnąć zysk bez ryzyka?
.
Jak powinien postępować, by osiągnąć zysk bez ryzyka?
Ponieważ ![]() , więc istnieje portfel
, więc istnieje portfel ![]() ,
taki że
,
taki że ![]() ,
, ![]() oraz
oraz ![]() . Sprzedawca kontraktu konstruuje za kwotę
. Sprzedawca kontraktu konstruuje za kwotę ![]() portfel
portfel
![]() i ze sprzedaży kontraktu i nabycia portfela
i ze sprzedaży kontraktu i nabycia portfela ![]() ma
dodatni zysk w chwili
ma
dodatni zysk w chwili ![]() :
:
Ćwiczenie 6.5
Znaleźć przykład wypłat ![]() i
i ![]() , takich że
, takich że
a)
b)
Rozpatrzmy rynek z przykł. 4.2. Niech ![]() ,
,
![]() . Wtedy
. Wtedy
Ćwiczenie 6.6
Rozpatrzmy rynek jednookresowy z trzema możliwymi zdarzeniami losowymi. Inwestor uważa, że są one jednakowo prawdopodobne. Na rynku stopa procentowa bez ryzyka wynosi 5% i jest jedna akcja mająca proces cen postaci:
Wycenić wypłaty:
Wypłata ![]() jest osiągalna i
jest osiągalna i ![]() . Wypłaty
. Wypłaty
![]() nie są osiągalne. Znajdujemy ogólną postać miary
martyngałowej
nie są osiągalne. Znajdujemy ogólną postać miary
martyngałowej ![]() :
:
Zatem ![]() ,
, ![]() , a stąd
, a stąd ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.




