Zagadnienia

7.1 Opcje amerykańskie, wycena, zabezpieczenie
7.2 Porównanie opcji amerykańskich i europejskich
7.3 Zagadnienia i zadania na ćwiczenia

7. Opcje amerykańskie

Dotąd rozpatrywane wypłaty (opcje typu europejskiego) były typu statycznego, czyli wypłata z opcji następuje w ustalonej chwili $T$ . Teraz rozszerzymy pojęcie instrumentu pochodnego na opcje amerykańskie, czyli na instrument dający posiadaczowi prawo realizacji w dowolnej chwili $0,1,\dots,T$ .

7.1. Opcje amerykańskie, wycena, zabezpieczenie

Definicja 7.1

Opcją amerykańską o terminie wygaśnięcia $T$ nazywamy ciąg adaptowanych nieujemnych zmiennych losowych $Z_{t}$ ,
$t\in{\cal T}=\{ 0,1,\dots,T\}$ .

Zmienną losową $Z_{t}$ interpretujemy jako wypłatę otrzymaną z realizacji opcji amerykańskiej w chwili $t$ , a ponieważ $Z_{t}$ jest ${\cal F}_{t}$ -mierzalne, to wypłata zależy od wiedzy w chwili $t$ .

Przykład 7.1

Amerykańska opcja kupna na akcję o cenie $S$ z ceną wykonania $K$ (dodatnia stała) zadana jest przez $Z_{t}=(S_{t}-K)^{+}$ , $t\in{\cal T}$ . Kupujący otrzymuje prawo do zakupu akcji po cenie $K$ w dowolnej chwili $0,1,\dots,T$ . Analogicznie ciąg $Z_{t}=(K-S_{t})^{+}$ , $t\in{\cal T}$ , zadaje amerykańską opcję sprzedaży na akcje o cenie $S$ z ceną wykonania $K$ .

Posiadacz opcji amerykańskiej ma prawo wykonać ją w dowolnej chwili. Ponieważ posiadacz opcji decyduje czy chwila jej wykonania właśnie nastąpiła i decyduje na podstawie wiedzy zebranej do tego momentu, więc $\{\tau=t\}\in{\cal F}_{t}$ , a więc moment wykonania opcji $\tau$ jest momentem stopu. Sprzedawca opcji dostając za nią zapłatę $U_{0}$ musi postępować w taki sposób, aby w każdej chwili wartość jego portfela $\varphi$ o kapitale początkowym $U_{0}$ przewyższała jego zobowiązania wobec kupca opcji, czyli strategia $\varphi$ musi być taka, by dla wszystkich $t$ zachodziło:

$V_{t}(\varphi)\geq Z_{t}.$

(7.1)

Strategię $\varphi$ spełniająca (7.1) nazywamy strategią zabezpieczającą opcję amerykańską $(Z_{t})_{{t\in{\cal T}}}$ . Zbiór wszystkich takich strategii będziemy oznaczali przez $\Gamma((Z_{t})_{{t\in{\cal T}}}).$ Z warunku (7.1) wynika, że

$V_{{\tau}}(\varphi)\geq Z_{\tau}$

dla dowolnego momentu stopu $\tau$ o wartościach w zbiorze ${\cal T}$ . Korzystając z analogicznych argumentów jak przy definiowaniu ceny sprzedającego przyjmujemy:

Definicja 7.2

Wielkość

$\Pi _{0}^{{a}}((Z_{t})_{{t\in{\cal T}}})=\inf\{ V_{0}(\varphi):\varphi\in\Gamma((Z_{t})_{{t\in{\cal T}}})\}$

(7.2)

nazywamy ceną arbitrażową w chwili $0$ opcji amerykańskiej zadanej przez ciąg wypłat $(Z_{t})_{{t\in{\cal T}}}$ .

Naszym celem będzie teraz znalezienie ceny $\Pi _{0}^{a}((Z_{t})_{{t\in{\cal T}}}).$ Załóżmy, że rozpatrywany rynek jest skończony, bez możliwości arbitrażu i zupeły z jednym instrumentem ryzykownym, czyli ${\cal M}=(B,S,\Phi)$ . Przez $U_{t}$ będziemy oznaczać cenę opcji amerykańskiej w chwili $t$ . Zatem naszym zadaniem jest znalezienie $U_{0}=\Pi _{0}^{{a}}((Z_{t})_{{t\in{\cal T}}})$ . W tym celu skorzystamy z tego, że w chwili $T$ zachodzi $U_{T}=Z_{T}$ i wykorzystamy indukcję wsteczną. W chwili $T-1$ wystawca opcji musi mieć taki kapitał, by zabezpieczyć jedną z wypłat: wypłatę $Z_{{T-1}}$ w chwili $T-1$ albo wypłatę $Z_{T}$ w chwili $T$ , gdyż każdą z nich może wybrać nabywca opcji. Ponieważ rynek jest zupełny, więc wypłata $Z_{T}$ w chwili $T$ jest osiągalna i w chwili $T-1$ jej cena jest równa $B_{{T-1}}E_{{P^{*}}}(\frac{Z_{T}}{B_{{T}}}|{\cal F}_{{T-1}})$ — tyle trzeba mieć w chwili $T-1$ , by zabezpieczyć wypłatę $Z_{T}$ w chwili $T$ . Stąd cena opcji amerykańskiej w chwili $T-1$ wynosi:

$U_{{T-1}}=\max(Z_{{T-1}},B_{{T-1}}E_{{P^{*}}}(Z_{T}^{*}|{\cal F}_{{T-1}})).$

Analogiczne rozumowanie daje cenę opcji amerykańskiej w chwili $t$ :

$U_{{t-1}}=\max\Big(Z_{{t-1}},B_{{t-1}}E_{{P^{*}}}\Big(\frac{U_{{t}}}{B_{t}}\Big|{\cal F}_{{t-1}}\Big)\Big)$

(7.3)

dla $t=1,2,\dots,T$ , gdyż wystawca musi zabezpieczyć jedną z wypłat: natychmiastową w chwili $t-1$ , tj. wypłatę $Z_{{t-1}}$ lub wypłatę w chwili późniejszej, a ona w chwili $t$ jest warta $U_{t}$ . Dzieląc obie strony przez $B_{{t-1}}$ i oznaczając $U_{t}^{*}=\frac{U_{t}}{B_{t}}$ mamy

$U_{{t-1}}^{*}=\max(Z_{{t-1}}^{*},E_{{P^{*}}}(U_{t}^{*}|{\cal F}_{{t-1}})).$

(7.4)

Zatem otrzymaliśmy

Twierdzenie 7.1

Zdyskontowana cena $U^{*}_{T}$ opcji amerykańskiej zadanej przez ciąg wypłat $(Z_{t})_{{t\in{\cal T}}}$ jest $P^{*}$ -nadmartyngałem zadanym wzorem (7.4).

Ze wzoru (7.4) wynika, że ciąg $(U_{t}^{*})_{{t\in{\cal T}}}$ jest obwiednią Snella ciągu $(Z_{t}^{*})_{{t\in{\cal T}}}$ , czyli że $U_{t}^{*}$ jest najmniejszym $P^{*}$ -nadmartyngałem dominującym ciąg $Z_{t}^{*}$ . Stąd wykorzystując elementy teorii optymalnego stopowania mamy

Twierdzenie 7.2

a) 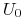$U_{0}$ — cena w chwili 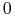$0$ opcji amerykańskiej spełnia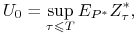

$U_{0}=\sup _{{\tau\leq T}}E_{{P^{*}}}Z_{{\tau}}^{*},$ (7.5)

gdzie 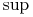$\sup$ bierzemy po momentach stopu 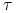$\tau$ o wartościach mniejszych lub równych $T$ .
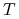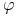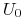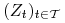b) Istnieje strategia samofinansująca się $\varphi$ o kapitale początkowym $U_{0}$ zabezpieczająca wypłatę z opcji amerykańskiej $(Z_{t})_{{t\in{\cal T}}}$ .
c) Moment stopu

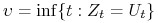
$\upsilon=\inf\{ t:Z_{t}=U_{t}\}$ (7.6)

jest momentem realizacji opcji.

Punkt a). Zdyskontowany proces ceny opcji amerykańskiej $U^{*}$ jest obwiednią Snella ciągu zdyskontowanych wypłat $Z^{*}$ , a stąd korzystając z teorii optymalnego stopowania wynika (7.5).

Punkt b). Jak wiemy, $U_{t}^{*}$ jest $P^{*}$ –nadmartyngałem, więc z tw. Dooba-Meyera o rozkładzie nadmartyngału

$U_{t}^{*}=M_{t}-A_{t},$

(7.7)

gdzie $M$ jest martyngałem, $A$ — procesem rosnącym prognozowalnym, $A_{0}=0$ . Rynek jest zupełny, więc istnieje strategia $\varphi$ taka, że $V_{{T}}^{*}(\varphi)=M_{T}$ . Ponieważ $(V_{t}^{*}(\varphi))_{t}$ jest martyngałem, więc

$V_{t}^{*}(\varphi)=E_{{P^{*}}}(V_{{T}}^{*}(\varphi)|{\cal F}_{t})=E_{{P^{*}}}(M_{T}|{\cal F}_{t})=M_{t}.$

Stąd i z (7.7) mamy $U_{0}=M_{0}=V_{0}(\varphi)$ , czyli $U_{0}$ jest kapitałem początkowym strategii $\varphi$ . Ponadto $U_{t}^{*}=V_{t}^{*}(\varphi)-A_{t},$ czyli

$U_{t}=V_{t}(\varphi)-B_{t}A_{t},$

(7.8)

a ponieważ $B_{t}A_{t}\geq 0$ , proces $U$ dominuje $Z$ , więc

$V_{t}(\varphi)\geq U_{t}\geq Z_{t},$

czyli $\varphi$ zabezpiecza opcję amerykańską.

Punkt c). Mając opcję nie ma sensu realizować jej w chwili $t$ takiej, że $U_{t}>Z_{t}$ , bo sprzedajemy walor wart $U_{t}$ za cenę $Z_{t}$ (lepiej opcję sprzedać za $U_{t}$ niż ją zrealizować i otrzymać $Z_{t}$ ). Stąd moment realizacji opcji (moment stopu) $\tau$ spełnia

$U_{\tau}=Z_{\tau}$

gdyż wiemy, że $U_{t}\geq Z_{t}$ . Nie ma sensu realizować opcji po chwili

$\nu _{{max}}=\inf\{ j:A_{{j+1}}\not=0\}\wedge T=\inf\{ j:A_{{j+1}}^{*}\not=0\}\wedge T,$

gdyż sprzedając opcję w chwili $\nu _{{max}}$ i kupując strategię zabezpieczającą $\varphi$ otrzymamy

$U_{{\nu _{{max}}}}=V_{{\nu _{{max}}}}(\varphi)$

i od tego momentu postępując zgodnie ze strategią $\varphi$ mamy portfel, którego bogactwo jest większe niż wartość opcji w chwili $\nu _{{max}}+1,\dots,T$ . Istotnie, ponieważ (7.8) implikuje

$V_{t}(\varphi)=U_{t}+B_{t}A_{t}$

oraz $A_{t}B_{t}>0$ dla $t>\nu _{{max}}$ , więc $V_{t}(\varphi)>U_{t}$ dla $t=\nu _{{max}}+1,\dots,T$ . Zatem $\tau\leq\nu _{{max}}$ . Pozwala to stwierdzić, że $U^{{*\tau}}$ jest martyngałem, gdyż wtedy $A_{{\tau\wedge t}}=0$ (bo $\tau\wedge t\leq\nu _{{max}}$ ) i korzystamy z przedstawienia (7.7). Stąd wynika, że dla nabywcy opcji najlepszym momentem realizacji opcji jest optymalny moment stopu dla ciągu $(Z_{t}^{*})$ przy rozkładzie prawdopodobieństwa $P^{*}$ (korzystamy z tw. charakteryzującego moment optymalny). A jak wiadomo moment stopu zdefiniowany wzorem (7.6) ma taką własność.

∎

Uwaga 7.1

a) Z tw. 7.2 mamy, że

$\Pi _{0}^{{a}}((Z_{t})_{{t\in{\cal T}}})=\sup _{{\tau}}E_{{P^{*}}}Z_{{\tau}}^{*},$

czyli cena zdefiniowana wzorem (7.2) satysfakcjonuje także kupującego. Kupujący chce najlepiej wykorzystać swoje prawa i uzyskać jak największą wypłatę. Gdy kupujący realizuje opcję w momencie stopu $\tau$ i otrzymuje wypłatę $Z_{\tau}$ , to jest skłonny zapłacić za tę wypłatę $E_{{P^{*}}}Z_{{\tau}}^{*}$ . A ponieważ kupujący może zrealizować opcję w każdym momencie, więc za uczciwą cenę uważa $\sup _{{\tau}}E_{{P^{*}}}Z_{{\tau}}^{*}$ , gdzie supremum bierzemy po momentach stopu $\tau$ o wartościach mniejszych lub równych $T$ .

b) Punkt c) twierdzenia odpowiada na zasadnicze pytanie z punktu widzenia nabywcy: kiedy należy zrealizować opcję. Z dowodu tego punktu wynika, że moment wykonania opcji należy wybrać jako optymalny moment stopu dla problemu optymalnego stopowania ciągu $Z_{t}^{*}$ . Taki moment nie jest wyznaczony jednoznacznie. Jednym z takich momentów jest moment zdefiniowany wzorem (7.6). Wybieramy go, gdyż (7.6), daje jego jawną postać. Mamy regułę jak ten moment wyznacznaczyć praktycznie.

Wykorzystując dowód punktu c) twierdzenia możemy zanalizować sytuacje wystawcy opcji. Wystawca opcji stosuje strategię $\varphi$ i czeka na to, co zrobi nabywca. Jeżeli nabywca zrealizuje opcję w chwili optymalnej $\tau$ , to $U_{\tau}=Z_{\tau}=V_{\tau}(\varphi)$ . Wtedy sprzedawca stosując strategię $\varphi$ otrzymuje całą kwotę, którą musi wypłacić nabywcy opcji. Sprzedawca zabezpieczył swoje zobowiązanie wobec nabywcy. Jeśli natomiast nabywca zrealizuje opcję w innej chwili $\sigma$ niż optymalna $\tau$ , to wystawca ma dodatni zysk. Istotnie, gdy moment realizacji $\sigma$ nie jest optymalny, to $U_{{\sigma}}>Z_{{\sigma}}$ lub $A_{{\sigma}}>0$ i korzystając z (7.8) otrzymujemy zysk wystawcy:

$V_{{\sigma}}(\varphi)-Z_{{\sigma}}=A_{{\sigma}}B_{{\sigma}}+U_{{\sigma}}-Z_{{\sigma}}>0.$

7.2. Porównanie opcji amerykańskich i europejskich

Zajmiemy się teraz porównaniem opcji amerykańskich i europejskich. Opcje amerykańskie dają posiadaczowi więcej praw niż europejskie, więc powinny kosztować więcej.

Twierdzenie 7.3

Niech $U_{t}$ będzie wartością w chwili $t$ opcji amerykańskiej zadanej przez ciąg $(Z_{t})_{t}$ , a $C_{t}$ wartością w chwili $t$ opcji europejskiej o wypłacie $X=Z_{T}$ . Wtedy

$U_{t}\geq C_{t}.$

(7.9)

Ponadto, gdy dla każdego $t\leq T$ mamy

$C_{t}\geq Z_{t},$

(7.10)

to dla każdego $t\leq T$ mamy

$U_{t}=C_{t}.$

(7.11)

Ponieważ $U_{t}^{*}$ jest $P^{*}$ -nadmartyngałem oraz $U_{T}=Z_{T}=X=C_{T}$ , więc

$U_{t}^{*}\geq E_{{P^{*}}}({U_{T}^{*}}|{{\cal F}_{t}})=E_{{P^{*}}}({C_{T}^{*}}|{{\cal F}_{t}})=C_{t}^{*}.$

Stąd $U_{t}\geq C_{t}$ , czyli zachodzi warunek (7.9). Z warunku (7.10) wynika, że $C_{t}^{*}\geq Z_{t}^{*}$ , a ponieważ $C_{t}^{*}$ jest $P^{*}$ -martyngałem, w szczególności $P^{*}$ -nadmartyngałem, więc

$C_{t}^{*}\geq U_{t}^{*},$

(7.12)

bowiem $U_{t}^{*}$ jest najmniejszym nadmartyngałem dominującym $(Z_{t}^{*})_{t}$ . Teraz (7.9) i (7.12) dają (7.11).

∎

Z tw. 7.3 wynika, że amerykańska opcja kupna jest warta tyle samo, co europejska..

Wniosek 7.1

Ceny amerykańskiej i europejskiej opcji kupna z tym samym terminem wygaśnięcia i tę samą cena wykonania są równe.

Wypłaty to $Z_{t}=(S_{t}-K)^{+}$ i $X=C_{T}=Z_{T}$ . Ponieważ $x^{+}\geq x$ i $r\geq 0$ , więc

	$\displaystyle C_{t}$	$\displaystyle=$	$\displaystyle B_{t}E_{{P^{}}}(B_{T}^{{-1}}(S_{T}-K)^{+}\|{\cal F}_{t})\geq B_{t}E_{{P^{}}}(B_{T}^{{-1}}S_{T}-B_{T}^{{-1}}K\|{\cal F}_{t})=$
		$\displaystyle=$	$\displaystyle S_{t}-KB_{t}B_{T}^{{-1}}\geq S_{t}-K.$

Stąd

$C_{t}\geq(S_{t}-K)^{+}=Z_{t},$

gdyż $C_{t}\geq 0$ . Otrzymaliśmy (7.10) i twierdzenie 7.3 daje tezę.

∎

Ogólniejszą wersję wniosku można znaleźć w ćw. 7.5.

Przykład 7.2

Na rynku zupełnym opisanym w przykł. 4.2 chcemy znaleźć ceny amerykańskiej opcji kupna i amerykańskiej opcji sprzedaży z ceną wykonania $K=105$ , a także znaleźć optymalny momentem wykonania opcji sprzedaży przez nabywcę opcji.

Jak wiemy, cena amerykańskiej opcji kupna jest równa cenie opcji europejskiej (tw. 7.3), więc korzystając z przykł. 4.2 otrzymujemy $C^{a}_{0}=17{,}36$ . Obliczymy cenę amerykańskiej opcji sprzedaży. Korzystamy ze wzoru (7.3) kolejno dla $t=2$ i $t=1$ , otrzymując:

$\displaystyle U_{2}$	$\displaystyle=$	$\displaystyle(105-S_{2})^{+},$
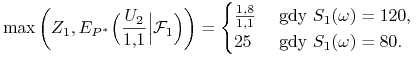$\displaystyle U_{{1}}$	$\displaystyle=$	$\displaystyle\max\left(Z_{{1}},E_{{P^{*}}}\Big(\frac{U_{{2}}}{1{,}1}\Big\|{\cal F}_{{1}}\Big)\right)=\begin{cases}\frac{1{,}8}{1{,}1}&\text{ gdy }S_{1}(\omega)=120,\cr 25&\text{ gdy }S_{1}(\omega)=80.\end{cases}$
$\displaystyle U_{0}$	$\displaystyle=$	$\displaystyle\max(5,E_{{P^{*}}}(\frac{U_{{1}}}{1{,}1}\Big\|{\cal F}_{0}))=\max(5;6{,}30)=6{,}30.$

Moment stopu zdefiniowany wzorem

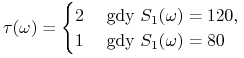$\tau(\omega)=\begin{cases}2&\text{ gdy }S_{1}(\omega)=120,\cr 1&\text{ gdy }S_{1}(\omega)=80\end{cases}$

jest optymalnym momentem wykonania opcji sprzedaży przez jej posiadacza.

7.3. Zagadnienia i zadania na ćwiczenia

Ćwiczenie 7.1

Bank ma amerykańską opcję sprzedaży akcji z ceną realizacji 60 i datą wygaśnięcia za $3/4$ roku. Walor (akcja) wart jest teraz 6, a stopa procentowa bez ryzyka (kapitalizacja ciągła) wynosi $18\%$ p.a.¹skrót łac. per annum, w skali roku. Czy warto opcję zrealizować teraz, czy w chwili wygaśnięcia?

Rozwiązanie:

Teraz mamy $60-6=54$ , wkładamy do banku i za $3/4$ roku mamy $54\cdot e^{{0{,}18\cdot\frac{3}{4}}}=61{,}81$ . W chwili wygaśnięcia opcja jest warta co najwyżej 60 (gdy $S_{T}=0$ ). Zatem warto opcję zrealizować teraz. Wynika to z faktu, że cena waloru jest niska w porównaniu z ceną wykonania opcji. W takim przypadku wykonujemy opcję i inwestujemy otrzymane pieniądze.

Ćwiczenie 7.2

Mówimy, że opcja amerykańska $(Z_{t})_{{t\in{\cal T}}}$ jest zawsze realizowalna, gdy dla dowolnego momentu stopu $\tau$ o wartościach mniejszych lub równych $T$ istnieje strategia $\varphi\in\Phi$ taka, że

$V_{{\tau}}(\varphi)=Z_{{\tau}}.$

Udowodnić, że na rynku zupełnym każda opcja amerykańska jest zawsze realizowalna.

Rozwiązanie:

Ustalmy dowolny moment stopu $\tau$ . Na mocy zupełności rynku wypłata

$X=\frac{Z_{{\tau}}}{B_{{\tau}}}B_{{T}}$

jest osiągalna, więc istnieje $\varphi\in\Phi$ takie, że $V_{T}(\varphi)=X$ . Stąd

$V_{t}^{*}(\varphi)=E_{{P^{*}}}\Big(\frac{X}{B_{T}}\Big|{\cal F}_{t}\Big)=E_{{P^{*}}}\Big(\frac{Z_{{\tau}}}{B_{{\tau}}}\Big|{\cal F}_{t}),$

a więc

$V_{{\tau}}^{*}(\varphi)=E_{{P^{*}}}\Big(\frac{Z_{{\tau}}}{B_{{\tau}}}\Big|{\cal F}_{{\tau}}\Big)=\frac{Z_{{\tau}}}{B_{{\tau}}},$

czyli $V_{{\tau}}(\varphi)=Z_{{\tau}}$ .

Ćwiczenie 7.3

Udowodnić, że gdy na rynku zupełnym opcja amerykańska jest wyceniana wzorem (7.5), to

a) nie istnieje arbitraż związany z pozycją krótką (tj. wystawcy opcji),

b) nie istnieje arbitraż związany z pozycją długą (tj. nabywcy opcji).

Rozwiązanie:

a) Nie wprost. Gdyby istniał arbitraż związany z pozycją krótką, to sprzedawca posługiwałby się portfelem $\varphi$ zabezpieczającym opcję amerykańską takim, że dla każdego momentu wykonania opcji przez kupującego, tj. momentu stopu $\tau$ , ma on zysk bez ryzyka:

$V_{\tau}(\varphi)\geq Z_{\tau},\quad P(V_{\tau}(\varphi)>Z_{\tau})>0.$

Wtedy

$V_{0}(\varphi)=E_{{P^{*}}}V^{*}_{\tau}(\varphi)>E_{{P^{*}}}Z^{*}_{\tau}$

dla każdego momentu stopu $\tau$ , co na mocy skończoności $\Omega$ implikuje

$V_{0}(\varphi)>\sup _{\tau}E_{{P^{*}}}Z^{*}_{\tau}=U_{0},$

sprzeczność.

Ćwiczenie 7.4

Niech w modelu CRR: $S_{0}=100;S_{1}^{d}=80;$ $S_{1}^{u}=130;T=3;$ $r=0{,}1$ . Znaleźć cenę w chwili 0 opcji amerykańskiej o wypłacie $Z_{t}=\max _{{\{ 0\leq u~\leq t\}}}S_{u}$ (jest tzw. opcja rosyjska. Znaleźć moment wykonania opcji. Znaleźć dla niej strategię zabezpieczającą.

Rozwiązanie:

Z danych wynika, że rynek jest wolny od arbitrażu. Miara martyngałowa $P^{*}$ jest wyznaczona przez $p=0{,}6$ .
Znajdujemy wartość wypłaty $X=f(S_{0},S_{1},S_{2},S_{3})$ dla każdej ścieżki, a następnie obliczamy cenę: $\Pi _{0}(X)=104{,}58$ . $\Pi^{a}_{0}((Z_{t})_{t})=116{,}09$ . Moment

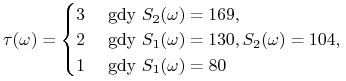$\tau(\omega)=\begin{cases}3&\text{ gdy }S_{2}(\omega)=169,\cr 2&\text{ gdy }S_{1}(\omega)=130,S_{2}(\omega)=104,\cr 1&\text{ gdy }S_{1}(\omega)=80\end{cases}$

jest optymalnym momentem wykonania opcji przez posiadacza. Strategię zabezpieczającą znajdujemy korzystając np. z tw. 7.2 i postaci martyngału w rozkładzie Dooba

Ćwiczenie 7.5

Niech ciąg $\big(g(S_{t})\big)_{t}$ , gdzie $g$ jest funkcją wypukłą, nieujemną, $g(0)=0$ , zadaje opcję amerykańską na rynku zupełnym. Udowodnić, że cena tej opcji amerykańskiej jest równa cenie opcji europejskiej o wypłacie $X=g(S_{T})$ .

Rozwiązanie:

Ponieważ $g(0)=0$ , więc z wypukłości funkcji $g$ otrzymujemy

$g(ax)\leq ag(x),\quad x\geq 0,a\in[0,1].$

Stąd i z nierówności Jensena

$g(S_{t})\leq E_{{P^{*}}}\Big(g\Big(\frac{S_{{t+1}}}{1+r}\Big)\Big|{\cal F}_{t}\Big)\leq E_{{P^{*}}}\Big(\frac{g(S_{{t+1}})}{1+r})\Big|{\cal F}_{t}\Big).$

Zatem $\frac{g(S_{{t}})}{(1+r)^{t}}$ jest podmartyngałem i

$Z_{t}=g(S_{t})\leq(1+r)^{{t-T}}E_{{P^{*}}}(g(S_{T})|{\cal F}_{t})=\Pi _{t}(X).$

Otrzymaliśmy (7.10) i tw. 7.3 daje tezę.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Modele matematyczne rynków instrumentów pochodnych I

Zagadnienia

7. Opcje amerykańskie

7.1. Opcje amerykańskie, wycena, zabezpieczenie

Definicja 7.1

Przykład 7.1

Definicja 7.2

Twierdzenie 7.1

Twierdzenie 7.2

Uwaga 7.1

7.2. Porównanie opcji amerykańskich i europejskich

Twierdzenie 7.3

Wniosek 7.1

Przykład 7.2

7.3. Zagadnienia i zadania na ćwiczenia

Ćwiczenie 7.1

Ćwiczenie 7.2

Ćwiczenie 7.3

Ćwiczenie 7.4

Ćwiczenie 7.5