Zagadnienia
8. Rynek kontraktów terminowych futures
8.1. Opis kontraktów terminowych futures
Kontrakt terminowy futures jest to instrument finansowy
zobowiązujący obie strony kontraktu do realizacji w przyszłości
transakcji na określonych w nim warunkach. W chwili zawierania
kontrakt futures nic nie kosztuje, zatem jest wart ![]() . Kontraktami
terminowymi futures (w przeciwieństwie do forward) handluje się na
giełdzie. Obie strony kontraktu nie znają się wzajemnie, gdyż
kontrakt zawarły poprzez pośrednika — giełdę. Kontrakty futures
odznaczają się następującymi cechami:
. Kontraktami
terminowymi futures (w przeciwieństwie do forward) handluje się na
giełdzie. Obie strony kontraktu nie znają się wzajemnie, gdyż
kontrakt zawarły poprzez pośrednika — giełdę. Kontrakty futures
odznaczają się następującymi cechami:
-
kontrakty są standaryzowane, czyli są ściśle określone wszystkie warunki kontraktu, w tym nominalna wielkość przedmiotu kontraktu futures i termin dostawy,
-
cena futures jest ustalana na giełdzie,
-
w każdej chwili można kontrakt futures zamknąć wchodząc w pozycję przeciwną,
-
kontrakt jest rozliczany codziennie za pomocą procedury dziennej aktualizacji depozytu (marking-to-market).
Kontrakty tego rodzaju obarczone są ryzykiem związanym ze zmianami cen, ale zostało wyeliminowane ryzyko związane z niewywiązaniem się jednej ze stron z warunków umowy. Na różnych rynkach istnieją różne kontrakty futures, m.in. kontrakty futures na akcje — instrument bazowy stanowią akcje, kontrakty futures walutowe — instrument bazowy stanowi waluta innego kraju, kontrakty futures na indeks giełdowy. Z kontraktem futures związane są ceny:
-
cena futures w dniu zawarcia kontraktu — po takiej cenie zostanie zawarta transakcja w przyszłości,
-
cena kontraktu futures na rynku — cena dzisiejsza tego kontraktu, cena zmieniająca się każdego dnia w okresie notowań,
-
cena bieżąca przedmiotu kontraktu (spot price).
Wejście w kontrakt futures nic nie kosztuje, ale podmiot chcący
uczestniczyć w rynku futures musi wnieść na konto pewien depozyt
zabezpieczający — wadium. Codziennie Izba Rozrachunkowa (clearing house) koryguje stan konta o zmianę cen kontraktu futures
w ciągu dnia. Gdy cena wzrośnie w ciągu dnia o ![]() , to stan rachunku
sprzedającego kontrakt zmaleje o
, to stan rachunku
sprzedającego kontrakt zmaleje o ![]() , a kupującego wzrośnie o
, a kupującego wzrośnie o ![]() .
Obie strony muszą utrzymywać na rachunku pewną ustaloną sumę (maintenance margin level). Gdy wartość rachunku po rozliczeniu
spada poniżej tej wielkości Izba Rozrachunkowa wzywa inwestora do
natychmiastowej dopłaty pieniędzy na rachunek. Gdy wezwanie zostanie
zignorowane następuje zamknięcie kontraktu.
.
Obie strony muszą utrzymywać na rachunku pewną ustaloną sumę (maintenance margin level). Gdy wartość rachunku po rozliczeniu
spada poniżej tej wielkości Izba Rozrachunkowa wzywa inwestora do
natychmiastowej dopłaty pieniędzy na rachunek. Gdy wezwanie zostanie
zignorowane następuje zamknięcie kontraktu.
Intuicyjnie można sobie wyobrażać, że kontrakt futures jest zamykany na końcu dnia handlowego (bo jest rozliczany) i otwierany na nowo następnego dnia, czyli kontrakt futures można traktować jako ciąg jednodniowych kontraktów forward. Taka procedura jednocześnie daje inwestorowi możliwość zamknięcia pozycji w każdej chwili. Inwestor zamyka pozycję wchodząc w kontrakt przeciwny, czyli otwiera pozycję przeciwną do tej, którą zajął wchodząc na rynek futures. Może to zrobić w każdej chwili, zarówno gdy chce zrealizować osiągnięte zyski, jak i wycofać się by zminimalizować straty. Przy okazji warto zaznaczyć, że bardzo mało kontraktów (niektóre źródła podają, że mniej niż 2%) jest w istocie rozliczanych w momencie wygaśnięcia, czyli dla większości uczestników dostawa przedmiotu kontraktu futures jest jedynie potencjalna.
8.2. Model rynku
Wykorzystując idee poznane wcześniej skonstruujemy teraz model rynku kontraktów terminowych futures. W związku ze specyfiką kontraktów futures model ten różni się trochę od modelu rynku skończonego, opisywanego do tej pory.
Jak poprzednio, zakładamy, że mamy ustaloną przestrzeń
probabilistyczną ![]() , gdzie
, gdzie ![]() jest zbiorem
skończonym,
jest zbiorem
skończonym, ![]() , a prawdopodobieństwo
, a prawdopodobieństwo ![]() jest
takie, że
jest
takie, że ![]() dla każdego
dla każdego ![]() . Transakcje na
rynku odbywają się w chwilach
. Transakcje na
rynku odbywają się w chwilach ![]() ,
, ![]() i mamy
daną filtrację
i mamy
daną filtrację ![]() ,
, ![]() opisującą
wiedzę o rynku (
opisującą
wiedzę o rynku (![]() -ciało
-ciało ![]() opisuje wiedzę do
chwili
opisuje wiedzę do
chwili ![]() ), taką że
), taką że ![]() .
Niech
.
Niech ![]() oznacza proces cen futures na instrument bazowy
o cenie
oznacza proces cen futures na instrument bazowy
o cenie ![]() z momentem wykonania
z momentem wykonania ![]() . Wielkość
. Wielkość ![]() jest to
cena zapłaty w chwili
jest to
cena zapłaty w chwili ![]() na którą się umawiamy dziś, tj. w chwili
0. Wprowadzimy oznaczenie skracające napisy:
na którą się umawiamy dziś, tj. w chwili
0. Wprowadzimy oznaczenie skracające napisy: ![]() .
.
Na rynku futures inwestor może inwestować w rachunek bankowy i ![]() różnych kontraktów futures z tą samą datą realizacji i adaptowanym
procesem cen
różnych kontraktów futures z tą samą datą realizacji i adaptowanym
procesem cen ![]() ,
, ![]() , gdzie
, gdzie
![]() jest ceną (kursem rozliczeniowym)
jest ceną (kursem rozliczeniowym) ![]() -tego kontraktu futures,
-tego kontraktu futures,
![]() . Jak zawsze, proces
. Jak zawsze, proces ![]() jest wartością jednostki
bankowej. Zakładamy, że kapitalizacja jest okresowa, oprocentowanie
jest stałe i równe w skali jednego okresu
jest wartością jednostki
bankowej. Zakładamy, że kapitalizacja jest okresowa, oprocentowanie
jest stałe i równe w skali jednego okresu ![]() ,
, ![]() .
.
Na tym rynku strategią jest proces
gdzie ![]() jest wielkością kapitału w banku (tj. zmienną
losową adaptowaną), a
jest wielkością kapitału w banku (tj. zmienną
losową adaptowaną), a ![]() jest procesem prognozowalnym mówiącym jakie pozycje zajął inwestor
w kontraktach futures.
jest procesem prognozowalnym mówiącym jakie pozycje zajął inwestor
w kontraktach futures. ![]() jest procesem prognozowalnym,
gdyż inwestor określa w chwili
jest procesem prognozowalnym,
gdyż inwestor określa w chwili ![]() liczbę pozycji zajętych na
rynku futures, które będą w jego portfelu w chwili
liczbę pozycji zajętych na
rynku futures, które będą w jego portfelu w chwili ![]() .
. ![]() jest procesem adaptowanym, gdyż inwestor dopiero po dokonaniu
rozliczenia kontraktów futures zawartych w chwili
jest procesem adaptowanym, gdyż inwestor dopiero po dokonaniu
rozliczenia kontraktów futures zawartych w chwili ![]() wie, ile ma
pieniędzy w chwili
wie, ile ma
pieniędzy w chwili ![]() . Ze względu na specyfikę kontraktu futures
bogactwo portfela odzwierciedla wielkość kapitału posiadanego przez
inwestora, gdyż wejście w kontrakt futures nic nie kosztuje. Zatem
definiujemy:
. Ze względu na specyfikę kontraktu futures
bogactwo portfela odzwierciedla wielkość kapitału posiadanego przez
inwestora, gdyż wejście w kontrakt futures nic nie kosztuje. Zatem
definiujemy:
| (8.1) |
Strategię ![]() nazywamy samofinansującą się, gdy
nazywamy samofinansującą się, gdy
| (8.2) |
tj. wartość portfela w chwili ![]() jest równa wartości w chwili
jest równa wartości w chwili
![]() inwestycji w rachunek bankowy w chwili
inwestycji w rachunek bankowy w chwili ![]() zwiększonej
o rozliczenie pozycji futures (skutek procedury ,,równaj do
rynku”). Przez
zwiększonej
o rozliczenie pozycji futures (skutek procedury ,,równaj do
rynku”). Przez ![]() oznaczać będziemy przestrzeń liniową
strategii samofinansujących się na rynku futures. Proces zysku jest
zadany wzorem:
oznaczać będziemy przestrzeń liniową
strategii samofinansujących się na rynku futures. Proces zysku jest
zadany wzorem:
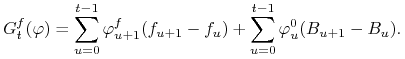 |
Z następnego twierdzenia widać, że definicja portfela samofinansującego się na rynku futures jest naturalna.
Twierdzenie 8.1
Strategia ![]() jest strategią samofinansującą się na rynku
futures wtedy i tylko wtedy, gdy
jest strategią samofinansującą się na rynku
futures wtedy i tylko wtedy, gdy
![]() Z warunków (8.1) i (8.2)
otrzymujemy
Z warunków (8.1) i (8.2)
otrzymujemy
![\displaystyle V_{0}^{f}(\varphi)+\sum _{{u=0}}^{{t-1}}[V_{{u+1}}^{f}(\varphi)-V_{u}^{f}(\varphi)]=](wyklady/ip1/mi/mi1404.png) |
||||
![\displaystyle V_{0}^{f}(\varphi)+\sum _{{u=0}}^{{t-1}}[\varphi _{{u+1}}^{f}(f_{{u+1}}-f_{u})+\varphi _{u}^{0}(B_{{u+1}}-B_{u})]=V_{0}^{f}(\varphi)+G_{t}^{f}(\varphi).](wyklady/ip1/mi/mi1428.png) |
![]() Korzystając z założeń, definicji wartości portfela
(8.1) i definicji procesu zysku
otrzymujemy
Korzystając z założeń, definicji wartości portfela
(8.1) i definicji procesu zysku
otrzymujemy
otrzymujemy zatem warunek (8.2), czyli ![]() jest
strategią samofinansującą się.
jest
strategią samofinansującą się.
Rynek ![]() nazywamy rynkiem bez możliwości arbitrażu gdy klasa strategii
samofinansujących się
nazywamy rynkiem bez możliwości arbitrażu gdy klasa strategii
samofinansujących się ![]() nie zawiera strategii arbitrażowej
tzn. nie istnieje
nie zawiera strategii arbitrażowej
tzn. nie istnieje ![]() , takie że
, takie że
Wypłatą europejską ![]() w chwili
w chwili ![]() nazywamy dowolną
nazywamy dowolną ![]() –mierzalną zmienną losową.
Strategię
–mierzalną zmienną losową.
Strategię ![]() nazywamy strategią
replikującą wypłatę
nazywamy strategią
replikującą wypłatę ![]() gdy
gdy ![]() Wypłatę
Wypłatę ![]() nazywamy osiągalną, gdy istnieje strategia ją replikująca. Jak
poprzednio, wypłatę nazwiemy jednoznacznie replikowalną, gdy dla
dowolnych strategii
nazywamy osiągalną, gdy istnieje strategia ją replikująca. Jak
poprzednio, wypłatę nazwiemy jednoznacznie replikowalną, gdy dla
dowolnych strategii ![]() replikujących
replikujących ![]() mamy
mamy
![]() dla wszystkich
dla wszystkich ![]() . Wtedy proces
. Wtedy proces
![]() nazywamy procesem bogactwa
nazywamy procesem bogactwa ![]() .
Zachodzi twierdzenie o jednoznaczności procesu bogactwa portfela replikującego.
.
Zachodzi twierdzenie o jednoznaczności procesu bogactwa portfela replikującego.
Twierdzenie 8.2
Gdy ![]() jest rynkiem bez możliwości
arbitrażu, to każda wypłata osiągalna jest jednoznacznie
replikowalna.
jest rynkiem bez możliwości
arbitrażu, to każda wypłata osiągalna jest jednoznacznie
replikowalna.
Dowód przebiega analogicznie do dowodu tw.
3.4 i pozostawiamy go jako ćwiczenie dla
Czytelnika. Korzystając z tego twierdzenia definiujemy proces ceny
arbitrażowej ![]() wypłaty osiągalnej
wypłaty osiągalnej ![]() na rynku
na rynku ![]() bez możliwości arbitrażu jako wartość procesu bogactwa, tzn.
bez możliwości arbitrażu jako wartość procesu bogactwa, tzn.
gdzie ![]() jest strategią replikującą
jest strategią replikującą ![]() .
.
Przykład 8.1
Niech na rynku futures jednookresowym dwustanowym ceny pewnego aktywa wynoszą
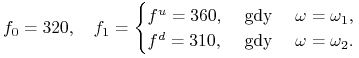 |
Znajdziemy cenę arbitrażową europejskiej opcji kupna wystawionej na
to aktywo na rynku futures, gdy ![]() miesiące,
miesiące, ![]() i stopa
procentowa dla tego okresu wynosi
i stopa
procentowa dla tego okresu wynosi ![]() . Wtedy wypłata z tej opcji
wynosi
. Wtedy wypłata z tej opcji
wynosi
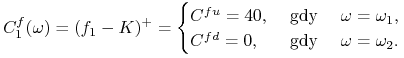 |
Wielkość ![]() — wartość portfela replikującego
— wartość portfela replikującego
![]() musi spełniać
musi spełniać
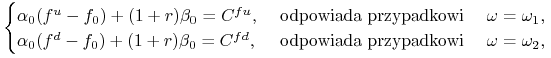 |
zatem
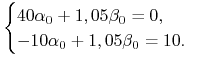 |
Stąd
![]() ,
, ![]() , zatem
cena jest równa
, zatem
cena jest równa
Znajdujmy teraz cenę arbitrażową opcji sprzedaży na rynku futures przy tych samych parametrach. Portfel replikujący spełnia:
Stąd mamy ![]() ,
,
![]() . Cena opcji sprzedaży wynosi
. Cena opcji sprzedaży wynosi
![]() , jest zatem taka sama jak cena opcji kupna, co na
rynku futures — jak się dalej przekonamy — nie jest przypadkiem.
, jest zatem taka sama jak cena opcji kupna, co na
rynku futures — jak się dalej przekonamy — nie jest przypadkiem.
Znajdowanie ceny, gdy korzystamy z samej definicji jest, poza prostymi przykładami jak wyżej, kłopotliwe. Stąd, jak poprzednio, w celu badania rynku i znajdowania procesów cen wypłat wprowadzamy aparat miar martyngałowych.
Definicja 8.1
Miarę probabilistyczną ![]() równoważną z
równoważną z ![]() nazywamy miarą
martyngałową dla rynku futures, gdy proces cen futures
nazywamy miarą
martyngałową dla rynku futures, gdy proces cen futures ![]() jest
jest ![]() -martyngałem.
-martyngałem.
Warto podkreślić, że w tej definicji wykorzystujemy proces cen futures, a nie proces cen futures zdyskontowanych, jak przyjęliśmy w def. 2.6.
Przez ![]() będziemy oznaczać zbiór miar martyngałowych dla
procesu cen futures. Jak poprzednio, wygodnie jest posługiwać się
zdyskontowanym procesem bogactwa portfela
będziemy oznaczać zbiór miar martyngałowych dla
procesu cen futures. Jak poprzednio, wygodnie jest posługiwać się
zdyskontowanym procesem bogactwa portfela ![]() :
:
Lemat 8.1
Strategia ![]() jest strategią samofinansującą się na rynku
futures
jest strategią samofinansującą się na rynku
futures ![]() wtedy i tylko wtedy, gdy dla
każdego
wtedy i tylko wtedy, gdy dla
każdego ![]()
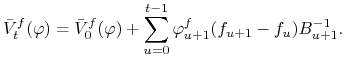 |
(8.3) |
Dowód lematu zostawimy jako zadanie (zad 8.4).
Wniosek 8.1
Jeżeli ![]() , to dla każdego
, to dla każdego
![]() proces
proces ![]() jest
jest
![]() –martyngałem.
–martyngałem.
Stąd wprowadzając ![]() — klasę miar
martyngałowych dla rynku
— klasę miar
martyngałowych dla rynku ![]() jako zbiór tych miar
probabilistycznych
jako zbiór tych miar
probabilistycznych ![]() , dla których
, dla których
![]() jest
jest ![]() -martyngałem dla każdego
-martyngałem dla każdego
![]() , otrzymujemy, że
, otrzymujemy, że
| (8.4) |
Następnie dla rynku futures dowodzi się podstawowe twierdzenia matematyki finansowej. Są one odpowiednikami podstawowych twierdzeń dla rynku akcji, a ich dowody przebiegają w podobny sposób.
Twierdzenie 8.3
Rynek ![]() jest wolny od
arbitrażu wtedy i tylko wtedy, gdy
jest wolny od
arbitrażu wtedy i tylko wtedy, gdy ![]() . Wówczas cena arbitrażowa wypłaty osiągalnej
. Wówczas cena arbitrażowa wypłaty osiągalnej ![]() wynosi
wynosi
| (8.5) |
dla ![]() .
.
Twierdzenie 8.4
Rynek ![]() bez możliwości arbitrażu jest
zupełny wtedy i tylko wtedy, gdy istnieje dokładnie jedna miara
martyngałowa.
bez możliwości arbitrażu jest
zupełny wtedy i tylko wtedy, gdy istnieje dokładnie jedna miara
martyngałowa.
Znajdziemy teraz postać parytetu na rynku futures. Ponieważ
więc ze wzoru (8.5) na cenę futures mamy
| (8.6) |
Jest to wzór dający parytet kupna-sprzedaży dla opcji na rynku futures. Stąd jako wniosek otrzymujemy
więc na rynku futures cena opcji sprzedaży jest równa cenie opcji kupna o tej samej cenie wykonania, gdy cena wykonania jest równa obecnej cenie futures (tak było w przykł. 8.1).
8.3. Zagadnienia i zadania na ćwiczenia
Ćwiczenie 8.1
Udowodnić, że rynek futures jednookresowy dwustanowy jest wolny od arbitrażu wtedy i tylko wtedy, gdy
| (8.7) |
(oznaczenia ![]() jak w przykł. 8.1).
jak w przykł. 8.1).
![]() Nie wprost. Gdy
Nie wprost. Gdy ![]() , to portfel
, to portfel
![]() jest arbitrażem, gdyż
jest arbitrażem, gdyż
(ponieważ ![]() ) i
) i
Gdy ![]() , to portfel
, to portfel ![]() jest arbitrażem.
jest arbitrażem.
![]() Niech
Niech ![]() będzie portfelem takim,
że
będzie portfelem takim,
że ![]() . Wtedy
. Wtedy ![]() . Gdy
. Gdy ![]() , to
, to
![]() i
i ![]() . Gdy
. Gdy ![]() , to
, to
![]() . Stąd korzystając z warunku
(8.7) otrzymujemy, że istnieje
. Stąd korzystając z warunku
(8.7) otrzymujemy, że istnieje ![]() taka, że
taka, że
![]() , czyli nie istnieje arbitraż.
, czyli nie istnieje arbitraż.
Ćwiczenie 8.2
Udowodnić, że
a) Jeśli na rynku futures jednookresowym dwustanowym miara
martyngałowa ![]() istnieje, to jest określona przez równość:
istnieje, to jest określona przez równość:
| (8.8) |
gdzie ![]() . Zatem
. Zatem
| (8.9) |
b) Miara martyngałowa ![]() istnieje wtedy i tylko wtedy, gdy
istnieje wtedy i tylko wtedy, gdy
![]() .
.
Ćwiczenie 8.3
Udowodnić, że gdy ![]() jest rynkiem bez
możliwości arbitrażu, to
jest rynkiem bez
możliwości arbitrażu, to
| (8.10) |
Kontrakt futures wypłaca w chwili ![]() wielkość
wielkość
W chwili 0 ten kontrakt nic nie kosztuje, więc
co daje (8.10).
Ćwiczenie 8.4
Udowodnić lemat 8.1.
Ćwiczenie 8.5
Udowodnić, że ![]() jest przestrzenią liniową.
jest przestrzenią liniową.
Ćwiczenie 8.6
Udowodnić tw. 8.2.
Naśladować dowód dla rynku akcji.
Ćwiczenie 8.7
Udowodnić tw. 8.3.
Ćwiczenie 8.8
Udowodnić tw. 8.4.
Ćwiczenie 8.9
Udowodnić, że ![]() wtedy i tylko wtedy, gdy dla
każdego momentu
wtedy i tylko wtedy, gdy dla
każdego momentu ![]()
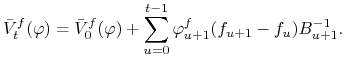 |
Ćwiczenie 8.10
Niech ![]() będzie rynkiem, na którym handlujemy instrumentami
bazowymi i kontraktami futures oraz możemy inwestować w lokaty
bankowe. Udowodnić, że
będzie rynkiem, na którym handlujemy instrumentami
bazowymi i kontraktami futures oraz możemy inwestować w lokaty
bankowe. Udowodnić, że ![]() jest rynkiem bez możliwości
arbitrażu wtedy i tylko wtedy, gdy ceny kontraktów futures i forward
są równe.
jest rynkiem bez możliwości
arbitrażu wtedy i tylko wtedy, gdy ceny kontraktów futures i forward
są równe.




