Zagadnienia

9.1 Aksjomaty procesu cen
9.2 Klasyczny model Blacka-Scholesa
9.3 Rynkowa cena ryzyka.
9.4 Zagadnienia i zadania na ćwiczenia

9. Model Blacka-Scholesa

Od tego rozdziału zajmiemy się badaniem rynku z czasem ciągłym. Zaczniemy od opisu procesu cen, a następnie zdefiniujemy model Blacka-Scholesa.

9.1. Aksjomaty procesu cen

W 1900 roku L. Bachelier zaproponował, żeby dynamikę ceny akcji na giełdzie paryskiej modelować za pomocą procesów otrzymanych z przejść granicznych błądzeń losowych, a więc zaproponował modelowanie ceny ciągłymi procesami $S_{t}$ o przyrostach niezależnych, takimi że przy zmianie czasu o $\Delta t$ zmiana ceny $S_{{t+\Delta t}}-S_{t}$ zachowuje się jak $\sqrt{\Delta t}$ dla małych przyrostów $\Delta t$ . We współczesnym języku matematyki jego postulaty oznaczają, że proces cen powinien mieć postać:

$S_{t}=S_{0}+\mu t+\sigma W_{t},$

gdzie $W_{t}$ jest procesem Wienera, $\mu\in\mathbb{R}$ , $\sigma>0$ . Zatem $S_{t}$ ma rozkład normalny ze średnią $S_{0}+\mu t$ i wariancją $\sigma^{2}t$ , co będziemy oznaczać $S_{t}\sim{\cal N}(S_{0}+\mu t,\sigma^{2}t).$ Stąd wynika, że cena akcji może przyjmować ujemne wartości z dodatnim prawdopodobieństwem. W związku z tym wiele osób odrzuca ten sposób modelowania ceny (zauważmy jednak, że z reguły trzech sigm wynika, że dla małych $t$ szanse na ujemną cenę są znikome, bo $P(S_{0}-3\sigma\sqrt{t}\leq S_{t}\leq S_{0}+3\sigma\sqrt{t})\approx 0{,}997$ , a ponadto często w statystyce używa się rozkładu normalnego do modelowania wielkości z istoty rzeczy nieujemnych np. długości, co nie wzbudza wątpliwości). Inną konsekwencją przyjęcia modelu Bacheliera jest fakt, że rozkład przyrostu ceny na ustalonym przedziale czasowym jest taki sam, niezależnie od ceny początkowej. Dlatego szansa, że cena akcji sprzedawanej po 50 jednostek spadnie w tym okresie do 45 (strata w wysokości 10% wartości) jest taka sama, jak szansa, że akcja w ustalonym okresie czasu warta 10 spadnie do 5 (strata w wysokości 50% wartości). Praca Bacheliera była zbyt nowatorska jak na ówczesne czasy i bardzo szybko została zapomniana. Odkryto ją ponownie dopiero w latach siedemdziesiątych dwudziestego wieku.

W 1965 r. Samuelson zaproponował postulaty, które powinien spełniać proces cen $S_{t}$ :

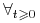
Ceny są dodatnie, czyli 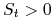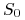$\forall _{{t\geq 0}}$ $S_{t}>0$ , $S_{0}$ jest stałą.
Procentowa zmiana cen akcji nie zależy od ceny obecnej ani od cen w przeszłości, czyli

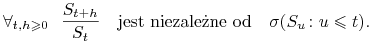
$\forall _{{t,h\geq 0}}\ \ \frac{S_{{t+h}}}{S_{t}}\quad\hbox{jest niezależne od}\quad\sigma(S_{u}\colon u\leq t).$
Zmiana ta (a dokładniej rozkład zmiany) zależy tylko od długości odcinka czasu, na którym jest rozpatrywana, natomiast nie jest istotne, od którego momentu ją liczymy, tj.

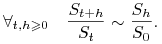
$\forall _{{t,h\geq 0}}\quad\frac{S_{{t+h}}}{S_{t}}\sim\frac{S_{h}}{S_{0}}.$
Proces $S_{t}$ ma ciągłe trajektorie.

Przy założeniach 1–4 można udowodnić, że proces cen wyraża się przez tzw. geometryczny proces Wienera (gdyż z postulatów wynika, że $\ln S_{t}$ jest procesem stacjonarnym o przyrostach niezależnych i o ciągłych trajektoriach)

$S_{t}=S_{0}\exp(at+\sigma W_{t}),\quad a\in\mathbb{R},\sigma>0.$

(9.1)

Pozostaje problem doboru stałych $a,\sigma$ by wzór (9.1) miał sens ekonomiczny. Okazuje się, że należy wziąć $\sigma>0$ i $a=(\mu-\frac{\sigma^{2}}{2})$ dla pewnego $\mu\in\mathbb{R}$ . Wtedy

$S_{t}=S_{0}\exp\Big(\Big(\mu-\frac{\sigma^{2}}{2}\Big)t+\sigma W_{t}\Big).$

(9.2)

Zatem $S_{t}$ ma rozkład lognormalny, tj.

$\ln S_{t}\sim N\Big(\ln S_{0}+\Big(\mu-\frac{\sigma^{2}}{2}\Big)t,\sigma^{2}t\Big).$

(9.3)

Znajdziemy teraz ekonomiczny sens stałych $\mu$ , $\sigma$ . Gdy $V_{t}$ jest wartością jakiegoś portfela w chwili $t$ , to dla $s<t$

$\frac{1}{t-s}E\Big(\frac{V_{t}-V_{s}}{V_{s}}\Big)$

jest oczekiwaną stopą zwrotu na jednostkę czasu z tego portfela w czasie od $s$ do $t$ . Wariancja stopy zwrotu na jednostkę czasu wyraża się wzorem

$\frac{1}{t-s}D^{2}\Big(\frac{V_{t}-V_{s}}{V_{s}}\Big).$

Gdy portfel składa się z jednej akcji, to oczywiście $V_{t}=S_{t}$ . Jeśli proces $S$ jest geometrycznym procesem Wienera, tj. $S_{t}$ spełnia (9.2), to łatwo udowodnić, że

			$\displaystyle\lim _{{u\to t^{-}}}\ \frac{1}{t-u}E\Big(\frac{S_{t}-S_{u}}{S_{u}}\Big)=\mu,$
			$\displaystyle\lim _{{u\to t^{-}}}\ \frac{1}{t-u}D^{2}\Big(\frac{S_{t}-S_{u}}{S_{u}}\Big)=\sigma^{2}.$

Stąd $\mu$ , odzwierciedlające stałe tendencje zmian cen akcji, nazywa się współczynnikiem wzrostu (stopą aprecjacji) cen akcji, a $\sigma$ mierzące zmienność nazywa się współczynnikiem zmienności cen akcji (dowód tych faktów pozostawiamy jako zadanie — zad. 9.3). W praktyce wielkość $\sigma$ podaje się w procentach.

9.2. Klasyczny model Blacka-Scholesa

Teraz opiszemy klasyczny model Blacka-Scholesa (Blacka-Mertona-Scholesa) z horyzontem $T<\infty$ . Niech $(\Omega,{\cal F},P)$ będzie przestrzenią probabilistyczną z filtracją $\mathbb{F}=({\cal F}_{t})_{{t\in[0,T]}}$ , na której mamy zadany proces Wienera $W$ . Zakładamy, że mamy do czynienia z rynkiem idealnym, na którym mamy jeden papier ryzykowny, akcje nie płacące dywidend, o cenie zadanej wzorem

$dS_{t}=\mu S_{t}dt+\sigma S_{t}dW_{t},\quad\sigma>0,\mu\in\mathbb{R}.$

(9.4)

W §9.1 uzasadniliśmy taki wybór procesu cen. Na tym rynku mamy także rachunek bankowy o stałej stopie procentowej $r\geq 0$ w całym okresie handlu $[0,T]$ i ciągłej kapitalizacji, tj. proces wartości jednostki pieniężnej jest zadany równaniem

$dB_{t}=rB_{t}dt,\quad B_{0}=1,$

zatem $B_{t}=e^{{rt}}$ . Rynek jest idealny, wszyscy mają taką samą wiedzę, a że informacje w naszym modelu są otrzymywane wyłącznie z obserwacji procesu cen $S$ to o $\sigma$ -ciele ${\cal F}_{t}$ interpretowanym jako wiedza uzyskana do chwili $t$ zakładamy, że ${\cal F}_{t}={\cal F}_{t}^{S}$ . Ponieważ jedynym rozwiązaniem (9.4) jest

$S_{t}=S_{0}\exp\,\Big(\sigma W_{t}+\Big(\mu-\frac{1}{2}\sigma^{2}\Big)t\Big),$

(9.5)

więc ${\cal F}_{t}^{W}={\cal F}_{t}^{S}$ . Podsumowując zakładamy, że filtracja ${\cal F}_{t}$ jest uzupełnioną filtracją procesu Wienera, tj. ${\cal F}_{t}={\cal F}_{t}^{W}$ i ${\cal F}={\cal F}_{T}$ .

Ten model jest znacznym uproszczeniem rzeczywistości. Jego zaletą są proste założenia zrozumiałe dla wszystkich. Stąd służy on jako pierwsze przybliżenie. Wzory (np. na ceny opcji) i reguły otrzymane dla tego modelu są używane w praktyce w bardziej wyrafinowany sposób.

Konstrukcję modelu rynku zaczynamy od definicji strategii.

Definicja 9.1

Strategią nazywamy proces mierzalny adaptowany $\varphi=(\varphi^{0},\varphi^{1})$ spełniający warunki

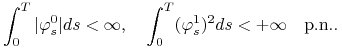$\int _{0}^{T}|\varphi _{s}^{0}|ds<\infty,\quad\int _{0}^{T}(\varphi^{1}_{s})^{2}ds<+\infty\quad\hbox{p.n.}.$

(9.6)

Jak zawsze $\varphi^{0}$ interpretujemy jako liczbę jednostek bankowych, a $\varphi^{1}$ jako liczbę akcji. Strategia $\varphi$ jest $\mathbb{F}$ adaptowana tzn. dla każdego $t$ wektor losowy $\varphi _{t}$ jest ${\cal F}_{t}$ mierzalny, zatem strategię tworzymy na podstawie wiedzy dostępnej do chwili $t$ . Proces wartości portfela (strategii) też definiujemy jak zwykle, tj.

$V_{t}(\varphi)=\varphi _{t}^{0}B_{t}+\varphi _{t}^{1}S_{t}.$

Proces zysków kapitałowych zadany jest przez odpowiednik (3.2):

$G_{{t}}(\varphi)=\int _{0}^{{t}}\varphi^{0}_{{u}}dB_{{u}}+\int _{0}^{{t}}\varphi _{{u}}^{{1}}dS_{{u}},\quad t\in[0,T].$

Warto zauważyć, że z postaci równania zadającego proces cen wynika, że

$\int _{0}^{{t}}\varphi _{{u}}^{{1}}dS_{{u}}=\int _{0}^{{t}}\varphi _{{u}}^{{1}}\mu S_{u}du+\int _{0}^{{t}}\varphi _{{u}}^{{1}}\sigma S_{u}dW_{{u}}.$

Warunek (9.6) oraz fakt, że cena $S$ jest procesem ciągłym zapewniają istnienie całek występujących w definicji procesu zysku.

Definicja 9.2

Mówimy, że strategia $\varphi$ jest samofinansująca się, gdy zachodzi

$\forall t\in[0,T]\quad V_{{t}}(\varphi)=V_{0}(\varphi)+G_{{t}}(\varphi).$

(9.7)

Warunek (9.7) jest równoważny warunkowi:

$V_{{t}}(\varphi)=V_{0}(\varphi)+\int _{0}^{{t}}\varphi^{0}_{{u}}rB_{{u}}du+\int _{0}^{{t}}\varphi^{1}_{{u}}\mu S_{{u}}du+\int _{0}^{{t}}\varphi^{1}_{{u}}\sigma S_{{u}}dW_{u},$

czyli

$dV_{{t}}(\varphi)=\varphi^{0}_{{t}}dB_{{t}}+\varphi^{1}_{{t}}dS_{{t}}=\varphi^{0}_{{t}}rB_{{t}}dt+\varphi^{1}_{{t}}\mu S_{{t}}dt+\varphi^{1}_{{t}}\sigma S_{{t}}dW_{t}.$

Intuicyjnie, portfel $\varphi$ jest samofinansujący się, gdy nie ma dopływu kapitału z zewnątrz — zmiany wartości portfela wynikają tylko z naszej polityki, czyli z postaci portfela $\varphi$ i ze zmian cen $S$ . Warunek (9.7) jest ciągłym odpowiednikiem warunku (3.5). Klasa wszystkich strategii samofinansujących się jest przestrzenią liniową. Będziemy ją oznaczać przez $\Phi$ .

Przykład 9.1

Strategia ,,kup i trzymaj aktywo” (buy-and-hold), czyli $\varphi _{t}^{1}\equiv a>0$ , $\varphi _{t}^{0}\equiv 0$ jest strategią samofinansującą się, bo

	$\displaystyle V_{t}(\varphi)$	$\displaystyle=$	$\displaystyle\varphi _{t}^{1}S_{t}=aS_{t},$
	$\displaystyle G_{t}(\varphi)$	$\displaystyle=$	$\displaystyle\int _{0}^{t}a~dS_{u}=a(S_{t}-S_{0}),$

a stąd

$V_{t}(\varphi)=aS_{0}+G_{t}(\varphi)=V_{0}(\varphi)+G_{t}(\varphi).$

Ćwiczenie 9.1

Udowodnić, że strategia $\varphi _{t}^{0}=\frac{S_{t}}{B_{t}}$ , $\varphi _{t}^{1}\equiv 0$ ma portfel bogactwa równy $V_{t}(\varphi)=S_{t}$ (a więc taki sam jak strategia ,,kup i trzymaj”), ale nie jest strategią samofinansującą się.

Rozwiązanie:

Z postaci strategii $\varphi$ mamy $V_{t}(\varphi)=S_{t}$ , a z postaci $B_{t}$ mamy

$G_{t}(\varphi)=\int _{0}^{t}\varphi _{u}^{0}\ dB_{u}=\int _{0}^{t}\frac{S_{u}}{B_{u}}\ dB_{u}=r\int _{0}^{t}S_{u}du,$

i korzystając z definicji strategii samofinansującej się (tj. z (9.7)) otrzymujemy, że $\varphi\in\Phi$ wtedy i tylko wtedy gdy zachodzi warunek

$S_{t}=S_{0}+r\int _{0}^{t}\ S_{{u}}du.$

(9.8)

Warunek (9.8) nie jest spełniony w modelu Blacka-Scholesa.

Definicja arbitrażu i jego sens jest analogiczny jak dla rynku skończonego.

Definicja 9.3

Możliwością arbitrażu $($ arbitrażem $)$ nazywamy strategię $\varphi\in\Phi$ taką, że

$V_{0}(\varphi)=0,\quad P(V_{T}(\varphi)\geq 0)=1,\quad P(V_{T}(\varphi)>0)>0$

(9.9)

dla pewnego $P\in{\cal P}$ .

Ponieważ zbiory miary zero pozostają te same dla każdego $P\in{\cal P}$ , więc jeśli (9.9) zachodzi dla pewnego $P\in{\cal P}$ , to zachodzi dla każdego $P\in{\cal P}$ . Arbitraż jest sposobem postępowania, który nigdy nie przyniesie straty i daje możliwość osiągnięcia zysku w sprzyjających okolicznościach. Gdy na rynku istnieje możliwość arbitrażu, to odpowiednio postępując można osiągać na nim zysk bez ryzyka. Istnienie arbitrażu świadczy o braku równowagi na rynku. Na istniejących rynkach finansowych działają arbitrażyści i nie ma możliwości arbitrażu. Zatem modele opisujące rzeczywistość powinny być wolne od arbitrażu.

Zajmiemy się teraz pojęciem wypłaty.

Definicja 9.4

Wypłatą europejską $($ aktywem pochodnym lub kontraktem europejskim $)$ z momentem wykonania $T$ nazywamy zmienną losową $X$ .

Wypłatę $X$ otrzymuje kupujący w chwili $T,$ jest to zmienna losowa, więc jest ona ${\cal F}_{T}$ -mierzalna, czyli jest skonstruowana w oparciu o dostępną wiedzę do chwili $T$ , a zatem jej wartość zależy od procesu cen. Jak zawsze, pojawia się pytanie: jeśli w momencie $T$ kupujący otrzymuje $X$ , to ile powinien zapłacić za to teraz? By na nie odpowiedzieć, wprowadzamy, jak dla rynków skończonych, pojęcie strategii replikującej. Mówimy, że $\varphi\in\Phi$ jest strategią replikującą wypłatę $X$ w chwili $T$ gdy $V_{T}(\varphi){=}X$ (strategia $\varphi$ jest zabezpieczeniem wypłaty $X$ ). Jeśli wypłata $X$ ma choć jedną strategię replikującą, to mówimy, że $X$ jest osiągalna. Analogicznie jak dla rynku skończonego wprowadzamy pojęcie bogactwa wypłaty osiągalnej (tzn. pojęcie jednoznacznej replikowalności), a mianowicie mówimy, że istnieje proces bogactwa osiągalnej wypłaty $X$ , gdy dla każdych strategii $\varphi,\psi\in\Phi$ , takich, że $V_{T}(\varphi)=V_{T}(\psi)=X$ procesy $V(\varphi)$ i $V(\psi)$ są nieodróżnialne (tzn. $P(\forall t\leq T:V_{t}(\varphi)=V_{t}(\psi))=1$ ).

Definicja 9.5

Niech $\Psi\subset\Phi$ . Na rynku ${\cal M}=(B,S,\Psi)$ bez możliwości arbitrażu ceną arbitrażową $\Pi _{t}(X)$ w chwili $t$ osiągalnej wypłaty europejskiej $X$ dla której istnieje proces bogactwa nazywamy wartość w chwili $t$ strategii samofinansującej się replikującej wypłatę tzn. $\Pi _{t}(X)=V_{t}(\varphi).$

Uwaga 9.1

Wybór klasy strategii $\Psi\subset\Phi$ jest istotny. Nie można wziąć, jak dla rynku skończonego, $\Psi=\Phi$ , gdyż prowadzi to do arbitrażu. Zatem musimy dokonać sensownego wyboru jakiejś podklasy $\Psi$ strategii samofinansujących się $\Phi$ . Wyborem podklasy $\Psi$ zajmiemy się pózniej.

Taka definicja ceny jest uzasadniona faktem, że dla inwestora jest obojętne, czy ma w swym portfelu instrument finansowy, czy wartość początkową strategii generującej go, gdyż w obu przypadkach otrzymuje na końcu okresu inwestycji tę samą wypłatę (w drugim przypadku musi postępować tak, jak wskazuje strategia replikująca). Można udowodnić wprost, że definicja ceny jest poprawna tzn. że dla każdej wypłaty osiągalnej istnieje proces bogactwa. My to udowodnimy korzystając z idei miary martyngałowej. Wszystkie ceny będziemy dyskontować przez wartość jednostki bankowej, tj.

$B^{*}_{t}=\frac{B_{t}}{B_{t}}\equiv 1,\qquad S_{t}^{*}=\frac{S_{t}}{B_{t}}=S_{t}e^{{-rt}}.$

Definicja 9.6

Miarę probabilistyczną $P^{*}$ na $(\Omega,{\cal F}_{T})$ nazywamy miarą martyngałową, gdy $P^{*}\sim P$ i $S^{*}$ jest $P^{*}$ -martyngałem lokalnym.

Zaczniemy od twierdzenia podającego postać miary martyngałowej dla zdyskontowanego procesu cen $S^{*}$ .

Twierdzenie 9.1

Miara probabilistyczna $P^{*}$ o gęstości

$\frac{dP^{*}}{dP}=\exp\Big(\frac{r-\mu}{\sigma}W_{T}-\frac{1}{2}\Big(\frac{r-\mu}{\sigma}\Big)^{2}T\Big)$

(9.10)

jest jedyną miarą martyngałową. Ponadto proces $S^{*}$ jest $P^{*}$ -martyngałem o dynamice

$dS_{t}^{*}=\sigma S_{t}^{*}d{\widehat{W}}_{t},\quad S_{0}^{*}=s,$

(9.11)

gdzie ${\widehat{W}}_{t}=W_{t}-\frac{r-\mu}{\sigma}t$ jest procesem Wienera względem $P^{*}$ i filtracji $\mathbb{F}$ .

Ponieważ $S_{t}^{*}=S_{t}e^{{-rt}}$ , więc ze wzoru na całkowanie przez części

$dS_{t}^{*}=S_{t}(-re^{{-rt}})dt+e^{{-rt}}dS_{t}.$

(9.12)

Zatem, korzystając z dynamiki $S$ tzn. (9.4), otrzymujemy

$dS_{t}^{*}=e^{{-rt}}(-rS_{t}dt+\mu S_{t}dt+\sigma S_{t}dW_{t})=S_{t}^{*}((\mu-r)dt+\sigma dW_{t}).$

Chcemy, by $dS_{t}^{*}=\sigma S_{t}^{*}d{\widehat{W}}_{t}$ dla procesu Wienera ${\widehat{W}}$ przy pewnej mierze $P^{*}$ . Zatem powinno zachodzić

$\sigma d{\widehat{W}}_{t}=\sigma dW_{t}-(r-\mu)dt.$

(9.13)

Na mocy tw. Girsanowa miara $P^{*}$ zadana wzorem (9.10) jest dobrze zdefiniowaną miarą probabilistyczną i ${\widehat{W}}_{t}=W_{t}-\frac{r-\mu}{\sigma}t$ jest procesem Wienera względem $P^{*}$ . Wtedy zachodzi (9.13), czyli zachodzi (9.11). Proces $S^{*}$ , przy mierze $P^{*}$ jest równy całce stochastycznej względem procesu Wienera plus stała, więc jest $P^{*}$ -martyngałem lokalnym, czyli $P^{*}$ jest miarą martyngałową dla $S^{*}$ . Jedyność $P^{*}$ pozostawiamy jako zadanie dla Czytelnika (zad. 9.10). Ponieważ

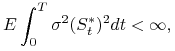$E\int _{0}^{T}\sigma^{2}(S^{*}_{t})^{2}dt<\infty,$

(9.14)

to $S^{*}$ jest $P^{*}$ -martyngałem.

∎

Uwaga 9.2

a) Warunek (9.11) można zapisać równoważnie

$dS_{t}=rS_{t}dt+\sigma S_{t}d{\widehat{W}}_{t},$

(9.15)

gdyż z (9.13) mamy

$dS_{t}=\mu S_{t}dt+\sigma S_{t}dW_{t}=rS_{t}dt+\sigma S_{t}d{\widehat{W}}_{t}.$

Zatem przy zamianie miary na równoważną miarę martyngałową współczynnik zmienności ceny akcji nie ulega zmianie.

b) Z (9.15) wynika, że przy mierze martyngałowej $P^{*}$ proces cen ma postać

$S_{t}=S_{0}\exp\Big(\sigma{\widehat{W}}_{t}+\Big(r-\frac{1}{2}\sigma^{2}\Big)t\Big).$

(9.16)

Analogicznie jak w przypadku rynku skończonego istnieje ważna charakteryzacja portfeli samofinansujących się w terminach procesu zdyskontowanych cen:

Twierdzenie 9.2

Strategia $\varphi=(\varphi^{0},\varphi^{1})$ jest strategią samofinansującą się wtedy i tylko wtedy, gdy zachodzi

$\forall t\in[0,T]\quad V_{t}^{*}(\varphi)=V_{0}(\varphi)+\int _{0}^{t}\varphi _{u}^{1}dS_{u}^{*}.$

(9.17)

$\ \Rightarrow\$ Konieczność. Ponieważ

$V_{t}^{*}(\varphi)=V_{t}(\varphi)e^{{-rt}},$

(9.18)

więc kolejno ze wzoru na całkowanie przez części, definicji strategii samofinansującej się i (9.12) mamy

$\displaystyle dV_{t}^{*}(\varphi)$	$\displaystyle=$	$\displaystyle-re^{{-rt}}V_{t}(\varphi)dt+e^{{-rt}}dV_{t}(\varphi)=$
	$\displaystyle=$	$\displaystyle-re^{{-rt}}(\varphi^{0}_{{t}}B_{{t}}+\varphi^{1}_{t}S_{t})dt+e^{{-rt}}(\varphi^{0}_{{t}}dB_{{t}}+\varphi^{1}_{t}dS_{t})=$
	$\displaystyle=$	$\displaystyle\varphi^{1}_{t}(-re^{{-rt}}S_{t}dt+e^{{-rt}}dS_{t})=\varphi^{1}_{t}dS_{t}^{*}.$

Zatem równość (9.17) jest spełniona.
Dostateczność. Z (9.18) mamy

$dV^{*}_{t}(\varphi)=-re^{{-rt}}(\varphi^{0}_{{t}}B_{{t}}+\varphi^{1}_{t}S_{t})dt+e^{{-rt}}dV_{t}(\varphi).$

(9.19)

Ze wzoru (9.12) otrzymujemy

$\varphi^{1}_{t}dS_{t}^{*}=-re^{{-rt}}S_{t}\varphi^{1}_{t}dt+e^{{-rt}}\varphi^{1}_{t}dS_{t}.$

(9.20)

Z założenia (9.17) wynika, że lewe strony wzorów (9.19) i (9.20) są równe, więc i prawe są równe, zatem

$dV_{t}(\varphi)=\varphi^{0}_{{t}}dB_{{t}}+\varphi^{1}_{t}dS_{t},$

czyli $\varphi\in\Phi$ .

∎

Lemat ten wykorzystuje się do znajdowania strategii samofinansujących się replikujących daną wypłatę. Z niego wynika także:

Twierdzenie 9.3

Miara $P^{*}$ jest miarą martyngałową dla $S^{*}$ wtedy i tylko wtedy, gdy dla każdej strategii samofinansującej się $\varphi$ zdyskontowany proces bogactwa $V^{*}(\varphi)$ jest $P^{*}$ -martyngałem lokalnym.

Konieczność. Korzystając z (9.11) i (9.17) mamy

$V_{t}^{*}(\varphi)=V_{0}(\varphi)+\int _{0}^{t}\varphi _{u}^{1}dS_{u}^{*}=V_{0}(\varphi)+\int _{0}^{t}\varphi _{u}^{1}\sigma S_{u}^{*}d{\widehat{W}}_{t},$

a ponieważ ${\widehat{W}}$ jest $P^{*}$ procesem Wienera, to $V^{*}(\varphi)$ jest $P^{*}$ -martyngałem lokalnym.
Dostateczność. Biorąc strategię stałą $\varphi^{0}\equiv 0,\varphi^{1}\equiv 1$ otrzymujemy, że $\varphi\in\Phi$ i $S^{*}_{t}=V^{*}_{t}(\varphi)$ . $V^{*}(\varphi)$ jest $P^{*}$ -martyngałem lokalnym z założenia, czyli $S^{*}$ jest $P^{*}$ -martyngałem lokalnym.

∎

Rozpatrywanie rynku ze wszystkimi możliwymi strategiami samofinansującymi się prowadzi do arbitrażu. Zatem, by wykluczyć arbitraż, ograniczamy klasę strategii do strategii dopuszczalnych

Definicja 9.7

Niech $P^{*}$ będzie miarą martyngałową dla $S^{*}$ . Strategię $\varphi\in\Phi$ nazywamy dopuszczalną ( $P^{*}$ –dopuszczalną), gdy proces

$\int _{0}^{t}\varphi^{1}_{u}dS^{*}_{u}$

jest $P^{*}$ -martyngałem.

Ponieważ dla $S^{*}$ istnieje dokładnie jedna miara martyngałowa, to mówimy, że $\varphi$ jest dopuszczalna (zamiast $P^{*}$ –dopuszczalna), gdyż nie ma wątpliwości o jaką miarę martyngałową chodzi. Zbiór takich strategii będziemy oznaczać przez $\Phi(P^{*})$ .

Uwaga 9.3

Gdy $\varphi\in\Phi$ , to z warunku (9.17) wynika, że

$V_{t}^{*}(\varphi)=V_{0}^{*}(\varphi)+\int _{0}^{t}\varphi^{1}_{u}dS_{u}^{*},$

a stąd jeśli $\varphi\in\Phi(P^{*})$ , to proces $V_{t}^{*}(\varphi)$ jest $P^{*}$ -martyngałem.

Udowodnimy teraz, że wzięcie $\Psi=\Phi(P^{*})$ jest dobrym wyborem klasy portfeli.

Twierdzenie 9.4

Rynek $(B,S,\Phi(P^{*}))$ jest wolny od arbitrażu.

Weźmy $\varphi\in\Phi(P^{*})$ takie, że $V_{0}(\varphi)=0$ i $P(V_{T}(\varphi)\geq 0)=1$ . Udowodnimy, że $P(V_{T}(\varphi)=0)=1$ , więc $\varphi$ nie jest arbitrażem, a zatem na rynku $(S,\Phi(P^{*}))$ nie istnieje arbitraż.

Z założenia $V^{*}(\varphi)$ jest $P^{*}$ -martyngałem, wobec tego

$E_{{P^{*}}}V_{T}^{*}(\varphi)=E_{{P^{*}}}V_{0}(\varphi)=0.$

(9.21)

Ponieważ $P^{*}(V_{T}(\varphi)\geq 0)=1$ (bo $P\sim P^{*}$ ), $B_{T}>0$ , więc (9.21) implikuje $P^{*}(V_{T}(\varphi)=0)=1$ , a stąd z równoważności miar $P$ i $P^{*}$ otrzymujemy $P(V_{T}(\varphi)=0)=1$ .

∎

Definicja 9.8

Trójkę ${\cal M}=(B,S,\Phi(P^{*}))$ nazywamy klasycznym modelem Blacka-Scholesa rynku finansowego (w skrócie modelem Blacka-Scholesa; niektórzy autorzy używaja nazwy model Blacka-Mertona-Scholesa).

9.3. Rynkowa cena ryzyka.

Załóżmy, że na rynku Blacka-Scholesa bez możliwości arbitrażu mamy dodatkowy instrument pierwotny, zatem mamy dwa instrumenty pierwotne, którymi możemy handlować i których ceny zadane są względem jednowymiarowego procesu Wienera $W$ (tego samego) równaniami

$dS_{t}^{{(i)}}=S_{t}^{{(i)}}(\mu _{i}dt+\sigma _{i}dW_{t}),\quad i=1,2,$

czyli na tym rynku mamy jedno źródło losowości — proces Wienera $W$ i rynek rozszerzony jest rynkiem bez możliwości arbitrażu. Gdy $P^{*}$ jest miarą martyngałową dla rynku Blacka-Scholesa $(B,S^{{(1)}},\Phi(P^{*}))$ , to

$\widehat{W_{t}}=W_{t}-\Big(\frac{r-\mu _{1}}{\sigma _{1}}\Big)t$

jest $P^{*}$ -procesem Wienera. Ponadto

$dS_{t}^{{(2)*}}=S_{t}^{{(2)*}}((\mu _{2}-r)dt+\sigma _{2}dW_{t})=S_{t}^{{(2)*}}\Big(\Big((\mu _{2}-r)+\frac{r-\mu _{1}}{\sigma _{1}}\sigma _{2}\Big)dt+\sigma _{2}d{\widehat{W}}_{t}\Big),$

a ponieważ proces $S^{{(2)*}}$ jest $P^{*}$ -martyngałem, więc

$(\mu _{2}-r)+\frac{r-\mu _{1}}{\sigma _{1}}\sigma _{2}=0.$

Stąd

$\frac{\mu _{1}-r}{\sigma _{1}}=\frac{\mu _{2}-r}{\sigma _{2}}.$

Gdy proces ceny $S$ jest zadany wzorem (9.2), to wielkość

$\gamma=\frac{\mu-r}{\sigma}$

ekonomiści nazywają rynkową ceną ryzyka (przez analogię do modelu CAPM) — jest to nadwyżka średniego zwrotu z akcji ponad zwrot z instrumentu bez ryzyka mierzona w jednostkach ryzyka. Wykazaliśmy, że instrumenty bazowe, którymi można handlować na rozszerzonym rynku Blacka-Scholesa bez możliwości arbitrażu z instrumentami bazowymi o cenach zadanych wzorem (9.2) (z różnymi parametrami) mają tę samą rynkową cenę ryzyka. Warto zauważyć, że ta terminologia została tu użyta w innym sensie niż dotąd: nie jest to cena arbitrażowa jakiegoś jednego instrumentu, którym możemy handlować na rynku.

Ponieważ $\widehat{W_{t}}=W_{t}+\gamma t$ , więc $\gamma$ wyznacza gęstość miary martyngałowej $P^{*}$ względem $P$

$\frac{dP^{*}}{dP}=\exp\Big(-\gamma W_{T}-\frac{1}{2}\gamma^{2}T\Big)$

i stąd miara $P^{*}$ jest nazywana miarą neutralną względem ryzyka.

9.4. Zagadnienia i zadania na ćwiczenia

Ćwiczenie 9.2

Udowodnić, że proces spełniający postulaty 1–4 z §9.1 jest zadany wzorem (9.1).

Ćwiczenie 9.3

Wykazać, że gdy $S_{t}$ spełnia (9.2), to

			$\displaystyle\lim _{{u\to t^{-}}}\frac{1}{t-u}E\Big(\frac{S_{t}-S_{u}}{S_{u}}\Big)=\mu,$
			$\displaystyle\lim _{{u\to t^{-}}}\frac{1}{t-u}D^{2}\Big(\frac{S_{t}-S_{u}}{S_{u}}\Big)=\sigma^{2}.$

Wskazówka:

Skorzystać z faktu, że gdy $X\sim{\cal N}(\mu,\sigma^{2})$ , $Y=e^{X}$ , to $EY=e^{{\mu+\frac{\sigma^{2}}{2}}}$ , $D^{2}(Y)=e^{{2\mu+\sigma^{2}}}(e^{{\sigma^{2}}}-1).$

Rozwiązanie:

$\frac{S_{t}-S_{u}}{S_{u}}=\exp\Big((t-s)\Big(\mu-\frac{\sigma^{2}}{2}\Big)+\sigma(W_{t}-W_{s})\Big)-1,$

więc korzystając z faktu podanego we wskazówce znajdujemy wartość oczekiwaną i wariancję tego ułamka. Reszta jest prostym przejściem do granicy.

Ćwiczenie 9.4

Pokazać, że średnia wartość ceny rośnie ze stopą równą $\mu$ , czyli $ES_{t}=S_{0}e^{{t\mu}}$ . Stąd wynika, że gdy średnia stopa zwrotu z akcji ma być taka sama jak dla papierów bez ryzyka, to $\mu=r$ .

Wskazówka:

Skorzystać ze wskazówki do poprzedniego zadania.

Ćwiczenie 9.5

Rozważmy na rynku Blacka-Scholesa akcję z ceną początkową 40, oczekiwanym zwrotem 16% p.a., współczynnikiem zmienności 20% p.a. (na rynku te wielkości podaje się w procentach). Znaleźć:

a) 95% przedział ufności dla ceny akcji za trzy miesiące.

b) średnią cenę akcji za trzy miesiące.

Rozwiązanie:

Z warunków zadania mamy $\mu=0{,}16$ , $\sigma=0{,}2$ , $S_{0}=40$ , $t=1/4$ . Z (9.3) wynika, że $\ln S_{t}$ ma rozkład normalny, a jak wiemy, 95% przedział ufności dla zmiennej losowej o rozkładzie normalnym ${\cal N}(m,\sigma^{2})$ ma postać $(m-2\sigma,m+2\sigma)$ . Stąd, po rachunkach, otrzymujemy przedział ufności: $(34{,}05;50{,}39)$ . Z ćw. 9.3 otrzymujemy $ES_{t}=41{,}63$ .

Ćwiczenie 9.6

Udowodnić, że proces cen $S_{t}$ spełniający (9.2) jest opisany za pomocą równania

$dS_{t}=\mu S_{t}dt+\sigma S_{t}dW_{t}.$

Rozwiązanie:

Stosujemy wzór Itô do funkcji $f(x)=e^{x}$ i procesu $X$ zadanego stochastycznym równaniem różniczkowym

$dX_{t}=\Big(\mu-\frac{\sigma^{2}}{2}\Big)dt+\sigma dW_{t}$

(wtedy $S_{t}=f(X_{t})).$

Ćwiczenie 9.7

Udowodnić, że portfel stały jest strategią samofinansującą się.

Rozwiązanie:

Portfel stały jest kombinacją liniową strategii ,,kup i trzymaj” oraz włóż pieniądze do banku, które są strategiami samofinansującymi się (przykład 9.1), a więc portfel stały jest strategią samofinansującą się.

Ćwiczenie 9.8

Analogicznie jak w czasie dyskretnym, znając strategię inwestowania w papiery ryzykowne i kapitał początkowy, znamy całą strategię samofinansującą się. Formalnie: udowodnić, że dla każdego $x\in\mathbb{R}$ i procesu prognozowalnego $\varphi^{1}$ takiego, że całka $\int\varphi^{1}dS^{{*}}$ istnieje, przyjęcie

$\varphi^{0}_{t}=x+\int _{0}^{t}\varphi _{u}^{1}dS_{u}^{{*}}-\varphi _{t}^{1}S_{t}^{{*}}$

definiuje jednoznacznie portfel samofinansujący się $\varphi=(\varphi^{0},\varphi^{1})\in\Phi$ , taki, że $V_{0}(\varphi)=x$ .

Ćwiczenie 9.9

Udowodnić, że jeśli rynek $(S,\Psi)$ dla $t\in[0,T]$ jest wolny od arbitrażu, to rynek $(S,\Psi)$ dla $t\in[0,T_{1}]$ , gdzie $T_{1}<T$ , jest wolny od arbitrażu.

Rozwiązanie:

Jeśli istnieje arbitraż $\varphi$ dla $t\in[0,T_{1}]$ , to inwestując w chwili $T_{1}$ całe bogactwo $V_{{T_{1}}}^{*}(\varphi)$ w aktywa bez ryzyka otrzymujemy strategię arbitrażową dla rynku z czasem $[0,T]$ .

Ćwiczenie 9.10

Udowodnić, że dla klasycznego rynku Blacka-Scholesa istnieje dokładnie jedna miara martyngałowa.

Ćwiczenie 9.11

Udowodnić, że na rynku Blacka-Scholesa strategia ,,kup i trzymaj aktywo” (patrz przykł. 9.1) jest strategią dopuszczalną.

Rozwiązanie:

$G_{t}^{*}(\varphi)=\int _{0}^{t}\varphi _{t}^{1}dS_{u}^{*}=a(S_{t}^{{*}}-S_{0}^{{*}}),\quad a\in\mathbb{R}$ , więc $G_{t}^{*}(\varphi)$ jest $P^{*}$ martyngałem.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Modele matematyczne rynków instrumentów pochodnych I

Zagadnienia

9. Model Blacka-Scholesa

9.1. Aksjomaty procesu cen

9.2. Klasyczny model Blacka-Scholesa

Definicja 9.1

Definicja 9.2

Przykład 9.1

Ćwiczenie 9.1

Definicja 9.3

Definicja 9.4

Definicja 9.5

Uwaga 9.1

Definicja 9.6

Twierdzenie 9.1

Uwaga 9.2

Twierdzenie 9.2

Twierdzenie 9.3

Definicja 9.7

Uwaga 9.3

Twierdzenie 9.4

Definicja 9.8

9.3. Rynkowa cena ryzyka.

9.4. Zagadnienia i zadania na ćwiczenia

Ćwiczenie 9.2

Ćwiczenie 9.3

Ćwiczenie 9.4

Ćwiczenie 9.5

Ćwiczenie 9.6

Ćwiczenie 9.7

Ćwiczenie 9.8

Ćwiczenie 9.9

Ćwiczenie 9.10

Ćwiczenie 9.11