Zagadnienia
1. Wprowadzenie
1.1. Wstęp
Prezentowany cykl wykładów stanowi elementarne wprowadzenie do modelowania rynków finansowych, do wyceny instrumentów pochodnych oraz zagadnień zabezpieczania wypłat. Celem jest przedstawienie podstawowych idei matematyki finansowej i rządzących nią mechanizmów. Zamierzam pokazać jak problemy praktyczne związane z wyceną aktywów bazowych i instrumentów pochodnych (a więc takich, których cena zależy od cen aktywów podstawowych) oraz zabezpieczeniem wypłat zapisać w języku matematyki, a następnie jak, korzystając z aparatu matematycznego, problemy te rozwiązać. Opis rynku, jak i praktyczne jego działanie, przedstawiono tylko w stopniu niezbędnym do konstrukcji modelu.
Przy badaniu instrumentów pochodnych skupimy się na wycenie i replikacji wypłat dających losowy zysk w ustalonej chwili końcowej w przyszłości. Przykładami takich wypłat są opcje europejskie i kontrakty terminowe. Korzystając z metod stochastycznych (teoria martyngałów i analiza stochastyczna) rozwiążemy postawione wyżej pytania.
W pierwszym rozdziale zostały opisane rynki finansowe i omówiono ważniejsze klasy instrumentów pochodnych. W drugim przeanalizowano najprostszy model rynku — model rynku jednookresowego dwustanowego.
W części drugiej, składającej się z 6 rozdziałów szczegółowo omówiono rynki skończone, czyli rynki z czasem dyskretnym i ze skończonym zbiorem stanów (scenariuszy). Na przykładzie tego rynku widać dobrze sens ekonomiczny założeń i myśl przewodnią koncepcji wyceny i replikacji. Do zrozumienia tej części skryptu wystarczająca jest znajomość elementarnej teorii martyngałów, np. z książki Jakubowskiego i Sztencla Wstęp do teorii prawdopodobieństwa [J-Sz].
Część trzecia wykładów opisuje rynki z czasem ciągłym.
Przedstawiono w niej klasyczny model Blacka-Scholesa w kontekście
ogólnej teorii rynku z czasem ciągłym. Zostały m.in. wyprowadzone
wzory Blacka-Scholesa. Omówiono metody szukania współczynnika
zmienności ![]() . Przedstawiono modele zmienności, opcje
amerykańskie, opcje egzotyczne, rynek kontraktów terminowych futures
(wzory Blacka).
. Przedstawiono modele zmienności, opcje
amerykańskie, opcje egzotyczne, rynek kontraktów terminowych futures
(wzory Blacka).
Wykłady bazują na podręczniku J. Jakubowskiego ”Modelowanie rynków finansowych”. Wybrana literatura składająca się z artykułów fundamentalnych dla dziedziny i wybranych podręczników jest podana w bibliografii umieszczonej na końcu prezentowanego cyklu wykładów. Jest to wybór subiektywny i niepełny, gdyż matematyka finansowa jest obecnie bardzo modną dziedziną i co roku powstaje wiele nowych podręczników i prac. Więcej informacji o praktycznym aspekcie działania rynków zawierają monografie Hulla Options, Futures, and Other Derivatives [Hull] oraz Jakubowskiego, Palczewskiego, Rutkowskiego i Stettnera Matematyka finansowa. Instrumenty pochodne [J-PRS]. Naturalnym uogólnieniem rynku skończonego jest odrzucenie założenia o skończonej liczbie scenariuszy. Otrzymujemy rynek z czasem dyskretnym, jednak do dowodów podstawowych faktów trzeba używać znacznie bardziej zaawansowanych technik. Czytelnik może zapoznać się z tym uogólnieniem w trzecim rozdziale książki [J-PRS] lub w książce Föllmera i Schieda Stochastic Finance, An Introduction in Discrete Time [Fol-S]. Dla opisu rynków z czasem ciągłym można polecić m.in. książki Shiryaeva Essentials of Stochastic Finance [Shi], Shrevea Stochastic calculus for finance II. Continuous-time models [Shreve].
1.2. Ogólny opis rynku
Istnieje wiele różnych rodzajów rynków finansowych, w zależności od instrumentów finansowych, którymi się na nich handluje. Najważniejsze to:
-
 Rynek kapitałowy (papiery wartościowe, akcje)
Rynek kapitałowy (papiery wartościowe, akcje) -
 Rynek pieniężny (kasowy) – instrumenty dłużne (lokaty/depozyty, bony, obligacje)
Rynek pieniężny (kasowy) – instrumenty dłużne (lokaty/depozyty, bony, obligacje) -
 Rynek instrumentów pochodnych
Rynek instrumentów pochodnych -
 Rynek walutowy – transakcje wymiany walut
Rynek walutowy – transakcje wymiany walut
Rynki możemy też podzielić na
-
giełda, miejsce gdzie dokonuje się obrót akcjami,
-
rynek obligacji,
-
rynek walutowy,
-
giełda towarowa — obejmuje m.in. takie towary, jak miedź, srebro, zboże, ropa naftowa.
Na wyżej wspomnianych rynkach handluje się papierami wartościowymi dwojakiego rodzaju: aktywami pierwotnymi i aktywami pochodnymi.
Aktywa, którymi bezpośrednio handluje się na rynku nazywać będziemy instrumentami pierwotnymi (aktywami, papierami). Używa się również terminu instrumenty bazowe. My skupimy się głównie na akcjach.
Akcje to papiery wartościowe dające posiadaczowi prawo do dywidendy (wypłaty z zysku) oraz do części majątku firmy. Ich wartość odzwierciedla rynkowe oczekiwania inwestorów co do prawdopodobnych przyszłych dywidend i przyszłego wzrostu kapitału firmy.
Aktywa pochodne definiuje się jako dowolne aktywa, których cena zależy od cen aktywów podstawowych. Zatem papiery pochodne to takie szczególne papiery wartościowe, których wartość jest ściśle związana z wahaniami ceny czynnika (instrumentu) bazowego. Czynnikiem owym mogą być np. ceny akcji, ceny obligacji rządowych, ceny obligacji hipotecznych, poziom stóp procentowych, giełdowe kursy walut.
Dwa podstawowe typy aktywów pochodnych to:
-
Opcje: dają one posiadaczowi opcji prawo do wykonania opcji (wykonanie nie jest obligatoryjne). Na przykład opcja kupna akcji ustalonej firmy daje prawo do kupna akcji tej firmy w ściśle określonym terminie (np. za 2 miesiące) i po ściśle określonej cenie. Gdy ceny akcji wzrosną ponad tę określoną cenę, posiadacz opcji kupna korzysta ze swoich praw i wykonuje opcję zyskując na różnicy. Gdy ceny spadną poniżej ustalonego poziomu, opcje stają się bezwartościowe — posiadacz opcji nie wykonuje opcji.
-
Kontrakty: obie strony transakcji muszą wypełnić swoje zobowiązanie.
Na rynkach finansowych można rozróżnić trzy podstawowe kategorie inwestorów, dzieląc ich według kryterium celu jaki chcą osiągnąć wchodząc na rynek:
-
Arbitrażyści, a więc inwestorzy, którzy chcą osiągnąć natychmiastowy zysk (zatem bez ryzyka zajścia niekorzystnego scenariusza mogącego zmienić ceny w przyszłości). Wychwytują oni i natychmiast wykorzystują wszelkie różnice cen instrumentów na rynku, które dają możliwości zarobku.
-
Inwestorzy, którzy chcą się zabezpieczyć przed niekorzystnymi zmianami cen na rynku.
-
Inwestorzy, którzy wchodzą na rynek chcąc zarobić więcej niż inwestując w lokatę bankową.
My zajmiemy się trzema rodzajami aktywów pochodnych, a mianowicie opcjami oraz kontraktami terminowymi forward i futures. Teraz zajmiemy się opisem opcji, kontrakty terminowe opiszemy dokładniej, gdy będziemy je wyceniać.
1.3. Opcje
Jak juz mówilismy, opcja jest to umowa między dwoma podmiotami.
Opcje kupna (call) dają posiadaczowi prawo do kupienia określonego w umowie aktywa w ustalonej chwili lub przez ustalony okres czasu za ustaloną cenę. Opcje sprzedaży (put) dają posiadaczowi prawo do sprzedaży określonego w umowie aktywa w ustalonej chwili (względnie przed ustalonym momentem) za ustaloną cenę.
Opcje mogą być wystawiane na akcje, indeksy akcji, towary, waluty obce, instrumenty dłużne, kontrakty terminowe itp. (możliwe są także opcje o charakterze zbliżonym do gry hazardowej, na przykład wystawione na warunki pogodowe). Opcje zawsze rozlicza się pieniężnie. Pierwszym elementem jaki opisuje się przy definiowaniu opcji jest cena wykonania. W kontrakcie kupna odnosi się ona do ceny, jaką płaci nabywca za aktywo, jeśli wykorzystuje swoje prawo do kupna. W kontrakcie sprzedaży jest to cena, za jaką właściciel opcji sprzedaje aktywo, jeśli wykorzystuje swoje prawo. Cena ta jest ustalana w chwili wystawienia opcji i nie podlega zmianie. Skorzystanie z prawa do zakupu lub sprzedaży określa się mianem wykonania lub rozliczenia opcji.
Opcja jest ważna do momentu wygaśnięcia. Termin wykonania opcji jest dokładnie zdefiniowany w kontrakcie. Przykładowo, jest równy momentowi wygaśnięcia w przypadku tzw. opcji europejskich, a tzw. opcje amerykańskie można wykonać w dowolnej chwili aż do momentu wygaśnięcia.
Opcja jest umową, w której występują dwie strony: wystawiający
opcję (writer) i posiadacz opcji (holder). Posiadacz
opcji dysponuje prawem, za które musi zapłacić wystawiającemu. Cena
opcji, nazywana premią (option premium, option price)
jest ceną rynkową, zmieniającą się w czasie. Dla wielu inwestowanie
w opcje jest formą zabezpieczenia przed niekorzystnym ruchem cen,
a więc jest swoistą polisą ubezpieczeniową. Opcja kupna zabezpiecza
jej posiadacza, który chce w przyszłości kupić dany instrument
finansowy, przed skutkami wzrostu cen ponad ustalony poziom — cena
wykonania jest maksymalną ceną po jakiej posiadacz opcji kupna kupi
dany instrument finansowy. Opcja sprzedaży zabezpiecza jej
posiadacza przed spadkiem cen aktywa bazowego poniżej pewnego
poziomu; ten poziom to znów cena wykonania. Rozważmy opcje
europejskie. Zaczniemy od europejskiej opcji kupna, czyli opcji
dającej prawo do zakupu aktywa w chwili ![]() za ustaloną z góry cenę
za ustaloną z góry cenę
![]() . Niech
. Niech ![]() oznacza cenę aktywa w chwili
oznacza cenę aktywa w chwili ![]() . Jeśli
. Jeśli
![]() , to w chwili
, to w chwili ![]() posiadacz europejskiej opcji kupna
realizuje ją i otrzymuje
posiadacz europejskiej opcji kupna
realizuje ją i otrzymuje ![]() , a gdy
, a gdy ![]() , to nic nie
robi. W rezultacie otrzymuje wypłatę (payoff), którą można
zapisać w postaci:
, to nic nie
robi. W rezultacie otrzymuje wypłatę (payoff), którą można
zapisać w postaci:
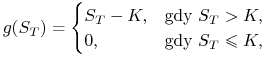 |
(1.1) |
czyli
| (1.2) |
Rozumując analogicznie otrzymujemy wzór opisujący wypłatę dla posiadacza europejskiej opcji sprzedaży:
| (1.3) |
Stąd widać, że wypłaty dla europejskich opcji kupna i sprzedaży spełniają prostą, acz pożyteczną równość:
| (1.4) |
Tożsamość ta przyda nam się przy obliczaniu cen opcji. Wiemy, ile
można uzyskać posiadając opcje europejskie. Powstaje pytanie, ile
powinniśmy zapłacić za opcje? W dalszej części spróbujemy
odpowiedzieć na pytanie, czy można wycenić dowolną wypłatę w chwili
![]() . Jeśli tak, to w jaki sposób i jaka powinna być cena? Gdy
ograniczymy się do opcji, powstaje problem: czy można wycenić opcję,
a jeśli tak, to za ile należy sprzedawać taki kontrakt? Zatem
. Jeśli tak, to w jaki sposób i jaka powinna być cena? Gdy
ograniczymy się do opcji, powstaje problem: czy można wycenić opcję,
a jeśli tak, to za ile należy sprzedawać taki kontrakt? Zatem
-
Ile powinien nabywca zapłacić za opcję? Innymi słowy, ile powinien kosztować w chwili
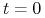 instrument dający losową wypłatę
instrument dający losową wypłatę
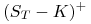 w chwili
w chwili 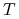 . Jest to problem wyceny opcji.
. Jest to problem wyceny opcji. -
Jak wystawca opcji może zabezpieczyć się przed losową stratą w chwili
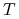 , którą by poniósł nie podejmując żadnych działań po
sprzedaży opcji? Innymi słowy, w jaki sposób wystawca opcji
powinien wygenerować wielkość
, którą by poniósł nie podejmując żadnych działań po
sprzedaży opcji? Innymi słowy, w jaki sposób wystawca opcji
powinien wygenerować wielkość 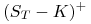 w chwili
w chwili 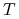 ,
dysponując zapłatą za opcję? Zagadnienie to możemy określić jako
problem zabezpieczenia opcji (hedging).
,
dysponując zapłatą za opcję? Zagadnienie to możemy określić jako
problem zabezpieczenia opcji (hedging).
W dalszej części omówimy także opcje o innych wypłatach i innych możliwych momentach wypłat tzw. opcje egzotyczne.
1.4. Rynek doskonały
Przyjmujemy założenie, obowiązujące w całym cyklu wykładów, że rynek, na którym chcemy wycenić ten kontrakt jest rynkiem idealnym (doskonałym), czyli:
-
oprocentowanie kredytów i depozytów bankowych jest jednakowe (założenie to nieźle opisuje sytuację dużych dealerów),
-
inwestorzy nie ponoszą żadnych kosztów, tj. kosztów transakcji, kosztów prowizji, nie płacą podatków, itp.,
-
nie ma ograniczeń w dostępie do kredytów, wysokość kredytów udzielanych pojedynczemu inwestorowi jest nieograniczona,
-
wszystkie operacje są realizowane natychmiast,
-
rynek jest płynny, tj. możemy kupić lub sprzedać dowolną liczbę aktywów,
-
dostęp do informacji jest taki sam dla wszystkich inwestorów,
-
uczestnicy rynku są małymi inwestorami, ich samodzielne działanie na rynku nie zmienia cen.
Są to minimalne założenia, przy których można modelować, w miarę prosto, zachowanie rynku. W rzeczywistości ceny obliczone w takim modelu są korygowane, by dopasować je do rynku. Na przykład, dodanie do wyliczonej ceny prowizji pokrywającej koszty powoduje ominięcie modelowego założenia, że inwestorzy nie ponoszą żadnych kosztów. Najbardziej kontrowersyjne jest założenie, mówiące że nie ma ograniczeń w dostępie do kredytów, ale przy opisie dopuszczalnych strategii inwestycyjnych (a więc sposobu postępowania inwestora) wyklucza się możliwość nieograniczonego kredytu nakładając ograniczenie na całkowitą wartość strategii. Konstruowane są też modele celowo opuszczające niektóre z założeń np. założenie, że dostęp do informacji jest taki sam dla wszystkich inwestorów, ale wymagają one zastosowania znacznie bardziej zaawansowanych metod analizy stochastycznej niż używane podczas tego wykładu.




