Zagadnienia
10. Wycena i zabezpieczenie w modelu Blacka-Scholesa
Zajmiemy się teraz wyceną i zabezpieczeniem wypłat w klasycznym
modelu Blacka-Scholesa ![]() , który jest wolny od arbitrażu (tw.
9.4).
, który jest wolny od arbitrażu (tw.
9.4).
10.1. Wycena ogólnej wypłaty
Wykażemy, że cena ![]() tzn. cena arbitrażowa w chwili
tzn. cena arbitrażowa w chwili ![]() wypłaty osiągalnej
wypłaty osiągalnej ![]() zdefiniowana jako wartość procesu
replikującego
zdefiniowana jako wartość procesu
replikującego ![]() jest dobrze określona i znajdziemy wzór
pozwalający liczyć te cenę.
jest dobrze określona i znajdziemy wzór
pozwalający liczyć te cenę.
Twierdzenie 10.1
Niech ![]() będzie wypłatą osiągalną
w
będzie wypłatą osiągalną
w ![]() Wtedy cena arbitrażowa
Wtedy cena arbitrażowa ![]() wypłaty
wypłaty ![]() jest dobrze określona i jest dana przez formułę wyceny neutralną
względem ryzyka:
jest dobrze określona i jest dana przez formułę wyceny neutralną
względem ryzyka:
| (10.1) |
Idea dowodu jest analogiczna do idei dowodu twierdzenia dla
czasu dyskretnego. Gdy ![]() replikuje wypłatę
replikuje wypłatę ![]() ,
to
,
to ![]() jest
jest ![]() –martyngałem, więc
–martyngałem, więc
Stąd wynika, że proces wartości portfela replikującego wypłatę ![]() jest wyznaczony jednoznacznie, gdyż dla
jest wyznaczony jednoznacznie, gdyż dla ![]() replikujących
replikujących ![]() zachodzi
zachodzi
czyli ![]() . Ponadto
. Ponadto
co kończy dowód.
∎Uwaga 10.1
a) Ponieważ ![]() jest
jest ![]() -ciałem zbiorów
-ciałem zbiorów ![]() -trywialnych,
zatem i
-trywialnych,
zatem i ![]() -trywialnych,
-trywialnych, ![]() , to cenę wypłaty
, to cenę wypłaty ![]() liczymy jako
wartość oczekiwaną przy mierze martyngałowej zdyskontowanej wypłaty:
liczymy jako
wartość oczekiwaną przy mierze martyngałowej zdyskontowanej wypłaty:
| (10.2) |
b) Jeśli ![]() jest wypłatą osiągalną
w
jest wypłatą osiągalną
w ![]() to mamy dobrze określoną cenę arbitrażową
to mamy dobrze określoną cenę arbitrażową ![]() w każdej chwili i
w każdej chwili i
więc zdyskontowana cena jest ![]() -martyngałem.
W konsekwencji możemy handlować tym instrumentem na rynku, gdyż
dołączenie tego instrumentu do rynku nie wprowadza arbitrażu (
-martyngałem.
W konsekwencji możemy handlować tym instrumentem na rynku, gdyż
dołączenie tego instrumentu do rynku nie wprowadza arbitrażu (![]() na rozszerzonym
rynku z procesem cen
na rozszerzonym
rynku z procesem cen ![]() jest miarą martyngałową).
jest miarą martyngałową).
Następne twierdzenie opisuje klasę wypłat replikowalnych.
Twierdzenie 10.2
W modelu
Blacka-Scholesa każda wypłata, która
jest całkowalna z kwadratem względem ![]() jest osiągalna.
jest osiągalna.
Trzeba wykazać, że dla każdego ![]() istnieje strategia dopuszczalna
istnieje strategia dopuszczalna
![]() replikująca wypłatę
replikująca wypłatę ![]() , czyli trzeba znaleźć
, czyli trzeba znaleźć ![]() , takie że
, takie że
Niech
| (10.3) |
Jest to martyngał całkowalny z kwadratem. Ponieważ ![]() jest
filtracją generowaną przez ruch Browna, więc z twierdzenia
o reprezentacji
istnieje proces adaptowany
jest
filtracją generowaną przez ruch Browna, więc z twierdzenia
o reprezentacji
istnieje proces adaptowany ![]() , taki że
, taki że
![]() i
i
| (10.4) |
Strategia zdefiniowana wzorami
| (10.5) |
ma kapitał początkowy
Jest strategią samofinansującą się, gdyż z (10.5),
(10.4), z tego, że ![]() i z
(9.11) mamy
i z
(9.11) mamy
i z lematu 9.2 strategia ![]() jest samofinansującą się.
Przy okazji udowodniliśmy, że
jest samofinansującą się.
Przy okazji udowodniliśmy, że ![]() , więc
, więc ![]() jest
jest ![]() -martyngałem, czyli
-martyngałem, czyli ![]() jest strategią dopuszczalną
tzn,
jest strategią dopuszczalną
tzn, ![]() oraz
oraz ![]() tzn.
tzn.
![]() .
.
Uwaga 10.2
a) W modelu Blacka-Scholesa cena wypłaty
całkowalnej z kwadratem względem ![]() jest równa
jest równa
| (10.6) |
Postać ![]() wynika natychmiast ze wzoru (10.1),
gdyż
wynika natychmiast ze wzoru (10.1),
gdyż ![]() .
.
b) Gdy uogólnimy definicję zupełności z rynku skończonego (na którym
każda wypłata jest ograniczona) przyjmując, że rynek bez możliwości
arbitrażu jest zupełny, gdy dla każdej ograniczonej wypłaty ![]() w chwili
w chwili ![]() istnieje strategia dopuszczalna replikująca wypłatę
istnieje strategia dopuszczalna replikująca wypłatę
![]() , to z Twierdzenia 10.2 wynika, że rynek jest zupełny
i ma miejsce sytuacja typowa dla tak zdefiniowanego rynku zupełnego:
klasa wypłat replikowalnych jest znacznie szersza niż klasa wypłat
ograniczonych.
, to z Twierdzenia 10.2 wynika, że rynek jest zupełny
i ma miejsce sytuacja typowa dla tak zdefiniowanego rynku zupełnego:
klasa wypłat replikowalnych jest znacznie szersza niż klasa wypłat
ograniczonych.
c) Dowodząc istnienia strategii dopuszczalnej
zabezpieczającej wypłatę użyliśmy twierdzenia o reprezentacji. Podkreśla to wagę
twierdzeń o reprezentacji do konstrukcji strategii zabezpieczających
(patrz też ćw. 4.6).
Twierdzenie 10.2 ma jedną wadę z punktu widzenia
zastosowań w praktyce, nie podaje explicite sposobu, w jaki
można replikować wypłatę, gdyż jego dowód korzysta z twierdzenia
o reprezentacji martyngału, a zwykle nie znamy jawnej postaci
procesu ![]() w przedstawieniu (10.4). Gdy uda nam się
znaleźć przedstawienie (10.4) dla którego znamy postać
w przedstawieniu (10.4). Gdy uda nam się
znaleźć przedstawienie (10.4) dla którego znamy postać ![]() ,
to wzory (10.5) zadają strategię replikującą.
,
to wzory (10.5) zadają strategię replikującą.
W sytuacji gdy wypłata zależy tylko od ceny końcowej ![]() , to można
podać portfel replikujący i jego wartość w jawnej postaci.
, to można
podać portfel replikujący i jego wartość w jawnej postaci.
Twierdzenie 10.3
Jeśli wypłata ![]() jest całkowalna
z kwadratem względem miary martyngałowej, to
jest całkowalna
z kwadratem względem miary martyngałowej, to ![]() dla
dla ![]() z funkcją
z funkcją ![]() daną w jawnej postaci:
daną w jawnej postaci:
| (10.7) |
Gdy ponadto ![]() dane wzorem (10.7) należy do klasy
dane wzorem (10.7) należy do klasy
![]() , to portfel
, to portfel ![]() zadany wzorem
zadany wzorem
| (10.8) | ||||
jest dopuszczalny i replikuje ![]() .
.
Gdy ![]() to ze wzorów (9.16) i
(10.6) mamy
to ze wzorów (9.16) i
(10.6) mamy
| (10.9) |
gdzie ![]() jest dane wzorem (10.7), gdyż
jest dane wzorem (10.7), gdyż ![]() jest
jest ![]() -mierzalne, a przyrost
-mierzalne, a przyrost ![]() jest
niezależny od
jest
niezależny od ![]() i ma rozkład normalny
i ma rozkład normalny ![]() .
.
Niech ![]() replikuje wypłatę
replikuje wypłatę ![]() i niech
i niech
Wtedy ![]() ,
, ![]() i
i
| (10.10) |
a zatem ![]() . Stąd, by zakończyć
dowód wystarczy znaleźć strategię replikującą
. Stąd, by zakończyć
dowód wystarczy znaleźć strategię replikującą ![]() mającą przedstawienie
mającą przedstawienie
z procesem ![]() zadanym w jawnej postaci.
zadanym w jawnej postaci.
Ze wzoru Itô dla procesu ![]() oraz (9.11) mamy
oraz (9.11) mamy
| (10.11) | |||||
gdzie
Ponieważ
![]() jest martyngałem (wzór (10.10)), to z (10.11) i z
tego, że martyngał ciągły o wahaniu ograniczonym jest stały
otrzymujemy
jest martyngałem (wzór (10.10)), to z (10.11) i z
tego, że martyngał ciągły o wahaniu ograniczonym jest stały
otrzymujemy ![]() , a stąd
, a stąd
| (10.12) |
Mając tę reprezentację definiujemy strategię:
Tak zdefiniowane ![]() spełnia
spełnia ![]() Stąd, z (10.1) i z lematu 9.2 wynika, że
Stąd, z (10.1) i z lematu 9.2 wynika, że ![]() jest strategią dopuszczalną.
Strategia
jest strategią dopuszczalną.
Strategia ![]() replikuje wypłatę
replikuje wypłatę ![]() , gdyż
, gdyż
Z (10.10) widać natychmiast, że strategię ![]() można
zapisać za pomocą funkcji
można
zapisać za pomocą funkcji ![]() :
:
Uwaga 10.3
Mając taką postać bogactwa strategii ![]() można się
spodziewać, że będziemy potrafili znaleźć jawną postać strategii
dopuszczalnej
można się
spodziewać, że będziemy potrafili znaleźć jawną postać strategii
dopuszczalnej ![]() replikującej wypłatę
replikującej wypłatę ![]() dla dużej
klasy funkcji
dla dużej
klasy funkcji ![]() takich, że
takich, że ![]() dane wzorem (10.7) należy
do klasy
dane wzorem (10.7) należy
do klasy ![]() .
W szczególności do tej klasy funkcji należą funkcje definiujące opcję kupna
i opcję sprzedaży.
.
W szczególności do tej klasy funkcji należą funkcje definiujące opcję kupna
i opcję sprzedaży.
Kontrakt forward na kupno akcji.
Zajmiemy się teraz kontraktem forward na kupno akcji na
rynku Blacka-Scholesa ![]() . Jak wiemy, wypłata
z takiego kontraktu jest zadana wzorem
. Jak wiemy, wypłata
z takiego kontraktu jest zadana wzorem ![]() , gdzie
, gdzie ![]() jest
ceną kontraktu forward w chwili 0. Wypłata jest osiągalna, gdyż jest
to kombinacja liniowa wypłat osiągalnych. Wiemy też, że
jest
ceną kontraktu forward w chwili 0. Wypłata jest osiągalna, gdyż jest
to kombinacja liniowa wypłat osiągalnych. Wiemy też, że
| (10.13) |
Stąd, ponieważ ![]() jest
jest ![]() -martyngałem, mamy
-martyngałem, mamy
Cena forward to taka wielkość ![]() , że cena
kontraktu w chwili 0 jest równa 0, wejście w kontrakt nic nie
kosztuje, czyli
, że cena
kontraktu w chwili 0 jest równa 0, wejście w kontrakt nic nie
kosztuje, czyli ![]() , tzn.
, tzn.
Znając ![]() znajdujemy wartość kontraktu w chwili
znajdujemy wartość kontraktu w chwili ![]() korzystając
z (10.13):
korzystając
z (10.13):
| (10.14) |
A jak wygląda portfel replikujący? Z (10.14) wiemy, że
![]() replikuje
replikuje ![]() gdy
gdy ![]() , czyli na przykład gdy
, czyli na przykład gdy
![]() ,
, ![]() . Ten portfel jest kombinacją portfeli
,,kup i trzymaj” (więc jest
samofinansujący się); należy kupić jedną akcję pożyczając z banku
kwotę na jej zakup i trzymać ten portfel bez zmian do momentu
realizacji kontraktu. W powyższych rozważaniach nie
wykorzystywaliśmy własności rynku specyficznych dla rynku
Blacka-Scholesa, więc to rozumowanie jest prawdziwe dla dowolnego
rynku z czasem ciągłym bez możliwości arbitrażu.
. Ten portfel jest kombinacją portfeli
,,kup i trzymaj” (więc jest
samofinansujący się); należy kupić jedną akcję pożyczając z banku
kwotę na jej zakup i trzymać ten portfel bez zmian do momentu
realizacji kontraktu. W powyższych rozważaniach nie
wykorzystywaliśmy własności rynku specyficznych dla rynku
Blacka-Scholesa, więc to rozumowanie jest prawdziwe dla dowolnego
rynku z czasem ciągłym bez możliwości arbitrażu.
10.2. Wycena opcji europejskich
Zajmiemy się teraz szczególnym przypadkiem funkcji wypłaty, a mianowicie opcjami kupna. Wyprowadzimy sławne wzory Blacka-Scholesa.
Twierdzenie 10.4
Cena arbitrażowa ![]() w chwili
w chwili
![]() europejskiej opcji kupna z ceną wykonania
europejskiej opcji kupna z ceną wykonania ![]() i momentem
wykonania
i momentem
wykonania ![]() na rynku Blacka-Scholesa jest równa:
na rynku Blacka-Scholesa jest równa:
| (10.15) |
dla ![]() , przy czym funkcja
, przy czym funkcja ![]() jest postaci
jest postaci
gdzie
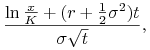 |
(10.16) | ||||
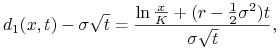 |
(10.17) |
a ![]() jest dystrybuantą rozkładu
jest dystrybuantą rozkładu ![]() . Ponadto,
dopuszczalna strategia replikująca ma postać
. Ponadto,
dopuszczalna strategia replikująca ma postać
| (10.18) |
Obliczymy ![]() zadane wzorem (10.7) dla funkcji
zadane wzorem (10.7) dla funkcji
![]() . Mamy
. Mamy
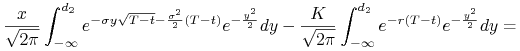 |
||||
gdzie
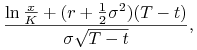 |
||||
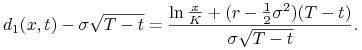 |
Korzystając z (10.1) otrzymujemy wzór (10.15). Postać (10.18) strategii dopuszczalnej replikującej wypłatę z opcji kupna otrzymujemy ze wzoru (10.1).
∎Uwaga 10.4
a) Z tego twierdzenia wynika, że
b) Portfel replikujący zawiera ![]() akcji, jest więc delta zabezpieczeniem
(por. wzór (5.8) dla modelu CRR), a ponieważ
akcji, jest więc delta zabezpieczeniem
(por. wzór (5.8) dla modelu CRR), a ponieważ ![]() , to portfel replikujący nie korzysta z
krótkiej sprzedaży.
, to portfel replikujący nie korzysta z
krótkiej sprzedaży.
Rozważymy teraz opcję sprzedaży. Ponieważ
więc
Stąd otrzymujemy formułę zgodności ceny opcji kupna i ceny opcji sprzedaży (parytet kupna-sprzedaży):
| (10.19) |
gdzie ![]() i
i ![]() oznaczają cenę w chwili
oznaczają cenę w chwili
![]() odpowiednio opcji kupna i opcji sprzedaży o cenie wykonania
odpowiednio opcji kupna i opcji sprzedaży o cenie wykonania ![]() i terminie wykonania
i terminie wykonania ![]() .
.
Wniosek 10.1
Cena arbitrażowa ![]() w chwili
w chwili
![]() europejskiej opcji sprzedaży z ceną wykonania
europejskiej opcji sprzedaży z ceną wykonania ![]() i momentem wykonania
i momentem wykonania ![]() równa się
równa się
| (10.21) |
gdzie ![]() jest zadane wzorem (10.20), a
jest zadane wzorem (10.20), a ![]() wzorami (10.16) i (10.17).
wzorami (10.16) i (10.17).
Portfel replikujący ma postać
Dowód wniosku pozostawimy jako zadanie (ćw. 10.4).
Przykład 10.1
Rozważmy europejską opcję kupna. Termin wygaśnięcia tej opcji
upływa za trzy miesiące. Bieżąca cena akcji wynosi 80, cena
wykonania 100. Stopa wolna od ryzyka ![]() ,
, ![]() .
Obliczymy cenę opcji kupna i wartość opcji sprzedaży z tą samą ceną
wykonania.
.
Obliczymy cenę opcji kupna i wartość opcji sprzedaży z tą samą ceną
wykonania.
Skorzystamy ze wzoru (10.15) i parytetu kupna-sprzedaży.
Wstawiamy dane: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() i otrzymujemy
i otrzymujemy ![]() oraz
oraz
![]() . Cenę
. Cenę ![]() można też otrzymać nie korzystając z parytetu, wyliczamy ją ze wzoru
(10.21).
można też otrzymać nie korzystając z parytetu, wyliczamy ją ze wzoru
(10.21).
Uwaga 10.5
Można udowodnić, że w modelu Blacka-Scholesa funkcja
![]() zadająca proces ceny arbitrażowej wypłaty
zadająca proces ceny arbitrażowej wypłaty ![]() jest
rozwiązaniem równania różniczkowego cząstkowego (równania
Blacka-Scholesa).
jest
rozwiązaniem równania różniczkowego cząstkowego (równania
Blacka-Scholesa).
| (10.22) |
![]() ,
, ![]() z warunkiem końcowym
z warunkiem końcowym ![]() dla
dla ![]() .
.
To wskazuje, że można się spodziewać, że wzory Blacka-Scholesa można otrzymać korzystając z równań różniczkowych cząstkowych. I tak rzeczywiście jest (patrz ćw. 10.11).
10.3. Analiza wrażliwości cen opcji
.
Warto zauważyć, że żadna z wielkości występujących w formułach
Blacka-Scholesa nie zależy od oczekiwanej stopy zwrotu inwestora
![]() (zatem od jego oceny ryzyka i od jego preferencji). Zależą
one natomiast od:
(zatem od jego oceny ryzyka i od jego preferencji). Zależą
one natomiast od:
– bieżącej ceny akcji ![]() ,
,
– ceny wykonania ![]() ,
,
– czasu ![]() pozostałego do realizacji opcji,
pozostałego do realizacji opcji,
– współczynnika zmienności ![]() ,
,
– stopy procentowej bez ryzyka ![]() .
.
Osoby zarządzające ryzykiem w instytucjach finansowych są
zainteresowane tym, jak bardzo mogą zmienić się ceny opcji w ich
portfelach inwestycyjnych, gdy zmienia się dokładnie jeden z powyższych
parametrów, gdyż takie zmiany mają wpływ na wartość całego portfela.
Zbadamy teraz pod tym kątem własności ceny opcji kupna. Dla prostoty
rozważymy cenę opcji w chwili zero, tj.
gdzie ![]() . Zbadamy, jak zmienia się cena opcji, gdy zmieniamy
jeden parametr, a pozostałe są zamrożone. Będziemy korzystali
z jawnej postaci wzoru na cenę opcji kupna (10.15) lub
z przedstawienia
. Zbadamy, jak zmienia się cena opcji, gdy zmieniamy
jeden parametr, a pozostałe są zamrożone. Będziemy korzystali
z jawnej postaci wzoru na cenę opcji kupna (10.15) lub
z przedstawienia
| (10.23) |
Teraz przeanalizujemy zależność funkcji ![]() od czynników
wymienionych powyżej. Okazuje się, że
od czynników
wymienionych powyżej. Okazuje się, że
-
a) Funkcja
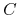 jest funkcją rosnącą jako funkcja zmiennej
jest funkcją rosnącą jako funkcja zmiennej 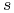 — bieżącej ceny
akcji.
— bieżącej ceny
akcji. -
b) Funkcja
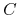 jest malejąca jako funkcja zmiennej
jest malejąca jako funkcja zmiennej 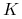 — ceny
wykonania.
— ceny
wykonania. -
c) Funkcja
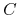 jest funkcją rosnącą jako funkcja czasu pozostałego do
realizacji opcji.
jest funkcją rosnącą jako funkcja czasu pozostałego do
realizacji opcji. -
d) Funkcja
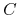 jest rosnąca jako funkcja zmiennej
jest rosnąca jako funkcja zmiennej 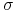 —
współczynnika zmienności.
—
współczynnika zmienności. -
e) Funkcja
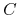 jest rosnąca jako funkcja zmiennej
jest rosnąca jako funkcja zmiennej 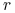 — stopy
procentowej bez ryzyka.
— stopy
procentowej bez ryzyka.
Ćwiczenie 10.1
Udowodnić powyższe stwierdzenia
-
a)
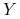 nie zależy od
nie zależy od 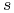 , więc prawa strona (10.23) rośnie
wtedy, gdy
, więc prawa strona (10.23) rośnie
wtedy, gdy 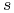 rośnie. Własność ta oznacza, że cena opcji rośnie gdy
wartość początkowa akcji rośnie.
rośnie. Własność ta oznacza, że cena opcji rośnie gdy
wartość początkowa akcji rośnie. -
b) Własność ta wynika z faktu, że prawa strona (10.23) maleje względem
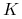 . Jest to intuicyjnie oczywiste, bo wartość wypłaty
z opcji
. Jest to intuicyjnie oczywiste, bo wartość wypłaty
z opcji 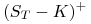 jest większa, gdy
jest większa, gdy 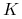 zmniejszymy.
zmniejszymy. -
c) Zaczniemy od uzasadnienia intuicyjnego. Jak wiemy na rynku dyskretnym cena europejskiej opcji kupna równa jest cenie amerykańskiej opcji kupna. Tego samego możemy oczekiwać dla modelu z czasem ciągłym, a dla opcji amerykańskiej wydłużenie czasu opcji zwiększa jej wartość (nabywca opcji ma więcej praw). Rachunek formalny — obliczamy pochodną:
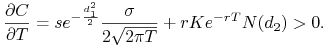
-
d) Nabywca opcji zyskuje, gdy cena opcji bardzo wzrośnie w momencie wykonania, natomiast nie ma znaczenia spadek ceny poniżej ceny wykonania
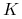 , bowiem i tak nabywca opcji nic wtedy nie dostaje.
Formalnie:
, bowiem i tak nabywca opcji nic wtedy nie dostaje.
Formalnie: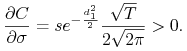
(10.24) -
e) Istotnie, wyrażenie pod znakiem całki w (10.23) rośnie, gdy
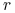 rośnie, bo odjemna nie zależy od
rośnie, bo odjemna nie zależy od 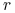 , a odjemnik maleje. Inne
uzasadnienie tego faktu wynika z dodatniości pochodnej
, a odjemnik maleje. Inne
uzasadnienie tego faktu wynika z dodatniości pochodnej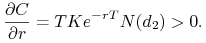
10.4. Szukanie współczynnika zmienności ceny akcji.
W praktyce,
by obliczyć cenę opcji musimy znać współczynnik zmienności ![]() .
Jest to wielkość rynkowa i trzeba ją znaleźć patrząc na zachowanie
rynku. W tym celu powszechnie stosowane są dwie metody:
.
Jest to wielkość rynkowa i trzeba ją znaleźć patrząc na zachowanie
rynku. W tym celu powszechnie stosowane są dwie metody:
a) metoda zmienności
historycznej (historic
volatility) — estymacja ![]() z danych z przeszłości,
z danych z przeszłości,
b) metoda zmienności implikowanej (implied volatility).
Omówimy je kolejno.
Ad a). Metoda ta opiera się na danych z rynku — danych
historycznych. Aby estymować ![]() obserwujemy ceny w ustalonych
okresach czasu o równej długości (np. codziennie, co tydzień itp.).
Oznaczmy:
obserwujemy ceny w ustalonych
okresach czasu o równej długości (np. codziennie, co tydzień itp.).
Oznaczmy:
![]() — liczba obserwacji; obserwacji dokonujemy w chwilach
— liczba obserwacji; obserwacji dokonujemy w chwilach ![]() , takich, że odstępy czasu pomiędzy obserwacjami są
równe,
, takich, że odstępy czasu pomiędzy obserwacjami są
równe,
![]() — długość przedziału czasu pomiędzy obserwacjami (liczona
w latach),
— długość przedziału czasu pomiędzy obserwacjami (liczona
w latach),
![]() — zaobserwowana cena akcji na końcu
— zaobserwowana cena akcji na końcu ![]() -tego przedziału
czasu
-tego przedziału
czasu ![]() .
.
Niech ![]() będzie teoretyczną ceną akcji na końcu
będzie teoretyczną ceną akcji na końcu ![]() -tego
przedziału, tj.
-tego
przedziału, tj. ![]() i niech
i niech
— są to tzw. logarytmiczne zwroty cen. Wtedy ![]() , czyli
, czyli ![]() jest ciągłą stopą zwrotu
w
jest ciągłą stopą zwrotu
w ![]() -tym przedziale (ale nie w skali roku). Ponieważ założyliśmy,
że rynek opisuje model Blacka-Scholesa, więc ze wzoru (9.5)
wynika, że
-tym przedziale (ale nie w skali roku). Ponieważ założyliśmy,
że rynek opisuje model Blacka-Scholesa, więc ze wzoru (9.5)
wynika, że ![]() są niezależnymi zmiennymi losowymi o jednakowym
rozkładzie normalnym z wariancją
są niezależnymi zmiennymi losowymi o jednakowym
rozkładzie normalnym z wariancją ![]() i wartością średnią
i wartością średnią
![]() zależną od preferencji inwestora
(rynku).
zależną od preferencji inwestora
(rynku).
Z rynku mamy obserwacje cen, czyli wielkości ![]() ,
a stąd możemy wyznaczyć wielkości
,
a stąd możemy wyznaczyć wielkości ![]() . Odchylenie
standardowe zmiennej losowej
. Odchylenie
standardowe zmiennej losowej ![]() jest równe
jest równe ![]() ,
a estymatorem odchylenia standardowego
,
a estymatorem odchylenia standardowego ![]() niezależnym od wartości
średniej jest statystyka
niezależnym od wartości
średniej jest statystyka
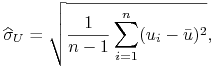 |
gdzie ![]() . Podkreślmy, że ten
estymator nie zależy od wartości średniej. Zatem
. Podkreślmy, że ten
estymator nie zależy od wartości średniej. Zatem
![]() estymuje
estymuje ![]() . Stąd
współczynnik zmienności
. Stąd
współczynnik zmienności ![]() jest estymowany przez
jest estymowany przez ![]() Błąd
standardowy tej estymacji wynosi w przybliżeniu
Błąd
standardowy tej estymacji wynosi w przybliżeniu ![]() .
.
Wybranie właściwego ![]() nie jest łatwe. Im większe
nie jest łatwe. Im większe ![]() , tym lepszy
estymator, ale używamy starszych danych, a jak powszechnie wiadomo,
model Blacka-Scholesa w miarę poprawnie
opisuje rynek dla krótkich okresów czasu. Z badań empirycznych
wynika, że dla długich okresów czasu
, tym lepszy
estymator, ale używamy starszych danych, a jak powszechnie wiadomo,
model Blacka-Scholesa w miarę poprawnie
opisuje rynek dla krótkich okresów czasu. Z badań empirycznych
wynika, że dla długich okresów czasu ![]() zmienia się w czasie
(nie jest stacjonarne). Zawsze szacowanie przyszłej wartości
zmienia się w czasie
(nie jest stacjonarne). Zawsze szacowanie przyszłej wartości
![]() na podstawie przeszłości obarczone jest błędem. Należy wybrać taki
okres czasu, by estymator miał dobre
własności i jednocześnie na tyle krótki, że założenie, iż rynek jest
opisany przez model Blacka-Scholesa można zaakceptować. Na ogół
przyjęcie długości okresu czasu używanego do estymacji jest
dyktowane doświadczeniem osoby wykonującej takie szacowania.
Podkreślmy jeszcze raz, że stosując metodę historyczną zakładamy, że
parametr
na podstawie przeszłości obarczone jest błędem. Należy wybrać taki
okres czasu, by estymator miał dobre
własności i jednocześnie na tyle krótki, że założenie, iż rynek jest
opisany przez model Blacka-Scholesa można zaakceptować. Na ogół
przyjęcie długości okresu czasu używanego do estymacji jest
dyktowane doświadczeniem osoby wykonującej takie szacowania.
Podkreślmy jeszcze raz, że stosując metodę historyczną zakładamy, że
parametr ![]() nie zmieni się w czasie, a więc metoda ta nie
uwzględnia możliwych zmian wielkości parametru
nie zmieni się w czasie, a więc metoda ta nie
uwzględnia możliwych zmian wielkości parametru ![]() (czyli tego,
że po pewnym czasie rynek opisuje model Blacka-Scholesa z inną
zmiennością).
(czyli tego,
że po pewnym czasie rynek opisuje model Blacka-Scholesa z inną
zmiennością).
Ad b). Metoda zmienności implikowanej opiera się na przekonaniu, że zmienność jest zdeterminowana przez rynek.
Z (10.24) wynika, że cena opcji jest rosnącą funkcją
parametru ![]() , gdy pozostałe czynniki są stałe. Zatem znając
z rynku wielkości:
, gdy pozostałe czynniki są stałe. Zatem znając
z rynku wielkości: ![]() (cena akcji),
(cena akcji), ![]() ,
, ![]() ,
, ![]() i
i ![]() (cena opcji obserwowana na
rynku) możemy znaleźć tę wartość
(cena opcji obserwowana na
rynku) możemy znaleźć tę wartość ![]() , przy której cena
teoretyczna opcji jest równa cenie rynkowej, czyli tę wartość
, przy której cena
teoretyczna opcji jest równa cenie rynkowej, czyli tę wartość
![]() dla której
dla której ![]() . Dokładniej, zakładamy, że
. Dokładniej, zakładamy, że
![]() są ustalone i znane. Jak wiemy
są ustalone i znane. Jak wiemy
Definicja 10.1
Zmiennością implikowaną ![]() nazywa
się tę dodatnią wielkość
nazywa
się tę dodatnią wielkość ![]() , dla której
, dla której
| (10.25) |
Inaczej mówiąc, ![]() jest tą wielkością odchylenia
standardowego stopy zwrotu z akcji, która przy zastosowaniu wzoru
Blacka-Scholesa daje cenę teoretyczną
opcji równą cenie opcji na rynku. Gdy
jest tą wielkością odchylenia
standardowego stopy zwrotu z akcji, która przy zastosowaniu wzoru
Blacka-Scholesa daje cenę teoretyczną
opcji równą cenie opcji na rynku. Gdy ![]() , to
istnieje dokładnie jedno dodatnie rozwiązanie (10.25), co
wynika z (10.24). Zmienność
implikowana
, to
istnieje dokładnie jedno dodatnie rozwiązanie (10.25), co
wynika z (10.24). Zmienność
implikowana ![]() jest
rozwiązaniem tego nieliniowego równania (10.25). Rozważamy
to w obecnej chwili
jest
rozwiązaniem tego nieliniowego równania (10.25). Rozważamy
to w obecnej chwili ![]() , znamy
, znamy ![]() , więc bez straty ogólności
możemy założyć, że
, więc bez straty ogólności
możemy założyć, że ![]() .
.
Gdy ustalimy czas do wygaśnięcia opcji ![]() i gdy rynek jest opisany
przez model Blacka-Scholesa to
i gdy rynek jest opisany
przez model Blacka-Scholesa to ![]() powinno być stałe
i równe
powinno być stałe
i równe ![]() z modelu. W rzeczywistości, gdy używa się opcji
o różnych cenach wykonania dla tej samej akcji, czyli rozpatrujemy
funkcję
z modelu. W rzeczywistości, gdy używa się opcji
o różnych cenach wykonania dla tej samej akcji, czyli rozpatrujemy
funkcję ![]() (implikowana krzywa zmienności), to
(implikowana krzywa zmienności), to
![]() jako funkcja
jako funkcja ![]() nie jest stałą, ma miejsce tzw.
efekt uśmiechu zmienności
(implikowana krzywa zmienności jest wypukła i ma minimum).
W
praktyce otrzymuje się różne kształty wykresu funkcji.
Stąd jedną z metod znajdowania zmienności implikowanej
dla rynku jest branie odpowiednio ważonej średniej ze współczynników
zmienności implikowanej obliczanych dla różnych opcji, przy czym
najlepiej brać te opcje, których cena jest bardziej czuła na zmiany
parametru
nie jest stałą, ma miejsce tzw.
efekt uśmiechu zmienności
(implikowana krzywa zmienności jest wypukła i ma minimum).
W
praktyce otrzymuje się różne kształty wykresu funkcji.
Stąd jedną z metod znajdowania zmienności implikowanej
dla rynku jest branie odpowiednio ważonej średniej ze współczynników
zmienności implikowanej obliczanych dla różnych opcji, przy czym
najlepiej brać te opcje, których cena jest bardziej czuła na zmiany
parametru ![]() . Inną metodą jest wybór
. Inną metodą jest wybór ![]() , w taki
sposób by ceny teoretyczne
, w taki
sposób by ceny teoretyczne ![]() wybranych opcji były jak najbliższe
cen rynkowych tych opcji, tj. by
wybranych opcji były jak najbliższe
cen rynkowych tych opcji, tj. by
dla ![]() . Zwykle wybiera się kryterium metody
najmniejszych kwadratów, by ocenić, co to znaczy najbliższe, tj.
rozwiązuje się problem minimalizacji
. Zwykle wybiera się kryterium metody
najmniejszych kwadratów, by ocenić, co to znaczy najbliższe, tj.
rozwiązuje się problem minimalizacji
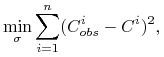 |
gdzie ![]() ,
, ![]() i jako
i jako ![]() przyjmuje się
przyjmuje się ![]() rozwiązujące ten problem. Jeszcze innym wyjściem jest taka
modyfikacja modelu, w której parametr
rozwiązujące ten problem. Jeszcze innym wyjściem jest taka
modyfikacja modelu, w której parametr ![]() przestaje być stały
(są to modele stochastycznej zmienności).
przestaje być stały
(są to modele stochastycznej zmienności).
Uwaga 10.6
Z parytetu (który także wynika z argumentów arbitrażowych,
a nie z konkretnego modelu) można oczekiwać, że zmienność
implikowana wyznaczona za pomocą opcji sprzedaży (odpowiednik wzoru
(10.25) zastosowany do ![]() i
i ![]() ) będzie równa zmienności implikowanej wyznaczonej
za pomocą opcji kupna z tymi samymi
) będzie równa zmienności implikowanej wyznaczonej
za pomocą opcji kupna z tymi samymi ![]() (patrz ćw. 10.12).
(patrz ćw. 10.12).
Uwaga 10.7
Z (10.19) wynika, że jeżeli rynek wycenia aktywa
zgodnie z modelem Blacka-Scholesa i cena opcji kupna na rynku
rośnie, to i cena opcji sprzedaży (oczywiście dla tych samych ![]() ) rośnie.
) rośnie.
Z punktu widzenia praktyka można zapytać: po co szukać ![]() ,
przecież na rynku mamy ceny opcji kupna i sprzedaży zadane przez
prawo popytu i podaży na rynku. Do handlowania tymi opcjami nie
trzeba znać
,
przecież na rynku mamy ceny opcji kupna i sprzedaży zadane przez
prawo popytu i podaży na rynku. Do handlowania tymi opcjami nie
trzeba znać ![]() . To prawda, ale mając
. To prawda, ale mając ![]() mamy dobrze
opisany model cen i model rynku. Wtedy potrafimy wyceniać opcje
egzotyczne i opcje tworzone na
żądanie, których ceny nie są
dostępne na rynku w każdej chwili, gdyż nie są to instrumenty płynne
(dokładniej, możemy wtedy zastosować procedury, najczęściej
przybliżone, konstruowane w celu wyceny opcji
egzotycznych, patrz
11.2). Ponadto znajomość współczynnika zmienności
mamy dobrze
opisany model cen i model rynku. Wtedy potrafimy wyceniać opcje
egzotyczne i opcje tworzone na
żądanie, których ceny nie są
dostępne na rynku w każdej chwili, gdyż nie są to instrumenty płynne
(dokładniej, możemy wtedy zastosować procedury, najczęściej
przybliżone, konstruowane w celu wyceny opcji
egzotycznych, patrz
11.2). Ponadto znajomość współczynnika zmienności ![]() jest
niezbędna do konstruowania portfeli zabezpieczających.
jest
niezbędna do konstruowania portfeli zabezpieczających.
Warto podkreślić, że procedura znajdowania wielkości implikowanych była możliwa, gdyż znaliśmy jawny wzór na ceny opcji i mogliśmy go odwrócić. Stąd widać jak ważne są w tym modelu rynku który konstruujemy jawne wzory na ceny instrumentów którymi handlujemy.
10.5. Opcje na instrument bazowy płacący dywidendy. Opcje walutowe
Rozważymy teraz opcje na akcje płacące dywidendy (wzór Mertona z roku 1973). Zaczniemy od rozumowania nieformalnego.
Niech akcja o cenie równej ![]() płaci dywidendę
z ciągłą stopą
płaci dywidendę
z ciągłą stopą ![]() w skali roku, proporcjonalną do poziomu ceny
(sensowność takiego spojrzenia uzasadnili Samuelson [Sam] oraz
Samuelson i Merton
[Sam-M],
w skali roku, proporcjonalną do poziomu ceny
(sensowność takiego spojrzenia uzasadnili Samuelson [Sam] oraz
Samuelson i Merton
[Sam-M], ![]() jest stałą. Wypłata dywidendy powoduje spadek ceny
akcji (część wartości idzie na dywidendę). Zatem jeśli cena akcji
wzrośnie z
jest stałą. Wypłata dywidendy powoduje spadek ceny
akcji (część wartości idzie na dywidendę). Zatem jeśli cena akcji
wzrośnie z ![]() do
do ![]() , to gdyby nie było dywidendy, cena akcji
wzrosłaby w okresie od
, to gdyby nie było dywidendy, cena akcji
wzrosłaby w okresie od ![]() do
do ![]() do wielkości
do wielkości ![]() .
Stąd cena opcji europejskiej na akcję o wartości
.
Stąd cena opcji europejskiej na akcję o wartości ![]() w chwili
w chwili ![]() płacącą dywidendę
płacącą dywidendę ![]() jest równa cenie opcji na akcję nie płacącą
dywidendy o cenie w chwili
jest równa cenie opcji na akcję nie płacącą
dywidendy o cenie w chwili ![]() równej
równej ![]() , gdyż obie
opcje wypłacają tyle samo w momencie
, gdyż obie
opcje wypłacają tyle samo w momencie ![]() (korzystamy z prawa jednej
ceny). Możemy zatem użyć wzorów
Blacka-Scholesa zmniejszając cenę akcji
do
(korzystamy z prawa jednej
ceny). Możemy zatem użyć wzorów
Blacka-Scholesa zmniejszając cenę akcji
do ![]() i otrzymane w ten sposób wzory będą dawały
ceny opcji na akcje płacące dywidendy.
i otrzymane w ten sposób wzory będą dawały
ceny opcji na akcje płacące dywidendy.
Wyprowadzimy teraz te wzory formalnie. Rozpatrzmy rynek, na którym jest rachunek bankowy i akcja płacąca dywidendy o cenie zadanej, jak zawsze w modelu Blacka-Scholesa, wzorem
| (10.26) |
Z założenia, proces wartości
dywidendy ![]() jest określony
przez
jest określony
przez
ale proces ![]() nie jest aktywem, którym handlujemy, zatem trzeba
dywidendę zainwestować w rynek: kupić akcje lub umieścić ją na
rachunku bankowym. Biorąc pod uwagę dywidendę mówimy, że strategia
nie jest aktywem, którym handlujemy, zatem trzeba
dywidendę zainwestować w rynek: kupić akcje lub umieścić ją na
rachunku bankowym. Biorąc pod uwagę dywidendę mówimy, że strategia
![]() jest samofinansującą się, gdy proces
bogactwa
jest samofinansującą się, gdy proces
bogactwa
spełnia równanie:
| (10.27) |
a więc (z postaci ![]() i
i ![]() ) otrzymujemy
) otrzymujemy
| (10.28) |
Rozpatrzmy proces ![]() (intuicyjnie
(intuicyjnie ![]() jest procesem ceny akcji zwiększonym o stratę wynikającą z wypłaty
dywidendy z ciągłą stopą
jest procesem ceny akcji zwiększonym o stratę wynikającą z wypłaty
dywidendy z ciągłą stopą ![]() ). Ze wzoru na całkowanie przez części
otrzymujemy, że
). Ze wzoru na całkowanie przez części
otrzymujemy, że ![]() spełnia
spełnia
| (10.29) |
Stąd ![]() , czyli zdyskontowany proces
, czyli zdyskontowany proces
![]() spełnia
spełnia
| (10.30) |
Zmieniając miarę na równoważną miarę probabilistyczną ![]() o gęstości
o gęstości
| (10.31) |
i korzystając z tego, że
jest procesem Wienera na ![]() względem
względem ![]() otrzymujemy z (10.30):
otrzymujemy z (10.30):
| (10.32) |
Zbadajmy teraz dynamikę procesu wartości
portfela ![]() spełniającego
(10.28). Ze wzoru Itô i z
(10.29) mamy
spełniającego
(10.28). Ze wzoru Itô i z
(10.29) mamy
| (10.33) |
Dalej ze wzoru na całkowanie przez części, z (10.33) i (10.32) mamy
| (10.34) |
więc proces ![]() jest
jest ![]() -lokalnym martyngałem. Dlatego
na rynku, na którym handlujemy akcją płacącą dywidendy oraz istnieje
rachunek bankowy można w standardowy sposób zdefiniować zbiór
strategii dopuszczalnych
-lokalnym martyngałem. Dlatego
na rynku, na którym handlujemy akcją płacącą dywidendy oraz istnieje
rachunek bankowy można w standardowy sposób zdefiniować zbiór
strategii dopuszczalnych ![]() , arbitraż i model rynku bez
możliwości arbitrażu
, arbitraż i model rynku bez
możliwości arbitrażu ![]() . Powtarzając poprzednie rozumowania
otrzymujemy wzory na ceny opcji kupna
na tym rynku:
. Powtarzając poprzednie rozumowania
otrzymujemy wzory na ceny opcji kupna
na tym rynku:
A ponieważ ![]() jest
jest ![]() -martyngałem, więc możemy powtórzyć
rozumowanie przeprowadzone dla rynku Blacka-Scholesa albo starannie
przyglądając się tamtym rachunkom zobaczyć, że
-martyngałem, więc możemy powtórzyć
rozumowanie przeprowadzone dla rynku Blacka-Scholesa albo starannie
przyglądając się tamtym rachunkom zobaczyć, że
gdzie ![]() jest wzorem dającym wycenę opcji kupna w modelu
Blacka-Scholesa. W ten sposób otrzymujemy wzory
Mertona:
jest wzorem dającym wycenę opcji kupna w modelu
Blacka-Scholesa. W ten sposób otrzymujemy wzory
Mertona:
Twierdzenie 10.5
Cena arbitrażowa ![]() w chwili
w chwili ![]() europejskiej opcji kupna na akcję płacącą dywidendę z ciągłą
stopą
europejskiej opcji kupna na akcję płacącą dywidendę z ciągłą
stopą ![]() w skali roku proporcjonalną do poziomu ceny jest równa:
w skali roku proporcjonalną do poziomu ceny jest równa:
| (10.35) | |||||
| (10.36) |
gdzie ![]() jest ceną wykonania,
jest ceną wykonania, ![]() momentem wykonania opcji,
momentem wykonania opcji,
| (10.37) | |||||
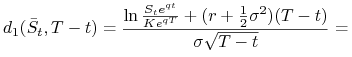 |
|||||
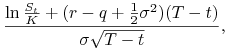 |
|||||
| (10.38) |
Podkreślmy jeszcze raz, że wzory wyprowadziliśmy przy założeniu, że
wypłacana dywidenda jest stała. Gdy ![]() zmienia się, to jako
przybliżenie
zmienia się, to jako
przybliżenie ![]() należy wziąć średnią z rocznych stóp. Stopa
dywidendy
należy wziąć średnią z rocznych stóp. Stopa
dywidendy ![]() , którą można otrzymać z danych historycznych, zmienia
się nieznacznie w ciągu kwartału, zatem dla opcji o krótkim terminie
zapadalności można
zakładać, że stopa
, którą można otrzymać z danych historycznych, zmienia
się nieznacznie w ciągu kwartału, zatem dla opcji o krótkim terminie
zapadalności można
zakładać, że stopa ![]() jest stała. W rzeczywistości założenie, że
pojedyncza spółka płaci dywidendę zgodnie z modelem
Samuelsona jest
nierealistyczne. Ale okazuje się, że ten model można stosować
z powodzeniem do indeksów giełdowych. W tym celu zakładamy, że
indeks jest opisywany przez geometryczny proces Wienera.
Teoretycznie tak nie musi być, bo jest to średnia ważona procesów
cen, które są geometrycznymi procesami Wienera. Ale dla zastosowań
praktycznych taki model jest sensowny i dobrze przybliża
rzeczywistość.
jest stała. W rzeczywistości założenie, że
pojedyncza spółka płaci dywidendę zgodnie z modelem
Samuelsona jest
nierealistyczne. Ale okazuje się, że ten model można stosować
z powodzeniem do indeksów giełdowych. W tym celu zakładamy, że
indeks jest opisywany przez geometryczny proces Wienera.
Teoretycznie tak nie musi być, bo jest to średnia ważona procesów
cen, które są geometrycznymi procesami Wienera. Ale dla zastosowań
praktycznych taki model jest sensowny i dobrze przybliża
rzeczywistość.
Przykład 10.2
Europejska opcja sprzedaży i kupna na indeks S&P500 ma termin
zapadalności 1 miesiąc. Obecna wartość indeksu wynosi 200, cena
wykonania 210, stopa procentowa bez ryzyka jest równa 5% p.a.,
a zmienność indeksu 10% p.a. średnia dywidenda wynosi 3% p.a. Ceny
opcji ![]() obliczamy korzystając ze wzorów: (10.35)
i (10.35) dla danych:
obliczamy korzystając ze wzorów: (10.35)
i (10.35) dla danych: ![]() miesiąc
miesiąc ![]() i otrzymujemy:
i otrzymujemy: ![]() ,
, ![]() .
.
Opcje walutowe. Wzory Mertona
(10.35) i (10.36) można zastosować do wyceny opcji
walutowych, czyli opcji wystawianych na walutę
zagraniczną a wycenianych w walucie krajowej. Cena waluty
zagranicznej ![]() jest po prostu
kursem wymiany i jest zadana wzorem (9.2) z odpowiednio
dobranymi
jest po prostu
kursem wymiany i jest zadana wzorem (9.2) z odpowiednio
dobranymi ![]() ,
, ![]() . Posiadacz waluty zagranicznej otrzymuje
dywidendę
. Posiadacz waluty zagranicznej otrzymuje
dywidendę ![]() , która jest stopą procentową bez ryzyka
, która jest stopą procentową bez ryzyka ![]() dla tej
waluty. Zatem można zastosować wzory (10.35)
i (10.36) dla
dla tej
waluty. Zatem można zastosować wzory (10.35)
i (10.36) dla ![]() . Jak łatwo zauważyć
(patrz ćw. 10.13), cena kontraktu forward w chwili
. Jak łatwo zauważyć
(patrz ćw. 10.13), cena kontraktu forward w chwili
![]() na dostawę jednostki waluty zagranicznej w momencie
na dostawę jednostki waluty zagranicznej w momencie ![]() przy
kursie wymiany
przy
kursie wymiany ![]() wynosi:
wynosi:
| (10.39) |
Korzystając z tego otrzymujemy wzory Garmana-Kohlhagena, niezależnie otrzymane przez Bigera i Hulla (1983), na ceny (w walucie krajowej) opcji kupna i sprzedaży wystawianych na walutę obcą:
gdzie
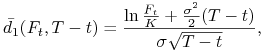 |
||||
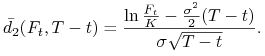 |
W standardowy sposób można otrzymać cenę w walucie krajowej dowolnej
wypłaty ![]() na rynku zagranicznym. Oczywiście jest ona równa cenie
tej wypłaty w walucie zagranicznej (patrz ćw. 10.14).
na rynku zagranicznym. Oczywiście jest ona równa cenie
tej wypłaty w walucie zagranicznej (patrz ćw. 10.14).
Jak wiemy ze wzoru (10.39) cena forward w chwili ![]() na
dostawę jednostki waluty zagranicznej w momencie
na
dostawę jednostki waluty zagranicznej w momencie ![]() przy kursie
wymiany
przy kursie
wymiany ![]() wynosi:
wynosi:
gdzie ![]() jest miarą martyngałową dla
jest miarą martyngałową dla ![]() . Gdy wymieniamy walutę
zagraniczną na krajową, to kurs wymiany jest procesem
. Gdy wymieniamy walutę
zagraniczną na krajową, to kurs wymiany jest procesem ![]() i jego dynamika przy jego mierze martyngałowej
i jego dynamika przy jego mierze martyngałowej ![]() (czyli
przy mierze martyngałowej na rynku zagranicznym) jest równa
(czyli
przy mierze martyngałowej na rynku zagranicznym) jest równa
| (10.40) |
gdzie ![]() jest procesem Wienera przy mierze martyngałowej
jest procesem Wienera przy mierze martyngałowej
![]() . Zatem cena forward jednostki waluty krajowej (w
jednostkach waluty zagranicznej) jest równa
. Zatem cena forward jednostki waluty krajowej (w
jednostkach waluty zagranicznej) jest równa
a stąd wynika, że ceny forward są, jak należało oczekiwać na rynku bez możliwości arbitrażu, zgodne.
| (10.41) |
Ale cena forward na dostawę jednej jednostki waluty zagranicznej
w chwili ![]() nie jest na ogół nieobciążonym estymatorem wartości
kursu wymiany w chwili
nie jest na ogół nieobciążonym estymatorem wartości
kursu wymiany w chwili ![]() . Jest to tzw. paradoks Siegela (patrz
ćw. 10.15).
. Jest to tzw. paradoks Siegela (patrz
ćw. 10.15).
10.6. Zagadnienia i zadania na ćwiczenia
Ćwiczenie 10.2
Czy na klasycznym rynku Blacka-Scholesa cena opcji kupna równa 40 i opcji sprzedaży równa 30 o terminie zapadalności 1 rok z ceną wykonania 38 przy obecnej cenie waloru 45 i współczynniku zmienności równym 20% stwarzają możliwość arbitrażu? Stopa procentowa bez ryzyka wynosi 10% dla wszystkich terminów do jednego roku. W przypadku istnienia arbitrażu, opisać go.
Ponieważ ![]() , więc nie zachodzi
parytet, zatem istnieje arbitraż, np. sprzedajemy krótko akcję,
sprzedajemy opcję sprzedaży i kupujemy opcję kupna.
, więc nie zachodzi
parytet, zatem istnieje arbitraż, np. sprzedajemy krótko akcję,
sprzedajemy opcję sprzedaży i kupujemy opcję kupna.
Ćwiczenie 10.3
Zbadać zachowanie ceny opcji europejskiej gdy ![]() .
.
Gdy ![]() , to
, to ![]() ,
, ![]() gdy
gdy
![]() oraz
oraz
| (10.42) |
Gdy ![]() , to
, to ![]() i zachodzi (10.42).
i zachodzi (10.42).
Gdy ![]() , to
, to ![]() ,
, ![]() i
i ![]() .
.
Warto zauważyć, że gdy ![]() (
(![]() i cena rośnie
zgodnie ze stopą bez ryzyka), to cena europejskiej opcji kupna jest
równa
i cena rośnie
zgodnie ze stopą bez ryzyka), to cena europejskiej opcji kupna jest
równa
i jest jednocześnie równa wielkości otrzymanej z przejścia
granicznego (![]() we wzorach
Blacka-Scholesa.
we wzorach
Blacka-Scholesa.
Ćwiczenie 10.4
Udowodnić wniosek 10.1, dający cenę europejskiej opcji sprzedaży.
Ćwiczenie 10.5
Znaleźć strategię dopuszczalną replikującą wypłatę z europejskiej opcji sprzedaży.
Ćwiczenie 10.6
Udowodnić, że cena europejskiej opcji:
a) kupna,
b) sprzedaży
jest funkcją wypukłą i spełnia warunek Lipschitza jako funkcja ceny wykonania.
Ćwiczenie 10.7
Udowodnić, że cena europejskiej opcji:
a) kupna,
b) sprzedaży
jest funkcją wypukłą i spełnia warunek Lipschitza jako funkcja bieżącej ceny akcji.
Ćwiczenie 10.8
Znaleźć cenę wypłaty
gdzie ![]() ,
, ![]() i
i ![]() są stałymi.
są stałymi.
Patrz przykł. 4.1.
Ćwiczenie 10.9
Powiemy, że ![]() reprezentuje wartość instrumentu, którym handluje
się na rynku Blacka-Scholesa, gdy
reprezentuje wartość instrumentu, którym handluje
się na rynku Blacka-Scholesa, gdy ![]() jest
jest
![]() -martyngałem (gdzie
-martyngałem (gdzie ![]() jest miarą martyngałową dla
jest miarą martyngałową dla ![]() ).
).
a) Wykazać, że ![]() dla
dla ![]() nie reprezentuje
instrumentu, którym się handluje.
nie reprezentuje
instrumentu, którym się handluje.
b) Dla jakiego ![]() proces
proces ![]() reprezentuje wartość
instrumentu, którym się handluje?
reprezentuje wartość
instrumentu, którym się handluje?
Ćwiczenie 10.10
Udowodnić, że w modelu Blacka-Scholesa cena wypłaty postaci
![]() , gdzie
, gdzie ![]() ,
, ![]() jest równa
jest równa
| (10.43) |
gdzie ![]() jest ceną arbitrażową europejskiej opcji kupna akcji
o cenie
jest ceną arbitrażową europejskiej opcji kupna akcji
o cenie ![]() z terminem wykonania
z terminem wykonania ![]() i ceną wykonania
i ceną wykonania ![]() .
.
Ćwiczenie 10.11
Udowodnić, że w modelu Blacka-Scholesa funkcja ![]() zadająca proces
ceny opcji kupna
zadająca proces
ceny opcji kupna ![]() jest rozwiązaniem równania
różniczkowego cząstkowego (równania Blacka-Scholesa).
jest rozwiązaniem równania
różniczkowego cząstkowego (równania Blacka-Scholesa).
| (10.44) |
![]() ,
, ![]() z warunkiem końcowym
z warunkiem końcowym ![]() dla
dla ![]() oraz warunkiem brzegowym
oraz warunkiem brzegowym ![]() dla
dla ![]() (bo
wypłata zerowa nic nie kosztuje).
(bo
wypłata zerowa nic nie kosztuje).
Z parytetu wynika, że
(w przeciwnym przypadku istnieje arbitraż) oraz ![]() . Stąd
. Stąd
| (10.45) |
Dla ![]() lewa strona (10.45) jest
równa zeru, więc i prawa.
lewa strona (10.45) jest
równa zeru, więc i prawa.
Ćwiczenie 10.13
Znaleźć cenę forward dla kursu walutowego.
Rozważmy portfel składający się w chwili zero
z ![]() jednostek waluty zagranicznej,
jednostek waluty zagranicznej, ![]() jednostek
waluty krajowej i
jednostek
waluty krajowej i ![]() kontraktów forward
na otrzymanie jednej jednostki waluty zagranicznej z ceną forward
w chwili 0 równą
kontraktów forward
na otrzymanie jednej jednostki waluty zagranicznej z ceną forward
w chwili 0 równą ![]() . Nie zmieniamy tego portfela do chwili
. Nie zmieniamy tego portfela do chwili ![]() .
Wartość tego portfela w walucie krajowej w chwili 0 i
.
Wartość tego portfela w walucie krajowej w chwili 0 i ![]() wynosi:
wynosi:
Ponieważ na rynku nie ma możliwości arbitrażu, więc musi być
![]() , a stąd
, a stąd
Ćwiczenie 10.14
Udowodnić, że w chwili 0 cena opcji walutowej
o wypłacie ![]() jest identyczna w walucie krajowej i zagranicznej.
jest identyczna w walucie krajowej i zagranicznej.
(szkic). Jak wiemy, cena obcej waluty ![]() jest kursem wymiany i przy mierze martyngałowej
jest kursem wymiany i przy mierze martyngałowej ![]() jest
zadana równaniem
jest
zadana równaniem
![]() jest
jest ![]() -procesem Wienera i cena opcji w chwili 0 wynosi
-procesem Wienera i cena opcji w chwili 0 wynosi
![]() . Z punktu widzenia posiadacza waluty zagranicznej
kurs wymiany jest procesem
. Z punktu widzenia posiadacza waluty zagranicznej
kurs wymiany jest procesem ![]() , instrument bez ryzyka
spełnia równanie
, instrument bez ryzyka
spełnia równanie ![]() , a wypłata z opcji wynosi
, a wypłata z opcji wynosi
![]() . Naśladując postępowanie przeprowadzone dla akcji
z dywidendą, otrzymujemy, że miara martyngałowa
. Naśladując postępowanie przeprowadzone dla akcji
z dywidendą, otrzymujemy, że miara martyngałowa ![]() dla
procesu cen
dla
procesu cen ![]() spełnia
spełnia
gdzie ![]() jest
jest ![]() -procesem
Wienera. Cena wypłaty w walucie zagranicznej wynosi
-procesem
Wienera. Cena wypłaty w walucie zagranicznej wynosi
![]() i sprawdzamy, że
i sprawdzamy, że
korzystając z tego, że potrafimy znaleźć postać ![]() :
:
a) Proces ![]() jest procesem
jest procesem ![]() z ćw. 10.14.
z ćw. 10.14.
b) Nie wprost. Załóżmy, że jest to estymator nieobciążony. Wtedy dla
prawdopodobieństwa rzeczywistego ![]() otrzymalibyśmy
otrzymalibyśmy ![]() dla waluty krajowej i
dla waluty krajowej i ![]() dla waluty
zagranicznej. Zatem
dla waluty
zagranicznej. Zatem
| (10.46) |
sprzeczność z nierównością Jensena (funkcja ![]() jest
wypukła). Zatem estymator nieobciążony dla waluty krajowej nie może
być estymatorem nieobciążonym dla waluty zagranicznej i na odwrót.
Równość (10.46) zachodzi tylko w świecie deterministycznym,
czyli gdy
jest
wypukła). Zatem estymator nieobciążony dla waluty krajowej nie może
być estymatorem nieobciążonym dla waluty zagranicznej i na odwrót.
Równość (10.46) zachodzi tylko w świecie deterministycznym,
czyli gdy ![]() .
.




