Zagadnienia

12.1 Zagadnienia i zadania na ćwiczenia

12. Rynek Blacka-Scholesa kontraktów futures

Celem tego paragrafu będzie przedstawienie metody wyceny opcji na kontrakty futures. Gdy rozważamy instrument o cenie $S$ , to na rynku bez możliwości arbitrażu cena (kurs rozliczeniowy) $f_{S}(t,T)$ kontraktu futures z datą wykonania $T$ w chwili $t$ na instrument o cenie $S_{t}$ jest równa

$f_{S}(t,T)=e^{{r(T-t)}}S_{t}$

(12.1)

(co wynika z rozumowania arbitrażowego). Gdybyśmy zatem wyceniali opcje kupna na kontrakt futures z datą realizacji $T$ na akcje na rynku Blacka-Scholesa, to $f_{S}(T,T)=S_{T}$ i wypłata wynosi

$C_{T}^{f}:=(f_{S}(T,T)-K)^{+}=(S_{T}-K)^{+},$

(12.2)

czyli możemy skorzystać ze wzoru Blacka-Scholesa dla ceny opcji kupna. Problem zaczyna się gdy data realizacji opcji $T$ na kontrakt futures jest różna od daty zamknięcia tego kontraktu futures $U$ , gdyż wtedy wypłata nie spełnia warunku (12.2) (istotnie, $f_{S}(T,U)\neq S_{T}$ i $C_{T}^{f}=(f_{S}(T,U)-K)^{+}\not=(S_{T}-K)^{+}\ )$ i powyższe rozumowanie zawodzi. Jest to sytuacja typowa na rynku. Spróbujmy na to spojrzeć inaczej, tak by ominąć tę trudności. Ponieważ na rynku Blacka-Scholesa cena $S_{t}$ jest dana wzorem (9.2), więc z (12.1) dla kontraktu futures o terminie wykonania $U=T$ mamy

$\displaystyle f_{S}(t,U)=e^{{r(U-t)}}S_{0}e^{{(\mu-\frac{1}{2}\sigma^{2})t+\sigma W_{t}}}=f_{S}(0,U)e^{{(\mu-r-\frac{1}{2}\sigma^{2})t+\sigma W_{t}}}.$

Oznaczając $f_{t}=f_{S}(t,U)$ otrzymujemy stąd, że $f_{t}$ jest jedynym rozwiązaniem równania:

$\begin{cases}df_{t}=(\mu-r)f_{t}dt+\sigma f_{t}dW_{t},\quad t\in[0,U],\cr f_{0}=S_{0}e^{{rU}}.\end{cases}$

Ponieważ kontrakt futures nie musi być związany z konkretnym istniejącym aktywem, więc zapominamy o akcji i na kontrakt patrzymy jako na instrument finansowy, którego cena spełnia równanie:

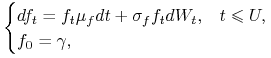$\begin{cases}df_{t}=f_{t}\mu _{f}dt+\sigma _{f}f_{t}dW_{t},&t\leq U,\\ f_{0}=\gamma,\end{cases}$

(12.3)

gdzie $\gamma$ , $\mu _{f}$ , $\sigma _{f}>0$ są stałymi. Instrument ten w dalszym ciągu jednak odzwierciedla sytuację, że w chwili $t$ umawiamy się, iż w przyszłości w chwili $T$ zapłacimy ustaloną cenę za ustalone w umowie dobro. Mając równanie opisujące ceny instrumentu finansowego, konstruujemy rynek kontraktów futures postępując analogicznie jak przy konstrukcji modelu rynku Blacka-Scholesa. Na rynku futures mamy dwa aktywa: bezryzykowne o cenie $B$ i kontraktu futures o cenie $f$ . Strategia to, jak zawsze, para procesów adaptowanych $\varphi=(\varphi^{0},\varphi^{1})$ , ale proces bogactwa jest zadany wzorem

$V_{t}^{f}(\varphi)=\varphi _{t}^{0}B_{t},\quad t\in[0,T],$

(12.4)

gdyż wejście w kontrakt futures nic nie kosztuje. Mówimy, że $\varphi$ jest strategią samofinansującą się, gdy

$V_{t}^{f}(\varphi)=V_{0}^{f}(\varphi)+\int _{0}^{t}\varphi^{0}_{u}dB_{u}+\int _{0}^{t}\varphi _{u}^{1}df_{u}.$

(12.5)

Definicja 12.1

Miarę probabilistyczną $\bar{P}$ nazywamy miarą martyngałową futures, gdy $\bar{P}\sim P$ i proces cen $f$ jest $\bar{P}$ -lokalnym martyngałem.

Twierdzenie 12.1

Dla procesu $f$ zadanego równaniem (12.3) miara martyngałowa futures $\bar{P}$ jest dana wzorem

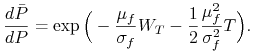$\frac{d\bar{P}}{dP}=\exp\Big(-\frac{\mu _{f}}{\sigma _{f}}W_{T}-\frac{1}{2}\frac{\mu _{f}^{2}}{\sigma _{f}^{2}}T\Big).$

(12.6)

Dynamika cen $f$ przy mierze $\bar{P}$ ma postać:

$df_{t}=\sigma _{f}f_{t}d{\overline{W}}_{t},$

(12.7)

gdzie ${\overline{W}}_{t}=W_{t}+\Big(\frac{\mu _{f}}{\sigma _{f}}\Big)t$ jest $\bar{P}$ -procesem Wienera.

Dowód tego twierdzenia pozostawiamy jako ćwiczenie. Warto zauważyć, że ${\cal F}_{t}={\cal F}_{t}^{W}={\cal F}_{t}^{f}$ .

Od tego momentu dla wygody będziemy pisać $\mu$ , $\sigma$ zamiast $\mu _{f},\sigma _{f}$ , czyli będziemy opuszczali wskaźnik dolny $f$ we wzorach związanych z $f_{t}$ . Z warunku (12.7) wynika, że

$f_{t}=f_{0}\ \exp\Big(\sigma{\overline{W}}_{t}-\frac{\sigma^{2}t}{2}\Big),$

(12.8)

a więc $f_{t}$ jest martyngałem dodatnim. Mówimy, że strategia $\varphi$ jest dopuszczalna, gdy jest strategią samofinansującą się i $B_{t}^{{-1}}V_{t}(\varphi)$ jest $\bar{P}$ -martyngałem. Zbiór takich strategii będziemy oznaczać przez $\Phi^{f}$ . Modelem Blacka rynku futures nazywamy trójkę ${\cal M}^{f}=(B,f,\Phi^{f})$ . Jest to rynek wolny od arbitrażu (ćw. 12.3).

Tak samo, jak dla rynku Blacka-Scholesa, wprowadzamy pojęcie ceny arbitrażowej. Wycenę opcji kupna przedstawia

Twierdzenie 12.2

(Black) Cena arbitrażowa $C^{f}$ opcji kupna na rynku futures ${\cal M}^{f}$ z terminem wykonania $T$ i ceną wykonania $K$ jest w chwili $t$ równa

$C_{t}^{f}=C^{f}(f_{t},T-t),$

(12.9)

gdzie

$\displaystyle C^{f}(x,t)$	$\displaystyle=$	$\displaystyle e^{{-rt}}(xN(\bar{d_{1}}(x,t))-KN(\bar{d_{2}}(x,t))),$
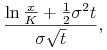$\displaystyle\bar{d}_{1}(x,t)$	$\displaystyle=$	$\displaystyle\frac{\ln\frac{x}{K}+\frac{1}{2}\sigma^{2}t}{\sigma\sqrt{t}},$
$\displaystyle\bar{d}_{2}(x,t)$	$\displaystyle=$	$\displaystyle\bar{d}_{1}(x,t)-\sigma\sqrt{t}.$

Ponieważ $C_{t}^{f}=B_{t}E_{{\bar{P}}}((f_{T}-K)^{+}B_{T}^{{-1}}|{\cal F}_{t})$ , więc dowód przebiega analogicznie do dowodu formuły Blacka-Scholesa, choć z oczywistymi zmianami.

∎

Wzór (12.9) jest nazywany wzorem Blacka. Dla cen opcji kupna i sprzedaży na kontrakty futures zachodzi związek, nazywany jak zawsze formułą zgodności (parytetem)

$C_{t}^{f}-P_{t}^{f}=e^{{-r(T-t)}}(f_{t}-K).$

(12.10)

Stąd otrzymujemy wzór na cenę opcji sprzedaży

$P_{t}^{f}=e^{{-r(T-t)}}(KN(-\bar{d_{2}}(f_{t},T-t))-f_{t}N(-\bar{d_{1}}(f_{t},T-t))).$

(12.11)

Przykład 12.1

Rozpatrzmy opcję sprzedaży na kontrakty futures na ropę naftową. Czas do wygaśnięcia to 4 miesiące. Obecna cena futures wynosi 30, cena wykonania 32, stopa procentowa bez ryzyka $5\%$ p.a., a współczynnik zmienności $20\%$ p.a. Cenę tej opcji obliczamy ze wzoru (12.11). Ponieważ $T-t=\frac{1}{3}$ , $f_{t}=30$ , $K=32$ , $r=0{,}05$ , $\sigma=0{,}2$ , więc $P_{t}^{f}=2{,}60$ ; $C_{t}^{f}=0{,}63$ .