Zagadnienia

5.1 Model CRR
5.2 Problemu maksymalizacji oczekiwanej użyteczności
5.3 Aproksymacje za pomocą modeli dwumianowych
5.4 Zagadnienia i zadania na ćwiczenia

5. Model dwumianowy (Coxa-Rossa-Rubinsteina)

Rozważymy teraz prosty, ale bardzo ważny model Coxa-Rossa-Rubinsteina (CRR). Nazywa go się także modelem dwumianowym. Powstał później niż model Blacka-Scholesa. Ma zastosowanie przy konstrukcji metod numerycznych dla obliczania cen różnych skomplikowanych wypłat.

5.1. Model CRR

Na rynku są dwa podstawowe instrumenty, rachunek bankowy z procesem cen:

$B_{{t}}=(1+r)^{{t}},\quad t=0,\dots,T$

i instrument ryzykowny (np. akcja) z procesem cen zadanym wzorem:

$S_{0}=s>0,\quad S_{{t+1}}=S_{{t}}U_{{t+1}},\quad t=0,1,\dots,T-1,$

(5.1)

gdzie $U_{{t}}$ są niezależnymi zmiennymi losowymi o jednakowym rozkładzie

$P(U_{{t}}=1+b)=p,\quad P(U_{{t}}=1+a)=1-p,\quad p\in(0,1),$

przy czym $-1<a<b$ . Wielkości $a$ i $b$ są stopami zwrotu z akcji, gdy cena zmienia się odpowiednio na $S_{{t}}(1+a)$ i $S_{{t}}(1+b)$ , gdyż

$\frac{S_{{t+1}}-S_{{t}}}{S_{{t}}}=U_{{t+1}}-1.$

Z tej definicji widać, że na model CRR można patrzeć jako na niezależne jednookresowe dwustanowe modele o tej samej stopie zwrotu, gdyż można ten model zrealizować na przestrzeni probabilistycznej $(\Omega,{\cal F},P)$ , gdzie $\Omega=\{ 1+a,1+b\}^{{T}}$ , ${\cal F}=2^{{\Omega}}$ , zaś $P$ jest prawdopodobieństwem produktowym jednoznacznie wyznaczonym przez $p$ . Wtedy

$U_{{t}}((\omega _{{1}},\dots,\omega _{{T}}))=\omega _{{t}}\quad\hbox{i}\quad{\cal F}_{t}=\sigma(S_{0},S_{{1}},\dots,S_{{t}})=\sigma(U_{{1}},\dots,U_{{t}}).$

Zbadamy własności tak zdefiniowanego modelu rynku. Rozpatrzymy model ogólniejszy. Niech $\Omega,{\cal F},U_{{t}},S_{{t}}$ będą określone jak wyżej, natomiast $P$ jest pewnym prawdopodobieństwem na ${\cal F}$ . Zauważmy, że

$P(\{(\omega _{{1}},\dots,\omega _{{T}})\})=P(U_{{1}}=\omega _{{1}},\dots,U_{{T}}=\omega _{{T}}),$

(5.2)

zatem znajomość prawdopodobieństwa $P$ jest równoważna znajomości rozkładu łącznego wektora $(U_{{1}},\dots,U_{{T}})$ .

Do badania własności użyjemy aparatu miar martyngałowych. Dlatego zaczynamy od nastepującego lematu:

Lemat 5.1

$(S_{{t}}^{{*}})_{{t\in{\cal T}}}$ jest martyngałem względem rozkładu prawdopodobieństwa $P^{*}$ wtedy i tylko wtedy, gdy

$\forall _{{t\leq T-1}}\quad E_{{P^{*}}}(U_{{t+1}}|{\cal F}_{{t}})=1+r.$

$E_{{P^{*}}}(S_{{t+1}}^{{*}}|{\cal F}_{{t}})=S_{{t}}^{{*}}\quad\Leftrightarrow\quad E_{{P^{*}}}(\frac{S_{{t+1}}^{{*}}}{S_{{t}}^{{*}}}|{\cal F}_{{t}})=1\quad\Leftrightarrow\quad E_{{P^{*}}}(\frac{U_{{t+1}}}{1+r}|{\cal F}_{{t}})=1.$

∎

Wniosek 5.1

Jeśli rynek jest wolny od arbitrażu, to $r\in(a,b)$ .

Gdy rynek jest wolny od arbitrażu, to istnieje miara martyngałowa $P^{*}$ dla $S_{{t}}^{{*}}$ , więc z lematu 5.1 mamy $E_{{P^{{*}}}}(U_{{t+1}}|{\cal F}_{{t}})=1+r$ , czyli $E_{{P^{{*}}}}(U_{{t+1}})={=}1+r$ . Ale $U_{{t+1}}$ przyjmuje z dodatnim prawdopodobieństwem wartości $1+a$ oraz $1+b$ , więc średnia należy do wnętrza przedziału, tj. $(1+r)\in(1+a,1+b)$ .

∎

Z lematu 5.1 otrzymujemy natychmiast istnienie miary martyngałowej, będącej miarą produktową, dla rynku CRR, gdy $r\in(a,b)$ .

Twierdzenie 5.1

Niech $r\in(a,b)$ . Jeśli $P$ jest produktowym rozkładem prawdopodobieństwa wyznaczonym przez $p=\frac{r-a}{b-a}$ , to zdyskontowany proces cen $S_{{t}}^{{*}}$ jest $P$ -martyngałem.

Z definicji prawdopodobieństwa $P$ i definicji $U_{t}$ wynika niezależność zmiennych $U_{1},\ldots,U_{T}$ . Stąd i z postaci rozkładu $U_{{t+1}}$ otrzymujemy

$E_{P}(U_{{t+1}}|{\cal F}_{{t}})=E_{P}U_{{t+1}}=p(1+b)+(1-p)(1+a)=1+r$

i lemat 5.1 kończy dowód.

∎

Jedyność miary martyngałowej wynika z kolejnego twierdzenia.

Twierdzenie 5.2

Jeśli rynek CRR jest wolny od arbitrażu, to jest zupełny.

Należy udowodnić, że jeśli zdyskontowany proces cen $S_{{t}}^{{*}}$ jest $P$ -martyngałem, to $P$ jest produktowym rozkładem prawdopodobieństwa wyznaczonym przez $p=\frac{r-a}{b-a}$ . Jest to równoważne faktowi, że $U_{{1}},\dots,U_{{T}}$ są niezależnymi zmiennymi losowymi o jednakowym rozkładzie:

$P(U_{{1}}=1+b)=\frac{r-a}{b-a}=1-P(U_{{1}}=1+a).$

Dla dowolnego $t$ z lematu 5.1 otrzymujemy $E_{P}(U_{{t+1}}|{\cal F}_{{t}})=1+r$ , a ponieważ zmienna losowa $U_{{t+1}}$ przyjmuje dwie wartości, więc

$(1+a)E_{P}({\bf 1}_{{\{ U_{{t+1}}=1+a\}}}|{\cal F}_{{t}})+(1+b)E_{P}({\bf 1}_{{\{ U_{{t+1}}=1+b\}}}|{\cal F}_{{t}})=1+r.$

(5.3)

Ponadto

$E_{P}({\bf 1}_{{\{ U_{{t+1}}=1+a\}}}|{\cal F}_{{t}})+E_{P}({\bf 1}_{{\{ U_{{t+1}}=1+b\}}}|{\cal F}_{{t}})=1.$

Stąd oznaczając

$Z_{t}=E_{P}({\bf 1}_{{\{ U_{{t+1}}=1+b\}}}|{\cal F}_{{t}})$

(5.4)

mamy z (5.3):

$(1+a)(1-Z_{t})+(1+b)Z_{t}=1+r.$

Rozwiązując to równanie otrzymujemy

$Z_{t}=\frac{r-a}{b-a},$

a więc $Z_{t}=Z$ jest zmienną losową stałą i jest taka sama dla każdego $t$ . Stąd dla dowolnego $t$

$P(U_{{t+1}}=1+b)=E_{P}Z=\frac{r-a}{b-a},$

(5.5)

czyli zmienne losowe $U_{{t}}$ mają jednakowy rozkład. Aby wykazać niezależność zmiennych losowych $U_{{t}}$ względem miary $P$ wystarczy udowodnić, że dla $t=T$ i dla dowolnych $x_{{i}}\in\{ 1+a,1+b\}$ zachodzi:

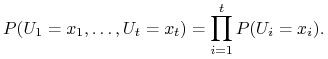$P(U_{{1}}=x_{{1}},\dots,U_{{t}}=x_{{t}})=\prod _{{i=1}}^{{t}}P(U_{{i}}=x_{{i}}).$

(5.6)

Dowodzimy (5.6) używając indukcji matematycznej (ćwiczenie 5.1).

Zatem rozkład $(U_{{1}},\dots,U_{{T}})$ jest produktowym rozkładem prawdopodobieństwa wyznaczonym przez $p=\frac{r-a}{b-a}$ ; teraz z (5.2) otrzymujemy, że prawdopodobieństwo martyngałowe $P$ jest produktowym rozkładem prawdopodobieństwa wyznaczonym przez $p=\frac{r-a}{b-a}$ .

∎

Ćwiczenie 5.1

Udowodnić (5.6).

Rozwiązanie:

Do dowodu (5.6) dla $t=T$ użyjemy indukcji matematycznej i wykażemy, że (5.6) zachodzi dla dowolnego $t\in{\cal T}$ , a więc i dla $t=T$ . Z (5.5) wynika, że (5.6) zachodzi dla $t=1$ . Zakładając, że równość (5.6) jest prawdziwa dla $t$ wykażemy, że jest również prawdziwa dla $t+1$ .

$\displaystyle P(U_{{1}}$	$\displaystyle=$	$\displaystyle x_{{1}},\dots,U_{{t+1}}=x_{{t+1}})=$
	$\displaystyle=$	$\displaystyle P(U_{{t+1}}=x_{{t+1}}\|U_{{1}}=x_{{t+1}},\dots,U_{{t}}=x_{{t}})P(U_{{1}}=x_{{1}},\dots,U_{{t}}=x_{{t}})=$
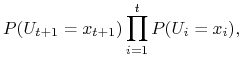	$\displaystyle=$	$\displaystyle P(U_{{t+1}}=x_{{t+1}})\prod _{{i=1}}^{{t}}P(U_{{i}}=x_{{i}}),$

gdzie w ostatniej równości skorzystaliśmy z (5.4), (5.5) i z założenia indukcyjnego.

Z dowodu twierdzenia mamy natychmiast.

Wniosek 5.2

Jeśli rynek CRR jest wolny od arbitrażu, to $U_{{1}},\dots,U_{{T}}$ są niezależnymi zmiennymi losowymi o jednakowym rozkładzie:

$P(U_{{1}}=1+b)=\frac{r-a}{b-a}=1-P(U_{{1}}=1+a).$

Założyliśmy, że stopa procentowa $r\geq 0$ , więc od tego momentu mówiąc o modelu CRR będziemy zawsze zakładać, że

$r\in(a,b)\quad\hbox{oraz}\quad r\geq 0.$

Twierdzenie 5.3

Cena arbitrażowa wypłaty $X$ w modelu CRR jest dana wzorem

$\Pi _{{t}}(X)=B_{{t}}E_{{P^{*}}}(XB_{{T}}^{{-1}}|{\cal F}_{{t}})\qquad{\rm dla}\ t\in{\cal T},$

gdzie miara martyngałowa $P^{{*}}$ jest wyznaczona przez $p=\frac{r-a}{b-a}$ .

Ponieważ model rynku CRR jest wolny od arbitrażu i zupełny, więc teza wynika natychmiast z tw. 4.3.

∎

Wniosek 5.3

Cena arbitrażowa europejskiej opcji kupna z terminem wykonania $T$ i ceną wykonania $K$ na akcję o cenie zadanej przez proces $S$ jest równa:

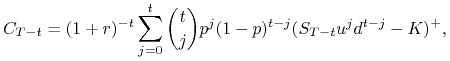$C_{{T-t}}=(1+r)^{{-t}}\sum _{{j=0}}^{{t}}{t\choose j}p^{{j}}(1-p)^{{t-j}}(S_{{T-t}}u^{{j}}d^{{t-j}}-K)^{{+}},$

(5.7)

gdzie $u=1+b$ , $d=1+a$ .

Ponieważ $S_{{u}}=s\prod _{{j=1}}^{{u}}U_{{j}}$ dla $u\in{\cal T}$ , więc

	$\displaystyle C_{{T-t}}$	$\displaystyle=$	$\displaystyle(1+r)^{{-t}}E_{{P^{{*}}}}((S_{{T}}-K)^{{+}}\|{\cal F}_{{T-t}})=$
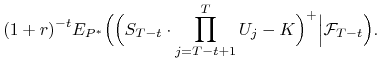		$\displaystyle=$	$\displaystyle(1+r)^{{-t}}E_{{P^{{*}}}}\Big(\Big(S_{{T-t}}\cdot\prod _{{j=T-t+1}}^{{T}}U_{{j}}-K\Big)^{{+}}\Big\|{\cal F}_{{T-t}}\Big).$

Korzystając z niezależności $\prod _{{j=T-t+1}}^{T}U_{{j}}$ od ${\cal F}_{{T-t}}$ i mierzalności $S_{{T-t}}$ względem ${\cal F}_{{T-t}}$ i znanego twierdzenia o obliczaniu takich wartości oczekiwanych mamy tezę.

∎

Cenę $C_{t}$ europejskiej opcji kupna z terminem wykonania $T$ i ceną wykonania $K$ w chwili $t$ otrzymujemy ze wzoru (5.7) i obserwacji $C_{t}=C_{{T-(T-t)}}$ .

Przykład 5.1

Niech w modelu CRR $S_{0}=100$ ; $S_{1}^{d}=80$ ; $S_{1}^{u}=130$ ; $T=2$ ; $r=0{,}1$ . Wycenić europejskie opcje kupna i sprzedaży z ceną wykonania 90.
Miara martyngałowa jest zadana przez $p=3/5$ . Z (5.7) lub wzoru ogólnego znajdujemy cenę opcji kupna $C_{0}=29{,}06$ , a z parytetu cenę opcji sprzedaży $P_{0}=3{,}44$ .

Problem replikacji. Zajmiemy się teraz problemem replikacji wypłaty postaci $X=h(S_{T})$ , dla pewnego $h\colon\mathbb{R}\to\mathbb{R}$ (taką postać wypłaty mają np. opcje). Gdy $\varphi$ replikuje $X$ , to

$X=V_{T}(\varphi)=V_{{T-1}}(\varphi)+\varphi^{1}_{T}(S_{T}-S_{{T-1}})+\varphi _{T}^{0}(B_{T}-B_{{T-1}}),$

zatem

$h(S_{{T-1}}U_{T})=V_{{T-1}}(\varphi)+\varphi _{T}^{1}S_{{T-1}}(U_{T}-1)+\varphi _{T}^{0}rB_{{T-1}}.$

Ponieważ $U_{T}$ przyjmuje dwie wartości: $(1+a)$ i $(1+b)$ , więc na zbiorze $U_{T}=1+a$ , mamy

$h(S_{{T-1}}(1+a))=V_{{T-1}}(\varphi)+\varphi _{T}^{1}S_{{T-1}}a+\varphi _{T}^{0}rB_{{T-1}},$

a na zbiorze $U_{T}=1+b$ , to mamy

$h(S_{{T-1}}(1+b))=V_{{T-1}}(\varphi)+\varphi _{T}^{1}S_{{T-1}}b+\varphi _{T}^{0}rB_{{T-1}}.$

Ponieważ proces $\varphi _{t}^{1}$ jest prognozowalny, więc $\varphi _{T}^{1}$ nie zależy od wartości $U_{T}$ . Zatem z powyższych równości otrzymujemy liczbę akcji w chwili $T$ :

$\varphi^{1}_{T}=\frac{h(S_{{T-1}}(1+b))-h(S_{{T-1}}(1+a))}{S_{{T-1}}(b-a)}=\Delta(S_{{T-1}}),$

gdzie

$\Delta(x)=\frac{h(x(1+b))-h(x(1+a))}{x(b-a)}$

oraz liczbę jednostek bankowych w chwili $T$

$\varphi _{T}^{0}=\frac{1}{rB_{{T-1}}}\Big[h(S_{{T-1}}(1+b))-V_{{T-1}}(\varphi)-b\frac{h(S_{{T-1}}(1+b))-h(S_{{T-1}}(1+a))}{b-a}\Big].$

W ten sposób, cofając się, znajdujemy postać portfela replikującego.

Ćwiczenie 5.2

Udowodnić, że portfel replikujący w chwili $t$ ma postać

	$\displaystyle\varphi _{t}^{1}$	$\displaystyle=$	$\displaystyle\frac{f(t,S_{{t-1}}(1+b))-f(t,S_{{t-1}}(1+a))}{S_{{t-1}}(b-a)},$		(5.8)
	$\displaystyle\varphi _{t}^{0}$	$\displaystyle=$	$\displaystyle\frac{(1+b)f(t,S_{{t-1}}(1+a))-(1+a)f(t,S_{{t-1}}(1+b))}{(b-a)(1+r)^{t}}.$		(5.9)

Rozwiązanie:

Ogólnie, w chwili $t$ musi zachodzić

$(1+r)^{{t-T}}E(h(S_{T})|{\cal F}_{t})=V_{t}(\varphi)=\varphi _{t}^{0}(1+r)^{t}+\varphi _{t}^{1}S_{t}.$

(5.10)

Jak wiemy, $S_{T}=S_{t}Z_{t},$ gdzie $Z_{t}=\Pi _{{j=t+1}}^{T}U_{j}$ , a więc

	$\displaystyle V_{t}(\varphi)$	$\displaystyle=$	$\displaystyle(1+r)^{{t-T}}E(h(S_{T})\|{\cal F}_{t})=(1+r)^{{t-T}}E(h(xZ_{t}))\Big\|_{{x=S_{t}}}=$		(5.11)
		$\displaystyle=$	$\displaystyle f(t,S_{t}).$		(5.11)

Z tego wynika, że wartość w chwili $t$ portfela replikującego wypłatę $h(S_{T})$ zależy tylko od obecnej wartości ceny, czyli od $S_{t}$ . Z (5.10) i (5.11) otrzymujemy

$\varphi _{t}^{1}S_{{t-1}}U_{t}=f(t,S_{{t-1}}U_{t})-(1+r)^{t}\varphi _{t}^{0},$

czyli

$\varphi _{t}^{1}S_{{t-1}}(1+a)=f(t,S_{{t-1}}(1+a))-(1+r)^{t}\varphi^{0}_{t}$

$\varphi _{t}^{1}S_{{t-1}}(1+b)=f(t,S_{{t-1}}(1+b))-(1+r)^{t}\varphi^{0}_{t}.$

Zatem zachodzi (5.8) i proces $\varphi _{t}^{1}$ jest prognozowalny. Ponadto

	$\displaystyle\varphi _{t}^{0}$	$\displaystyle=$	$\displaystyle\frac{f(t,S_{{t-1}}(1+b))+f(t,S_{{t-1}}(1+a))-\varphi _{t}^{1}S_{{t-1}}(2+a+b)}{2(1+r)^{t}}$
		$\displaystyle=$	$\displaystyle\frac{(1+b)f(t,S_{{t-1}}(1+a))-(1+a)f(t,S_{{t-1}}(1+b))}{(b-a)(1+r)^{t}}.$

Na wzór (5.8) można spojrzeć jako na dyskretny analog pochodnej wartości portfela względem możliwej zmiany ceny instrumentu podstawowego. W języku finansów takie strategie nazywa się delta zabezpieczeniem.

Z (5.8) otrzymujemy też

Wniosek 5.4

Gdy $h$ jest funkcją rosnącą, to $\varphi _{t}^{1}\geq 0$ . Zatem można replikować wypłatę $h(S_{T})$ bez korzystania z krótkiej sprzedaży.

W szczególności wynika stąd, że można tak replikować wypłatę z europejskiej opcji kupna.

5.2. Problemu maksymalizacji oczekiwanej użyteczności

Rozważymy teraz na przykładzie modelu CRR problem maksymalizacji oczekiwanej użyteczności. Inwestor ma swoją miarę użyteczności osiągniętego bogactwa, jest to funkcja użyteczności $U\colon(0,\infty)\to\mathbb{R}$ . Wartość $U(x)$ opisuje satysfakcję inwestora posiadającego kapitał $x$ . Wartość inwestycji mierzy się przez oczekiwaną użyteczność (przy mierze subiektywnej $P$ ) kapitału osiągniętego na końcu inwestycji, czyli przez $E_{P}U(V_{T}(\varphi))$ .

Funkcję $U\colon(0,\infty)\to\mathbb{R}$ nazywamy funkcją użyteczności, gdy jest niemalejąca, wklęsła, różniczkowalna i ma ciągłą pochodną. Często o $U$ zakłada się, że spełnia tzw. warunki Inady:

$\lim _{{x\to 0}}U^{{\prime}}(x)=\infty,\qquad\lim _{{x\to\infty}}U^{{\prime}}(x)=0.$

Najczęściej używane są: logarytmiczna funkcja użyteczności $U(x)=\ln x$ , potęgowa $U(x)=\frac{x^{\alpha}}{\alpha}$ , $\alpha\in(-\infty,0)\cup(0,1)$ oraz wykładnicza funkcja użyteczności $U(x)=1-\exp(-bx)$ , $b>0$ .

Naszym celem jest znalezienie, przy danym kapitale początkowym $x$ , strategii samofinansującej się $\varphi^{*}$ maksymalizującej oczekiwaną użyteczność kapitału osiągniętego na końcu inwestycji, czyli strategii $\varphi^{*}$ takiej że $V_{0}(\varphi^{*})=x$ i

$E_{P}\ \Big(U(V_{T}(\varphi^{*}))\ \Big)=\max _{{\varphi\in\Phi,\ V_{0}(\varphi)=x}}E_{P}\ \Big(U(V_{T}(\varphi))\ \Big).$

(5.12)

Rozwiążemy ten problem w przypadku funkcji logarytmicznej $U(x)=\ln x$ , rozszerzając ją na $(-\infty,0]$ wzorem $U(x)=-\infty$ . Ponieważ

$\ln V_{T}(\varphi)=\ln V^{*}_{T}(\varphi)+\ln B_{T},$

więc problem optymalizacji sprowadza się do znalezienia maksimum

$\max _{{\varphi\in\Phi,\ V_{0}(\varphi)=x}}E_{P}(\ln V_{T}^{*}(\varphi)).$

Skorzystamy z faktu, że $V_{T}^{*}(\varphi)$ jest $P^{*}$ -martyngałem, gdy $P^{*}$ jest miarą martyngałową, z czego wynika, że $E_{{P^{*}}}V_{T}^{*}(\varphi)=V_{0}(\varphi)$ . Niech

	$\displaystyle dP^{*}$	$\displaystyle=$	$\displaystyle Z_{T}dP,$
	$\displaystyle Y_{t}$	$\displaystyle=$	$\displaystyle E_{{P^{*}}}(xZ_{T}^{{-1}}\|{\cal F}_{t}).$

Wtedy $Y_{t}$ jest $P^{*}$ -martyngałem i $Y_{T}=xZ_{T}^{{-1}}$ oraz $Y_{0}=x$ . Udowodnimy, że

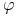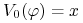
a) Dla dowolnej strategii samofinansującej się $\varphi$ , takiej że $V_{0}(\varphi)=x$

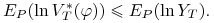
$E_{P}(\ln V_{T}^{*}(\varphi))\leq E_{P}(\ln Y_{T}).$ (5.13)
b) Istnieje strategia samofinansująca się 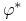$\varphi^{*}$ , taka że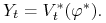

$Y_{t}=V^{*}_{t}(\varphi^{*}).$ (5.14)

Dla każdego $\varphi\in\Phi$ takiego, że $V_{0}(\varphi)=x$ zachodzi

$\displaystyle E_{P}(\ln V_{T}^{*}(\varphi))$	$\displaystyle=$	$\displaystyle E_{P}\Big(\ln\frac{x}{Z_{T}}+\ln V_{T}^{*}(\varphi)-\ln\frac{x}{Z_{T}}\Big)\leq$
	$\displaystyle\leq$	$\displaystyle E_{P}\Big(\ln\frac{x}{Z_{T}}\Big)+E_{P}\Big(\frac{Z_{T}}{x}V_{T}^{*}(\varphi)-1\Big)=$
	$\displaystyle=$	$\displaystyle E_{P}\Big(\ln\frac{x}{Z_{T}}\Big)+\frac{1}{x}E_{{P^{}}}\Big(V_{T}^{}(\varphi))-1=E_{P}(\ln Y_{T}),$

co daje (5.13).
Z zupełności rynku istnieje strategia samofinansująca się $\varphi^{*}$ spełniająca $V_{T}^{*}(\varphi)=Y_{T}$ , a ponieważ $Y$ jest $P^{*}$ -martyngałem, to (5.14) zachodzi.
Okazuje się, że jak na rynku skończonym potrafimy znaleźć $\varphi^{*}$ spełniające (5.12), to na rynku skończonym nie ma arbitrażu.

Ćwiczenie 5.3

Niech $U$ będzie funkcją ściśle monotoniczną. Jeśli istnieje rozwiązanie zagadnienia (5.12), to na rynku nie ma arbitrażu.

Wskazówka:

Przeprowadzić rozumowanie niewprost.

5.3. Aproksymacje za pomocą modeli dwumianowych

Gdy obserwujemy rynek z czasem ciągłym, czyli gdy czas jest odcinkiem $[0,T]$ , to ceny należy opisywać modelem, w którym występują procesy z czasem ciągłym. Ale jak wiadomo, przy opisie rozmaitych zjawisk można modele z czasem ciągłym z powodzeniem aproksymować modelami dyskretnymi. Teraz opiszemy, jak wykorzystuje się model CRR do aproksymacji modelu z czasem ciągłym.

Konstruuje się ciąg przybliżeń, w którym jako $n$ -te przybliżenie bierze się model CRR skonstruowany następująco:

W tym (czyli $n$ -tym) kroku dzielimy odcinek $[0,T]$ na $n$ części o długości $\delta _{{n}}={=}\frac{T}{n}$ każda. Zakładamy, że handel odbywa się w chwilach czasu $t_{{j}}=t_{{j}}^{{(n)}}=j\delta _{{n}}$ , $j=0,1,\dots,n$ . W czasie ciągłym rachunek oszczędnościowy jest opisywany przez równanie $B_{{t}}=e^{{rt}}$ ( $r>0$ jest stałą). Chcemy dopasować stopę procentową $r_{{n}}$ tak, żeby otrzymać równość cen rachunków oszczędnościowych w modelu ciągłym i dyskretnym we wszystkich punktach $t_{{j}}$ . W tym celu bierzemy $r_{{n}}$ takie, że

$1+r_{{n}}=e^{{r\delta _{{n}}}}.$

Wtedy

$B_{{t_{{j}}}}=e^{{rj\delta _{{n}}}}=(e^{{r\delta _{{n}}}})^{{j}}=(1+r_{{n}})^{{j}}.$

Teraz dobieramy stałe $a_{{n}}$ i $b_{{n}}$ spełniające

$-1<a_{{n}}<r_{{n}}<b_{{n}}$

(5.15)

(wtedy model CRR jest bez możliwości arbitrażu i zupełny). Warunek (5.15) musi być spełniony, poza tym wyboru $a_{{n}}$ i $b_{{n}}$ dokonujemy tak, by model graniczny opisywał model z czasem ciągłym. Zrobimy to w taki sposób, by

$u_{n}d_{n}=(1+b_{{n}})(1+a_{{n}})=1.$

Taki wybór zakłada pewien rodzaj symetrii ruchu cen. Niech

$1+a_{{n}}=e^{{-\sigma\sqrt{\delta _{{n}}}}},\qquad 1+b_{{n}}=e^{{\sigma\sqrt{\delta _{{n}}}}},$

gdzie $\sigma>0$ jest ustalona z góry. Łatwo sprawdzić, że nierówność (5.15) zachodzi dla dostatecznie dużych $n$ . Wtedy miara martyngałowa jest zadana przez podanie prawdopodobieństwa wzrostu ceny akcji

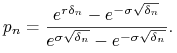$p_{{n}}=\frac{e^{{r\delta _{{n}}}}-e^{{-\sigma\sqrt{\delta _{{n}}}}}}{e^{{\sigma\sqrt{\delta _{{n}}}}}-e^{{-\sigma\sqrt{\delta _{{n}}}}}}.$

Zachodzi

Ćwiczenie 5.4

Udowodnić, że $p_{{n}}\to 1/2$ , gdy $n\to\infty$ .

W ten sposób skonstruowaliśmy $n$ -ty model CRR dla ciągu przybliżeń. Parametry $a_{n},b_{n},p_{n}$ są ustalone i zależą od parametrów $r,\sigma$ i liczby kroków $n$ , a więc długości podziału $\delta _{n}$ . Pozostaje pytanie, jak dobrać parametry $n$ -tego przybliżenia. Stopę procentową bez ryzyka $r$ znamy. Parametr $\sigma$ wybieramy tak, by wariancja stopy zwrotu z akcji na jednostkę czasu była równa wariancji na jednostkę czasu z modelu ciągłego (modelu Blacka-Scholesa opisanego w §9.1). Liczbę $n$ dobieramy według naszych potrzeb (ten parametr możemy zmieniać), byle $n$ było dostatecznie duże (zad. 5.11).

Możemy też bez straty ogólności założyć, że wszystkie modele (a więc i procesy z nimi związane) są skonstruowane na wspólnej przestrzeni probabilistycznej $(\Omega,{\cal F},P)$ . Zakładamy też, że cena początkowa aktywa w każdym przybliżeniu jest taka sama. Jak wiemy, cena $S^{{(n)}}$ aktywa ryzykownego w $n$ -tym modelu spełnia

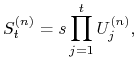$S_{{t}}^{{(n)}}=s\prod _{{j=1}}^{{t}}U^{{(n)}}_{{j}},$

gdzie $P(U^{{(n)}}_{{j}}=1+b_{{n}})=p_{{n}}$ , $P(U^{{(n)}}_{{j}}=1+a_{{n}})=1-p_{{n}}$ , $S_{0}^{{(n)}}=s$ i zmienne losowe $U^{{(n)}}_{1}$ , …, $U^{{(n)}}_{n}$ są niezależne, o tym samym rozkładzie. Zapiszmy to dla $t=T$ inaczej:

$S_{{T}}^{{(n)}}=se^{{\sigma\sqrt{\delta _{n}}\sum _{{j=1}}^{{n}}V^{{(n)}}_{{j}}}},$

gdzie $V^{{(n)}}_{{j}}=\frac{\ln U^{{(n)}}_{j}}{\sigma\sqrt{\delta _{n}}}$ , zatem $V^{{(n)}}_{{j}}$ są niezależnymi zmiennymi losowymi o jednakowym rozkładzie

$P(V^{{(n)}}_{{j}}=1)=p_{{n}}=1-P(V^{{(n)}}_{{j}}=-1).$

Z centralnego twierdzenia granicznego otrzymujemy po przekształceniach

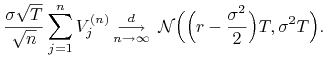$\frac{\sigma\sqrt{T}}{\sqrt{n}}\sum _{{j=1}}^{{n}}V_{{j}}^{{(n)}}\mathop{\longrightarrow}\limits _{{n\to\infty}}^{d}\ {\cal N}\Big(\Big(r-\frac{\sigma^{{2}}}{2}\Big)T,\sigma^{{2}}T\Big).$

(5.16)

Stąd, gdy $n\to\infty$ , to

$\ln S_{{T}}^{{(n)}}\mathop{\longrightarrow}\limits _{{n\to\infty}}^{d}\ \ln s+(r-\frac{\sigma^{{2}}}{2})T+\sigma\sqrt{T}Z,$

(5.17)

gdzie $Z\sim{\cal N}(0,1)$ , czyli

$S_{{T}}=S_{0}\exp\Big((r-\frac{\sigma^{{2}}}{2})T+\sigma\sqrt{T}Z\Big).$

Zatem cena w chwili $T$ otrzymana w granicy ma rozkład lognormalny (ten sam rezultat otrzymujemy dla dowolnego $t$ ).

Każdy z modeli CRR użyty w tej aproksymacji był bez możliwości arbitrażu i zupełny, więc wiemy, że cena arbitrażowa europejskiej opcji kupna $C_{{T}}^{{(n)}}$ jest zadana wzorem (5.7) z $p=p_{{n}}$ . W granicy otrzymujemy

Twierdzenie 5.4

$\lim _{{n\to\infty}}C_{{T}}^{{(n)}}=sN(d_{{1}}(s,T))-Ke^{{-rT}}N(d_{2}(s,T)),$

(5.18)

gdzie $N$ oznacza dystrybuantę standardowego rozkładu gaussowskiego oraz

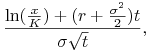	$\displaystyle d_{{1}}(x,t)$	$\displaystyle=$	$\displaystyle\frac{\ln(\frac{x}{K})+(r+\frac{\sigma^{{2}}}{2})t}{\sigma\sqrt{t}},$		(5.19)
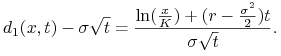	$\displaystyle d_{{2}}(x,t)$	$\displaystyle=$	$\displaystyle d_{{1}}(x,t)-\sigma\sqrt{t}=\frac{\ln(\frac{x}{K})+(r-\frac{\sigma^{{2}}}{2})t}{\sigma\sqrt{t}}.$		(5.20)

Dowód tego faktu pozostawiamy jako zadanie.

Podsumowując, powyższe rozważania o aproksymacji sugerują, że w ,,rozsądnym” modelu rynku cena aktywa powinna mieć rozkład lognormalny, a cena arbitrażowa europejskiej opcji kupna powinna być zadana wzorem BlackaS̄cholesa (5.18). Wzór (5.17) dowodzi że $S^{{(n)}}_{T}$ zbiega do $S_{T}$ według rozkładu, a więc gdy wypłata jest funkcją wartości końcowej ceny, tj. $X_{n}=f(S^{{(n)}}_{T})$ , to przy odpowiednich założeniach o funkcji $f$ otrzymujemy

$\Pi _{0}(f(S_{T}))=\lim _{{n\to\infty}}\Pi _{0}(f(S^{{(n)}}_{T})).$

(5.21)

Gdy $f$ jest ograniczona, to (5.21) zachodzi i w szczególności otrzymujemy formułę wyceny dla opcji sprzedaży (a stąd korzystając z parytetu można w inny sposób otrzymać (5.18)).

Okazuje się, że można udowodnić znacznie więcej o zbieżności aproksymacji. Rozpatrzmy proces $\hat{S}_{{t}}^{{(n)}}$ z czasem ciągłym otrzymany z procesu $S_{{t}}^{{(n)}}$ przez interpolację liniową, tj. $\hat{S}_{{t_{j}}}^{{(n)}}=S_{{t_{j}}}^{{(n)}}$ dla $t_{j}=\frac{jT}{n}$ i $\hat{S}_{{t}}^{{(n)}}$ jest liniowy pomiędzy punktami postaci $t_{j}$ . Korzystając z tw. Donskera można udowodnić, że proces $\hat{S}^{{(n)}}$ zbiega słabo w $C[0,T]$ do procesu $S$ , takiego że

$S_{{t}}=S_{0}\exp\Big((r-\frac{\sigma^{{2}}}{2})t+\sigma W_{t}\Big),$

gdzie $W_{t}$ jest procesem Wienera. Stąd otrzymujemy, że ceny pewnych wypłat, które zależą od całej trajektorii procesu cen można otrzymać jako granicę odpowiednich wyrażeń obliczanych dla modelu CRR. Ten fakt wykorzystujemy w modelu z czasem ciągłym do liczenia cen wypłat dla których nie istnieją jawne wzory. Model CRR jest modelem opisującym rynek w sposób rekurencyjny, więc w tym modelu znacznie łatwiej liczyć całki numerycznie niż w modelu z czasem ciągłym.

5.4. Zagadnienia i zadania na ćwiczenia

Ćwiczenie 5.5

Znaleźć cenę arbitrażową europejskiej opcji sprzedaży w modelu CRR.

Rozwiązanie:

Powtórzyć rozumowanie prowadzące do wzoru (5.7) lub skorzystać z parytetu kupno-sprzedaż.

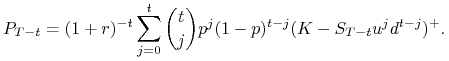$P_{{T-t}}=(1+r)^{{-t}}\sum _{{j=0}}^{{t}}{t\choose j}p^{{j}}(1-p)^{{t-j}}(K-S_{{T-t}}u^{{j}}d^{{t-j}})^{{+}}.$

Ćwiczenie 5.6

Niech w modelu CRR $S_{0}=100;S_{1}^{u}=120;S_{1}^{d}=90;T=3;r=0{,}05$ . Wycenić opcję europejską o wypłacie $X=100(R_{T}-0{,}10)^{+}$ , gdzie $R_{T}=\frac{S_{T}-S_{0}}{S_{0}}$ jest stopą zwrotu z akcji w czasie od 0 do $T$ .

Ćwiczenie 5.7

Rozpatrzmy model CRR, dla którego $S_{0}=100$ ; $u=1+b=1{,}2;d=1+a=0{,}7;T=2$ .

a) Dla jakich wartości stopy procentowej $r$ model jest wolny od arbitrażu? Wyznaczyć dla tych wartości miarę martyngałową.

b) Niech $r=10\%$ . Znaleźć cenę arbitrażową europejskich wypłat:

	$\displaystyle X$	$\displaystyle=$	$\displaystyle(\min(S_{1},S_{2})-90)^{+},$
	$\displaystyle Y$	$\displaystyle=$	$\displaystyle(S_{2}-S_{1}-10)^{+}.$

Rozwiązanie:

a) $r\in(0;0{,}2)$ . Miara martyngałowa $P^{*}$ jest zadana przez $p=2r+0{,}6$ .

b) $p=0{,}8$ ; $\Pi _{0}(X)=15{,}87$ ; $\Pi _{0}(Y)=7{,}93$ .

Ćwiczenie 5.8

Niech w modelu CRR $S_{0}=80;u=1,3;T=2;r=0{,}2$ .

a) Dla jakich $d$ model jest wolny od arbitrażu?

b) Dla $d=1{,}1$ wycenić opcję europejską o wypłacie $X=(\frac{S_{0}+S_{1}+S_{2}}{3}-85)^{+}$ . Znaleźć strategię replikującą.

Rozwiązanie:

a) $0<d<1{,}2$ ; b) Miara martyngałowa $P^{*}$ jest zadana przez $p=0{,}5$ , $\Pi _{0}(X)=8{,}38$ .

Ćwiczenie 5.9

Udowodnić, że w modelu CRR cena wypłaty postaci $X=g(S_{T})$ , gdzie $g\in C^{2}$ , $g(0)=0$ jest równa

$\Pi _{0}(X)=S_{0}g^{{\prime}}(0)+\int _{0}^{\infty}C_{0}(y)g^{{\prime\prime}}(y)dy,$

(5.22)

gdzie $C_{0}(y)$ jest ceną arbitrażową w chwili 0 europejskiej opcji kupna akcji o cenie $S$ z terminem wykonania $T$ i z ceną wykonania $y$ .

Rozwiązanie:

Wzór Taylora z resztą w postaci całkowej ma postać

$g(x)=g(0)+g^{{\prime}}(0)x+\int _{0}^{\infty}(x-y)^{+}g^{{\prime\prime}}(y)dy,$

a stąd wynika wzór (5.22).

Ćwiczenie 5.10

a) Znaleźć wariancję stopy zwrotu w $n$ -tym modelu CRR.

b) Znaleźć $\sigma$ znając wariancję stopy zwrotu (tj. przyjmując $D^{2}(U_{t})=A$ , gdzie $A$ jest wariancją teoretyczną z modelu ciągłego Blacka-Scholesa lub $A$ jest wariancją wyestymowaną z rynku.

c) Znaleźć $\sigma$ , gdy wybierzemy inny (ogólniejszy) $n$ -ty model CRR, czyli taki, że $u_{n}d_{n}=\gamma$ , gdzie $\gamma$ jest stałą dodatnią (dla $\gamma=1$ rozwiązanie otrzymaliśmy w punkcie b)).