Zagadnienia

11.1 Własności funkcji zysku i uogólnionego odwzorowania podaży
11.2 Minimalizacja kosztów

11. Teoria wyboru producenta – ciąg dalszy

11.1. Własności funkcji zysku i uogólnionego odwzorowania podaży

Teraz zajmiemy się ogólnymi własnościami zdefiniowanych obiektów.

Stwierdzenie 11.1 (Własności funkcji zysku)

a) w przypadku szczególnym $\Pi$ jest niemalejącą funkcją $p$ , ściśle rosnącą funkcją $p$ tam gdzie skończona i nierosnącą funkcją $\mathbf{w}$ ;

b) funkcja $\Pi$ jest jednorodna stopnia $1$ ;

c) funkcja $\Pi$ jest wypukła;

d) $\Pi$ jest ciągła na dowolnym zbiorze otwartym, na którym jest skończona;

e) Jeśli $\mathbb{Y}$ wypukły i ”no free lunch” (założenie 4), to istnieje $\mathbf{p}$ , dla którego $\Pi(\mathbf{p})$ skończone;

f) jeśli $\mathbb{Y}$ jest wypukły, to $\mathbb{Y}=\{\mathbf{y}\in\mathbb{R}^{{n}}:\mathbf{p}^{{T}}\mathbf{y}\leq\Pi(\mathbf{p})\ \forall\mathbf{p}\in\mathbb{R}_{{+}}^{{n}}\}$ – dualne wyrażenie zbioru $\mathbb{Y}$ .

Dowody a)-d) są podobne jak w stwierdzeniu 6.3.

e) Ponieważ ”nie ma czegoś takiego, jak obiadek za darmo”, jeśli weźmiemy dowolny punkt $a$ o wszystkich wspólrzędnych dodatnich np. $a=(1,\ldots,1)^{{T}}$ , to nie należy on do $\mathbb{Y}$ . Z twierdzenia o hiperpłaszczyźnie rozdzielającej będzie więc istniał wektor $\mathbf{p}\in\mathbb{R}^{{n}}$ , dla którego $\mathbf{p}^{{T}}a>\sup _{{y\in\mathbb{Y}}}\mathbf{p}^{{T}}\mathbf{y}$ . Pozostaje pokazać, że istnieje taki $\mathbf{p}$ , który może być wektorem cen, czyli, że ma wszystkie współrzędne dodatnie. Niech $p_{{i}}$ dla naszego $\mathbf{p}$ będzie ujemne. Niech $\mathbf{y}\in\mathbb{Y}$ . Z możliwości marnotrawstwa wynika, że jeśli $y_{{i}}$ zamienimy na dowolnie małą liczbę, to tak zmodyfikowany punkt będzie należał do $\mathbb{Y}$ , a więc nierówność $\mathbf{p}^{{T}}a>\sup _{{y\in\mathbb{Y}}}\mathbf{p}^{{T}}\mathbf{y}$ nie może być spełniona. Stąd wszystkie $p_{{i}}$ są nieujemne.

Co jeśli $p_{{i}}=0$ ? Weźmy dowolnie mały $\varepsilon>0$ i niech $\mathbf{p}^{{i,\varepsilon}}$ będzie równe $\mathbf{p}$ z $i$ -tą współrzędną zamienioną na $\varepsilon$ . Załóżmy, że żaden wektor $\mathbf{p}^{{i,\varepsilon}}$ nie jest hiperpłaszczyzną rozdzielającą. Niech $\mathbf{y}^{{\varepsilon}}$ oznacza punkt przecięcia hiperpłaszczyzny $\left(\mathbf{p}^{{i,\varepsilon}}\right)^{{T}}a=\left(\mathbf{p}^{{i,\varepsilon}}\right)^{{T}}\mathbf{y}$ z brzegiem $\mathbb{Y}$ . Wówczas z wypukłości $\mathbb{Y}$ i z tego, że $\mathbf{0}\in\mathbb{Y}$ , możemy otrzymać pewien ciąg $\mathbf{\bar{y}}^{{\varepsilon}}$ należących do przecięcia prostych łączących punkty $\mathbf{y}^{{\varepsilon}}$ , odpowiednio, z zerem i kuli domkniętej o promieniu $C\varepsilon$ (gdzie $C$ zależy od wartości pozostałych $p_{{i}}$ ) o środku w punkcie o $i$ -tej współrzędnej $1$ i wszytkich pozostałych współrzędnych $0$ . A to oznacza, że albo $\exists\mathbf{y}\in\mathbb{Y\cap R}_{{+}}^{{n}}$ , $\mathbf{y}\neq\mathbf{0}$ , albo $\mathbb{Y}$ nie jest domknięty.

f) Także z twierdzenia o hiperpłaszczyźnie rozdzielającej.

∎

Stwierdzenie 11.2 (Własności ogólnego odwzorowania podaży)

a) jeśli $\mathbb{Y}$ wypukły, to $\mathbf{y}$ ma wypukłe wartości, a jeśli $\mathbb{Y}$ jest ściśle wypukły, to $\mathbf{y}$ jest co najwyżej jednowartościowe;

b) Jeśli $\mathbf{y}\in\mathbf{y(p)}$ dla pewnego $\mathbf{p}$ , to $\mathbf{y\in}\mathop{\rm{Bd}}\mathbb{Y}$ i $\mathbf{y}$ jest efektywny.

c) Odwzorowanie $\mathbf{y}$ jest jednorodne stopnia $0$ ;

d) Odwzorowanie $\mathbf{y}$ jest górnie półciągłe na dowolnym zbiorze otwartym, na którym $\Pi$ skończone;

e) Jeśli $\mathbf{y}$ jest funkcją różniczkowalną w $\mathbf{p}$ , to $D\mathbf{y(p)\cdot p=0}$ .

Dowody a)-d) są podobne jak w stwierdzeniu 6.2; e) wynika z jednorodności stopnia $0$ .

∎

Stwierdzenie 11.3

(Lemat Hotellinga) jeśli $\mathbf{y}$ jest jednowartościowe i różniczkowalne, osiągane dla jednoznacznie wyznaczonych $\lambda$ i funkcja transformacji $F$ jest różniczkowalna, to $\Pi$ jest różniczkowalna i $\nabla\Pi=\mathbf{y}$ ;

Z twierdzenia o obwiedni.

∎

Ćwiczenie 11.1

Czy funkcja $\Pi(\mathbf{p})=p_{3}-\sqrt{p_{1}\cdot p_{2}}$ może być funkcją zysku firmy wolnokonkurencyjnej maksymalizującej zysk (sprawdzić wszystkie własności). Obliczyć (zakładając, że się da) uogólnione odwzorowanie podaży. Czy w tej technologii można wskazać jeden produkt? Czy można coś powiedzieć o przychodach skali?

Wniosek 11.1

Jeśli $\mathbf{y}$ jest funkcją różniczkowalną w $\mathbf{\bar{p}}$ to $D\mathbf{y}(\mathbf{\bar{p}})=D^{{2}}\Pi(\mathbf{\bar{p}})$ jest symetryczna i nieujemnie określona.

Z lematu Hotellinga i wypukłości $\Pi$ .

∎

Nieujemna określoność macierzy $D^{{2}}\Pi(\mathbf{\bar{p}})$ ma znów prostą interepretację ekonomiczną – jest to tzw. prawo podaży: podaż i ceny zmieniają się ”w tym samym kierunku”. W przypadku, gdy drożeje tylko jeden czynnik produkcji, oznacza to, że popyt na ten czynnik maleje, a gdy drożeje tylko jeden z produktów, wówczas jego podaż rośnie.

Można też wyprowadziś analogiczne prawo podaży dla dla odzworowania $\mathbf{y}$ nie będącego funkcją różniczkowalną.

Stwierdzenie 11.4

Niech $\mathbf{p\neq p}^{{\prime}}$ . Dla każdego $\mathbf{y}\in\mathbf{y}(\mathbf{p})$ i $\mathbf{y}^{{\prime}}\in\mathbf{y}(\mathbf{p}^{{\prime}})$ $(\mathbf{p-p}^{{\prime}})(\mathbf{y}-\mathbf{y}^{{\prime}})\geq 0$ z ostrą nierównością o ile $\mathbf{y}(\mathbf{p})\cap\mathbf{y}(\mathbf{p}^{{\prime}})=\emptyset$ .

Podobnie jak dowód stwierdzenia 6.5.

∎

11.2. Minimalizacja kosztów

W tym podrozdziale dla wygody skoncentrujemy się na naszym przypadku szczególnym, w którym mamy do czynienia z jednym produktem i funkcją produkcji.

Rozważmy sytuację, w której producent już ustalił, ile co najmniej musi wyprodukować (na przykład zawarł kontrakt). Jakie nakłady czynników poniesie firma maksymalizująca zysk?

Możemy też na zagadnienie, którym będziemy się teraz zajmować, spojrzeć też w inny sposób. W firmie jest dwóch specjalistów: od produkcji i od marketingu. Ten od produkcji wie, za ile najtaniej da się wyprodukować daną ilość produktu i jakie nakłady czynników trzeba zastosować. Nakłady czynników nie obchodzą specjalisty od marketingu, on chce tylko znać koszty. Tak więc musimy wyliczyć koszty dla najtańszego sposobu wyprodukowania $y$ .

W tej sytuacji producent jest zainteresowany, aby za produkcję przynajmniej tej ilości zapłacić jak najmniej. Jego zagadnienie optymalizacyjne ma postać: $\min _{{z\geq 0,\\ f(\mathbf{z})\geq y}}\mathbf{w}^{{T}}\mathbf{z}$ .

Definicja 11.1

Funkcję $c:\mathop{\rm{Int}}\mathbb{R}_{{+}}^{{n-1}}\times\mathbb{R}_{{+}}\rightarrow\mathbb{R}\cup\{+\infty\}$ , taką że $c(\mathbf{w},y)=\min _{{z\geq 0,\\ f(\mathbf{z})\geq y}}\mathbf{w}^{{T}}\mathbf{z}$ nazywamy funkcją kosztów, a odwzorowanie $\mathbf{z}:\mathop{\rm{Int}}\mathbb{R}_{{+}}^{{n-1}}\times\mathbb{R}_{{+}}\multimap\mathbb{R}_{{+}}^{{n-1}}$ , takie że $\mathbf{z}(\mathbf{w},y)=\mathop{\rm{Argmin}}_{{\mathbf{z}\geq 0,\\ f(\mathbf{z})\geq y}}\mathbf{w}^{{T}}\mathbf{z}$ – odwzorowaniem warunkowego popytu na czynniki produkcji.

Funkcja kosztów $c$ określa, ile co najmniej musimy zapłacić przy cenach czynników $\mathbf{w}$ , jeśli chcemy wyprodukować co najmniej $\mathbf{y}$ , a odwzorowanie $\mathbf{z}$ wskazuje optymalny zestaw czynników produkcji.

Ćwiczenie 11.2

Obliczyć funkcję zysku i odwzorowanie warunkowego popytu na czynniki produkcji dla technologii o wypisanych poniżej funkcjach produkcji.

a) Cobba-Douglasa $f(z_{1},z_{2})=z_{1}^{{a_{1}}}\cdot z_{2}^{{a_{2}}}$ dla $a_{i}>0$ ;

b) technologii liniowej $f(z_{1},z_{2})=z_{1}\cdot{a_{1}}+z_{2}\cdot{a_{2}}$ dla $a_{i}>0$ ;

c) technologii Leontiewa $f(z_{1},z_{2})=min\{ z_{1}\cdot{a_{1}},z_{2}\cdot{a_{2}}\}$ dla $a_{i}>0$ .

Ćwiczenie 11.3

Obliczyć funkcję zysku i odwzorowanie warunkowego popytu na czynniki produkcji dla technologii o funkcji produkcji $f(z_{1},z_{2})=min\{ z_{1}+2z_{2},z_{2}+2z_{1}\}$ .

Stwierdzenie 11.5

Minimalizacja kosztów jest warunkiem koniecznym maksymalizacji zysku: $\Pi([\mathbf{w},p]^{{T}})=\max _{{y\geq 0}}p\cdot y-c(\mathbf{w},y)$ .

Oczywiste.

∎

Jeśli przywołamy podział na specjalistę od marketingu i produkcji, i chcemy wytłumaczyć to bez użycia matematyki, to możemy inaczej to stwierdzenie sformułować jako ”można bezpiecznie rozdrobnić proces decyzyjny”. Jeśli specjalista od marketingu podejmie decyzję co do wielkości produkcji znając cenę i wyliczoną przez specjalistę od produkcji (bez znajomości ceny produktu) funkcję kosztów, to otrzymamy maksymalizację zysku.

Warunkiem konieczym minimalizacji kosztów przy różniczkowalnej funkcji $f$ jest: $w_{{l}}\geq\lambda\frac{\partial f(\mathbf{z}^{{*}})}{\partial z_{{l}}}$ z równością dla $z_{{l}}^{{*}}>0$ . Jeśli $f$ jest wklęsła, to jest to też warunek dostateczny. Stąd jeśli $z_{{l}},z_{{k}}>0$ , to $MRTS_{{l,k}}=-\frac{w_{{l}}}{w_{{k}}}$ .

Warto zauważyć analogię zagadnienia minimalizacji kosztów i zagadnienia minimalizacji wydatków w modelu konsumenta – matematycznie jest to to samo zagadnienie. Stąd większość własności $c$ i $\mathbf{z}$ będzie przeniesieniem własności $e$ i $h$ przy niemalejącej funkcji użyteczności.

Stwierdzenie 11.6

Własności funkcji kosztów i odwzorowania warunkowego popytu na czynniki produkcji mają dokładnie takie same własności jak $e$ i $h$ w modelu producenta (przenoszą się wszystkie włącznie z tymi noszącymi nazwą np. Lemat Shepharda).

Ćwiczenie 11.4

Czy funkcja $c(\mathbf{w},y)$ może być funkcją kosztów firmy maksymalizującej zysk? Jeśli tak, to wyliczyć funkcję zysku, odwzorowanie podaży i (przy założeniu, że to możliwe) odzworowanie warunkowego popytu na czynniki produkcji i uogólnione odwzrorowanie podaży.

a) $c(\mathbf{w},y)=\sqrt{y}\cdot(w_{1}\cdot w_{2})^{{\frac{3}{4}}}$ ;

b) $c(\mathbf{w},y)=y\cdot(w_{1}+\sqrt{w_{1}\cdot w_{2}}+w_{2}$ ;

c) $c(\mathbf{w},y)=y\cdot(w_{1}-\sqrt{w_{1}\cdot w_{2}}+w_{2}$ ;

d) $c(\mathbf{w},y)=(y+\frac{1}{y})\cdot\sqrt{w_{1}\cdot w_{2}}$ .

Oprócz własności rozważanych w modelu minimalizacji wydatków przez konsumenta, można dodatkowo udowodnić następujące własności, które w modelu producenta mają interpretację.

Stwierdzenie 11.7

a) Jeśli $f$ jest jednorodna stopnia $1$ to $c$ i $\mathbf{z}$ są jednorodne stopnia $1$ po $y$ ;

b) jeśli $f$ jest wklęsła, to $c$ jest wypukła po $y$ .

Ćwiczenie 11.5

Udowodnić stwierdzenie.

Ćwiczenie 11.6

Mając daną funkcję zysku i odwzorowanie warunkowego popytu na czynniki produkcji dla technologii o funkcjach produkcji Cobba-Douglasa, technologii liniowej i technologii Leontiewa z zadania 11.2, obliczyć jeszcze raz funkcję zysku oraz uogólnione odwzorowanie podaży.

W ekonomii używa się terminu koszt krańcowy na pochodną $c$ po $y$ (oznaczaną zazwyczaj przez $MC$ ), a koszt przeciętny na iloraz $c$ i $y$ (oznaczaną zazwyczaj przez $AC$ ); ceny czynników produkcji wówczas traktujemy jako ustalone. Wypukłość $c$ po $y$ oznacza, że koszt krańcowy jest niemalejący (jako funkcja $y$ ).

Wiemy, że minimalizacja kosztów jest warunkiem koniecznym maksymalizacji zysku, czyli $\Pi([\mathbf{w},p]^{{T}})=\max _{{y\geq 0}}p\cdot y-c(\mathbf{w},y)$ .

Stąd mamy jeszcze jeden warunek konieczny optymalizacji, tym razem przy użyciu funkcji kosztów: $p-\frac{\partial c(\mathbf{w},y^{{*}})}{\partial y}\leq 0$ , z równością gdy $y^{{*}}>0$ ; czyli dla $y^{{*}}>0$ cena jest równa kosztowi krańcowemu: $p=\frac{\partial c(\mathbf{w},y^{{*}})}{\partial y}$ .

11.2.1. Co można wydobyć z niepełnych danych

Przykład 11.1

Firma Aqq SA używa wciąż tej samej technologii o funkcji produkcji $f(x_{{1}},x_{{2}})$ .

Walne zgromadzenie akcjonariuszy ma rozważyć dalszy los zarządu, ale ma tylko niepełne dane: przy powielaniu sekretarce zagięła się kartka. Zasady są następujące: zmieniamy zarząd, jeśli z posiadanych danych wynika, że w którymś miesiącu postąpił nieracjonalnie; jeśli jesteśmy pewni, że zawsze maksymalizował zysk, pozostawiamy go; jeśli żadne z powyższych, musimy zażądać uzupełnienia danych i odłożyć decyzję do następnego walnego zgromadzenia.

Jaką decyzję powini podjąć akcjonariusze, jeśli te dane to:

	$w_{{1}}$	$w_{{2}}$	produkcja	koszty
styczeń	1	1	106	100
luty	2	2	105	200

	$w_{{1}}$	$w_{{2}}$	$x_{{1}}$	$x_{{2}}$	produkcja
styczeń	1	2	10	20	106
luty	1	1	15	15	105

Jedyne, co możemy zrobić, mając niepełne dane, to sprawdzić, czy wszystkie własności funkcji modelu są spełnione. Jeśli nie znamy zbioru dostępnych technologii ani funkcji produkcji, to nie możemy nigdy powiedzieć na pewno, że firma maksymalizowała zysk. Natomiast często możemy powiedzieć, że nie maksymalizowała.

a) Wiemy, że gdyby firma maksymalizowała zysk w obu okresach, to $c(1,1,106)=100$ i $c(2,2,105)=200$ . Z własności funkcji kosztów wiemy, że $c(2,2,106)=200$ (z jednorodności stopnia $1$ $c$ jako funkcji zmiennej $\mathbf{w}$ ), a ponieważ $c$ jest rosnąca jako funkcja wielkości produkcji $c(2,2,106)>c(2,2,105)=200$ co daje sprzeczność – zarząd trzeba zwolnić.

b) Tym razem mamy dane dwie technologie i ceny czynników produkcji. Aby stwierdzić, że firma nie maksymalizowała zysku, wystarczy pokazać, że gdyby zastosować technologię z jednego okresu przy cenach z drugiego okresu, moglibyśmy mieć większy zysk. Ponieważ nie mamy danych cen produktu, może się to udać jedynie, gdy przy tych samych kosztach uzyskamy większą produkcję lub gdy przy mniejszych kosztach uzyskamy tę samę produkcję. Taka sytuacja mogłaby nastąpić w lutym: koszty poniesione wyniosły $30$ i przy tych kosztach wyprodukowano $105$ jednostek produktu. Gdyby użyć technologii ze stycznia, to koszty wyniosłyby również $30$ , ale przy produkcji $106$ jednostek. Czyli znów zwalniamy zarząd.

11.2.2. Podział produkcji pomiędzy fabryki, kraje..

Jeśli mamy do czynienia z firmą posiadającą jedną fabrykę o określonej funkcji produkcji, wówczas funkcje modelu producenta możemy łatwo policzyć z definicji. A co jeśli firma ma więcej niż jedną fabrykę?

Przeanalizujemy sytaucję, gdy firma ma $m$ fabryk, być może w różnych krajach, w których są różne ceny czynników produkcji i chce podjąć decyzję, jak podzielić produkcję, w łącznej wielkości $y$ , pomiędzy nie. Funkcję produkcji $i$ -tej fabryki będziemy oznaczać przez $f_{{i}}(K,L)$ , a jej funkcję kosztów przez $c_{{i}}(\mathbf{w}^{{i}},y)$ , przy czym wektory cen czynników produkcji wszystkich fabryk $\mathbf{w}^{{i}}$ są dane.

Możemy zacząć analizę od początku, czyli od funkcji produkcji: wypisać łączną funkcję produkcji $m$ fabryk w zależności od $2m$ czynników produkcji i dalej mamy standartowe zagadnienie minimalizacji kosztów. Możemy jednak oszczędzić sobie liczenia i skorzystać z funkcji kosztów poszczególnych fabryk – nawet jeśli nie są one dane, obliczenie osobno funkcji kosztów fabryk, a potem rozwiązanie zagadnienia maksymalizacji zysku przy ich użyciu jest znacznie mniej złożone. Przy ograniczeniu, że łączna produkcja wynosi $y$ , minimalizujemy zatem łączne koszty, a więc mamy zagadnienie: $\min _{{y_{{1}}+y_{{2}}+\ldots+y_{{n}}=y}}\sum c_{{i}}(\mathbf{w}^{{i}},y_{{i}})$ .

Jeśli obliczymy warunki pierwszego rzędu, otrzymamy $\frac{\partial c_{{i}}(\mathbf{w}^{{i}},y_{{i}})}{\partial y_{{i}}}=\frac{\partial c_{{j}}(\mathbf{w}^{{j}},y_{{j}})}{\partial y_{{j}}}$ dla każdego $i$ , $j$ : koszty krańcowe w każdej fabryce muszą być równe. Równość ta ma, jak zwykle, proste sformułowanie łopatologiczne: nie opłaca się przenieść ”jednostki” produkcji z fabryki $i$ do fabryki $j$ ani na odwrót.

Uwaga! Jeśli rozważane fabryki mają rosnące przychody skali, to wyliczone w ten sposób rozwiązanie nie będzie maksimum, tylko minimum.

Ćwiczenie 11.7

Firma ma dwie fabryki o identycznych funkcjach produkcji w Polsce i Finlandii $f(K,L)=K^{{\frac{a}{2}}}\cdot L^{{\frac{a}{2}}}$ dla pewnego $a>0$ . Obliczyć, jak podzieli pomiędzy nie produkcję w wysokości $y$

a) przy identycznych cenach czynników produkcji w obu krajach $w_{1}=w_{2}=1$ ;

b) jeśli w Polsce $w_{1}^{P}=w_{2}^{P}=1$ , a w Finlandii $w_{1}^{F}=w_{2}^{F}=2$ .

Zagadnienie podziału produkcji pomiędzy fabryki może mieć nietypowe zastosowania, które na pierwszy rzut oka nie mają nic wspólnego z produkcją – w pewnych zagadnieniach ekologicznych.

Przykład 11.2

Kraje nadbałtyckie (jest ich $m$ ) postanowiły zmniejszyć zanieczyszczenia wpływające do Bałtyku o połowę. Zmniejszenie zanieczyszczeń kosztuje i łączny koszt jest pokrywany przez kraje w stosunku ustalonym w sposób niezależny od analizy kosztów (pewien rachunek korzyści). Wyprowadzić warunek konieczny minimalizacji łącznych kosztów zmniejszenia zanieczyszczeń o połowę, jeśli dla kraju $i$ -tego $c_{{i}}(q)$ oznacza koszt zmiejszenia zanieczyszczeń o $q\cdot 100\%$ , przy założeniu, że $c_{{i}}$ są funkcjami różniczkowalnymi, wypukłymi:

a) w przypadku gdy początkowo wszystkie kraje zrzucały do Bałtyku tyle samo zanieczyszczeń;

b) w przypadku gdy początkowe udziały krajów w łącznym zanieczyszczeniu są równe $a_{{i}}$ (dodatnie i sumują się do jedynki).

a) Wypiszemy zagadnienie optymalizacyjne: $\min _{{q_{{1}}+\cdots+q_{{m}}=50}}\sum _{{i=1}}^{{m}}c_{{i}}(q_{{i}})$ . Otrzymamy warunek konieczny jak w przypadku podziału produkcji między fabryki: $\frac{\partial c_{{i}}(\mathbf{w}^{{i}},y_{{i}})}{\partial y_{{i}}}=\frac{\partial c_{{j}}(\mathbf{w}^{{j}},y_{{j}})}{\partial y_{{j}}}$ dla każdego $i$ , $j$ .

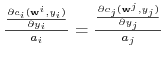b) Tym razem zagadnienie optymalizacyjne ma postać: $\min _{{a_{{1}}\cdot q_{{1}}+\cdots+a_{{m}}\cdot q_{{m}}=50}}\sum _{{i=1}}^{{m}}c_{{i}}(q_{{i}})$ . Otrzymany warunek konieczny ma postać: $\frac{\frac{\partial c_{{i}}(\mathbf{w}^{{i}},y_{{i}})}{\partial y_{{i}}}}{a_{{i}}}=\frac{\frac{\partial c_{{j}}(\mathbf{w}^{{j}},y_{{j}})}{\partial y_{{j}}}}{a_{{j}}}$ dla każdego $i$ , $j$ .

Co ciekawe, takie analizy zostały rzeczywiście przeprowadzone w latach dziewięćdziesiątych. Interesujące są zwłaszcza przepływy netto pomiędzy krajami. Jak należało oczekiwać, zasadniczo kraje lepiej rozwinięte zmniejszały emisję o mniej niż $50\%$ i płaciły krajom gorzej rozwiniętym, które zmniejszały emisję o więcej niż pięćdziesiąt procent. Wytłumaczenie jest proste – koszty krańcowe dla tej samej wielkości $q$ są większe dla krajów bogatszych, używających już znacznie bardziej przyjaznych środowisku technologii: na przykład w Warszawie można wybudować oczyszczalnię ścieków, podczas gdy Kopenhaga już taką oczyszczalnię posiada i spuszcza ścieki, których dalsze oczyszczenie byłoby bardzo kosztowne. Podobnie wygląda sprawa z kosztami przestawienia na mniej szkodliwą produkcję. Od generalnej zasady były tylko dwa wyjątki, z których jeden związany jest z niniejszą analizą: Rosja podzieliła los krajów bogatych – wówczas jej gospodarka była na tyle nieefektywna, że zmniejszenie zanieczyszczeń okazało się praktycznie niewykonalne.

11.2.3. Krótki i długi okres dla producenta

Terminy ”krótki okres”, ”średni okres” i ”długi okres” w teorii ekonomii nie mają jednoznacznej definicji. Po pierwsze, co innego będzie krótkim okresem w modelu producenta, a co innego w modelu rynku. Mimo tego te pojęcia, a zwłaszcza pierwsze i ostatnie, są bardzo często używane. Jeśli ograniczymy się do modelu producenta, nadal nie mamy definicji w dniach czy miesiącach. Granica pomiędzy krótkim a długim okresem, zmienia się w zależności od rodzaju produkcji: dla rolnika trzy miesiące będzie przeważnie krótkim okresem, zwłaszcza pomiędzy kwietniem a lipcem, a dla chałupniczego producenta wełnianych skarpet będzie to zapewne okres długi. Długość okresu określa ilość ustalonych nakładów czynników produkcji: w najdłuższym możliwym okresie, jak w naszych wcześniejszych analizach, wszystkie nakłady czynników produkcji są zmienne. Tak więc powyższa analiza zachowania producenta opisuje analizę zachowania producenta w długim okresie. Im krótszy okres, tym więcej czynników produkcji będzie ustalonych: umowy na dzierżawę kapitału podpisuje się np. na pół roku, a nawet na rok, natomiast szybciej można zwolnić pracowników lub przyjąć nowych (w warunkach polskich praca nie jest aż tak mobilna, przynajmniej jeśli chodzi o zatrudnionych legalnie, ale np. w Stanach Zjednoczonych średni okres wypowiedzenia wynosi dwa dni! – to też określa długość krótkiego okresu). Generalnie przy dwóch czynnikach produkcji, krótki okres to taki, w którym tylko praca jest zmienna, a kapitał ustalony. Uwaga: w analizie działania rynku pojęcia długości okresu nieco się zmienią, żeby pomieścić jeszcze sytuacje skrajne, które nie są interesujące z punktu widzenia producenta: okres na tyle krótki, że wszystko jest ustalone i okres na tyle długi, aby mogły powstać nowe firmy albo stare upaść.

W krótkim i średnim okresie występują więc koszty stałe i koszty zmienne. W tej sytaucji zagadnienie minimalizacji kosztów ma postać: $\min _{{\mathbf{z}\geq 0,\\ f(\mathbf{z})\geq y\\ z_{{i}}=\bar{z}_{{i}}\text{ dla }i\in\Phi}}\mathbf{w}^{{T}}\mathbf{z;}$ gdzie $\Phi$ oznacza zbiór indeksów, dla których nakład czynnika jest ustalony.

Definicja 11.2

Jeżeli w krótkim okresie dla $i\in\Phi$ $z_{{i}}=\bar{z}_{{i}}$ , to funkcję $c^{{S}}:\mathop{\rm{Int}}\mathbb{R}_{{+}}^{{n-1}}\times\mathbb{R}_{{+}}\rightarrow\mathbb{R}\cup\{+\infty\}$ , taką że $c(\mathbf{w},y)=\min _{{z\geq 0,\text{ }f(\mathbf{z})\geq y\\ z_{{i}}=\bar{z}_{{i}}\text{ dla }i\in\Phi}}\mathbf{w}^{{T}}\mathbf{z}$ nazywamy krótkookresową funkcją kosztów, a odwzorowanie $\mathbf{z}^{{S}}:\mathop{\rm{Int}}\mathbb{R}_{{+}}^{{n-1}}\times\mathbb{R}_{{+}}\multimap\mathbb{R}_{{+}}^{{n-1}}$ , takie że $\mathbf{z}(\mathbf{w},y)=\mathop{\rm{Argmin}}_{{z\geq 0,\text{ }f(\mathbf{z})\geq y\\ z_{{i}}=\bar{z}_{{i}}\text{ dla }i\in\Phi}}\mathbf{w}^{{T}}\mathbf{z}$ – krótkookresowym odwzorowaniem warunkowego popytu na czynniki produkcji. Koszt stały to $\bar{c}^{{S}}=\sum _{{i\in\Phi}}w_{{i}}z_{{i}}$ , a koszt zmienny $c^{{S}}-\bar{c}^{{S}}$ .

Analogicznie definiujemy krótkookresowe ogólne odwzorowanie podaży $\mathbf{y}^{{S}}(\mathbf{p})=\mathop{\rm{Argmax}}_{{\mathbf{y}\in\mathbb{Y}\\ y_{{i}}=-\bar{z}_{{i}}\text{ dla }i\in\Phi}}\mathbf{p}^{{T}}\mathbf{y}$ i krótkookresową funkcję zysku: $\Pi^{{S}}(\mathbf{p})=\max _{{\mathbf{y}\in\mathbb{Y}\\ y_{{i}}=-\bar{z}_{{i}}\text{ dla }i\in\Phi}}\mathbf{p}^{{T}}\mathbf{y}$ .

Ćwiczenie 11.8

Firma wolno-konkurencyjna MacroHard ma dwie fabryki o identycznych funkcjach produkcji $f(K,L)=(KL)^{{\frac{1}{4}}}$ , ulokowane w Polsce, gdzie cena jednostki kapitału wynosi $10$ , a cena pracy $5$ i w Chinach, gdzie cena kapitału wynosi $5$ , a cena pracy $1$ . Firma ma wyprodukować $10$ jednostek produktu. Jak podzieli produkcję pomiędzy fabryki, jakie będą nakłady czynników produkcji w każdej z nich i koszty

a) w długim okresie;

b) w krótkim okresie, kiedy w Chinach firma ma $0$ jednostek kapitału, a w Polsce $10$ .

Stwierdzenie 11.8 (Zasada le Chateliera)

Rozważmy przypadek szczególny o różniczkowalnej funkcji $f$ i wektor czynników produkcji $\bar{z}=z(\mathbf{w},\bar{p})$ . Jeśli zarówno podaż produktu $y$ jak i podaż krótkookresowa $y^{{S}}$ są funkcjami różniczkowalnymi ściśle dodatnimi w otoczeniu $(\mathbf{w},\bar{p})$ , to $\frac{\partial y(\mathbf{w},\bar{p})}{\partial p}-\frac{\partial y^{{S}}(\mathbf{w},\bar{p})}{\partial p}\geq 0$ . (Zmiana podaży produktu pod wpływem zmiany jego ceny w długim okresie jest co najmniej tak samo duża jak w krótkim.)

Ponieważ zagadnienie maksymalizacji zysku krótkookresowe jest zagadnieniem na mniejszym zbiorze, więc, oczywiście, $\Pi(\mathbf{w},p)-\Pi^{{S}}(\mathbf{w},p)\geq 0$ dla każdego $\mathbf{w}$ , $p$ z równością dla $p=\bar{p}$ . Z tego wynika, że w $\bar{p}$ jest przyjmowane minimum funkcji $\Pi(\mathbf{w},p)-\Pi^{{S}}(\mathbf{w},p)$ po $p$ , a więc druga pochodna tego wyrażenia (która istnieje z lematu Hotellinga 11.3) musi być nieujemna. Z lematu Hotellinga jest ona równa $\frac{\partial^{{2}}\left(\Pi(\mathbf{w},\bar{p})-\Pi^{{S}}(\mathbf{w},\bar{p})\right)}{\partial p^{{2}}}=\frac{\partial y(\mathbf{w},\bar{p})}{\partial p}-\frac{\partial y^{{S}}(\mathbf{w},\bar{p})}{\partial p}\geq 0$ .

∎

Analogicznie można pokazać, że im dłuższy okres, tym bardziej zmienia się podaż w reakcji na zmianę ceny produktu.

Warto zauważyć, że o ile w długim okresie produkujemy tylko jeśli zysk z pewnego niezerowego poziomu produkcji jest nieujemny, o tyle w krótkim okresie możemy produkować przy ujemnym zysku, czyli stracie: o ile strata jest mniejsza niż koszt stały, czyli utarg ze sprzedaży produkcji $py$ jest większy niż koszt zmienny produkcji $y$ .

Warunkiem zaprzestania produkcji w krótkim okresie jest: dla każdego $y>0$ zachodzi nierówność $py<c^{{S}}(y)-\bar{c}^{{S}}$ – utarg ze sprzedaży produkcji nie pokrywa kosztów zmiennych.

Jeszcze jedna uwaga dotycząca kosztów. Koszty z punktu widzenia ekonomisty to coś zupełnie innego niż koszty księgowe (faktyczne dokonane i uwiecznione w dokumentach przepływy wypłat z tytułu użytkowania czynników produkcji oraz odliczenia na amortyzację). Drobny rolnik, który pracę wykonuje sam, na własnej działce, inwestuje własne pieniądze na nasiona i używa własnej łopaty (księgowość wykazałaby jedynie koszty zakupu nasion i ewentualnie amortyzację łopaty) ponosi takie same koszty, jak gdyby pożyczył pieniądze na nasiona z banku, zapłacił za dzierżawę cudzej działki i wynajem łopaty oraz zatrudnił pracownika. Dzieje się tak dlatego, że posiadane pieniądze mógłby np. komuś pożyczyć albo ulokować w banku (za co uzyskałby odsetki), działkę mógłby wydzierżawić, a w czasie, kiedy pracuje ”dla siebie” mógłby zarobić pieniądze w innej firmie. Te koszty trzeba wziąć pod uwagę. Są to tak zwane koszty alternatywne albo koszty poniechanych możliwości. W analizie decyzji ekonomicznych nie mają natomiast znaczenia już poniesione koszty, których nie można odzyskać – są to koszty utopione – analizujemy tylko obecne i przyszłe koszty (faktyczne i alternatywne).

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Skrypt do wykładu z mikroekonomii dla wydziału MIMUW 2009/2010