12. Rynek wolnokonkurencyjny – równowaga cząstkowa
Teraz zajmiemy się połączeniem teorii konsumpcji i produkcji. Konsumenci dóbr i ich producenci spotykają sią na rynku, który ustala ceny. Zaczniemy od najprostszego ujęcia zagadnienia – podejścia równowagi cząstkowej. Polega ono na tym, że analizujemy jedynie rynek jednego dobra rozpatrywany niezależnie od innych (możemy tak postępować, jeśli już policzyliśmy funkcje popytu, podaży i kosztów uczestników rynku, i zakładamy, że wszystkie ceny pozostałych dóbr nie zmieniają się – jest to założenie nieco wygórowane). Na tym poziomie wszystkie informacje o konsumentach czerpiemy z ich funkcji popytu na to dobro, a o producentach z ich funkcji podaży produktu i funkcji kosztów. Na tej podstawie będziemy mogli opisać skąd się biorą i jak ewoluują ceny.
Tak więc rozważamy tylko abstrakcyjny rynek jednego, ustalonego
dobra (powiedzmy ![]() -tego), nie interesując się pozostałymi. Mamy
zbiór
-tego), nie interesując się pozostałymi. Mamy
zbiór ![]() konsumentów tego dobra i zbiór
konsumentów tego dobra i zbiór ![]() jego
producentów – oba te zbiory są w naszej analizie skończone.
jego
producentów – oba te zbiory są w naszej analizie skończone.
Przy ustalonych cenach pozostałych dóbr i dochodzie konsument ![]() ma
fukcję popytu na dobro
ma
fukcję popytu na dobro ![]()
![]() .
.
Przy ustalonych cenach pozostałych dóbr (w tym czynników
produkcji), producent ![]() ma funkcję podaży dobra
ma funkcję podaży dobra ![]()
![]() , a jeśli jest producentem jedynie dobra
, a jeśli jest producentem jedynie dobra ![]() , także
funkcję kosztów
, także
funkcję kosztów ![]() .
.
Jesteśmy na rynku wolnokonkurencyjnym. Przetłumaczone na sytuację rzeczywistą, oznacza to, że wybór zarówno producentów jak i konsumentów jest podyktowany jedynie względami ekonomicznymi (nie ma zakazów ani nakazów), nie ma kosztów wejścia na rynek ani wyjścia z rynku, wszyscy uczestnicy dysponują pełną informacją o cenach: konsumenci o cenach dyktowanych przez różnych producentów (stąd nikt nie kupi po wyższej cenie niż najniższa oferowana; producent nie może więc podnosić ceny powyżej ceny rynkowej, bo nie sprzeda produkcji, a zakładamy, że zawsze zauważy, że popyt wzrósł i można podnieść cenę do nowej ceny rynkowej) oraz że to samo dobro produkowane przez różnych producentów jest postrzegane identycznie przez konsumentów. Jest to model idealny (jak np. modele ruchu bez tarcia w fizyce), ale całkiem nieźle modeluje rzeczywiste prawie konkurencyjne rynki (np. wspomniany już rynek gwoździ na Grzybowskiej albo giełdę kwiatową, ale już nie rynek samochodowy – tu marka gra rolę).
Te wszystkie elementy opisu można zastąpić dwoma założeniami: jedynym parametrem wpływającym na wybór są ceny dóbr i ceny dóbr są traktowane jako dane. Zakładamy, że wszystkie parametry poza ceną naszego dobra są ustalone.
Definicja 12.1
Funkcją popytu rynkowego na dobro ![]() nazywamy funkcję
nazywamy funkcję
![]() .
.
Funkcją podaży rynkowej (albo funkcją podaży gałęzi) dobra ![]() nazywamy funkcję
nazywamy funkcję ![]() .
.
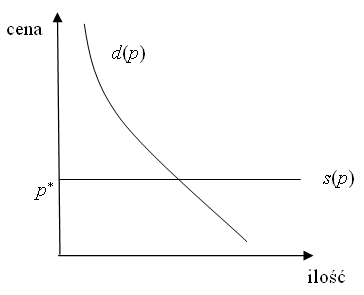
Równowagą nazywamy taki stan rynku (tj. ![]() – cenę, konsumpcję i produkcję), że
– cenę, konsumpcję i produkcję), że ![]() (podaż równa się popytowi). Taka
cena
(podaż równa się popytowi). Taka
cena ![]() jest nazywana ceną równowagi i wyznacza ona
wszystkie pozostałe zmienne.
jest nazywana ceną równowagi i wyznacza ona
wszystkie pozostałe zmienne.
Uwaga do ewentualnych wykresów: ze względu na tradycję ekonomiści rysują osie w wykresach popytu i podaży na odwrót – cena na pionowej, ilość na poziomej (czyli w rzeczywistości to, co rysujemy, będzie odwrotną funkcją popytu i podaży). Przyjmiemy tę konwencję, gdyż chyba nie ma książki, w której byłoby inaczej.
12.1. Krótki i długi okres dla rynku
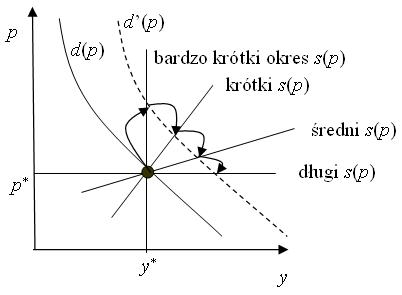
Podobnie jak w przypadku podaży firmy, tak i podaż gałęzi może być z definicji długo-, średnio- albo krótko-okresowa. Tak więc sytuacja na rynku, a co za tym idzie równowaga też może być zależna od długości okresu. Tu określenia długości będą miały nieco inne znaczenie.
Znów nie ma tu precyzyjnej definicji długości okresu. Generalnie im krótszy okres, tym większa liczba czynników ustalona, co wpływa na postać funkcji podaży – im dłuższy okres, tym bardziej zmienna; ponadto z upływem czasu może pojawiać się coraz więcej kopii dobrze prosperującej firmy, natomiast coraz więcej firm mających straty upada. W naszych rozważaniach przyjmiemy następujący podział:
przez bardzo krótki okres będziemy rozumieć taki, w którym wszystkie czynniki ustalone, a więc produkcja ustalona;
krótki okres – pewna część czynników produkcji
ustalona, zbiór ![]() ustalony – nie powstają ani nie upadają
firmy, firmy mogą produkować nawet przy ujemnym zysku, jeśli z
utargu pokrywają przynajmniej koszty zmienne;
ustalony – nie powstają ani nie upadają
firmy, firmy mogą produkować nawet przy ujemnym zysku, jeśli z
utargu pokrywają przynajmniej koszty zmienne;
średni okres – wszystkie czynniki produkcji zmienne, istnieje
tylko koszt stały istnienia firmy, zbiór ![]() ustalony, firmy produkują tylko jeśli zysk nieujemny (zakładamy że produkują
też przy zysku
ustalony, firmy produkują tylko jeśli zysk nieujemny (zakładamy że produkują
też przy zysku ![]() );
);
długi okres – wszystko zmienne; powstają kopie firmy przynoszącej zysk dodatni, upadają firmy przynoszące stratę.
Zakładamy, że wszystkie rozważane funkcje są gładkie,
funkcje kosztów są wypukłe, koszty krańcowe dążą
do nieskończoności przy produkcji dążącej do
nieskończoności, koszty przeciętne i koszty przeciętne
zmienne mają kształt litery ![]() .
.
Stwierdzenie 12.1
Funkcje podaży dążą z czasem do (poziomej przy założeniu, że osie są na odwrót!) prostej, zwanej funkcją długookresowej podaży gałęzi (w naszym rozumieniu nie
jest to funkcja), gdzie cena równa się kresowi dolnemu zbioru
minimów kosztów przeciętnych (![]() ). Wówczas wszyscy producenci mają zysk równy
). Wówczas wszyscy producenci mają zysk równy
![]() i każdy z nich produkuje na poziomie
i każdy z nich produkuje na poziomie ![]() , a liczba firm jest taka, żeby popyt był równy
podaży.
, a liczba firm jest taka, żeby popyt był równy
podaży.
Jak to działa w rzeczywistości, czyli coś w rodzaju dowodu:
Niech ![]() firma taka, że
firma taka, że ![]() i to minimum jest przyjmowane dla
i to minimum jest przyjmowane dla ![]() .
.
Jeśli ![]() , to z czasem pojawiają się kopie firmy
, to z czasem pojawiają się kopie firmy ![]() , bo
osiąga ona dodatnie zyski i największe ze wszystkich firm, ale popyt
się nie zmienił, więc cena musi spaść, gdyż inaczej
producenci zostaliby z towarem. Jeśli natomiast
, bo
osiąga ona dodatnie zyski i największe ze wszystkich firm, ale popyt
się nie zmienił, więc cena musi spaść, gdyż inaczej
producenci zostaliby z towarem. Jeśli natomiast ![]() , to wszystkie
firmy przynoszą stratę. W długim okresie część z nich
zaprzestanie produkcji i rozwiąże się, a więc przy tym samym
popycie spadnie podaż. Stąd cena musi wzrosnąć, gdyż
konsumenci są skłonni zapłacić więcej, byle tylko dostać
brakujące dobro.
, to wszystkie
firmy przynoszą stratę. W długim okresie część z nich
zaprzestanie produkcji i rozwiąże się, a więc przy tym samym
popycie spadnie podaż. Stąd cena musi wzrosnąć, gdyż
konsumenci są skłonni zapłacić więcej, byle tylko dostać
brakujące dobro.
Czyli w długim okresie to funkcja produkcji najlepszej technologii (a dokładniej jej funkcja kosztów) determinuje cenę równowagi ![]() , każda z firm będzie produkować
, każda z firm będzie produkować ![]() gdzie
gdzie ![]() – firma stosująca
najlepszą technologię, a firm będzie tyle by zaspokoić popyt.
– firma stosująca
najlepszą technologię, a firm będzie tyle by zaspokoić popyt.
W bardzo krótkim okresie przeciwnie – jedynie popyt determinuje
równowagę (bo podaż ustalona). Ma to miejsce w sytuacji, gdy
przy ustalonej produkcji następuje tzw. szok popytowy: pozytywny, czyli skokowe, nieprzewidziane zwiększenie popytu (np.
miasto zostaje zamknięte z powodu epidemii lub oblężenia i
ludzie zaczynają w panice kupować żywność; do
niewielkiego miasta sprowadzają się imigranci itp.) lub negatywny (jak np. informacja o wściekłych krowach na rynku wołowiny). Jeżeli jest dokładnie ![]() towaru na rynku, to ustali się
cena
towaru na rynku, to ustali się
cena ![]() , taka że
, taka że ![]() (w bardzo krótkim okresie funkcja
podaży jest na wykresie pionowa – znów uwaga na osie).
(w bardzo krótkim okresie funkcja
podaży jest na wykresie pionowa – znów uwaga na osie).
Im dłuższy okres, tym krzywa podaży jest bardziej płaska, coraz mniejszy wpływ na cenę ma popyt. Najpierw już istniejące firmy zwiększają lub zmniejszają zatrudnienie kolejnych czynników, które stały się zmienne. Potem powstają nowe firmy albo upadają istniejące. Z czasem cena wróci do poprzedniej ceny równowagi długookresowej, przy tej samej produkcji pojedynczych firm, jedynie przy większej ilości firm.
Przykład 12.1
Mamy rynek w równowadze długookresowej, na którym działają
tylko firmy o funkcji produkcji Cobb-Douglasa ![]() , o kosztach stałych działalności
, o kosztach stałych działalności ![]() ,
ceny czynników wynoszą
,
ceny czynników wynoszą ![]() i
i ![]() . Funkcja
popytu to
. Funkcja
popytu to ![]() .
.
Jak łatwo policzyć, w krótkim okresie (![]() ,
, ![]() zmienne)
funkcja kosztów ma postać
zmienne)
funkcja kosztów ma postać
![]() , a w długim okresie
, a w długim okresie ![]() .
.
W równowadze długookresowej cena na rynku równa jest ![]() , każda z firm produkuje
, każda z firm produkuje ![]() , przy nakładach
, przy nakładach ![]() i
i ![]() . Ponieważ popyt wynosi
. Ponieważ popyt wynosi ![]() , więc na rynku jest
, więc na rynku jest ![]() aktywnych firm.
aktywnych firm.
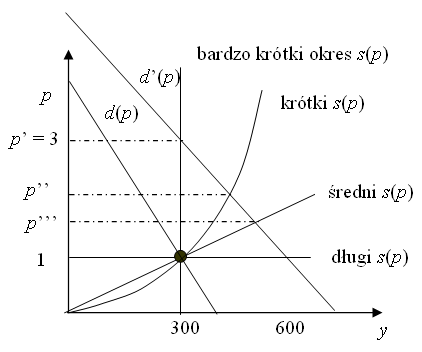
Teraz zobaczmy, co się stanie, jeśli do miasta sprowadzą się
nowi mieszkańcy, co zwiększy popyt do ![]() .
.
W bardzo krótkim okresie podaż jest ![]() , więc
, więc ![]() ,
więc cena ustali się na
,
więc cena ustali się na ![]() . W krótkim okresie
można zwiększyć produkcję zwiększając zatrudnienie
pracy.
. W krótkim okresie
można zwiększyć produkcję zwiększając zatrudnienie
pracy.
Krótkookresowa funkcja kosztów ma postać ![]() a więc każda firma jest skłonna wyprodukować
a więc każda firma jest skłonna wyprodukować ![]() , czyli
, czyli ![]() . Stąd
funkcja podaży gałęzi to
. Stąd
funkcja podaży gałęzi to ![]() . W
równowadze krótkookresowej
. W
równowadze krótkookresowej ![]() co
wyznacza cenę
co
wyznacza cenę ![]() .
.
W średnim okresie na rynku jest nadal 900 aktywnych firm o funkcji
kosztów ![]() i produkcja każdej równa się
i produkcja każdej równa się ![]() , czyli
, czyli ![]() . Stąd
. Stąd ![]() W równowadze średniookresowej
W równowadze średniookresowej ![]() , co
wyznacza cenę
, co
wyznacza cenę ![]() .
.
W długim okresie cena znów jest ![]() , każda z firm produkuje
, każda z firm produkuje ![]() , przy nakładach
, przy nakładach ![]() i
i ![]() i ma zerowy
zysk. Ponieważ popyt wynosi
i ma zerowy
zysk. Ponieważ popyt wynosi ![]() , więc na rynku jest
, więc na rynku jest ![]() aktywnych firm.
aktywnych firm.
Uwaga 12.1
To, że zysk w równowadze w długim okresie jest zerowy nie jest bezsensowne: oznacza to, że przychód jest równy kosztom. Przypomnijmy jednak, że bierzemy pod uwagę koszty alternatywne. Zerowy zysk oznacza jedynie, że jeśli zainwestujemy w naszą działalność, to uzyskamy tyle samo jak przy najlepszej możliwej innej inwestycji (np. właściciel firmy zarabia za swoją pracę tyle samo ile uzyskałby jako prezes na państwowej posadzie).
Ćwiczenie 12.1
Podzespoły elektroniczne są produkowane w branży
doskonale konkurencyjnej przy pomocy jednej z dwóch technologii o
funkcjach kosztów długookresowych odpowiednio ![]() i
i ![]() . Obliczyć jakie będą
parametry równowagi długookresowej (liczba firm stosujących
każdą z technologii, produkcja każdej firmy, produkcja łączna i cena), jeśli funkcja popytu jest równa
. Obliczyć jakie będą
parametry równowagi długookresowej (liczba firm stosujących
każdą z technologii, produkcja każdej firmy, produkcja łączna i cena), jeśli funkcja popytu jest równa ![]() .
Opisać proces dochodzenia do tej równowagi, jeśli początkowo
cena jest równa
.
Opisać proces dochodzenia do tej równowagi, jeśli początkowo
cena jest równa ![]() i istnieją firmy posługujące się
każdą z tych technologii (zmianę technologii traktujemy jako
likwidację starej firmy i założenie nowej).
i istnieją firmy posługujące się
każdą z tych technologii (zmianę technologii traktujemy jako
likwidację starej firmy i założenie nowej).
Co jeśli konkurencja nie jest doskonała: np mamy licencje (za które trzeba zapłacić) na taksówki, sprzedaż alkoholu albo administracyjne utrudnienia w konkurencji (np. urzędnik oczekuje łapówki)?
Każda firma patrzy, czy opłaca jej się wejść na rynek. Nawet jeśli zysk jest dodatni to może nie wystarczyć na pokrycie kosztu wejścia na rynek. Wówczas firmy, które już są na rynku mogą mieć wysokie zyski nawet w długim okresie – możemy je określić jako ekonomiczną ”rentę z bycia pierwszym”. Jeśli jakaś firma zdecyduje się sprzedać swoją licencję, to za cenę przynajmniej równą zdyskontowanemu strumieniowi przyszłych dochodów (przy założeniu doskonałego rynku kredytów i doskonałej informacji), a wchodząca firma nie da więcej.
12.1.1. Skutki opodatkowania – przykład analizy
Załóżmy, że jesteśmy w równowadze długookresowej. Rząd, chcąc zwiększyć wpływy do budżetu, nakłada
podatek na produkt produkowany przez firmy doskonale konkurencyjne: w kwocie
![]() od jednostki. Jakie będą tego skutki?
od jednostki. Jakie będą tego skutki?
Wszystko jedno, przez kogo fizycznie jest płacony podatek i czy jest wliczony w cenę, rezultat będzie taki sam: zmiejszenie produkcji.
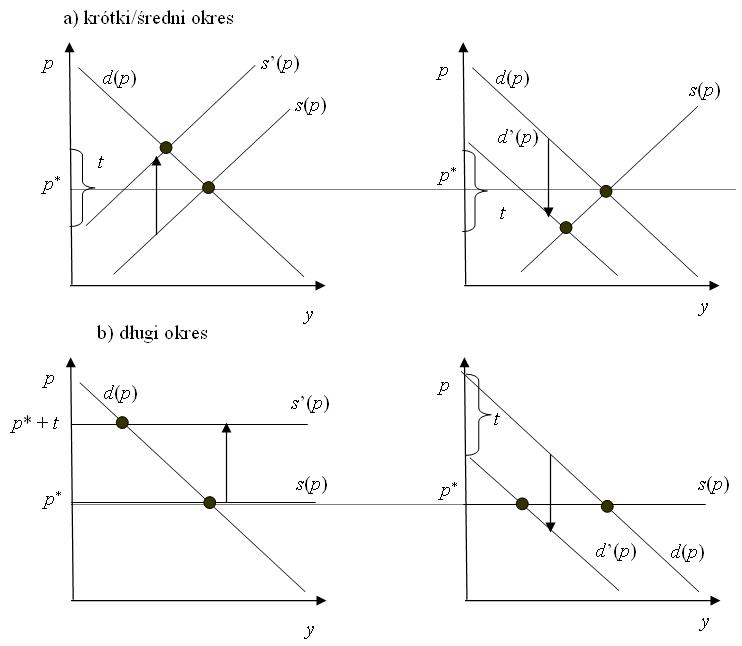
Jeżeli podatek jest wliczony w cenę i płaci go producent,
wówczas przy cenie rynkowej ![]() , podaż producenta jest równa
, podaż producenta jest równa
![]() (to oznacza przesunięcie krzywej podaży o
(to oznacza przesunięcie krzywej podaży o ![]() w górę), a popyt się nie zmienia. W bardzo krótkim okresie cena nie
zmieni się, czyli cały ciężar podatku ponoszą producenci.
Z czasem cena będzie wzrastać, a podaż maleć, a udział
konsumentów w płaceniu podatku wzrastać, aż w długim okresie
cena będzie wynosić
w górę), a popyt się nie zmienia. W bardzo krótkim okresie cena nie
zmieni się, czyli cały ciężar podatku ponoszą producenci.
Z czasem cena będzie wzrastać, a podaż maleć, a udział
konsumentów w płaceniu podatku wzrastać, aż w długim okresie
cena będzie wynosić ![]() , czyli cały ciężar podatku
spada na konsumentów.
, czyli cały ciężar podatku
spada na konsumentów.
Jeżeli podatek nie jest wliczony w cenę i płaci go konsument,
wówczas przy cenie rynkowej ![]() , podaż producenta nie zmienia się a popyt jest równy
, podaż producenta nie zmienia się a popyt jest równy ![]() (ważne jest, ile łącznie
muszę zapłacić, kupując dobro; to oznacza przesunięcie
krzywej popytu o
(ważne jest, ile łącznie
muszę zapłacić, kupując dobro; to oznacza przesunięcie
krzywej popytu o ![]() w dół). W bardzo krótkim okresie podaż
nie zmieni się, więc cena musi spaść od
w dół). W bardzo krótkim okresie podaż
nie zmieni się, więc cena musi spaść od ![]() , czyli
cały ciężar podatku ponoszą producenci. Z czasem cena będzie wzrastać i podaż maleć, a udział konsumentów w płaceniu podatku wzrastać, aż w długim okresie cena będzie
wynosić
, czyli
cały ciężar podatku ponoszą producenci. Z czasem cena będzie wzrastać i podaż maleć, a udział konsumentów w płaceniu podatku wzrastać, aż w długim okresie cena będzie
wynosić ![]() , czyli cały ciężar podatku spada na
konsumentów.
, czyli cały ciężar podatku spada na
konsumentów.
W obu sytuacjach zysk każdego producenta i faktyczna cena płacona przez konsumenta za dobro jest taka sama.
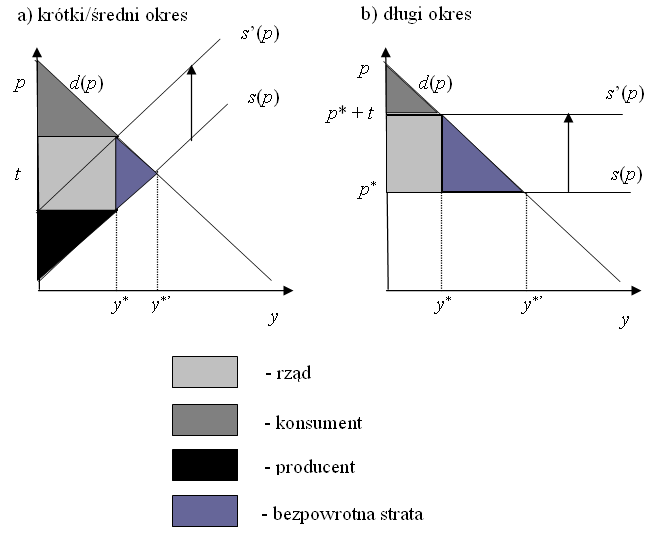
Zobaczmy teraz jak w średnim i długim okresie wpływy podatkowe maja się do tego, co tracą uczestnicy rynku. Dla ustalenia uwagi
przyjmijmy, że to producent płaci podatek. W obu sytuacjach produkcja
się zmniejsza, a więc wpływy rządu z podatków (pole prostokąta o bokach ![]() i
i ![]() ) są mniejsze niż to, co tracą łącznie konsumenci i producenci : zmniejszenie sumy ich nadwyżek
(nadwyżka konsumentów przy cenie
) są mniejsze niż to, co tracą łącznie konsumenci i producenci : zmniejszenie sumy ich nadwyżek
(nadwyżka konsumentów przy cenie ![]() to pole figury pomiędzy
krzywą popytu a poziomą prostą na wysokości płaconej ceny
to pole figury pomiędzy
krzywą popytu a poziomą prostą na wysokości płaconej ceny ![]() aż do przecięcia popytu z podażą, a producenta pole
figury pomiędzy prostą poziomą na wysokości otrzymywanej
ceny netto:
aż do przecięcia popytu z podażą, a producenta pole
figury pomiędzy prostą poziomą na wysokości otrzymywanej
ceny netto: ![]() przed podatkiem,
przed podatkiem, ![]() po, a krzywą podaży aż do
przecięcia krzywych popytu i podaży).
po, a krzywą podaży aż do
przecięcia krzywych popytu i podaży).
Ćwiczenie 12.2
Rynek płynów mrozoodpornych do spryskiwaczy w Polsce jest
doskonale konkurencyjny i obecnie jest w stanie rónowagi długookresowej. Działające na nim firmy mają technologię o
funkcji kosztów, przy ustalonych na obecnym poziomie cenach czynników produkcji, ![]() .
.
a) Obliczyć parametry tej równowagi jeśli funkcja popytu to ![]() .
.
b) Rząd postanowił wprowadzić podatek, w wysokości ![]() zł od
butelki, motywując to dofinansowaniem funduszu przeciwdziałania
alkoholizmowi. Co się będzie działo:
zł od
butelki, motywując to dofinansowaniem funduszu przeciwdziałania
alkoholizmowi. Co się będzie działo:
(i) w bardzo krótkim okresie (od razu po wprowadzeniu podatku, gdy produkcja jest jeszcze ustalona);
(ii) w krótkim okresie, gdy koszty produkcji są postaci
![]() , gdzie
, gdzie ![]() to wielkość produkcji ustalona wcześniej (obliczona w punkcie a);
to wielkość produkcji ustalona wcześniej (obliczona w punkcie a);
(iii) w średnim okresie (gdy liczba firm jest ustalona);
(iv) w długim okresie.