14. Modele równowagi ogólnej
W przedstawionych tu prostych modelach równowagi ogólnej nie stosujemy sztucznego podziału na odrębne rynki, lecz badamy rynek jako całość. Interesują nas równowagi, jednakże nie analizujemy procesu dochodzenia do równowagi, a jedynie kwestię jej istnienia i własności.
14.1. Model czystej wymiany towarowej
Zaczniemy od analizy sytuacji, w której nie ma producentów – dobra
już zostały wyprodukowane i pewne ich koszyki są w posiadaniu
konsumentów. Ponieważ jest to w odniesieniu do obecnych rynków
sytuacja raczej nietypowa (gracze mają i chcą uzyskać pewne
koszyki dóbr, a w tym modelu nie możemy traktować pieniądza
jako jednego z dóbr o ustalonej cenie ![]() ), aby łatwiej było o
intuicję, wyobraźmy sobie imprezę składkową – każdy z
jej uczestników przynosi pewien koszyk dóbr (jeden kiełbaski,
drugi chleb i musztardę, trzeci piwo…), po czym każdy chce
skonsumować ten koszyk, który jest najlepszy z dostępnych mu –
niekoniecznie ten, który przyniósł. Oczywiście im więcej
tym lepiej (przynajmniej przy ilościach, które zostały
przyniesione).
), aby łatwiej było o
intuicję, wyobraźmy sobie imprezę składkową – każdy z
jej uczestników przynosi pewien koszyk dóbr (jeden kiełbaski,
drugi chleb i musztardę, trzeci piwo…), po czym każdy chce
skonsumować ten koszyk, który jest najlepszy z dostępnych mu –
niekoniecznie ten, który przyniósł. Oczywiście im więcej
tym lepiej (przynajmniej przy ilościach, które zostały
przyniesione).
Mamy ![]() dóbr i skończony zbiór
dóbr i skończony zbiór ![]() konsumentów. Zakładamy, że każdy konsument ma zbiór możliwych decyzji
konsumentów. Zakładamy, że każdy konsument ma zbiór możliwych decyzji ![]() (gdzie
(gdzie ![]() jest pewną stałą dodatnią), a na nim
określoną funkcję użyteczności. Użyteczność
jest pewną stałą dodatnią), a na nim
określoną funkcję użyteczności. Użyteczność ![]() -tego konsumenta będziemy oznaczać przez
-tego konsumenta będziemy oznaczać przez ![]() . Standartowo będziemy zakładać, że jest ona ciągła, ściśle
quasi-wklęsła, monotoniczna i lokalnie nienasycona, jeśli
rozszerzymy ją na cały
. Standartowo będziemy zakładać, że jest ona ciągła, ściśle
quasi-wklęsła, monotoniczna i lokalnie nienasycona, jeśli
rozszerzymy ją na cały ![]() .
.
Na początku ![]() -ty konsument posiada zasób początkowy: koszyk
-ty konsument posiada zasób początkowy: koszyk ![]() . Konsumenci mogą wymieniać się dobrami, a każdy
z nich dąży do tego, żeby mieć jak najwyższą
użyteczność.
. Konsumenci mogą wymieniać się dobrami, a każdy
z nich dąży do tego, żeby mieć jak najwyższą
użyteczność.
Definicja 14.1
a) Dowolny wektor koszyków dóbr ![]() ,
taki że
,
taki że ![]() nazywamy alokacją.
nazywamy alokacją.
b) Alokację ![]() nazywamy optymalną
w sensie Pareto (lub efektywną w sensie Pareto), jeśli nie
istnieje inna alokacja
nazywamy optymalną
w sensie Pareto (lub efektywną w sensie Pareto), jeśli nie
istnieje inna alokacja ![]() , dla której
dla każdego
, dla której
dla każdego ![]() zachodzi nierówność
zachodzi nierówność ![]() i dla co najmniej jednego
i dla co najmniej jednego ![]() zachodzi
nierówność
zachodzi
nierówność ![]() .
.
c) Alokację ![]() nazywamy indywidualnie
racjonalną, jeśli dla każdego
nazywamy indywidualnie
racjonalną, jeśli dla każdego ![]() zachodzi
nierówność
zachodzi
nierówność ![]() .
.
Inaczej mówiąc, alokacja jest takim układem koszyków dóbr, który fizycznie może zostać zrealizowany, jeśli łącznie posiadamy tyle, ile wnieśli uczestnicy wymiany. Często używa się słowa podział, ale wówczas, żeby formalnie był to podział, należałoby umieścić w definicji równość zamiast nierówności. Oczywiście sensowane alokacje są podziałami: chociażby alokacje optymalne w sensie Pareto, a w szczególności równowagi (w dalszych rozważaniach).
Alokacja jest optymalna w sensie Pareto, jeśli nie jest możliwa
sytuacja, w której ”polepszamy” przynajmniej jednemu z graczy, a ”nie
pogarszamy” żadnemu innemu. Pojęcie optymalności w sensie
Pareto ma szerokie zastosowanie we wszelkich zagadnieniach optymalizacji
wielokryterialnej, w tym zagadnieniach społecznego wyboru. Pojęcie to
jest bardzo słabe – zgodnie z nim nie można porównać ze sobą alokacji, w której jeden z graczy zabiera wszystko, a drugi umiera z
głodu, z sytuacją w której bogatszy traci pewną niewielką
kwotę na rzecz biedniejszego. Ta słabość porównywania w
sensie Pareto jest jeszcze bardziej widoczna w innych zagadnieniach wyboru
społecznego – na przykład sytuacji, kiedy złodziej niszczy
transformator wart ![]() złotych, żeby ukraść drut, za
który uzyska
złotych, żeby ukraść drut, za
który uzyska ![]() złotych (a więc ”globalnie” mamy na minus
złotych (a więc ”globalnie” mamy na minus ![]() ), nie można porównać z sytaucją, kiedy do
kradzieży nie dochodzi. Tak więc gdyby stosować jedynie
kryterium Pareto, nie można by było powiedzieć, że
kradzież ze zniszczeniem jest dla społeczeństwa gorsza. Ze względu na słabość optymalności w sensie Pareto, jej brak jest
zjawiskiem bardzo negatywnym: oznacza, że marnotrawiona jest pewna
użyteczność, którą ktoś może uzyskać bez
straty użyteczności innych.
), nie można porównać z sytaucją, kiedy do
kradzieży nie dochodzi. Tak więc gdyby stosować jedynie
kryterium Pareto, nie można by było powiedzieć, że
kradzież ze zniszczeniem jest dla społeczeństwa gorsza. Ze względu na słabość optymalności w sensie Pareto, jej brak jest
zjawiskiem bardzo negatywnym: oznacza, że marnotrawiona jest pewna
użyteczność, którą ktoś może uzyskać bez
straty użyteczności innych.
Zauważmy, że jeśli wszystkie funkcje użyteczności są ściśle rosnące, to alokacje nie będące podziałami nie są optymalne w sensie Pareto – wówczas można by niewykorzystaną ilość dóbr dać przynajmniej jednemu z graczy.
Alokacja jest indywidualnie racjonalna, jeśli żaden z konsumentów nie będzie wolał swojego zasobu początkowego od proponowanego mu przy tej alokacji koszyka.
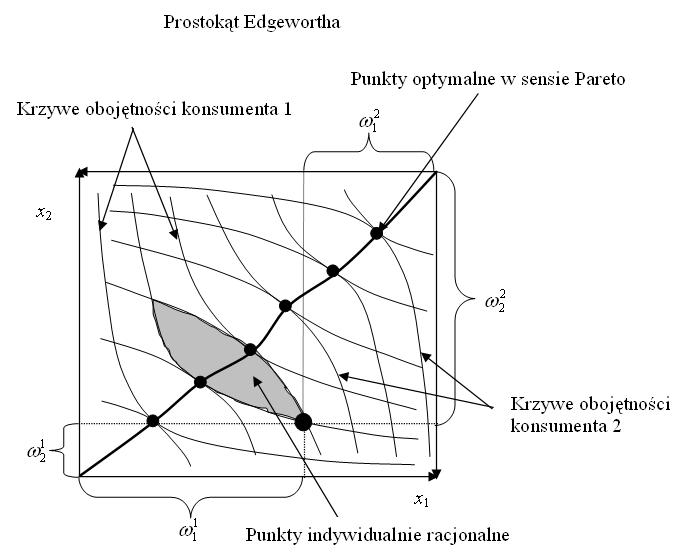
Alokacje będące podziałami przedstawia się na tak zwanym prostokącie Edgewortha (albo też pudełku Edgewortha – Edgeworth box).
Jak rysujemy prostokąt Egdewortha? Najpierw rysujemy mapę obojętności konsumenta ![]() . Następnie na tym samym rysunku umieszczamy
drugi układ współrzędnych: o początku w punkcie
. Następnie na tym samym rysunku umieszczamy
drugi układ współrzędnych: o początku w punkcie ![]() – sumie
zasobów początkowych graczy, czyli ilości dóbr, które
mamy do podziału – i obu osiach o zwrotach przeciwnych do analogicznych
osi dla konsumenta
– sumie
zasobów początkowych graczy, czyli ilości dóbr, które
mamy do podziału – i obu osiach o zwrotach przeciwnych do analogicznych
osi dla konsumenta ![]() . W drugim układzie współrzędnych rysujemy
mapę obojętności konsumenta
. W drugim układzie współrzędnych rysujemy
mapę obojętności konsumenta ![]() . Jak łatwo widać,
wszystkie punkty prostokątu Edgewortha są podziałami.
. Jak łatwo widać,
wszystkie punkty prostokątu Edgewortha są podziałami.
Optymalność w sensie Pareto i indywidualna racjonalność to minimalne właściwości, jakie powinna mieć alokacja.
Jak widać z rysunku 8.1, przeważnie jest continuum alokacji, które są równocześnie optymalne w sensie Pareto i indywidualnie racjonalne. Tak więc te dwa kryteria nie wystarczają do wyboru alokacji.
Jak więc odbywa się wymiana? Otóż na wszystkie zostają określone ceny. Te ceny nie muszą mieć jakiegokolwiek związku z rzeczywistą wartością dóbr (łyżeczka musztardy może okazać droższa niż kilo kiełbasy i butelka piwa razem wzięte), służą jedynie ustaleniu jednoznacznie alokacji równowagi. Każdy z graczy sprzedaje swój zasób początkowy i za uzyskane pieniądze kupuje taki koszyk, który maksymalizuje jego użyteczność.
Wprawdzie w odniesieniu do imprezy składkowej taki proces wydaje się nieco sztuczny, ale można na niego spojrzeć jako na konstrukcję teoretyczną pozwalającą na wybór jednej alokacji, zwłaszcza jeśli ceny nie będą w pieniądzu, ale na przykład w zapałkach albo specjalnie narysowanych imprezowych banknotach.
Definicja 14.2
Alokację ![]() wraz z wektorem cen
wraz z wektorem cen ![]() nazwiemy równowagą Walrasa dla modelu czystej wymiany towarowej,
jeśli dla każdego konsumenta jego koszyk przy alokacji jest
równy jego popytowi przy tych cenach i dochodzie równym wartości
zasobu początkowego
nazwiemy równowagą Walrasa dla modelu czystej wymiany towarowej,
jeśli dla każdego konsumenta jego koszyk przy alokacji jest
równy jego popytowi przy tych cenach i dochodzie równym wartości
zasobu początkowego ![]() oraz suma popytów jest nie większa niż suma zasobów początkowych.
oraz suma popytów jest nie większa niż suma zasobów początkowych.
Równowaga Walrasa dla modelu czystej wymiany towarowej jest więc to
taki wektor koszyków ![]() wraz z wektorem cen
wraz z wektorem cen
![]() , że
, że
1) ![]()
![]() (osiągalność przy cenach
(osiągalność przy cenach ![]() ),
),
2) ![]()
![]()
![]() (optymalność przy cenach
(optymalność przy cenach ![]() ) i
) i
3) ![]() (fizyczna dostępność).
(fizyczna dostępność).
Zauważmy, że z definicji nie widać, że równowaga musi być podziałem. Jednak jest nie tylko podziałem, jest również optymalna w sensie Pareto:
Twierdzenie 14.1
(pierwsze twierdzenie Walrasa o dobrobycie)
a) Równowaga Walrasa dla modelu czystej wymiany towarowej jest indywidualnie racjonalna.
b) Jeśli dla każdego ![]() funkcje użyteczności
funkcje użyteczności ![]() są
monotoniczne i lokalnie nienasycone, to równowaga Walrasa dla modelu
czystej wymiany towarowej jest optymalna w sensie Pareto.
są
monotoniczne i lokalnie nienasycone, to równowaga Walrasa dla modelu
czystej wymiany towarowej jest optymalna w sensie Pareto.
Tak więc choć w definicji nie zakładamy, że wszystkie dobra zostają skonsumowane, to równoważnie moglibyśmy to założyć – umieścić równość zamiast nierówności.
Weźmy alokację ![]() , która wraz z
wektorem cen
, która wraz z
wektorem cen ![]() stanowi równowagę Walrasa.
stanowi równowagę Walrasa.
a) Indywidualna racjonalność:
Przypuśćmy przeciwnie, tzn. istnieje taki konsument ![]() , że
, że ![]() . Zauważmy, że zarówno
. Zauważmy, że zarówno ![]() jak i
jak i ![]() są dostępne przy cenach
są dostępne przy cenach ![]() , a
, a ![]() maksymalizuje
maksymalizuje ![]() w zbiorze budżetowym
w zbiorze budżetowym ![]() . Tak więc
. Tak więc ![]() –
sprzeczność.
–
sprzeczność.
b) Optymalność w sensie Pareto:
Przypuśćmy przeciwnie, tzn. istnieje taka alokacja ![]() fizycznie dostępna, że dla każdego
konsumenta
fizycznie dostępna, że dla każdego
konsumenta ![]()
![]() i istnieje
i istnieje ![]() , że
, że ![]() . Ponieważ to
. Ponieważ to ![]() a nie
a nie ![]() został
wybrany,
został
wybrany, ![]() nie mogło być dostępne przy cenach, czyli
nie mogło być dostępne przy cenach, czyli ![]() . Ponieważ funkcja
. Ponieważ funkcja ![]() jest monotoniczna i lokalnie nienasycona, więc spełnia prawo Walrasa.
Tak więc dla każdego
jest monotoniczna i lokalnie nienasycona, więc spełnia prawo Walrasa.
Tak więc dla każdego ![]()
![]() nie może należeć do wnętrza
nie może należeć do wnętrza ![]() , czyli
, czyli ![]() (z przynajmniej jedną
nierównością ostrą, co przed chwilą pokazaliśmy).
(z przynajmniej jedną
nierównością ostrą, co przed chwilą pokazaliśmy).
Jeżeli zsumujemy te wszystkie nierówności po ![]() , otrzymamy
, otrzymamy ![]() .
.
Natomiast gdy przemożymy nierówność fizycznej dostępności obustronnie przez ![]() , otrzymamy
, otrzymamy ![]() – sprzeczność.
– sprzeczność.
Kolejnym pytaniem jest, czy dowolny koszyk optymalny w sensie Pareto i indywidualnie racjonalny można uzyskać dobierając odpowiednie ceny. I tu odpowiedź jest również twierdząca.
Twierdzenie 14.2
(drugie twierdzenie Walrasa o dobrobycie)
Przy założeniach modelu jeśli alokacja ![]() jest optymalna w sensie Pareto, to istnieje taki układ zasobów początkowych konsumentów
jest optymalna w sensie Pareto, to istnieje taki układ zasobów początkowych konsumentów ![]() oraz wektor cen
oraz wektor cen ![]() , że
, że ![]() z
z ![]() stanowi
równowagę Walrasa dla modelu czystej wymiany towarowej przy układzie zasobów początkowych konsumentów
stanowi
równowagę Walrasa dla modelu czystej wymiany towarowej przy układzie zasobów początkowych konsumentów ![]() .
.
Dla dwóch konsumentów – wszystko to będziemy rozważać
na prostokącie Edgewortha, gdzie zbiory związane z ![]() -tym
konsumentem zaznaczamy w jego układzie współrzędnych. Będziemy korzystać z twierdzenia o hiperpłaszczyźnie rozdzielającej. Ponieważ
-tym
konsumentem zaznaczamy w jego układzie współrzędnych. Będziemy korzystać z twierdzenia o hiperpłaszczyźnie rozdzielającej. Ponieważ ![]() – optymalny w sensie
Pareto, więc stanowi on ”punkt styczności” dwóch zbiorów
– optymalny w sensie
Pareto, więc stanowi on ”punkt styczności” dwóch zbiorów ![]() w prostokącie
Edgewortha – należy do brzegu obu. Ponieważ
w prostokącie
Edgewortha – należy do brzegu obu. Ponieważ ![]() – quasi-wklęsłe, te zbiory są wypukłe. Rozdzielamy wnętrza tych zbiorów
– dwa zbiory wypukłe rozłączne. Z jednego z twierdzeń o
hiperpłaszczyźnie rozdzielającej dwa zbiory wypukłe rozłączne
– quasi-wklęsłe, te zbiory są wypukłe. Rozdzielamy wnętrza tych zbiorów
– dwa zbiory wypukłe rozłączne. Z jednego z twierdzeń o
hiperpłaszczyźnie rozdzielającej dwa zbiory wypukłe rozłączne ![]() i
i ![]() istnieje wektor
istnieje wektor ![]() ,
że dla każdego
,
że dla każdego ![]() i
i ![]()
![]() . W naszym przypadku
. W naszym przypadku ![]() i
i ![]() to zbiory
to zbiory ![]() dla obu graczy w prostokącie
Edgewortha. Ten wektor
dla obu graczy w prostokącie
Edgewortha. Ten wektor ![]() ma wszystkie współrzędne
nieujemne, gdyż
ma wszystkie współrzędne
nieujemne, gdyż ![]() zawiera
zawiera ![]() , tak więc jest naszym
wektorem cen równowagi przy dowolnym
, tak więc jest naszym
wektorem cen równowagi przy dowolnym ![]() należącego do prostej rozdzielającej.
należącego do prostej rozdzielającej.
Kolejne naturalne pytanie, to czy równowaga istnieje. Odpowiedź jest również twierdząca, lecz odpowiednie twierdzenie sformułujemy dla znacznie ogólniejszego modelu – modelu Arrowa-Debreu, w którym oprócz konsumentów mamy również producentów.
Ćwiczenie 14.1
Na bezludnej wyspie mieszkają tylko Robinson i Piętaszek. Robinson ma 10 orzechów kokosowych i dwie ryby, a Piętaszek 5 ryb i jeden orzech. Ich funkcje użyteczności to, odpowiednio ![]() i
i ![]() .
Naszkicować prostokąt Edgewortha i zaznaczyć na nim podziały indywidualnie racjonalne i podziały optymalne w sensie Pareto.
Obliczyć równowagę Walrasa jeśli jest lub udowodnić, że jej nie ma.
.
Naszkicować prostokąt Edgewortha i zaznaczyć na nim podziały indywidualnie racjonalne i podziały optymalne w sensie Pareto.
Obliczyć równowagę Walrasa jeśli jest lub udowodnić, że jej nie ma.
Ćwiczenie 14.2
Bliźniaczki Joasia i Kasia dostały w prezencie od szalonego wujka buty – jednakowe poza jedną cechą: Joasia dostała 3 buty prawe, a Kasia 4 lewe.
Preferencje dziewczynek co do butów są naturalne – im więcej par, tym lepiej.
Czy w modelu istnieje równowaga Walrasa? Jeśli tak, obliczyć.
14.2. Model Arrowa-Debreu
Założenia o konsumentach w modelu Arrowa-Debreu są takie same jak w modelu czystej wymiany towarowej.
Ponadto mamy skończony zbiór ![]() firm.
firm.
Każdy konsument może posiadać akcje firm. Liczbę akcji ![]() -tej firmy w rękach
-tej firmy w rękach ![]() -tego konsumenta będziemy oznaczać przez
-tego konsumenta będziemy oznaczać przez ![]() . Akcja oznacza udział w zysku (czyli także udział w
stracie, jeśli firma przynosi stratę). Tak więc zakładamy,
że
. Akcja oznacza udział w zysku (czyli także udział w
stracie, jeśli firma przynosi stratę). Tak więc zakładamy,
że ![]() .
.
Firma ![]() ma zbiór dostępnych technologii
ma zbiór dostępnych technologii ![]() . Wszystkie
. Wszystkie ![]() są niepuste, domknięte i
ściśle wypukłe. Każda z firm maksymalizuje zysk, traktując
ceny jako dane, przy czym kupuje czynniki produkcji od konsumentów i
sprzedaje im produkty.
są niepuste, domknięte i
ściśle wypukłe. Każda z firm maksymalizuje zysk, traktując
ceny jako dane, przy czym kupuje czynniki produkcji od konsumentów i
sprzedaje im produkty.
Definicja 14.3
Równowagą Walrasa nazywamy układ wektorów ![]() ,
, ![]() wraz z wektorem cen
wraz z wektorem cen ![]() , taki że
, taki że
1) ![]()
![]() (wykonalność
planów produkcyjnych);
(wykonalność
planów produkcyjnych);
2) ![]()
![]() (osiągalność planów konsumpcyjnych przy cenach
(osiągalność planów konsumpcyjnych przy cenach ![]() );
);
3) ![]()
![]()
![]() (maksymalizacja zysku przez
producentów);
(maksymalizacja zysku przez
producentów);
4) ![]()
![]()
![]() (maksymalizacja użyteczności
przez konsumentów);
(maksymalizacja użyteczności
przez konsumentów);
5) ![]() (fizyczna dostępność planów konsumpcyjnych), przy czym
jeśli po
(fizyczna dostępność planów konsumpcyjnych), przy czym
jeśli po ![]() -tej współrzędnej nierówność jest
ostra, to
-tej współrzędnej nierówność jest
ostra, to ![]() .
.
Twierdzenie 14.3
Przy założeniach modelu istnieje równowaga Walrasa.
Niech ![]() oznacza plan produkcyjny maksymalizujący zysk
producenta
oznacza plan produkcyjny maksymalizujący zysk
producenta ![]() przy cenie
przy cenie ![]() , a
, a ![]() – koszyk
maksymalizujący użyteczność konsumenta
– koszyk
maksymalizujący użyteczność konsumenta ![]() wśród osiągalnych przy
wśród osiągalnych przy ![]() planów konsumpcyjnych, przy założeniu że producenci wybierają swoje
planów konsumpcyjnych, przy założeniu że producenci wybierają swoje ![]() .
.
Z twierdzenia o maksimum ![]() jest ciągłą funkcją zmiennej
jest ciągłą funkcją zmiennej ![]() . Z powyższego faktu i z twierdzenia o maksimum,
również
. Z powyższego faktu i z twierdzenia o maksimum,
również ![]() jest ciągłą funkcją zmiennej
jest ciągłą funkcją zmiennej ![]() .
.
Konstruujemy funkcję nadwyżki popytu ![]() (ujemne wartości oznaczają nadwyżkę podaży).
(ujemne wartości oznaczają nadwyżkę podaży).
Z prawa Walrasa dla optymalizacji konsumenta otrzymujemy, że dla
każdego ![]()
![]() .
.
Twierdzenie 14.4 (Prawo Walrasa (dla rynku))
Przy założeniach modelu dla każdego wektora cen ![]()
![]() (nadwyżka popytu jest prostopadła do
(nadwyżka popytu jest prostopadła do ![]() ).
).
Ekonomiści formułują to jako ”wartość niedoborów jest równa wartości nadwyżek”.
(prawa Walrasa dla rynku)
Jeśli dodamy równości wynikające z prawa Walrasa dla
konsumentów, otrzymamy
![]()
![]() (ponieważ udziały sumują się do
(ponieważ udziały sumują się do ![]() )
)
![]()
![]() .
.
Wracamy do dowodu twierdzenia o istnieniu równowagi.
Twierdzenie to można równoważnie sformułować: istnieje
cena, dla której nadwyżka popytu jest równa ![]() . Ponieważ na
pewno nie jest to wektor
. Ponieważ na
pewno nie jest to wektor ![]() , a zarówno
, a zarówno ![]() jak i
jak i ![]() są jednorodne stopnia
są jednorodne stopnia ![]() , możemy ograniczyć się do
wektorów cen, których współrzędne sumują się do
, możemy ograniczyć się do
wektorów cen, których współrzędne sumują się do ![]() – sympleksu
– sympleksu ![]() .
.
Ustalam dowolny wektor cen ![]() . Przy tych cenach mogą wystąpić niedobory – w konstrukcji nowej ceny
. Przy tych cenach mogą wystąpić niedobory – w konstrukcji nowej ceny ![]() rozpatrywać tylko faktyczne nadwyżki, zaniedbując niedobory.
Wprowadzamy oznaczenie: dla
rozpatrywać tylko faktyczne nadwyżki, zaniedbując niedobory.
Wprowadzamy oznaczenie: dla ![]() oznaczmy przez
oznaczmy przez ![]() wektor
wektor ![]() .
.
Na sympleksie ![]() definiujemy funkcję
definiujemy funkcję ![]() .
.
Funkcja ![]() i jest ciągła, a więc na
mocy twierdzenia Brouwera istnieje
i jest ciągła, a więc na
mocy twierdzenia Brouwera istnieje ![]() takie, że
takie, że ![]() .
.
Czyli dla każdego ![]()
![]() .
Stąd
.
Stąd ![]() ,
czyli
,
czyli ![]() ,
,
![]()
![]() , co
sumujemy po
, co
sumujemy po ![]() i otrzymujemy:
i otrzymujemy:
![]() , a więc
, a więc
![]() Z prawa Walrasa dla rynku
Z prawa Walrasa dla rynku ![]() , a więc
, a więc
![]() , czyli nie ma faktycznych nadwyżek popytu– mogą być tylko
niedobory. Tak więc
, czyli nie ma faktycznych nadwyżek popytu– mogą być tylko
niedobory. Tak więc ![]() – brakujący warunek 5. równowagi Walrasa
(reszta była automatycznie spełniona).
– brakujący warunek 5. równowagi Walrasa
(reszta była automatycznie spełniona).
Twierdzenie o istnieniu udowodniliśmy przy bardzo silnych założeniach. Gdybyśmy nie zakładali ścisłej a tylko zwykłą quasi-wklęsłość funkcji użyteczności lub wypukłość zbiorów dostępnych technologii, nie ma wówczas jednoznaczności – popyt lub podaż nie jest funkcją, lecz odwzorowaniem wielowartościowym. Twierdzenie o istnieniu równowagi Walrasa pozostaje prawdziwe, lecz dowód staje się bardziej skomplikowany, jednak wszystko się przenosi: zamiast funkcji popytu i podaży mamy odwzorowania wielowartościowe, zamiast ciągłości funkcji – półciągłość górną odzworowań wielowartościowych, a twierdzenie Brouwera trzeba zastąpić twierdzeniem Kakutaniego o istnieniu punktu stałego dla odwzorowania wielowartościowego.