Zagadnienia
3. Narzędzia
3.1. Optymalizacja
Aby analizować zagadnienia teorii wyboru, potrzebujemy trochę teorii optymalizacji. Niektóre z poniższych faktów są zapewne państwu znane.
Zaczniemy od warunku koniecznego optymalności (tzw. warunku pierwszego rzędu).
Twierdzenie 3.1
(mnożniki Lagrange'a)
Niech ![]() i niech funkcje
i niech funkcje ![]() i
i
![]() dla
dla ![]() będą
różniczkowalne. Jeżeli w punkcie
będą
różniczkowalne. Jeżeli w punkcie ![]() , jest
przyjmowane maximum (minimum)
, jest
przyjmowane maximum (minimum) ![]() na zbiorze
na zbiorze ![]() dla
dla ![]() i gradienty funkcji
i gradienty funkcji ![]() są liniowo niezależne w
są liniowo niezależne w
![]() , to istnieje taki wektor
, to istnieje taki wektor ![]() , że
, że ![]() .
.
Definicja 3.1
Funkcję ![]() nazywamy lagrangianem, a wektor
nazywamy lagrangianem, a wektor ![]() nazywamy mnożnikami Lagrange'a.
nazywamy mnożnikami Lagrange'a.
Twierdzenie można sformułować następująco: punkt optymalny
dla optymalizacji z ograniczeniami równościowymi wraz wektorem
mnożników musi być punktem krytycznym lagrangianu (zerowanie
pochodnej po ![]() to równości definiujące zbiór
dopuszczalny).
to równości definiujące zbiór
dopuszczalny).
Uwaga: Dla uproszczenia zapisu wyników maksymalizacji
(minimalizacji) funkcji ![]() po zbiorze
po zbiorze ![]() , wprowadzimy symbole
, wprowadzimy symbole ![]() (
(![]() ) na
zbiór tych punktów, w których maksimum (minimum) jest
przyjmowane.
) na
zbiór tych punktów, w których maksimum (minimum) jest
przyjmowane.
Ponadto, jeżeli maksymalizujemy funkcję po pewnym zbiorze i ten
zbiór okaże się pusty, wówczas za maksimum przyjmujemy ![]() (analogicznie za minimum
(analogicznie za minimum ![]() ).
).
Przykład 3.1
Znajdowanie maksimum ściśle monotonicznej,
ściśle wklęsłej i różniczkowalnej funkcji
użyteczności ![]() na Walrasowskim zbiorze budżetowym
na Walrasowskim zbiorze budżetowym ![]() (gdzie
(gdzie ![]() ) przy pomocy
mnożników Lagrange'a.
) przy pomocy
mnożników Lagrange'a.
W niniejszym przykładzie rozwiązujemy zagadnienie, z jakim mamy do
czynienia zazwyczaj przy wyborze konsumenta: funkcja użyteczności
jest ściśle monotoniczna, i wklęsła, a zbiory budżetowe są walrasowskie. Ponieważ ![]() jest monotoniczna, więc
jest monotoniczna, więc ![]() . Ponieważ ponadto
. Ponieważ ponadto ![]() jest ściśle monotoniczna, także
jest ściśle monotoniczna, także ![]() , co sprowadza optymalizację z
ograniczeniem nierównościowym do optymalizacji z ograniczeniem
równościowym.
, co sprowadza optymalizację z
ograniczeniem nierównościowym do optymalizacji z ograniczeniem
równościowym.
Lagrangian zagadnienia ma postać ![]() , a więc warunki konieczne na to, aby w
punkcie
, a więc warunki konieczne na to, aby w
punkcie ![]() o obu współrzędnych dodatnich było przyjmowane
maksimum to:
o obu współrzędnych dodatnich było przyjmowane
maksimum to:
![]() ,
,
![]() ,
,
![]() .
.
Przeanalizujmy dwa pierwsze równania:
![]() ,
,
![]() .
.
Ponieważ ![]() jest ściśle monotoniczna, w
jest ściśle monotoniczna, w ![]() nie może
być przyjmowane maksimum globalne
nie może
być przyjmowane maksimum globalne ![]() , a ponieważ funkcja jest
ściśle wklęsła, pochodna może się zerować tylko w
maksimum globalnym, stąd wiemy, że
, a ponieważ funkcja jest
ściśle wklęsła, pochodna może się zerować tylko w
maksimum globalnym, stąd wiemy, że ![]() . Możemy więc podzielić równania przez siebie stronami. Otrzymamy
. Możemy więc podzielić równania przez siebie stronami. Otrzymamy 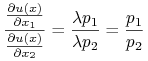 .
.
Jest to warunek konieczny maksymalizacji w naszym przypadku. Ma on
interpretacje zarówno ekonomiczną jak i graficzną. Obie będą bardziej oczywiste, jeżeli powyższe równanie pomnożymy
przez ![]() :
:
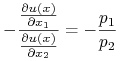 .
.
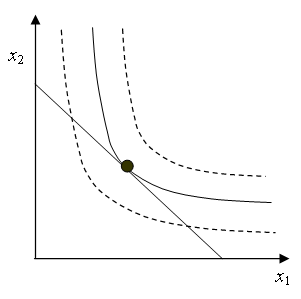
Prawa strona to oczywiście nachylenie ograniczenia budżetowego,
natomiast lewa to nachylenie krzywej obojętności przechodzącej
przez punkt ![]() (co łatwo wynika z twierdzenia o funkcji uwikłanej), a więc to, co otrzymaliśmy, to warunek konieczny styczności:
równość nachyleń w punkcie styczności.
(co łatwo wynika z twierdzenia o funkcji uwikłanej), a więc to, co otrzymaliśmy, to warunek konieczny styczności:
równość nachyleń w punkcie styczności.
Interpretacja ekonomiczna brzmi: krańcowa stopa substytucji równa się, co do modułu, stosunkowi cen.
Definicja 3.2
Krańcową stopą substytucji pomiędzy dobrami ![]() i
i ![]() w punkcie
w punkcie ![]() nazywamy współczynnik kierunkowy krzywej obojętności w punkcie
nazywamy współczynnik kierunkowy krzywej obojętności w punkcie ![]() . Oznaczamy ją skrótem
. Oznaczamy ją skrótem ![]() (od angielskiego marginal rate of substitution).
(od angielskiego marginal rate of substitution).
Z twierdzenia o funkcji uwikłanej mamy więc 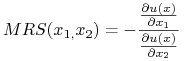 .
.
Uwaga 3.1
W niektórych podręcznikach krańcowa stopa substytucji jest definiowana bez minusa, a czasem nawet zdarzają się niekonsekwencje: jest definiowana jako nachylenie, a więc z minusem, a potem minus ginie w stwierdzeniu ”krańcowa stopa substytucji równa się stosunkowi cen” i tym podobnych.
Uwaga 3.2
Interpetacja łopatologiczna słowa ”krańcowy”, czyli pochodnych w ekonomii, jako skutku zmiany o jednostkę. W przypadku teorii wyboru konsumenta ma to niewielki sens, natomiast w przypadku wyboru producenta, przy bardzo dużych nakładach produkcji może być w miarę przyzwoitym przybliżeniem.
A więc ekonomista może zdefiniować krańcową stopę
substytucji słowami: ”o ile musi zmienić się konsumpcja dobra ![]() jesłi konsumpcja dobra
jesłi konsumpcja dobra ![]() zwiększyła się o jednostkę,
abyśmy pozostali na tej samej krzywej obojętności”.
zwiększyła się o jednostkę,
abyśmy pozostali na tej samej krzywej obojętności”.
Warunek dostateczny optymalności uogólnia warunek dostateczny dla
przypadku optymalizacji bez ograniczeń: jeśli w dopuszczalnym ![]() spełniony jest warunek pierwszego rzędu i macierz drugiej pochodnej
jest dodatnio określona w dowolnym kierunku dopuszczalnym (tzn.
spełniony jest warunek pierwszego rzędu i macierz drugiej pochodnej
jest dodatnio określona w dowolnym kierunku dopuszczalnym (tzn. ![]() dla
dla ![]() takich, że
takich, że ![]() ), to w punkcie
), to w punkcie ![]() jest przyjmowane minimum,
jeśli natomiast ujemnie określona – maksimum. Ponieważ jednak
badanie określoności macierzy dla wektorów z pewnej
podprzestrzeni nie jest trywialne, sformułujemy ten warunek
równoważnie.
jest przyjmowane minimum,
jeśli natomiast ujemnie określona – maksimum. Ponieważ jednak
badanie określoności macierzy dla wektorów z pewnej
podprzestrzeni nie jest trywialne, sformułujemy ten warunek
równoważnie.
Twierdzenie 3.2
Niech ![]() . Jeśli w dopuszczalnym punkcie
. Jeśli w dopuszczalnym punkcie ![]() spełnione są
warunki pierwszego rzędu dla pewnego mnożnika
spełnione są
warunki pierwszego rzędu dla pewnego mnożnika ![]() i
jeśli dla
i
jeśli dla ![]() minory główne
minory główne ![]() macierzy
macierzy ![]() spełniają warunek
spełniają warunek ![]() , to w
, to w ![]() jest przyjmowane minimum, jeśli natomiast
jest przyjmowane minimum, jeśli natomiast ![]() , to maksimum.
, to maksimum.
Twierdzenie 3.3
Jeśli funkcja ![]() jest wklęsła,
jest wklęsła, ![]() liniowa i
liniowa i ![]() dopuszczalny
spełnia warunek pierwszego rzędu, to w
dopuszczalny
spełnia warunek pierwszego rzędu, to w ![]() jest przyjmowane
maksimum, a jeśli
jest przyjmowane
maksimum, a jeśli ![]() jest wypukła, to minimum.
jest wypukła, to minimum.
W przypadku ograniczeń nierównościowych mamy podobne warunki pierwszego rzędu.
Twierdzenie 3.4
(warunki konieczne Kuhna-Tuckera albo Karusha-Kuhna-Tuckera)
Niech ![]() i niech funkcje
i niech funkcje ![]() i
i
![]() będą różniczkowalne. Jeżeli w punkcie
będą różniczkowalne. Jeżeli w punkcie ![]() , jest przyjmowane
maximum
, jest przyjmowane
maximum ![]() na zbiorze
na zbiorze ![]() dla
dla ![]() ;
; ![]() dla
dla ![]() i gradienty w
i gradienty w ![]() funkcji
funkcji ![]() oraz tych z
funkcji
oraz tych z
funkcji ![]() , dla których
, dla których ![]() , są liniowo
niezależne, to istnieją takie wektory
, są liniowo
niezależne, to istnieją takie wektory ![]() ,
,
![]() że
że ![]() . Ponadto jeśli
. Ponadto jeśli ![]() ,
to
,
to ![]() .
.
Ćwiczenie 3.1
Powtórzyć analizę przykładu 3.1 bez założenia ścisłej dodatniości współrzędnych przy użyciu warunków koniecznych Kuhna-Tuckera.
Warunków koniecznych Kuhna-Tuckera można użyć nawet do rozwiązania zagadnień maksymalizacjnych, do których zazwyczaj nie przyszłoby nam do głowy liczenie pochodnej – maksymalizacji funkcji liniowej przy ograniczeniach liniowych.
Ćwiczenie 3.2
Rozwiązać zagadnienie maksymalizacji ![]() (doskonałe substytuty) na Walrasowskim zbiorze budżetowym w
(doskonałe substytuty) na Walrasowskim zbiorze budżetowym w ![]() .
.
W przypadku ograniczeń nierównościowych wektor mnożników
(tzw. mnożników Kuhna-Tuckera) jest nieujemny, istotny jest więc
kierunek nierówności. Dlatego, aby uzyskać nieujemny wektor
mnożników w przypadku zagadnienia minimalizacji, musimy zapisać
ograniczenia w postaci ![]() . Musimy na to też
zwrócić uwagę przy warunkach drugiego rzędu.
. Musimy na to też
zwrócić uwagę przy warunkach drugiego rzędu.
Twierdzenie 3.5
Jeśli ![]() dopuszczalny spełnia warunek pierwszego rzędu, a
funkcja
dopuszczalny spełnia warunek pierwszego rzędu, a
funkcja ![]() jest wklęsła, funkcje
jest wklęsła, funkcje ![]() wypukłe,
wypukłe, ![]() liniowe,
to w
liniowe,
to w ![]() jest przyjmowane maksimum
jest przyjmowane maksimum ![]() na zbiorze
na zbiorze ![]() dla
dla ![]() ;
; ![]() dla
dla ![]() , a jeśli
, a jeśli ![]() jest wypukła a funkcje
jest wypukła a funkcje ![]() wklęsłe,
wklęsłe, ![]() liniowe, to minimum
liniowe, to minimum ![]() na zbiorze
na zbiorze ![]() dla
dla ![]() , ;
, ; ![]() dla
dla ![]() .
.
Definicja 3.3
Funkcję ![]() nazywamy górnie (dolnie) półciągła, jeśli dla każdego
nazywamy górnie (dolnie) półciągła, jeśli dla każdego ![]() i
i ![]() istnieje
istnieje ![]() , taka że dla
, taka że dla ![]() dla
których
dla
których ![]() zachodzi własność
zachodzi własność ![]() (dla dolnej półciągłości
(dla dolnej półciągłości ![]() ).
).
Definicja 3.4
a) Funkcję ![]() nazywamy quasi-wklęsłą, jeśli dla każdego
nazywamy quasi-wklęsłą, jeśli dla każdego ![]() i dla każdego
i dla każdego ![]() zachodzi warunek
zachodzi warunek ![]() .
.
b) Funkcja ![]() jest ściśle quasi-wklęsła, jeśli dla
każdego
jest ściśle quasi-wklęsła, jeśli dla
każdego ![]() i dla każdego
i dla każdego ![]() zachodzi warunek
zachodzi warunek ![]() .
.
c) Funkcja ![]() jest quasi-wypukła (ściśle),
jeśli funkcja
jest quasi-wypukła (ściśle),
jeśli funkcja ![]() jest quasi wklęsła (ściśle).
jest quasi wklęsła (ściśle).
Każda funkcja wklęsła jest quasi wklęsła, natomiast nie na
odwrót. W szczególności funkcja quasi wklęsła nie musi
być ciągła, a funkcja wklęsła określona na zbiorze
otwartym jest ciągła. Funkcją quasi-wklęsłą może
być nawet funkcja ściśle wypukła określona na odcinku, o
ile nie ma minimum w jego wnętrzu: na przykład ![]() .
.
Stwierdzenie 3.1
a) Funkcja ![]() jest quasi wklęsła wtedy i tylko wtedy, gdy
jest quasi wklęsła wtedy i tylko wtedy, gdy ![]()
![]() jest wypukły;
jest wypukły;
b) Funkcja ![]() jest ściśle quasi wklęsła wtedy i tylko wtedy,
gdy
jest ściśle quasi wklęsła wtedy i tylko wtedy,
gdy ![]()
![]() jest wypukły i
jest wypukły i ![]() jeśli
jeśli ![]() , to
, to ![]()
![]() .
.
Na mocy tego stwierdzenia możemy coś powiedzieć na temat funkcji użyteczności odzwierciedlającej wypukłe preferencje.
Stwierdzenie 3.2
Każda funkcja użyteczności odzwierciedlająca wypukłe preferencje jest quasi wklęsła, a ściśle wypukłe – ściśle quasi wklęsła.
Twierdzenie 3.6
(istnienie i jednoznaczność maximum)
a) Jeżeli funkcja ![]() jest górnie
półciągła a zbiór
jest górnie
półciągła a zbiór ![]() niepusty, zwarty, to istnieje punkt
realizujący maksimum
niepusty, zwarty, to istnieje punkt
realizujący maksimum ![]() na
na ![]() .
.
b) Jeżeli funkcja ![]() jest ściśle
quasi-wklęsła a zbiór
jest ściśle
quasi-wklęsła a zbiór ![]() wypukły, to istnieje co najwyżej
jeden punkt realizujący maksimum
wypukły, to istnieje co najwyżej
jeden punkt realizujący maksimum ![]() na
na ![]() .
.
c) Jeżeli funkcja ![]() jest quasi-wklęsła a zbiór
jest quasi-wklęsła a zbiór ![]() wypukły, to zbiór punktów realizujących
maksimum
wypukły, to zbiór punktów realizujących
maksimum ![]() na
na ![]() jest wypukły.
jest wypukły.
Twierdzenie 3.7
(twierdzenie o obwiedni dla maksymalizacji z ograniczeniami)
a) Niech ![]() i niech funkcje
i niech funkcje ![]() i
i ![]() będą
różniczkowalne i takie, że dla każdego
będą
różniczkowalne i takie, że dla każdego ![]() ,
,![]()
![]() jest przyjmowane w dokładnie jednym punkcie
jest przyjmowane w dokładnie jednym punkcie ![]() dla jednoznacznego wektora mnożników
dla jednoznacznego wektora mnożników ![]() i tak zdefiniowana
funkcja
i tak zdefiniowana
funkcja ![]() jest różniczkowalna. Definiujemy
jest różniczkowalna. Definiujemy ![]() . Dla funkcji
. Dla funkcji ![]() zachodzi następująca własność:
zachodzi następująca własność:
![]() .
.
b) Niech ![]() i niech funkcje
i niech funkcje ![]() i
i ![]() będą
różniczkowalne i takie, że dla każdego
będą
różniczkowalne i takie, że dla każdego ![]() ,
,![]()
![]() jest przyjmowane w dokładnie jednym punkcie
jest przyjmowane w dokładnie jednym punkcie ![]() dla jednoznacznego wektora mnożników
dla jednoznacznego wektora mnożników ![]() i tak
zdefiniowane funkcje
i tak
zdefiniowane funkcje ![]() i
i ![]() są różniczkowalne.
Definiujemy
są różniczkowalne.
Definiujemy ![]() . Dla funkcji
. Dla funkcji ![]() zachodzi następująca własność:
zachodzi następująca własność:
![]() .
.
Wniosek 3.1
(twierdzenie o obwiedni dla maksymalizacji bez ograniczeń)
Niech ![]() i niech funkcja
i niech funkcja ![]() będzie różniczkowalna i taka, że dla
każdego
będzie różniczkowalna i taka, że dla
każdego ![]() ,
,![]()
![]() jest przyjmowane w
dokładnie jednym punkcie
jest przyjmowane w
dokładnie jednym punkcie ![]() i tak zdefiniowana funkcja
i tak zdefiniowana funkcja ![]() jest
różniczkowalna. Definiujemy
jest
różniczkowalna. Definiujemy ![]() . Dla
funkcji
. Dla
funkcji ![]() zachodzi następująca własność:
zachodzi następująca własność: ![]() .
.
Ćwiczenie 3.3
Udowodnić twierdzenia o obwiedni.
Definicja 3.5
Niech ![]() i funkcja
i funkcja ![]() . Funkcję
. Funkcję ![]() nazywamy (dodatnio) jednorodną stopnia
nazywamy (dodatnio) jednorodną stopnia ![]() , jeżeli dla
każdego
, jeżeli dla
każdego ![]() ,
, ![]() mamy
mamy ![]() .
.