Zagadnienia

7.1 Klasyfikacje dóbr
7.2 Własności funkcji popytu

7. Teoria wyboru konsumenta – funkcje popytu i ich własności

7.1. Klasyfikacje dóbr

W niniejszym rozdziale skoncentrujemy się na samych odwzorowaniach popytu. Będziemy badać, jak się zmienia zachowanie konsumenta, kiedy zmieniają się warunki wyboru.

To, co mamy przeważnie dane z badań rynku, to pewna selekcja z odwzorowania $x$ . Odtąd będziemy zakładać, że jest to jedyna możliwa selekcja z $x$ , czyli że odzworowanie popytu $x$ jest funkcją. W dalszych rozważaniach będziemy ponadto zakładać, że jest to funkcja różniczkowalna.

Ponieważ $x$ jest funkcją wielu zmiennych, aby badać interesujące nas efekty, będziemy często ustalać część zmiennych i przy tym założeniu badać własności funkcji popytu jako funkcję wyróżnionych zmiennych. Ponieważ te obiekty badano już, zanim pojawiła się formalna teoria wyboru, mają swoje nazwy:

Definicja 7.1

Przy ustalonym wektorze cen $\mathbf{p}$ funkcję $x(\mathbf{p},\cdot)$ nazywamy ścieżką ekspansji dochodu, natomiast funkcje $x_{{i}}(\mathbf{p},\cdot)$ – krzywymi Engla (Engel curves).

Przy ustalonych cenach $p_{{j}}$ dla $j\neq i$ i dochodzie $m$ , funkcje $x_{{i}}(p_{{1}},\ldots,p_{{i-1}},\cdot,p_{{i+1}},\ldots,p_{{n}},m)$ nazywamy krzywymi oferty cenowej.

Będziemy badać, jak reagują funkcje popytu na zmianę tylko jednego parametru.

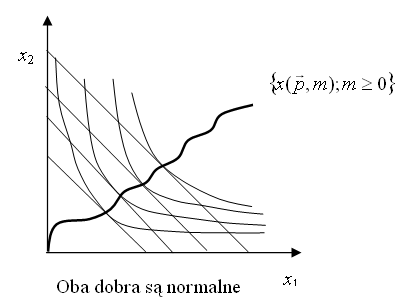
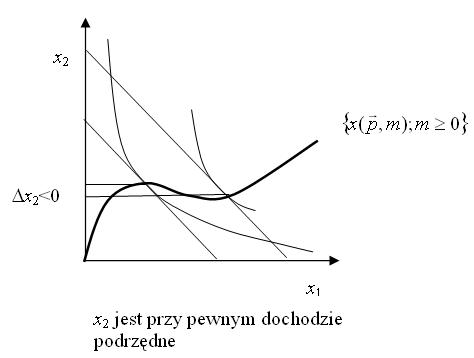
Zaczniemy od zbadania, jak zmienia się popyt w zależności od dochodu. Zazwyczaj naturalnym założeniem jest, że im większy mamy dochód, tym więcej danego typu dóbr konsumujemy (jest to sytuacja normalna, stąd poniższe określenie). Jednak nie zawsze musi tak być.

Definicja 7.2

Dobro $i$ nazywamy normalnym przy cenach $\mathbf{p}$ i dochodzie $\bar{m}$ , jeśli $\frac{\partial x_{{i}}(\mathbf{p},\bar{m})}{\partial m}>0$ . Jeśli $\frac{\partial x_{{i}}(\mathbf{p},\bar{m})}{\partial m}<0$ , to dobro $i$ jest podrzędne (niższego rzędu, poślednie) przy cenach $\mathbf{p}$ i dochodzie $\bar{m}$ . Dobro $i$ jest normalne, jeśli jest normalne przy każdych cenach i poziomie dochodu.

Można też definiować normalność/podrzędność $i$ w konkretnym punkcie jako warunek, że $x_{{i}}$ jest jest rosnąca/malejąca jako funkcja $m$ w pewnym otoczeniu $\bar{m}$ (i, w zasadzie, to jest to, o co nam naprawdę chodzi). Takie pojęcia normalności/podrzędności nie są równoważne powyższej definicji nawet dla funkcji różniczkowalnych, ale na pewno wynikają z niego.

Rys. 7.1. Dwa dobra normalne.

Rys. 7.2. Dobro podrzędne – $x_{2}$ .

Ćwiczenie 7.1

Czy jest możliwe, by:

a) dobro $i$ było podrzędne przy ustalonym wektorze cen dla wszystkich poziomów dochodu?

b) wszystkie dobra konsumowane przez konsumenta były normalne?

c) wszystkie dobra konsumowane przez konsumenta były podrzędne?

Przykładem dóbr podrzędnych są wszelkie produkty niskiej jakości, dla których istnieją ”odpowiedniki” lepszej jakości: np. mortadela, obuwie ze Stadionu Dziesięciolecia.

Jeżeli natomiast jako dobro rozważamy całą klasę dóbr np. żywność czy odzież, to na pewno mamy do czynienia z dobrem normalnym.

Ćwiczenie 7.2

Pokazać, że przy odpowiednich założeniach o regularności funkcji i odwzorowań modelu konsumenta, dobro $i$ jest normalne wtedy i tylko wtedy, gdy $\frac{\partial^{2}e(\mathbf{p},\bar{u})}{\partial p_{i}\partial\bar{u}}>0$ .

Wskazówka:

Skorzystać z lematu Shepharda i dualności.

Jeśli już ustaliliśmy, że mamy do czynienia z dobrem normalnym, pojawia się kolejne pytanie: jak szybko rośnie popyt – wolniej czy szybciej niż dochód. Aby móc analizować tego typu zależności, potrzebne będzie nam nowe pojęcie: elastyczność. Zaczniemy od ogólnej definicji elastyczności jednej wielkości względem drugiej.

Definicja 7.3

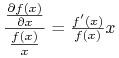Jeżeli rozważamy zależność pomiędzy rzeczywistymi wielkościami $x$ i $y$ określoną funkcją $f(x)=y$ , to elastycznością $y$ względem $x$ nazywamy wielkość $\dfrac{\frac{\partial f(x)}{\partial x}}{\frac{f(x)}{x}}=\frac{f^{{\prime}}(x)}{f(x)}x$ .

Ekonomiści interpretują tę definicję w sensie przybliżonym: ”o ile procent zmieni się $y$ jeśli $x$ zmieni się o $1\%$ ”.

W modelu konsumenta będziemy badać elastyczności popytu:

Definicja 7.4

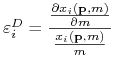Elastyczność dochodowa popytu na dobro $i$ $\varepsilon _{{i}}^{{D}}=\dfrac{\frac{\partial x_{{i}}(\mathbf{p},m)}{\partial m}}{\frac{x_{{i}}(\mathbf{p},m)}{m}}$ ,

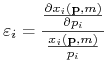elastyczność cenowa popytu na dobro $i$ $\varepsilon _{{i}}=\dfrac{\frac{\partial x_{{i}}(\mathbf{p},m)}{\partial p_{{i}}}}{\frac{x_{{i}}(\mathbf{p},m)}{p_{{i}}}}$ ,

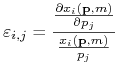elastyczność krzyżowa popytu na dobro $i$ ze względu na cenę dobra $j$ $\varepsilon _{{i,j}}=\dfrac{\frac{\partial x_{{i}}(\mathbf{p},m)}{\partial p_{{j}}}}{\frac{x_{{i}}(\mathbf{p},m)}{p_{{j}}}}$ ,

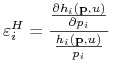elastyczność cenowa popytu Hicksa na dobro $i$ $\varepsilon _{{i}}^{{H}}=\dfrac{\frac{\partial h_{{i}}(\mathbf{p},u)}{\partial p_{{i}}}}{\frac{h_{{i}}(\mathbf{p},u)}{p_{{i}}}}$ .

Ćwiczenie 7.3

Obliczyć elastyczności dochodowe i cenowe (o ile to możliwe) dla doskonałych substytutów, dóbr doskonale komplementarnych, preferencji Cobba-Douglasa i funkcji użyteczności CES $u(x_{1},x_{2})=(x_{1}^{{\rho}}+x_{2}^{{\rho}})^{{\frac{1}{\rho}}}$ .

Z elastycznością dochodową związany jest kolejny podział dóbr normalnych:

Definicja 7.5

Dobro $i$ jest dobrem niezbędnym, jeśli $0<\varepsilon _{{i}}^{{D}}<1$ , a dobrem luksusowym, jeśli $\varepsilon _{{i}}^{{D}}>1$ .

Innymi słowy, dobro niezbędne to takie, na które popyt rośnie wolniej niż dochód (np. chleb), a dobro luksusowe to takie, na które popyt rośnie szybciej niż dochód (np. biżuteria).

Ćwiczenie 7.4

Czy jest możliwe, by:

a) dobro $i$ było niezbędne/luksusowe przy ustalonym wektorze cen dla wszystkich poziomów dochodu?

b) wszystkie dobra konsumowane przez konsumenta były niezbędne?

c) wszystkie dobra konsumowane przez konsumenta były luksusowe?

Ćwiczenie 7.5

Ocenić prawdziwość poniższych zdań w świetle definicji dóbr luksusowych i niezbędnych.

a) Niektórzy bogacze konsumują jedynie dobra luksusowe.

b) Ludzie biedni mogą pozwolić sobie jedynie na konsumpcję dóbr niezbędnych.

Teraz zajmiemy się efektem cenowym, czyli wpływem zmiany ceny rozważanego dobra na popyt na nie. Jak wykazaliśmy uprzednio, efekt cenowy Hicksa jest zawsze mniejszy bądź równy $0$ . Jak jest w przypadku zwykłej funkcji popytu?

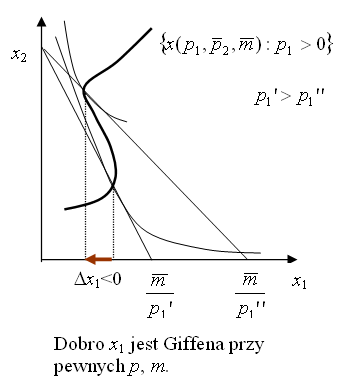
Tym razem też naturalne wydaje się założenie, że popyt na dobro maleje ze wzrostem ceny. Jednak nie zawsze tak jest. Kontrprzykład pochodzi od dziewiętnastowiecznego ekonomisty (czyli, jak należy się domyślać, został zaobserwowany, nie wymyślony), Giffena, skąd nazwa:

Definicja 7.6

Dobro $i$ nazywamy dobrem Giffena, jeśli $\frac{\partial x_{{i}}(\mathbf{p},m)}{\partial p_{{i}}}>0$ dla pewnego $\mathbf{p}$ i $m$ .

Rys. 7.3. Dobro Giffena – $x_{1}$ .

Dobro może być dobrem Giffena zgodnie z naszą teorią, która nie bierze pod uwagę ani tzw. efektu snoba (funkcja użyteczności zależy również od ceny) ani sygnalizacji w przypadku niepełnej informacji (dobro jest drogie, to znaczy zapewne dobrej jakości, której bez tego nie potrafiłbym sam określić – dobro tanie nie może być dobrej jakości). Są to zawsze dobra podrzędne, i to, można powiedzieć, ”bardzo podrzędne”. Giffen podał za przykład ziemniaki.

Przykład 7.1

Ziemniaki stanowią podstawę wyżywienia Patricka O'Briana. Ze względu na korzystny stosunek wartości odżywczej do ceny, może przy ich pomocy spełnić wymagania dietetyczne na w miarę przyzwoitym poziomie, stać go nawet na to, żeby obiad składający się z samych ziemniaków wzbogacić mięsem (wówczas zjada mniej ziemniaków). Kiedy wskutek zarazy ziemiaczanej cena ziemniaka wzrosła, Patricka już nie stać na luksus, jakim jest mięso. Musi kupować więcej ziemniaków (mimo wszystko znacznie tańszych niż mięso), żeby nie głodować.

Aby zakończyć definiowanie różnych pojęć związanych ze znakami efektów, musimy jeszcze wspomnieć o efektach mieszanych, czyli $\frac{\partial x_{{i}}(\mathbf{p},m)}{\partial p_{{k}}}$ dla $i\neq k$ : otrzymamy rozszerzenie klasy doskonałych substytutów i dóbr doskonale komplementarnych.

Definicja 7.7

a) Dobra $i$ i $k$ są substytutami przy cenach $\mathbf{p}$ i wielkości dochodu $m$ , jeśli $\frac{\partial x_{{i}}(\mathbf{p},m)}{\partial p_{{k}}}>0$ i $\frac{\partial x_{{k}}(\mathbf{p},m)}{\partial p_{{i}}}>0$ .

b) Dobra $i$ i $k$ są komplementarne przy cenach $\mathbf{p}$ i wielkości dochodu $m$ , jeśli $\frac{\partial x_{{i}}(\mathbf{p},m)}{\partial p_{{k}}}<0$ i $\frac{\partial x_{{k}}(\mathbf{p},m)}{\partial p_{{i}}}<0$ .

7.2. Własności funkcji popytu

Zobaczmy, co można powiedzieć o efektach i elastycznościach jedynie przy założeniu podstawowych własności: jednorodności stopnia $0$ i prawa Walrasa.

Stwierdzenie 7.1

Jeśli funkcja $x$ jest różniczkowalna i jednorodna stopnia $0$ , to dla każdego $i$

a) $\sum\limits _{{k=1}}^{{n}}\frac{\partial x_{{i}}(\mathbf{p},m)}{\partial p_{{k}}}p_{{k}}+\frac{\partial x_{{i}}(\mathbf{p},m)}{\partial m}m=0$ ,

b) $\sum\limits _{{k=1}}^{{n}}\varepsilon _{{i,k}}+\varepsilon _{{i}}^{{D}}=0$ .

a) Jednorodność stopnia $0$ oznacza, że $x_{{i}}(\mathbf{p},m)=x_{{i}}(t\mathbf{p},tm)$ . Zróżniczkowanie tego równania po $t$ daje nam pożądaną równość.

b) Dzielimy równanie a) przez $x_{{i}}(\mathbf{p},m)$ .

∎

Stwierdzenie 7.2

Jeśli funkcja $x$ jest różniczkowalna i spełnia prawo Walrasa, to

a) $\sum\limits _{{i=1}}^{{n}}\frac{\partial x_{{i}}(\mathbf{p},m)}{\partial p_{{k}}}p_{{i}}+x_{{k}}(\mathbf{p},m)=0$ ,

b) $\sum\limits _{{i=1}}^{{n}}\frac{\partial x_{{i}}(\mathbf{p},m)}{\partial m}p_{{i}}=1$ .

Prawo Walrasa oznacza, że $\mathbf{p}^{{T}}x(\mathbf{p},m)=m$ . Zróżniczkowanie tego równania po $p_{{k}}$ daje nam pożądaną równość a), a po $m$ – b).

∎

Aby móc badać racjonalność konsumenta, kiedy nie znamy jego preferencji, a jedynie jego wybory z pewnych zbiorów budżetowych, interpretowane jako jedyna najlepsza możliwość, służy słaby aksjomat ujawnionych preferencji.

Definicja 7.8

Słaby aksjomat ujawnionych preferencji dla zagadnienia optymalizacji konsumenta (SAUP) to następująca implikacja:

jeżeli $\mathbf{p}^{{T}}x(\mathbf{p}^{{\prime}},m^{{\prime}})\leq m$ i $x(\mathbf{p}^{{\prime}},m^{{\prime}})\neq x(\mathbf{p},m)$ , to $(\mathbf{p}^{{\prime}}\mathbf{)}^{{T}}x(\mathbf{p},m)>m^{{\prime}}$ .

Ćwiczenie 7.6

Czy konsument, którego wybory opisano poniżej nie postąpił nieracjonalnie? (czyli sprawdzić, czy poniższe sytuacje nie są sprzeczne z SAUP).

a) Przy cenach konsument $(2,4)$ zakupił koszyk $(1,2)$ , a przy cenach $(6,3)$ koszyk $(2,1)$ .

b) Przy cenach konsument $(1,1)$ zakupił koszyk $(2,7)$ , a przy cenach $(2,1)$ koszyk $(5,2)$ .

Ćwiczenie 7.7

Mając dane wybory racjonalnego kosumenta w dwóch różnych sytuacjach w przeszłości, oszacować, gdzie znajduje się koszyk, który wybierze obecnie.

W roku 2008, przy cenach $(1,3)$ konsument wybierał koszyk $(\frac{1}{2},\frac{5}{6})$ , a w roku 2009, przy cenach $(3,1)$ koszyk $(\frac{2}{3},1)$ . Obecnie obie ceny są równe $1$ , a konsument dysponuje dochodem $2$ .

Ćwiczenie 7.8

Franek był na trzydniowej wycieczce klasowej. Jego dzienny limit wydatków skrupulatnie wydzielany przez wychowawcę wynosił 10 złotych. Ponieważ w swoim dziesięcioletnim życiu widział już niemalże wszystko, jego zadowolenie z życia w każdym dniu pobytu różniło się w zależności od konsumpcji dwóch niedostępnych dla niego na co dzień potraw: lodów i hamburgerów, których ceny różniły się w zależności od miejsca.

W Wieliczce zjadł dwa lody i dwa hamburgery, płacąc za lody 2 zł za sztukę, a za hamburgery 3 zł za sztukę.

W Krakowie zjadł cztery lody i dwa hamburgery, płacąc odpowiednio 1 i 3 zł.

W Zakopanem zjadł dziesięć lodów i ani jednego hamburgera, przy cenach 1 i 2 zł.

Opowiadał potem, że najbardziej zadowolony był w Krakowie, a najmniej w Zakopanem.

Zbadać racjonalność Franka przy założeniu niezmienności gustów.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.