Zagadnienia
9. Równania Słuckiego i jego uogólnienia – kupno-sprzedaż, podaż pracy, wybór międzyokresowy
9.1. Analiza porównawcza
Przykład 9.1
Skomentować uwagę pewnego ekonomisty ”w krajach biedniejszych elastyczność popytu na żywność jest mniejsza, ponieważ gospodarstwa domowe przeznaczają większą część swoich dochodów na żywność niż w państwach bogatszych”.
Uwaga!: chodzi o wartość bezwzględną elastyczności (podobnie jak w przypadku np. krańcowej stopy substytucji, jeśli jakaś wielkość jest zawsze ujemna, to w porównaniach ekonomiści często zaniedbują znak, nie mówiąc o tym, bo ”i tak wszyscy wiedzą o co chodzi”).
Jest to wniosek z równania Słuckiego: ![]() .
.
![]()
![]() , czyli
, czyli
![]() ,
gdzie
,
gdzie ![]() oznacza część dochodu wydawaną na
żywność. żywność jest dobrem normalnym, więc
oznacza część dochodu wydawaną na
żywność. żywność jest dobrem normalnym, więc ![]() , a elastyczność Hicksa
, a elastyczność Hicksa ![]() jest zawsze ujemna. Jeśli założymy, że elastyczność
Hicksa i elastyczność dochodowa nie zmieniają się, to ze
wzrostem
jest zawsze ujemna. Jeśli założymy, że elastyczność
Hicksa i elastyczność dochodowa nie zmieniają się, to ze
wzrostem ![]() będzie wzrastać wartość bezwzględna
będzie wzrastać wartość bezwzględna ![]() . Przy tych założeniach dochodzimy więc do zupełnie przeciwnego wniosku.
. Przy tych założeniach dochodzimy więc do zupełnie przeciwnego wniosku.
9.2. Zastosowanie równania Słuckiego do szerszej klasy zagadnień podejmowania decyzji przez konsumenta
W dotychczasowych rozważaniach nie braliśmy pod uwagę, skąd się bierze dochód. O ile nie miało to znaczenia przy podejmowaniu decyzji w konkretnych sytuacjach, o tyle jest to istotne, kiedy badamy efekty zmian cen. Co jeśli nasz dochód zależy od cen? W jakich rzeczywistych sytuacjach to ma miejsce?
Konsument może posiadać pewien koszyk, tzw. zasób początkowy (jako dodatkową współrzędną możemy
rozważyć posiadany pieniądz, którego cena stale równa się ![]() , dzięki czemu uzyskujemy rozszerzenie zwykłej optymalizacji
konsumenta). Wówczas konsument może wymienić część
dóbr na inne, przy czym stosunek wymiany wynika z różnicy cen
lub sprzedać część dóbr, by za uzyskane środki
zakupić inne dobra. Jak zauważymy później, do tej klasy
zagadnień należy wybór długości czasu pracy (zagadnienie
podaży pracy), a także wielkość oszczędności w banku
(wybór międzyokresowy).
, dzięki czemu uzyskujemy rozszerzenie zwykłej optymalizacji
konsumenta). Wówczas konsument może wymienić część
dóbr na inne, przy czym stosunek wymiany wynika z różnicy cen
lub sprzedać część dóbr, by za uzyskane środki
zakupić inne dobra. Jak zauważymy później, do tej klasy
zagadnień należy wybór długości czasu pracy (zagadnienie
podaży pracy), a także wielkość oszczędności w banku
(wybór międzyokresowy).
9.2.1. Zasób początkowy: kupowanie i sprzedawanie:
Przyjmujemy, że mój dochód to nie określona z góry suma
pieniędzy w gotówce, lecz pewien koszyk produktów ![]() –
zasób początkowy. Mogę sprzedać część
dóbr, by zakupić za uzyskane pieniądze inne dobra, tak by
zmaksymalizować użyteczność. W pierwszej chwili to
zagadnienie wydaje się zupełnie różne od zagadnienia ”zwykłej” optymalizacji konsumenta.
–
zasób początkowy. Mogę sprzedać część
dóbr, by zakupić za uzyskane pieniądze inne dobra, tak by
zmaksymalizować użyteczność. W pierwszej chwili to
zagadnienie wydaje się zupełnie różne od zagadnienia ”zwykłej” optymalizacji konsumenta.
Aby sprowadzić nasze zagadnienie do tejże postaci, sformułujemy je
nieco inaczej: mogę sprzedać zasób początkowy po cenach
rynkowych, wówczas uzyskam dochód ![]() . Za ten
dochód mogę zakupić nowy koszyk produktów
. Za ten
dochód mogę zakupić nowy koszyk produktów ![]() (w
szczególności nic nie stoi na przeszkodzie, by był to ten sam
koszyk, czyli abym netto nie był sprzedawcą ani nabywcą żadnego z dóbr), tak by zmaksymalizować
użyteczność. Jeśli
(w
szczególności nic nie stoi na przeszkodzie, by był to ten sam
koszyk, czyli abym netto nie był sprzedawcą ani nabywcą żadnego z dóbr), tak by zmaksymalizować
użyteczność. Jeśli ![]() , to jestem nabywcą
netto dobra
, to jestem nabywcą
netto dobra ![]() : w rzeczywistości zakupiłem
: w rzeczywistości zakupiłem ![]() ,
jeśli natomiast
,
jeśli natomiast ![]() , to jestem sprzedawcą netto
dobra
, to jestem sprzedawcą netto
dobra ![]() : w rzeczywistości sprzedałem
: w rzeczywistości sprzedałem ![]()
![]() .
Ograniczenie budżetowe ma postać
.
Ograniczenie budżetowe ma postać ![]() , a zbiór budżetowy
, a zbiór budżetowy ![]() . Zauważmy, że, ponieważ nie
ma żadnych kosztów transakcji, takie podejście jest
równoważne wyjściowemu problemowi
. Zauważmy, że, ponieważ nie
ma żadnych kosztów transakcji, takie podejście jest
równoważne wyjściowemu problemowi
Nasz popyt to ![]() . Jeżeli chcemy
badać efekt zmiany ceny dóbr, musimy pamiętać, że występuje ona w obu argumentach
. Jeżeli chcemy
badać efekt zmiany ceny dóbr, musimy pamiętać, że występuje ona w obu argumentach ![]() .
.
Całkowita zmiana popytu na dobro ![]() spowodowana zmianą ceny dobra
spowodowana zmianą ceny dobra ![]() jest więc równa:
jest więc równa:
![]() .
.
Korzystając ze ”zwykłego” ciągłego równania Słuckiego, otrzymujemy więc
![]() –
równanie Słuckiego dla naszego zagadnienia.
–
równanie Słuckiego dla naszego zagadnienia.
Efekt substytucyjny nie zmienia się, natomiast drugi z efektów to efekt majątkowy. Jego znak, oprócz tego, czy dobro jest normalne, czy podrzędne, zależy też od tego, czy jestem sprzedawcą czy nabywcą netto dobra, którego cena uległa zmianie.
Warto zwrócić uwagę na jeszcze jedną rzecz: równoczesne
przemnożenie cen wszystkich produktów przez tę samą liczbę
dodatnią nie zmienia zagadnienia. Stąd jeśli rozważamy
model z dwoma dobrami, łatwo nam badać wpływ na popyt na dobro
zmiany ceny drugiego dobra: podwyżka ceny drugiego dobra jest
równoważna obniżce ceny pierwszego, a więc nie musimy
korzystać z ”krzyżowych” efektów substytucyjnych ![]() , których znak jest trudny do
określenia.
, których znak jest trudny do
określenia.
Zobaczmy, korzystając z równania Słuckiego, jak zmieni się
popyt na dobro ![]() , jeśli zmianie uległa tylko cena
, jeśli zmianie uległa tylko cena ![]() – wzrosła:
– wzrosła:
Jeśli ![]() jest dobrem normalnym, to nabywca netto dobra
jest dobrem normalnym, to nabywca netto dobra ![]() zmniejszy
jego konsumpcję (będzie kupował mniej, a nawet stanie się
sprzedawcą netto), natomiast nic nie można powiedzieć o
sprzedawcy netto; a jeśli
zmniejszy
jego konsumpcję (będzie kupował mniej, a nawet stanie się
sprzedawcą netto), natomiast nic nie można powiedzieć o
sprzedawcy netto; a jeśli ![]() jest dobrem podrzędnym, to na
odwrót.
jest dobrem podrzędnym, to na
odwrót.
Ćwiczenie 9.1
Właściel browaru konsumuje jabłka i piwo. Ma funkcję użyteczności o krańcowej stopie substytucji ![]() . Obecnie cena zarówno cena jabłek jak i cena piwa wynosi
. Obecnie cena zarówno cena jabłek jak i cena piwa wynosi ![]() , a nasz browarnik ma kilogram jabłek i 1000 butelek piwa.
, a nasz browarnik ma kilogram jabłek i 1000 butelek piwa.
Jaki będzie efekt
a) podwyżki cen jabłek;
b) podwyżki cen piwa?
Jaką cześć tych zmian przypiszemy efektowi substytucyjnemu, a jaką majątkowemu (z ciągłego równania Słuckiego)?
9.2.1.1. Podaż pracy
Choć na pierwszy rzut oka nie widać związku, wybór, ile godzin będę pracował (a co za tym idzie – ile zarobię), a ile godzin odpoczywał, jest przykładem zagadnienia wyboru przy dochodzie w postaci zasobu początkowego.
Najpierw zauważmy, że praca raczej nie jest ”dobrem” w rozumieniu ekonomicznych. Co najwyżej pieniądze, które za nią otrzymujemy, albo status społeczny, poczucie bezpieczeństwa… Na pewno większa liczba przepracowanych godzin nie zwiększa naszej użyteczności, przeciwnie: zmniejsza ją. Jeżeli weźmiemy pod uwagę przeciwieństwo pracy – odpoczynek – będzie to już dobro. Przyjmujemy, że odpoczynek jest dobrem normalnym.
W okresie, na jaki podejmujemy decyzję (doba, tydzień, miesiąc…) istnieje maksymalna liczba godzin, którą możemy
podzielić na pracę i odpoczynek. Nie musi to być ![]() godziny na
dobę, może to być liczba mniejsza określająca, ile
jesteśmy w stanie pracować. Oznaczmy tę liczbę przez
godziny na
dobę, może to być liczba mniejsza określająca, ile
jesteśmy w stanie pracować. Oznaczmy tę liczbę przez ![]() . Jeżeli pracę oznaczamy przez
. Jeżeli pracę oznaczamy przez ![]() , to odpoczynek będzie
wynosił
, to odpoczynek będzie
wynosił ![]() . Stawka płacy wynosi
. Stawka płacy wynosi ![]() , będzie to zatem cena
odpoczynku. W modelu mamy jeszcze drugie dobro: konsumpcję
, będzie to zatem cena
odpoczynku. W modelu mamy jeszcze drugie dobro: konsumpcję ![]() , liczoną w pieniądzu, o cenie
, liczoną w pieniądzu, o cenie ![]()
W najprostszym przykładzie nie dysponujemy żadnym dochodem pozapłacowym, czyli ![]() , a
, a ![]() . Dysponujemy jedynie
odpoczynkiem w ilości
. Dysponujemy jedynie
odpoczynkiem w ilości ![]() , który sprzedajemy, by za uzyskany
dochód kupić konsumpcję i odpoczynek, co daje ograniczenie
budżetowe
, który sprzedajemy, by za uzyskany
dochód kupić konsumpcję i odpoczynek, co daje ograniczenie
budżetowe ![]() – jest to przekształcone wyliczenie wypłaty za pracę.
– jest to przekształcone wyliczenie wypłaty za pracę.
Ćwiczenie 9.2
Ryszard pracuje na budowie i zarabia na rękę ![]() zł za godzinę. Tygodniowo dysponuje
zł za godzinę. Tygodniowo dysponuje ![]() godzinami, ktore może podzielić między pracę a odpoczynek. Jego funkcja użyteczności dotycząca wyboru pieniędzy na konsumpcję i czasu wolnego to
godzinami, ktore może podzielić między pracę a odpoczynek. Jego funkcja użyteczności dotycząca wyboru pieniędzy na konsumpcję i czasu wolnego to ![]() .
.
a) Obliczyć, ile Ryszard będzie pracował i ile odpoczywał i zilustrowac jego zagadnienie podaży pracy na wykresie.
b) Rząd podniósł podatki, aby mieć pieniądze na sfinansowanie planowanych wydatków wskutek czego teraz Ryszard dostaje na rękę 4zł za godzinę. Równocześnie rząd chce wprowadzić program pomocy dla najniżej zarabiających w ramach którego postanowił wypłacić zarabiającym mniej niż 6zł za godzinę różnicę pomiędzy ich zarobkami sprzed wprowadzenia podatków a obecnymi zarobkami.
Ile w tej sytuacji Ryszard by pracował i ile miał na konsumpcję? Czy oceniłby obecną sytuację jako lepszą, czy jako gorszą niż z punktu a)? Czy jest tu jakaś niejasność?
c) Rząd jednak skonsultował się z ekonomistą, który uznał, że aby uniknąć niekorzystnych efektów na rynku pracy, lepiej zwrócić jedynie różnicę pomiędzy zarobkami po zmianie a poprzednimi przy liczbie godzin pracy sprzed wprowadzenia podatku.
Ile Ryszard przy tym programie by pracował i ile miał na konsumpcję? Czy oceniłby obecną sytuację jako lepszą, czy jako gorszą niż z punktu a)?
Uwaga 9.1
Jeśli rozważamy inną płacę za nadgodziny niż za normowany czas pracy, podatki od pewnego poziomu dochodu i tym podobne, wówczas ograniczenie budżetowe będzie łamaną, a cena odpoczynku będzie się zmieniać.
Ćwiczenie 9.3
Marek ma 60 godzin tygodniowo do podziału pomiędzy pracę a odpoczynek. Pracuje jako goniec i otrzymuje 10 zł za godzinę czasu normowanego, czyli do 40 godzin, a 15 zł za nadgodziny. Jego funkcja użyteczności zagadnienia podaży pracy to ![]() .
.
Jak wygląda ograniczenie budżetowe Marka?
Ile będzie pracował, a ile odpoczywał? Czy/ile będzie pracował w nadgodzinach?
Ćwiczenie 9.4
Joanna projektuje biżuterię artystyczną i otrzymuje 20zł za godzinę. Do podziału na pracę i odpoczynek ma 90 godzin tygodniowo. Jej funkcja użyteczności to ![]() .
.
a) Ile będzie pracować i ile konsumować w tym przypadku?
b) Wybory wygrali populiści pod hasłem ”zabierać bogatym, rozdawać biednym”.
Planują, żeby na wszystkich zarabiających powyżej 800zł tygodniowo nałożyć podatek w wysokości ![]() . Narysować nowe ograniczenie budżetowe Joanny i naszkicować istotne dla zagadnienia krzywe obojętności. Jak zmieni się jej wybór?
. Narysować nowe ograniczenie budżetowe Joanny i naszkicować istotne dla zagadnienia krzywe obojętności. Jak zmieni się jej wybór?
c) Po miesiącu populiści wycofali się z tego projektu i teraz ![]() podatek naliczany jest jedynie od kwoty powyżej 800zł.
podatek naliczany jest jedynie od kwoty powyżej 800zł.
Spróbowac uzasadnić, dlaczego się wycofali (chodziło o względy czysto ekonomiczne).
Narysować ograniczenie budżetowe Joanny w tej sytuacji i naszkicować istotne dla zagadnienia krzywe obojętności. Jak zmieni się jej wybór?
Równanie Słuckiego dla czasu wolnego będzie miało postać:
![]()
![]() .
.
Mamy do czynienia z dwoma przeciwstawnymi efektami: ujemnym substytucyjnym i dodatnim majątkowym, więc nie można powiedzieć, który z nich przeważy. Możliwe jest zarówno, że ze wzrostem stawki płacy będziemy więcej pracować (mniej odpoczywać) ze względu na to że odpoczynek stanie się relatywnie droższy, jak i że będziemy mniej pracować (więcej odpoczywać), bo będziemy mogli sobie na to pozwolić. Zazwyczaj ekonomiści uważają, że przy wysokich stawkach mamy do czynienia z tą drugą sytuacją. Dlatego, by motywować pracowników do dłuższej pracy, wprowadza się wyższą stawkę za nadgodziny.
Ćwiczenie 9.5
Uogólnić równanie Słuckiego podaży pracy na sytuację, kiedy pracownik posiada pewien dochód pozapłacowy.
Ćwiczenie 9.6
Janka utrzymuje się z pracy w kuchni i z pieniędzy stanowiących jej honorarium autorskie od wydanej uprzednio książki. Zawsze kiedy jej honorarium autorkie jest niższe, Janka pracuje w kuchni dłużej.
Co się będzie działo z liczbą godzin przepracowanych przez Jankę w następujących sytuacjach:
a) na dochód płacowy rząd nakłada proporcjonalny podatek dochodowy;
b) taki sam proporcjonalny podatek nakłada zarówno na dochód płacowy, jak i pozapłacowy;
c) na dochód płacowy rząd nakłada proporcjonalny podatek dochodowy i równocześnie funduje stypendium w wysokości równej podatkowi naliczonemu od uprzednich zarobków.
9.2.2. Wybór międzyokresowy
W najprostszym ujęciu mamy dwa okresy (chociaż może być ich
więcej), dla uproszczenia będziemy nazywać je ”dziś” i
”jutro”; i oznaczać przez ![]() i
i ![]() .
.
W okresie ![]() mam dochód deterministyczny
mam dochód deterministyczny ![]() i wybieram poziom
konsumpcji
i wybieram poziom
konsumpcji ![]() . Konsumpcje w obu okresach są dobrami normalnymi.
Swój dochód pomiędzy okresami mogę przenosić korzystając z banku przy stopie procentowej
. Konsumpcje w obu okresach są dobrami normalnymi.
Swój dochód pomiędzy okresami mogę przenosić korzystając z banku przy stopie procentowej ![]() : mogę oszczędzać
– konsumować mniej niż zarabiam w dziś, bądź zadłużać się – wziąć pożyczkę pod zastaw
przyszłego dochodu, czyli konsumować dziś więcej niż
zarabiam. W zagadnieniu wyboru międzyokresowego zakładamy, że nie
można wziąć pożyczki, której się nie spłaci oraz,
dla uproszczenia, że stopa procentowa jest jednakowa dla kredytów i
lokat tzn. nie ma marży.
: mogę oszczędzać
– konsumować mniej niż zarabiam w dziś, bądź zadłużać się – wziąć pożyczkę pod zastaw
przyszłego dochodu, czyli konsumować dziś więcej niż
zarabiam. W zagadnieniu wyboru międzyokresowego zakładamy, że nie
można wziąć pożyczki, której się nie spłaci oraz,
dla uproszczenia, że stopa procentowa jest jednakowa dla kredytów i
lokat tzn. nie ma marży.
Ogranicznie budżetowe, jak we wszystkich zagadnieniach dochodu w postaci zasobu początkowego, może mieć nieskończenie wiele równoważnych postaci, jednak w przypadku zagadnienia wyboru międzyokresowego dwie z nich mają interpretację:
![]() – w terminach wartości
przyszłej: wartość przyszła strumienia konsumpcji jest
równa wartości przyszłej strumienia dochodów – tyle byśmy
mieli jutro, gdybyśmy odłożyli do banku;
– w terminach wartości
przyszłej: wartość przyszła strumienia konsumpcji jest
równa wartości przyszłej strumienia dochodów – tyle byśmy
mieli jutro, gdybyśmy odłożyli do banku;
![]() – w terminach wartości obecnej: wartość obecna strumienia konsumpcji jest
równa wartości obecnej strumienia dochodów – tyle pieniędzy
moglibyśmy uzyskać dziś pod zastaw naszych dochodów.
– w terminach wartości obecnej: wartość obecna strumienia konsumpcji jest
równa wartości obecnej strumienia dochodów – tyle pieniędzy
moglibyśmy uzyskać dziś pod zastaw naszych dochodów.
Zasób początkowy to ![]() i
i ![]() .
.
Ćwiczenie 9.7
Janek dysponuje dochodem w wysokości 10000zł w tym roku i 10000zł w przyszłym. Stopa procentowa wynosi ![]() .
.
a) Jaka jest wartość obecna jego dochodu (przy założeniu, że otrzymuje pieniądze zawsze na początku roku).
b) Narysować jego ograniczenie budżetowe, przy założeniu, że jednostka konsumpcji w każdym z okresów kosztuje 1zł.
c) Funkcja użyteczności konsumpcji w czasie to ![]() .
.
Ile Janek skonsumuje w tym, a ile w przyszłym roku? Czy będzie pożyczkodawcą, czy pożyczkobiorcą?
d) Jak zmieni się odpowiedź, jeśli mamy inflację, na skutek której cena jednostki konsumpcji w przyszłym roku wzrośnie do 2zł?
Ćwiczenie 9.8
Mieszkańcy pewnej odległej wyspy żyją jedynie z uprawy ryżu. W tym roku zebrali 100 worków ryżu, który mogą albo skonsumować natychmiast, albo zmagazynować na zimę.
Plagą wyspy są szczury, które zjadają połowę plonów z magazynu.
a) Ile mieszkańcy będą konsumować natychmiast, a ile w zimie, jeśli mają funkcję użyteczności konsumcji w czasie, której moduł z krańcowej stopy substytucji ![]() przez
przez ![]() wynosi
wynosi ![]() ?
?
b) Na wyspę przybył okręt kupiecki i widząc zapotrzebowanie, zaproponował sprzedaż okrętowego szczurołapa – bardzo łownego kota, którego zakup spowoduje, że szczury zjedzą nie więcej niż ![]() zmagazynowanych zbiorów. Ile maksymalnie mieszkańcy wsi zapłaciliby za kota (licząc w workach ryżu)?
zmagazynowanych zbiorów. Ile maksymalnie mieszkańcy wsi zapłaciliby za kota (licząc w workach ryżu)?
Ćwiczenie 9.9
Staszek dysponuje dochodem w wysokości 10000zł w tym roku i 20000zł w przyszłym. System bankowy oferuje dwie różne stopy procentowe: dla kretytów ![]() i dla lokat
i dla lokat ![]() .
.
a) Jaka jest wartość obecna jego dochodu (przy założeniu, że otrzymuje pieniądze zawsze na początku roku). Jaka jest wartość przyszła jego dochodu?
b) Narysować jego ograniczenie budżetowe, przy założeniu, że jednostka konsumpcji w każdym z okresów kosztuje 1zł.
c) Funkcja użyteczności konsumpcji w czasie to ![]() .
.
Ile skonsumuje w tym, a ile w przyszłym roku? Czy będzie pożyczkodawcą, czy pożyczkobiorcą?
Jeżeli badamy wpływ wzrostu stopy procentowej na konsumpcję
dziś i jutro, wygodnie jest użyć ograniczenia budżetowego w
terminach wartości przyszłej dla ![]() (wówczas cena
(wówczas cena ![]() ,
, ![]() ) i wartości obecnej dla
) i wartości obecnej dla ![]() (
(![]() ,
, ![]() ) i skorzystać z równania Słuckiego dla zmiany ceny tego
samego dobra:
) i skorzystać z równania Słuckiego dla zmiany ceny tego
samego dobra: ![]() .
.
Ponieważ ![]() i
i ![]() , a
konsumpcje w obu okresach są normalne, to pożyczkodawca (ten, kto
oszczędza) będzie konsumował jutro więcej, natomiast nie
wiadomo, jak będzie z jego konsumpcję dziś; pożyczkobiorca będzie konsumował dziś mniej, natomiast nie wiadomo, co będzie
z jego konsumpcją jutro – może zacząć oszczędzać,
przez co ją zwiększy, a może zmniejszyć, jeśli
pożycza więcej, aby za bardzo nie zmniejszyć konsumpcji dziś.
, a
konsumpcje w obu okresach są normalne, to pożyczkodawca (ten, kto
oszczędza) będzie konsumował jutro więcej, natomiast nie
wiadomo, jak będzie z jego konsumpcję dziś; pożyczkobiorca będzie konsumował dziś mniej, natomiast nie wiadomo, co będzie
z jego konsumpcją jutro – może zacząć oszczędzać,
przez co ją zwiększy, a może zmniejszyć, jeśli
pożycza więcej, aby za bardzo nie zmniejszyć konsumpcji dziś.
9.2.3. Statyka porównawcza – przykłady
Przykład 9.2
Podniesiono cenę żywności z ![]() do
do ![]() . Emeryci i
renciści przeznaczają około
. Emeryci i
renciści przeznaczają około ![]() swoich dochodów na
żywność. O ile powinniśmy podnieść ich dochody, aby
mieć pewność, że ich sytuacja nie pogorszy się. Czy
należy się spodziewać, że ich sytuacja poprawi się?
swoich dochodów na
żywność. O ile powinniśmy podnieść ich dochody, aby
mieć pewność, że ich sytuacja nie pogorszy się. Czy
należy się spodziewać, że ich sytuacja poprawi się?
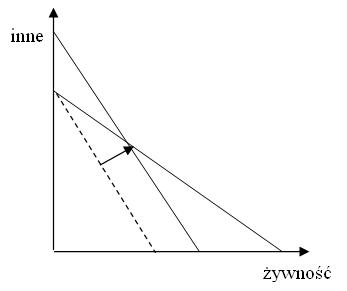
Jeśli nie wiemy nic o użyteczności, musimy zwiększyć
dochód o tyle, aby uprzednio wybierany koszyk był na nowym
ograniczeniu budżetowym, czyli o ![]() .
Wówczas użyteczność na pewno nie zmniejszy się, a
jeśli konsumenci wybiorą inny koszyk, wówczas się zwiększy. Z tą drugą sytuacją będziemy mieć zawsze do
czynienia, jeśli funkcja użyteczności jest
różniczkowalna.
.
Wówczas użyteczność na pewno nie zmniejszy się, a
jeśli konsumenci wybiorą inny koszyk, wówczas się zwiększy. Z tą drugą sytuacją będziemy mieć zawsze do
czynienia, jeśli funkcja użyteczności jest
różniczkowalna.
Przykład 9.3
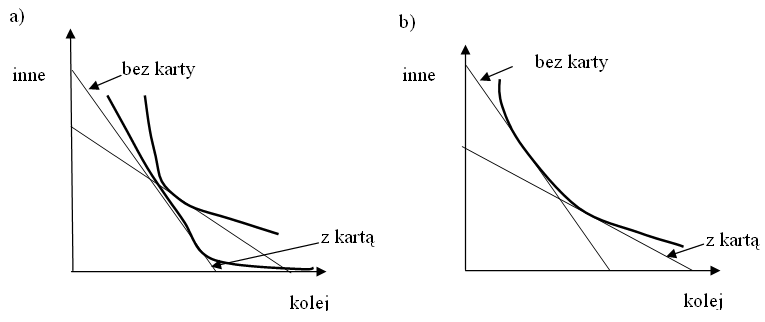
W ramach akcji marketingowej PKP postanowiły wprowadzić roczne karty podróżne dla studentów, które upoważniają do zniżki przy zakupie wszystkich biletów. Czy jeśli student kupi taką kartę, to będzie więcej korzystał z usług PKP? Czy student, któremu wszystko jedno, czy kupić kartę czy nie, będzie więcej wydawał na kolej, jeśli ją wykupi?
Odpowiedź na pierwsze pytanie brzmi ”nie”, a na drugie ”tak”.
Załóżmy, że podróże koleją są dla studenta dobrem normalnym (przy jego poziomie dochodu samolot czy taksówka na długą trasę raczej rzadko wchodzi w grę). Efekt substytucyjny jest dodatni, efekt dochodowy też, ale dochód się zmniejsza przez to, że student musi wykupić kartę, więc teoretycznie może się zdarzyć, że będzie jeździł mniej.
Odpowiedź na drugie pytanie brzmi ”tak”, ponieważ ”jest mu wszystko jedno” oznacza, że ta sama krzywa obojętności jest styczna do obu ograniczeń budżetowych, więc może być styczna do ograniczenia budżetowego odpowiadającego wykupowi karty tylko w jego fragmencie, który dotychczas nie był dostępny, co oznacza zwiększenie przejazdów koleją.
Przykład 9.4
W pewnym zakładzie stawki płac wynoszą ![]() zł za godzinę,
tydzień roboczy ma pięć dni po osiem godzin. Każdy pracownik
może brać nadgodziny, płatne
zł za godzinę,
tydzień roboczy ma pięć dni po osiem godzin. Każdy pracownik
może brać nadgodziny, płatne ![]() zł za godzinę, jednak nie
więcej niż
zł za godzinę, jednak nie
więcej niż ![]() tygodniowo. Przeciętny pracownik bierze
tygodniowo. Przeciętny pracownik bierze ![]() nadgodzin tygodniowo. Zakład pracy płaci składki ZUS w wysokości
nadgodzin tygodniowo. Zakład pracy płaci składki ZUS w wysokości ![]() zł tygodniowo na pracownika. Związek zawodowy proponuje
zrównać stawki płacy zasadniczej i za nadgodziny na poziomie
zł tygodniowo na pracownika. Związek zawodowy proponuje
zrównać stawki płacy zasadniczej i za nadgodziny na poziomie ![]() zł. Przeanalizować tę propozycję.
zł. Przeanalizować tę propozycję.
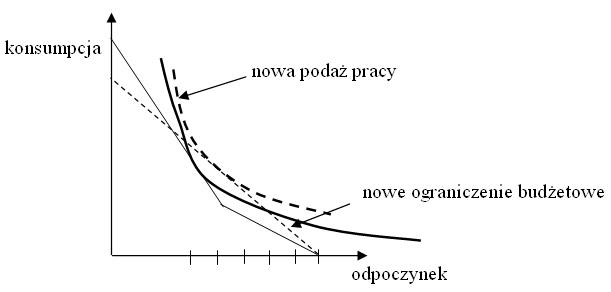
Zakładamy, że zakład pracy chce utrzymać podaż pracy
pracowników na tym samym poziomie co przed zmianą. Chociaż przy
tym samym poziomie nadgodzin co poprzednio, przeciętny pracownik
otrzymywałby taką samą wypłatę, należy oczekiwać,
że jego podaż pracy zmniejszy się (zwiększy się popyt na
odpoczynek), gdyż mamy tu do czynienia jedynie z efektem substytucyjnym,
dodatnim w przypadku odpoczynku, którego cena relatywnie obniży się (jeśli pracujemy powyżej ![]() godzin).
godzin).
Aby utrzymać ten sam poziom podaży pracy, trzeba byłoby zatrudnić nowych pracowników, którzy wypracowaliby brakujące godziny. To jednak zwiększy koszty – za każdego nowego pracownika trzeba dodatkowo zapłacić ZUS.
9.3. Od funkcji popytu do preferencji
Jak odtworzyć relację preferencji, jeżeli mamy dane mamy jedynie to, co można uzyskać z badań rynku: funkcję popytu.
Można to robić ”na raty” albo bezpośrednio.
Wiemy, że przy założeniach o regularności, jeżeli mamy jedną z funkcji ![]() lub
lub ![]() , to można z nich odtworzyć pozostałe
funkcje modelu konsumenta. Mając funkcję
, to można z nich odtworzyć pozostałe
funkcje modelu konsumenta. Mając funkcję ![]() lub
lub ![]() , przy pewnych
założeniach o regularności łatwo uzyskamy również funkcję użyteczności odzwierciedlającą wyjściowe
preferencje.
, przy pewnych
założeniach o regularności łatwo uzyskamy również funkcję użyteczności odzwierciedlającą wyjściowe
preferencje.
Stwierdzenie 9.1
Przy standartowych założeniach modelu konsumenta i jeżeli funkcja ![]() jest wklęsła:
jest wklęsła:
a) jeżeli ![]() jest niejawną funkcją użyteczności, to dla
każdego
jest niejawną funkcją użyteczności, to dla
każdego ![]() zachodzi równość
zachodzi równość ![]() ;
;
b) Zbiory niegorsze niż ![]() spełniają
spełniają ![]() a krzywe obojętności
a krzywe obojętności ![]()
![]()
Tak więc wystarczy wystarczy znaleźć pewną funkcję ![]() lub
lub ![]() , aby znaleźć funkcję użyteczności. Jak jednak
uzyskać jedną z tych funkcji, mając daną jedynie funkcję
, aby znaleźć funkcję użyteczności. Jak jednak
uzyskać jedną z tych funkcji, mając daną jedynie funkcję
![]() ?
?
Z lematu Shepharda ![]() .
.
Stąd funkcja wydatków jako funkcja cen przy ustalonym poziomie
użyteczności ![]() opisana jest układem równań
różniczkowych cząstkowych pierwszego rzędu:
opisana jest układem równań
różniczkowych cząstkowych pierwszego rzędu:
![]() dla
dla ![]() z warunkiem początkowym
z warunkiem początkowym ![]() (czyli
(czyli ![]() takie, że
takie, że ![]() – musimy przypisać
jakiś poziom użyteczności wyjściowemu popytowi).
– musimy przypisać
jakiś poziom użyteczności wyjściowemu popytowi).
W przypadku dwóch dóbr, korzystając z jednorodności stopnia ![]() funkcji
funkcji ![]() układ można zredukować do jednego równania
zwyczajnego:
układ można zredukować do jednego równania
zwyczajnego:
![]() ,
czyli, w uproszczonej postaci:
,
czyli, w uproszczonej postaci:
![]() z warunkiem początkowym
z warunkiem początkowym ![]() .
.
Rozwiązanie będzie miało wszystkie wymagane własności
funkcji wydatków i istnieje przy dość słabych założeniach regularności funkcji ![]() .
.
Jeżeli dóbr jest więcej niż ![]() , to problemu nie da się
zredukować do równania różniczkowego zwyczajnego. Warunek
konieczny istnienia funkcji
, to problemu nie da się
zredukować do równania różniczkowego zwyczajnego. Warunek
konieczny istnienia funkcji ![]() dwukrotnie różniczkowalnej jako
funkcja cen jest oczywisty: macierz substytucji musi być symetryczna:
dwukrotnie różniczkowalnej jako
funkcja cen jest oczywisty: macierz substytucji musi być symetryczna: ![]() dla każdego
dla każdego ![]() . Jest to równocześnie warunek
dostateczny (warunki całkowalności). Rozwiązanie ma własności
. Jest to równocześnie warunek
dostateczny (warunki całkowalności). Rozwiązanie ma własności ![]() i macierz drugiej pochodnej jest równa macierzy
substytucji.
i macierz drugiej pochodnej jest równa macierzy
substytucji.
To kończy procedurę postępowania w przypadku gdy mamy regularną funkcję popytu. Nie będziemy jednak dokładniej analizaować tego zagadnienia.
Jeżeli ![]() nie jest różniczkowalna,
pozostaje nam metoda bezpośrednia – konstrukcja relacji preferencji
przy użyciu ujawnionych preferencji. Ponieważ wiemy, że relacja
preferencji jest racjonalna, musimy rozszerzyć definicję ujawnionej
preferencji o informacje, które możemy wyciągnąć z
przechodniości. Wówczas uzyskamy relację pośredniej
ujawnionej preferencji.
nie jest różniczkowalna,
pozostaje nam metoda bezpośrednia – konstrukcja relacji preferencji
przy użyciu ujawnionych preferencji. Ponieważ wiemy, że relacja
preferencji jest racjonalna, musimy rozszerzyć definicję ujawnionej
preferencji o informacje, które możemy wyciągnąć z
przechodniości. Wówczas uzyskamy relację pośredniej
ujawnionej preferencji.
Definicja 9.1
Mówimy, że koszyk ![]() jest pośrednio jawnie ściśle
preferowany przed
jest pośrednio jawnie ściśle
preferowany przed ![]() , jeśli istnieje liczba naturalna
, jeśli istnieje liczba naturalna ![]() i ciąg
par
i ciąg
par ![]() , taki że
, taki że ![]()
![]() dla
dla ![]() ,
, ![]() i
i ![]()
Relacja pośredniej jawnej preferencji jest domknięciem zwykłej (używa się też dla porównania słowa bezpośredniej) jawnej preferencji ze względu na przechodniość.
Mocny aksjomat ujawnionych preferencji mówi, że jeżeli ![]() jest
pośrednio jawnie preferowany przed
jest
pośrednio jawnie preferowany przed ![]() , to
, to ![]() nie może być
bezpośrednio jawnie preferowany przed
nie może być
bezpośrednio jawnie preferowany przed ![]() .
.
Definicja 9.2
Mocny (silny) aksjomat ujawnionych preferencji
Funkcja popytu spełnia mocny aksjomat ujawnionych preferencji,
że dla dowolnych koszyków ![]() i
i ![]() , jeśli
, jeśli ![]() jest
pośrednio ściśle jawnie preferowany przed
jest
pośrednio ściśle jawnie preferowany przed ![]() to
to ![]() (gdzie
(gdzie ![]() ).
).
Stwierdzenie 9.2
Jeżeli funkcja popytu Walrasa ![]() spełnia mocny aksjomat ujawnionych
preferencji, to istnieje racjonalna relacja preferencji racjonalizująca
spełnia mocny aksjomat ujawnionych
preferencji, to istnieje racjonalna relacja preferencji racjonalizująca ![]() , taka że
, taka że ![]() koszyk
koszyk
![]() jest lepszy od
jest lepszy od ![]() .
.