3. Zadania, I

1. Rozważamy polisę emerytalną dla (x). Polega ona na tym, że przez następne $m$ lat będzie on płacił co rok składkę netto $P$ . Po dożyciu wieku $x+m$ zacznie otrzymywać emeryturę w postaci renty dożywotniej w stałej wysokości $1$ zł (na początku każdego roku). Gdy umrze przed osiągnięciem wieku $x+m$ nic nie będzie wypłacone. Niech $L$ oznacza stratę ubezpieczyciela netto na moment wystawienia polisy. Wykazać, że zdarzenie $\{ L<0\}$ opisuje wzór

$v^{{K+1}}>1-(P+1)(1-v^{m})$

Rozwiązanie. Strata $L$ wyraża się wzorem

$L=\left\{\begin{array}[]{lll}-P(1+v+\ldots+v^{K}),&\mbox{ dla }&K<m\\ (v^{m}+\ldots v^{K})-P(1+v+\ldots+v^{{m-1}}),&\mbox{ dla }&K\ge m\end{array}\right.$

Jeśli $K<m$ to zawsze $L<0$ . Jeśli natomiast $K\ge m$ to $L<0$ oznacza, że

$\frac{v^{m}-v^{{K+1}}}{d}<P\frac{1-v^{m}}{d}$

a to jest równoważne wzorowi z treści zadania.

2. Niech $\bar{A}_{{x:\overline{m}\mid}}^{1}(\delta)$ oznacza składkę $\bar{A}_{{x:\overline{m}\mid}}^{1}$ obliczoną z użyciem technicznej intensywności oprocentowania $\delta>0$ . Obliczyć $\Delta\delta$ które spełnia równanie

$\bar{A}_{{x:\overline{m}\mid}}^{1}(\delta)=\bar{A}_{{x+\frac{1}{12}:\overline{m+\frac{1}{12}}\mid}}^{1}(\delta+\Delta\delta)$

jeżeli dane są wartości:

$\bar{A}_{{x:\overline{m}\mid}}^{1}=0,131763,\bar{A}_{{x:\overline{m}\mid}}^{{\mbox{ 1}}}=0,0768021,(\bar{I}\bar{A})_{{x:\overline{m}\mid}}^{1}=3,0173,$

$\mu _{x}=0,002,\mu _{{x+m}}=0,05,\delta=\ln(1,05)=0,04879$

(obliczone przy podanej wartości $\delta$ ).

Rozwiązanie. Zastępując przyrost funkcji różniczką otrzymujemy następujące równanie na $\Delta\delta$

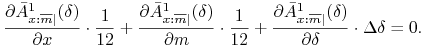$\frac{\partial\bar{A}^{1}_{{x:\overline{m}\mid}}(\delta)}{\partial x}\cdot\frac{1}{12}+\frac{\partial\bar{A}^{1}_{{x:\overline{m}\mid}}(\delta)}{\partial m}\cdot\frac{1}{12}+\frac{\partial\bar{A}^{1}_{{x:\overline{m}\mid}}(\delta)}{\partial\delta}\cdot\Delta\delta=0.$

Obliczymy najpierw potrzebne pochodne cząstkowe.

Tu prosze poprawic wzor

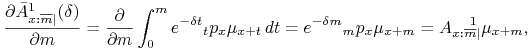$\frac{\partial\bar{A}^{1}_{{x:\overline{m}\mid}}(\delta)}{\partial m}=\frac{\partial}{\partial m}\int _{0}^{m}e^{{-\delta t}}\mbox{}_{t}p_{x}\mu _{{x+t}}\, dt=e^{{-\delta m}}\mbox{}_{m}p_{x}\mu _{{x+m}}=A_{{x:\overline{m}\mid}}^{{\ \ \ 1}}\mu _{{x+m}},$

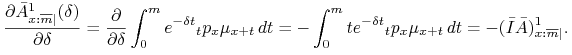$\frac{\partial\bar{A}^{1}_{{x:\overline{m}\mid}}(\delta)}{\partial\delta}=\frac{\partial}{\partial\delta}\int _{0}^{m}e^{{-\delta t}}\mbox{}_{t}p_{x}\mu _{{x+t}}\, dt=-\int _{0}^{m}te^{{-\delta t}}\mbox{}_{t}p_{x}\mu _{{x+t}}\, dt=-(\bar{I}\bar{A})_{{x:\overline{m}\mid}}^{1}.$

Zatem $\Delta\delta$ spełnia równanie

$\frac{1}{12}[0,131763(0,002+0,04879)+0,0768021\cdot 0,05-0,002]+\frac{1}{12}0,0768021\cdot 0,05-3,0173\Delta\delta=0$

skąd otrzymujemy ostatecznie $\Delta\delta=???$ .

3. Niech $P_{x}$ oznacza tradycyjnie regularną coroczną składkę płatną aż do śmierci za ubezpieczenie osoby w wieku $x$ , które wypłaci $1$ zł na koniec roku śmierci. Załóżmy, że $x$ jest liczbą całkowitą a $u\in(0,1)$ . Udowodnić, że przy założeniu UDD składka $P_{{x+u}}$ wyraża się przez składki $P_{x}$ oraz $P_{{x+1}}$ następującym wzorem:

$P_{{x+u}}=w_{x}\cdot P_{x}+w_{{x+1}}\cdot P_{{x+1}}$

gdzie $w_{{x+1}}=1-w_{x}$ oraz

$w_{x}=\frac{(1-u)(P_{{x+1}}+d)}{(1-u)(P_{{x+1}}+d)+(u-uq_{x})(P_{x}+d)}$

4. Rozważamy ubezpieczenie na życie ciągłe dla (35). Wypłaci ono $1$ zł w chwili śmierci. Natomiast składka netto będzie płacona w postaci renty dożywotniej ciągłej z odpowiednio dobraną intensywnością. Obliczyć $\pi^{s}(10)$ tzn. intensywność oszczędnościowej części składki po 10 latach. Dane są:

$i=5\%,M_{{35}}=3776,D_{{35}}=17236,M_{{45}}=3181,D_{{45}}=10091,p_{{45}}=0,992.$

Uwaga! Należy skorzystać z założenia UDD.

Rozwiązanie. Skorzystamy ze wzoru

$\pi^{s}(t)=V^{{\prime}}(t)-\delta V(t).$

Mamy

$V(t)=\bar{A}_{{35+t}}-\bar{P}(\bar{A}_{{35}})\bar{a}_{{35+t}}\mbox{ oraz }$

$V^{{\prime}}(t)=(\mu _{{35+t}}+\delta)\bar{A}_{{35+t}}-\mu _{{35+t}}-\bar{P}(\bar{A}_{{35}})[(\mu _{{35+t}}+\delta)\bar{a}_{{35+t}}-1].$

Na mocy założenia UDD mamy następujące wzory przybliżone

$\bar{A}_{{45}}=\frac{i}{\delta}\cdot\frac{M_{{45}}}{D_{{45}}}=?,\bar{a}_{{45}}=\frac{1-\bar{A}_{{45}}}{\delta}=?,\mu _{{45}}=q_{{45}}=0,008.$

Zatem $V(10)=?$ , $V^{{\prime}}(10)=?$ i stąd $\pi^{s}(10)=?$ .

5. Rozważamy rodzinę polis emerytalnych dla (x) parametryzowaną długością okresu płacenia składek $m>0$ . Dokładniej: polisa Pol(m) polega na tym, że przez najbliższe $m$ lat ubezpieczony (x) będzie płacił składkę netto w postaci renty życiowej $m$ -letniej ciągłej z odpowiednio dobraną stałą intensywnością netto; po dożyciu wieku $x+m$ zacznie otrzymywać emeryturę w postaci renty dożywotniej ciągłej z roczną intensywnością $1$ . Niech $0<t<m$ oraz niech $V(t)$ oznacza rezerwę składek netto po $t$ latach. Wykazać, że $\frac{\partial V(t)}{\partial m}$ wyraża się wzorem:

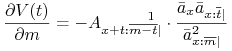$\frac{\partial V(t)}{\partial m}=-A_{{x+t:\overline{m-t}\mid}}^{{\ \ \ \ \ \ \ \ 1}}\cdot\frac{\bar{a}_{x}\bar{a}_{{x:\overline{t}\mid}}}{\bar{a}_{{x:\overline{m}\mid}}^{2}}$

Rozwiązanie. Z definicji rezerwy otrzymujemy jawny wzór na $V(t)$ ,

$V(t)=\mbox{}_{{m-t|}}\bar{a}_{{x+t}}-\bar{P}\bar{a}_{{x+t:\overline{m-t}\mid}}\mbox{ dla }0<t<m,$

gdzie

$\bar{P}=\frac{\mbox{}_{{m|}}\bar{a}_{x}}{\bar{a}_{{x:\overline{m}\mid}}}.$

Obliczamy odpowiednie pochodne

$\frac{\partial}{\partial m}(\mbox{}_{{m-t|}}\bar{a}_{{x+t}})=\frac{\partial}{\partial m}\int _{{m-t}}^{{\infty}}e^{{-\delta s}}\mbox{}_{s}p_{{x+t}}\, ds=-e^{{-\delta(m-t)}}\mbox{}_{{m-t}}p_{{x+t}},$

$\frac{\partial}{\partial m}(\bar{a}_{{x+t:\overline{m-t}\mid}})=\frac{\partial}{\partial m}\int _{0}^{{m-t}}e^{{-\delta s}}\mbox{}_{s}p_{{x+t}}\, ds=e^{{-\delta(m-t)}}\mbox{}_{{m-t}}p_{{x+t}},$

$\frac{\partial}{\partial m}(\mbox{}_{{m|}}\bar{a}_{x})=\frac{\partial}{\partial m}\int _{m}^{{\infty}}e^{{-\delta s}}\mbox{}_{s}p_{x}\, ds=-e^{{-\delta m}}\mbox{}_{m}p_{x},$

$\frac{\partial}{\partial m}(\bar{a}_{{x:\overline{m}\mid}})=e^{{-\delta m}}\mbox{}_{m}p_{x}.$

Dalej

$\frac{\partial V(t)}{\partial m}=-e^{{-\delta(m-t)}}\mbox{}_{{m-t}}p_{{x+t}}-\left[\frac{-e^{{-\delta m}}\mbox{}_{m}p_{x}\bar{a}_{{x:\overline{m}\mid}}-e^{{-\delta m}}\mbox{}_{m}p_{x}\mbox{}_{{m|}}\bar{a}_{x}}{\bar{a}^{2}_{{x:\overline{m}\mid}}}\right]\bar{a}_{{x+t:\overline{m-t}\mid}}-\bar{P}(m)e^{{-\delta(m-t)}}\mbox{}_{{m-t}}p_{{x+t}}=$

$-e^{{-\delta(m-t)}}\mbox{}_{{m-t}}p_{{x+t}}+\frac{e^{{-\delta m}}\mbox{}_{m}p_{x}\bar{a}_{x}\bar{a}_{{x+t:\overline{m-t}\mid}}}{\bar{a}^{2}_{{x:\overline{m}\mid}}}-\frac{e^{{-\delta(m-t)}}\mbox{}_{{m-t}}p_{{x+t}}\cdot\mbox{}_{{m|}}\bar{a}_{x}}{\bar{a}_{{x:\overline{m}\mid}}}=-\frac{e^{{-\delta(m-t)}}\mbox{}_{{m-t}}p_{{x+t}}\bar{a}_{x}}{\bar{a}_{{x:\overline{m}\mid}}}+$

$+\frac{e^{{-\delta m}}\mbox{}_{m}p_{x}\bar{a}_{x}\bar{a}_{{x+t:\overline{m-t}\mid}}}{\bar{a}^{2}_{{x:\overline{m}\mid}}}=-A_{{x+t:\overline{m-t}\mid}}^{{\ \ \ \ \ \ \ 1}}\left[\frac{\bar{a}_{x}\bar{a}_{{x:\overline{m}\mid}}-e^{{-\delta t}}\mbox{}_{t}p_{x}\bar{a}_{x}\bar{a}_{{x+t:\overline{m-t}\mid}}}{\bar{a}_{{x:\overline{m}\mid}}}\right]=-A_{{x+t:\overline{m-t}\mid}}^{{\ \ \ \ \ \ \ 1}}\cdot\frac{\bar{a}_{x}\bar{a}_{{x:\overline{t}\mid}}}{\bar{a}_{{x:\overline{m}\mid}}^{2}}.$

6. Rozważmy grupę $100$ osób w wieku (50). Każda z tych osób ubezpieczyła się kilka lub kilkanaście lat temu na życie i płaci regularne coroczne składki netto aż do śmierci (bieżący staż każdej z tych osób w ubezpieczeniu jest liczbą całkowitą). Obliczyć przeciętną liczbę polis, które nie przyniosą ubezpieczycielowi straty netto. Zakładamy, że wszystkie te osoby należą do tej samej populacji i że ich życia są niezależne. Można skorzystać z następujących danych:

$A_{{50}}=0,37,i=5\%,$

$l_{{30}}=96172,l_{{40}}=93348,l_{{50}}=86752,l_{{60}}=73602,l_{{70}}=51989,l_{{80}}=24644,l_{{90}}=4568.$

Rozwiązanie. Rozważmy jedną z osób z tej grupy ubezpieczonych. Jeśli ubezpieczyła się ona w wieku $x$ i $k$ lat temu to oczywiście $x+k=50$ . Strata ubezpieczyciela związana z tą polisą ma postać

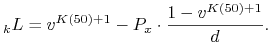$\mbox{}_{k}L=v^{{K(50)+1}}-P_{x}\cdot\frac{1-v^{{K(50)+1}}}{d}.$

Zdarzenie, że ta polisa nie przyniesie straty można zapisać nierównością

$\mbox{}_{k}L<\mbox{}_{k}V\mbox{ czyli }$

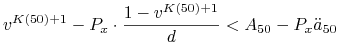$v^{{K(50)+1}}-P_{x}\cdot\frac{1-v^{{K(50)+1}}}{d}<A_{{50}}-P_{x}\ddot{a}_{{50}}$

która jest równoważna następującej

$v^{{K(50)+1}}<A_{{50}}$

i dalej

$K(50)+1>\frac{\ln A_{{50}}}{-\delta}=??\mbox{ czyli }K(50)\ge??$

Przeciętna liczba polis, które nie przyniosą straty wynosi więc ??.

7. Żona (20) jest wybrana z populacji de Moivre'a z wiekiem granicznym $100$ ; natomiast mąż (25) jest wybrany z populacji de Moivre'a z wiekiem granicznym $90$ . Rozpatrujemy następującą polisę emerytalną dla tej pary. Przez najbliższe $40$ lat będą płacić składki w postaci renty życiowej ciągłej, przy czym płacenie składek ustaje po pierwszej śmierci (jeśli ktoś umrze w ciągu najbliższych $40$ lat). Po $40$ latach zaczyna się wypłata emerytury w postaci renty życiowej ciągłej płacącej do drugiej śmierci z roczną intensywnością 1. Obliczyć intensywność $\bar{P}$ renty składek przyjmując techniczną intensywność oprocentowania na poziomie $\delta=0,02$ .

8. On (y) jest wylosowany z populacji Gompertza a ona (x) z populacji Weibulla. Dane są:

$e_{{x:y}}=7,\mu _{x}=0,02\mbox{ oraz }Pr(T(x)<T(y))=0,25.$

Obliczyć przybliżoną wartość

$e_{{x+\frac{1}{12}:y}}$

Rozwiązanie.Mamy

$e_{{x+\frac{1}{12}:y}}\approx e_{{x:y}}+\frac{1}{12}\frac{\partial}{\partial x}(e_{{x:y}}).$

Ale

$\frac{\partial}{\partial x}(e_{{x:y}})=\frac{\partial}{\partial x}\int _{0}^{{\infty}}\mbox{}_{t}p_{x}\cdot\mbox{}_{t}p_{y}\, dt=\int _{0}^{{\infty}}\mbox{}_{t}p_{y}\frac{\partial}{\partial x}(\mbox{}_{t}p_{x})\, dt=\int _{0}^{{\infty}}\mbox{}_{t}p_{y}[\mbox{}_{t}p_{x}(\mu _{x}-\mu _{{x+t}})]\, dt=$

$=\mu _{x}e_{{x:y}}-\int _{0}^{{\infty}}\mbox{}_{t}p_{x}\cdot\mbox{}_{t}p_{y}\mu _{{x+t}}\, dt=\mu _{x}e_{{x:y}}-Pr(T(x)<T(y)),$

więc ostatecznie

$e_{{x+\frac{1}{12}:y}}\approx 7+\frac{1}{12}(0,02\cdot 7-0,25)=6,9908.$

9. Rozważamy ubezpieczenie $30$ -letnie malejące dla (20) wybranego z populacji de Moivre'a z wiekiem granicznym $100$ . Suma ubezpieczenia $c(t)$ wypłacana jest w chwili śmierci i wynosi:

$c(t)=\left\{\begin{array}[]{ccc}(30-t+ft)/30&\mbox{dla}&t<30\\ 0&\mbox{dla}&t\ge 30.\end{array}\right.$

gdzie $f\in(0,1)$ jest parametrem. Składka opłacana jest w postaci renty życiowej ciągłej $30$ -letniej z odpowiednio dobraną intensywnością netto. Znaleźć najmniejsze $f$ , które spełnia warunek: dla każdego $t\in(0,30)$ zachodzi nierówność $V(t)\ge 0$ . Symbol $V(t)$ oznacza rezerwę składek netto po $t$ latach.

10. Rozważamy dwie populacje. Niech $g_{j}(x)$ oznacza gęstość rozkładu trwania życia noworodka wylosowanego z populacji $j$ ( $j=1,2$ .) Między funkcjami $g_{1}(x)$ oraz $g_{2}(x)$ zachodzi związek:

$g_{2}(x)=\left\{\begin{array}[]{ccc}0,9g_{1}(x)&\mbox{dla}&x<50\\ 1,1g_{1}(x)&\mbox{dla}&x>50.\end{array}\right.$

Niech dalej zmienna losowa $X_{j}$ oznacza długość życia noworodka wylosowanego z populacji $j$ . Udowodnić, że zachodzi wzór:

$E(min(X_{1},50))=5,5E(X_{1})-5E(X_{2})+25.$

11. Rozważamy dwie polisy bezterminowe na życie dla (x). Każda z nich wypłaca jako świadczenie $1$ zł na koniec roku śmierci. Polisa 1. opłacona jest za pomocą jednorazowej składki netto w momencie zawarcia umowy. Niech $L_{1}$ oznacza stratę ubezpieczyciela na moment wystawienia tej polisy. Natomiast w przypadku polisy 2. składki regularne netto będą płacone w postaci renty życiowej na początku każdego roku aż do śmierci. Niech $L_{2}$ oznacza stratę ubezpieczyciela na moment wystawienia tej polisy. Wiadomo, że

$\frac{Var(L_{2})}{Var(L_{1})}=1,826$

Obliczyć $A_{x}$ .

Rozwiązanie. Jak wiadomo

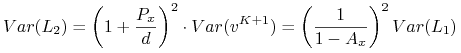$Var(L_{2})=\left(1+\frac{P_{x}}{d}\right)^{2}\cdot Var(v^{{K+1}})=\left(\frac{1}{1-A_{x}}\right)^{2}Var(L_{1})$

Obliczamy stąd $A_{x}=0,26.$

12. Rozważamy ubezpieczenie n-letnie na życie i dożycie ciągłe dla (x). Jeśli umrze on w ciągu najbliższych $n$ lat to zostanie wypłacone świadczenie $1$ zł w chwili śmierci, a jeżeli dożyje wieku $x+n$ to $1$ zł zostanie wypłacone właśnie w tym momencie. Składki netto będzie płacił w formie renty życiowej ciągłej $h$ -letniej, gdzie $0<h<n$ . Odpowiednią intensywność składki netto oznaczamy tradycyjnie symbolem $\mbox{}_{h}\bar{P}(\bar{A}_{{x:\overline{n}\mid}})$ . Załóżmy, że zwiększymy $n$ o jeden miesiąc. O ile należy zmniejszyć $h$ aby nie zmieniła się roczna intensywność składki netto. Dane są

$\mbox{}_{h}\bar{P}(\bar{A}_{{x:\overline{n}\mid}})=0,03,\ \ \ A_{{x+h:\overline{n-h}\mid}}^{{\ \ \ \ \ \ \ \ 1}}=0,55\mbox{ oraz }\delta=0,049.$

13. Rozważamy ubezpieczenie ciągłe dla (x), które wypłaci $t$ w chwili śmierci, jeśli ubezpieczony umrze w wieku (x+t). Niech $Z$ oznacza wartość obecną świadczenia na moment wystawienia polisy. Załóżmy, że ubezpieczony został wylosowany z populacji wykładniczej o średniej trwania życia $80$ . Techniczną intensywność oprocentowania $\delta$ wybrano na poziomie, który minimalizuje wartość współczynnika zmienności:

$\sqrt{Var(Z)})/E(Z)$

Obliczyć ten poziom $\delta$ .

14. Rozważamy polisę emerytalną, która polega na tym, że (x) płaci składki przez najbliższe $m$ lat w postaci renty życiowej ciągłej, a po dożyciu wieku $x+m$ zaczyna pobierać emeryturę z intensywnością $1$ na rok. W przypadku śmierci przed osiągnięciem wieku $x+m$ uposażeni otrzymują jednorazowe świadczenie w wysokości $\alpha$ razy suma wpłaconych dotychczas składek (w chwili śmierci). Niech $\bar{P}(\alpha)$ oznacza odpowiednią intensywność roczną składek netto. Wykazać, że zachodzi wzór:

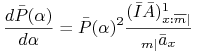$\frac{d\bar{P}(\alpha)}{d\alpha}=\bar{P}(\alpha)^{2}\frac{(\bar{I}\bar{A})_{{x:\overline{m}\mid}}^{1}}{\mbox{}_{{m|}}\bar{a}_{x}}$

Rozwiązanie. Intensywność składki obliczamy z równania

$E(P.V.(\mbox{składek }\bar{P}(\alpha)))=E(P.V.(\mbox{świadczeń})).$

W systuacji z zadania równanie to ma postać

$\bar{P}(\alpha)\cdot\bar{a}_{{x:\overline{m}\mid}}=1\cdot\mbox{}_{{m|}}\bar{a}_{x}+\alpha(\bar{I}\bar{A})^{1}_{{x:\overline{m}\mid}}\bar{P}(\alpha).$

Mamy stąd

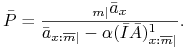$\bar{P}=\frac{\mbox{}_{{m|}}\bar{a}_{x}}{\bar{a}_{{x:\overline{m}\mid}}-\alpha(\bar{I}\bar{A})^{1}_{{x:\overline{m}\mid}}}.$

Otrzymujemy stąd natychmiast wzór na $\frac{d\bar{P}(\alpha)}{d\alpha}$ .

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Matematyka w ubezpieczeniach na życie

3. Zadania, I