4. Zadania,II

15. Rozważamy ubezpieczenie pary osób (x), (y), które wypłaca $T(x:y)$ zł w chwili pierwszej śmierci oraz $4T(\overline{x:y})$ zł w momencie drugiej śmierci. Zakładamy, że (x) jest wylosowany z populacji wykładniczej o średniej $100$ , natomiast (y) jest wylosowany z populacji wykładniczej o średniej $80$ . Obliczyć składkę jednorazową netto $SJN$ za to ubezpieczenie przyjmując techniczną intensywność oprocentowania na poziomie $\delta=0,02$ . Zakładamy, że zmienne losowe $T(x)$ oraz $T(y)$ są niezależne.

Rozwiązanie. Szukana składka $SJN$ wynosi

$SJN=(\bar{I}\bar{A})_{{x:y}}+4(\bar{I}\bar{A})_{{\overline{x:y}}}.$

Ponieważ

$(\bar{I}\bar{A})_{x}+(\bar{I}\bar{A})_{y}=(\bar{I}\bar{A})_{{x:y}}+(\bar{I}\bar{A})_{{\overline{x:y}}}$

więc

$SJN=4(\bar{I}\bar{A})_{x}+4(\bar{I}\bar{A})_{y}-3(\bar{I}\bar{A})_{{x:y}}.$

Obliczamy potrzebne symbole

$(\bar{I}\bar{A})_{x}=\int _{0}^{{\infty}}te^{{-0,02t}}e^{{-0,01t}}0,01\, dt=11,1111$

$(\bar{I}\bar{A})_{y}=\int _{0}^{{\infty}}te^{{-0,02t}}e^{{-0,0125t}}0,0125\, dt=11,8343$

$(\bar{I}\bar{A})_{{x:y}}=\int _{0}^{{\infty}}te^{{-0,02t}}e^{{-0,0225t}}0,0225\, dt=12,4567.$

Ostatecznie otrzymujemy $SJN=54,4115$ .

16. Rozpatrujemy model szkodowości dwojakiej:

$\mu _{{1,x+t}}=\frac{1}{100-t},\ \ \ \mu _{{2,x+t}}=\frac{2}{120-t}\mbox{ dla }0\le t<100.$

Obliczyć prawdopodobieństwo zdarzenia, że (x) ulegnie jako pierwszej szkodzie tej, która w danej chwili mniej mu zagrażała niż druga ”współzawodnicząca”.

Rozwiązanie. Rozwiązujemy najpierw równanie

$\mu _{{1,x+t}}=\mu _{{2,x+t}}$

i otrzymujemy $t=80.$ Zatem dla $t<80$ bardziej zagraża mu szkoda druga ( $J=2$ ) a dla $t>80$ szkoda pierwsza ( $J=1$ .) Szukane prawdopodobieństwo wynosi więc

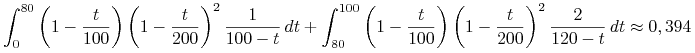$\int _{0}^{{80}}\left(1-\frac{t}{100}\right)\left(1-\frac{t}{200}\right)^{2}\frac{1}{100-t}\, dt+\int _{{80}}^{{100}}\left(1-\frac{t}{100}\right)\left(1-\frac{t}{200}\right)^{2}\frac{2}{120-t}\, dt\approx 0,394$

17. Rozważamy grupę $10$ osób w wiekach $21,22,23,24,25,26,27,28,29,30$ . Zakładamy, że ich życia są niezależne oraz, że wszystkie te osoby pochodzą z populacji Gompertza z funkcją natężenia śmiertelności daną wzorem:

$\mu _{x}=B(1,23)^{x}$

gdzie $B>0$ . Jakie jest prawdopodobieństwo zdarzenia, że jako pierwszy umrze parzystolatek?

Rozwiązanie. Niech $n=21:23:\ldots:29$ oraz $p=22:24:\ldots:30$ . Mamy obliczyć prawdopodobieństwo, że $T(p)<T(n)$ . Niech dalej $c=1,23.$ Mamy

$\mu _{{n+t}}=Bc^{{21+t}}+Bc^{{23+t}}+\ldots+Bc^{{29+t}}=Bc^{{w_{n}+t}}$

gdzie $w_{n}$ spełnia równanie

$c^{{w_{n}}}=c^{{21}}+c^{{23}}+\cdots c^{{29}}.$

Podobnie

$\mu _{{p+t}}=Bc^{{w_{p}+t}}$

gdzie $w_{p}$ spełnia równanie

$c^{{w_{p}}}=c^{{22}}+c^{{24}}+\cdots c^{{30}}.$

Zatem

$w_{p}=w_{n}+1$

i dalej

$Pr(T(p)<T(n))=\int _{0}^{{\infty}}\mbox{}_{t}p_{n}\cdot\mbox{}_{t}p_{p}\cdot\mu _{{p+t}}=\int _{0}^{{\infty}}\mbox{}_{t}p_{{w_{n}}}\cdot\mbox{}_{t}p_{{w_{p}}}(\mu _{{w_{p}+t}}+\mu _{{w_{n}+t}})\frac{\mu _{{w_{p}+t}}}{\mu _{{w_{p}+t}}+\mu _{{w_{n}+t}}}=$

$=\frac{c^{{w_{p}}}}{c^{{w_{p}}}+c^{{w_{n}}}}\cdot 1=\frac{c}{c+1}\approx 0,55.$

18. Rozważamy ubezpieczenie $n$ -letnie na życie dla (x), ciągłe, które wypłaci $1$ zł w chwili śmierci, jeżeli ubezpieczony umrze w ciągu $n$ lat. Składki są płacone w postaci renty życiowej ciągłej $n$ -letniej z odpowiednio dobraną stałą intensywnością netto $\bar{P}$ . Niech $W(t)=e^{{-\delta t}}\bar{V}(t)$ oznacza wartość obecną rezerwy po $t$ latach, obliczoną na moment wystawienia polisy. Załóżmy, że funkcja $W(t)$ osiąga maksimum w pewnym punkcie $t^{{\ast}}\in(0,n)$ . Obliczyć $\bar{P}$ , jeśli wiadomo, że

$\bar{V}(t^{{\ast}})=0,1\mbox{ oraz }\mu _{{x+t^{{\ast}}}}=0,01.$

Rozwiązanie. Ponieważ

$W^{{\prime}}(t)=-\delta e^{{-\delta t}}V(t)+e^{{-\delta t}}V^{{\prime}}(t)=e^{{-\delta t}}[V^{{\prime}}(t)-\delta V(t)]$

więc $t^{{\ast}}$ spełnia równanie

$V^{{\prime}}(t^{{\ast}})-\delta V(t^{{\ast}})=0.$

Uwzględniając równanie Thielego otrzymujemy stąd

$\bar{P}=(1-V(t^{{\ast}}))\mu _{{x+t^{{\ast}}}}=0,009.$

19. Rozważamy ubezpieczenie emerytalne dla (x), wybranego z populacji de Moivre'a z wiekiem granicznym $\omega>x$ . Polega ono na tym, że przez najbliższe $m$ lat ( $m<\omega-x$ ), będzie on płacił składkę w postaci renty życiowej ciągłej z intensywnością netto $1$ . Po dożyciu wieku $x+m$ zacznie otrzymywać emeryturę dożywotnią z intensywnością $E$ . Do rachunków netto użyto technicznej intensywności oprocentowania $\delta=0$ . Intensywność emerytury $E$ jest więc funkcją $x,m$ oraz $\omega$ . Udowodnić, że elastyczność $E$ względem wieku granicznego $\omega$ wyraża się wzorem:

$\frac{\partial E}{\partial\omega}\cdot\frac{\omega}{E}=\frac{2\omega(x-\omega)}{(\omega-x-m)(2\omega-2x-m)}$

20. Niech $\stackrel{\circ}{e}_{x}=E(T(x))=\frac{(100-x)(175-x)}{3(150-x)}$ (dla $0\le x<100$ ) oznacza przeciętne dalsze trwanie życia (x) wylosowanego z populacji z wiekiem nieprzekraczalnym $100$ . Obliczyć

$\mbox{}_{{24}}p_{{46}}$

Rozwiązanie. Łatwo sprawdzić, że funkcja $\stackrel{\circ}{e}_{x}$ spełnia równanie różniczkowe

$\stackrel{\circ}{e}_{x}^{{\prime}}=\mu _{x}\stackrel{\circ}{e}_{x}-1$

(porównaj z równaniem różniczkowym na $\bar{a}_{x}$ !) więc

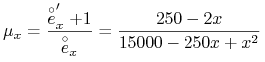$\mu _{x}=\frac{\stackrel{\circ}{e}_{x}^{{\prime}}+1}{\stackrel{\circ}{e}_{x}}=\frac{250-2x}{15000-250x+x^{2}}$

Otrzymujemy stąd, że

$[\ln s(x)]^{{\prime}}=[\ln(x^{2}-250x+15000)]^{{\prime}}$

i uwzględniając warunek początkowy $s(0)=1$ dostajemy

$s(x)=\frac{(100-x)(150-x)}{15000}\mbox{ dla }0<x<100.$

W szczególności

$\mbox{}_{{24}}p_{{46}}=\frac{s(70}{s(46)}=\frac{50}{117}\approx 0,427$

21. Rozważamy wyjściowy symbol $A_{{x:\overline{m}\mid}}^{{\ \ \ 1}}$ oznaczający składkę jednorazową netto za $m$ -letnie ubezpieczenie na dożycie dla (x). Załóżmy, że małe liczby $\Delta x$ oraz $\Delta m$ zostały tak dobrane, że

$A_{{x+\Delta x:\overline{m+\Delta m}\mid}}^{{\ \ \ \ \ \ \ \ \ \ \ \ 1}}=A_{{x:\overline{m}\mid}}^{{\ \ \ 1}}.$

Obliczyć wartość przybliżoną $\Delta m/\Delta x$ .

Dane są:

$\delta=0.03,\mu _{x}=0,01,\mu _{{x+m}}=0,015.$

22. Rozważamy populację wykładniczą z natężeniem umierania:

$\mu _{x}=const=\mu>0.$

Wybrany z niej (x) kupuje ubezpieczenie ciągłe na życie odroczone o $m>0$ lat. Płaci do końca życia ciągłą rentę życiową składek netto z odpowiednio dobraną stałą intensywnością $\bar{P}$ . Jeśli umrze w ciągu najbliższych $m$ lat to żadne świadczenie nie będzie wypłacone. Natomiast, gdy umrze później to zostanie wypłacone $1$ zł w chwili jego śmierci. Niech $\delta>0$ oznacza poziom technicznej intensywności oprocentowania użytej do obliczenia składek i rezerw. Wykazać, że intensywność składki oszczędnościowej po $2m$ latach $\pi^{s}(2m)$ wyraża się wzorem:

$\pi^{s}(2m)=-\frac{\mu\delta}{\mu+\delta}(1-e^{{-m(\mu+\delta)}}).$

Rozwiązanie. Ponieważ

$\bar{a}_{x}=\int _{0}^{{\infty}}e^{{-\delta t}}e^{{-\mu t}}\, dt=\frac{1}{\mu+\delta}$

oraz

$\mbox{}_{{m|}}\bar{A}_{x}=v^{m}e^{{-\mu m}}\bar{A}_{{x+m}}=e^{{-(\mu+\delta)m}}\frac{\mu}{\mu+\delta}$

więc

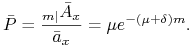$\bar{P}=\frac{\mbox{}_{{m|}}\bar{A}_{x}}{\bar{a}_{x}}=\mu e^{{-(\mu+\delta)m}}.$

Dla $t>m$ mamy

$V(t)=\bar{A}_{{x+t}}-\bar{P}\bar{a}_{{x+t}}=const\mbox{ a zatem }V^{{\prime}}(t)=0.$

W szczególności

$\pi^{s}(2m)=V^{{\prime}}(2m)-\delta V(2m)=-\delta\left(\frac{\mu}{\mu+\delta}-\mu e^{{-(\mu+\delta)m}}\frac{1}{\mu+\delta}\right)$

czego należało dowieść.

23. Rozważamy ubezpieczenie ciągłe ogólnego typu, które ma tę własność, że dla każdego $t>0$ zachodzi równość

$\pi^{s}(t)=\pi^{r}(t).$

Po lewej stronie mamy intensywność składki oszczędnościowej a po prawej stronie mamy intensywność składki na ryzyko. Wykazać, że bieżące poziomy: rezerwy $V(t)$ , świadczenia śmiertelnego $c(t)$ oraz intensywności składki netto $\pi(t)$ powiązane są zależnością:

$V(t)=c(t)-\frac{\pi(t)}{2\mu _{{x+t}}}$

Rozwiązanie. Z treści zadania mamy

$V^{{\prime}}(t)-\delta V(t)=\mu _{{x+t}}(c(t)-V(t))$

Równanie Thielego głosi natomiast, że

$V^{{\prime}}(t)=\delta V(t)+\pi(t)-(c(t)-V(t))\mu _{{x+t}}$

Jeśli z powyższych równań wyrugujemy $V^{{\prime}}(t)$ i otrzymane równanie rozwiążemy ze względu na $V(t)$ to dostaniemy pożądany wzór.

24. Rozważamy ubezpieczenie bezterminowe na życie ciągłe dla (30), wybranego z populacji de Moivre'a z wiekiem granicznym $\omega=110$ . Wypłaci ono $1$ zł w chwili jego śmierci. Składka jednorazowa $SJ$ , którą zapłaci ubezpieczony w momencie zawarcia umowy ubezpieczeniowej, została skalkulowana jako wartość oczekiwana wartości obecnej wypłaty pod warunkiem, że ubezpieczony umrze wcześniej niż przeciętnie. Obliczyć prawdopodobieństwo:

$Pr(v^{{T(30)}}<SJ).$

W powyższym wzorze $v$ oznacza techniczny roczny czynnik dyskontujący, odpowiadający technicznej intensywności oprocentowania $\delta=0,02$ .

25. Rozważamy ubezpieczenie bezterminowe dla (x), które wypłaci $1$ zł na koniec roku śmierci. Składki opłacane są za pomocą renty życiowej składek corocznych w stałej wysokości netto $P_{x}$ . Wiadomo, że dla pewnego całkowitego $k>0$ zachodzi:

$\mbox{}_{k}V=0,60,\ \ \mbox{}_{{k+2}}V=0,64,\ \ p_{{x+k}}=0,92,\ \ p_{{x+k+1}}=0,88,\ \ i=4\%.$

Obliczyć $P_{x}$ .

26. Mąż (30) należy do populacji de Moivre'a z wiekiem granicznym $\omega _{m}=100$ , natomiast żona (25) należy do populacji de Moivre'a z wiekiem granicznym $\omega _{k}=120$ . Rozpatrujemy ubezpieczenie bezterminowe ciągłe dla tej pary, które wypłaci $1$ zł w chwili pierwszej śmierci. Składka za to ubezpieczenie będzie płacona aż do pierwszej śmierci za pomocą renty życiowej ciągłej z odpowiednio dobraną intensywnością netto $\bar{P}$ . Obliczyć rezerwę składek netto $V(50)$ po $50$ latach od momentu wystawienia polisy. Techniczna intensywność oprocentowania wynosi $\delta=0,05$ . Zakładamy ponadto, że $T(30)$ oraz $T(25)$ są niezależne.

Rozwiązanie. Intensywność $\bar{P}$ składki netto spełnia bilans aktuarialny

$\bar{P}\bar{a}_{{30:25}}=\bar{A}_{{30:25}}=1-\delta\bar{a}_{{30:25}}\mbox{ a zatem }\bar{P}=\bar{a}^{{-1}}_{{30:25}}-\delta.$

Obliczamy potrzebny symbol rentowy

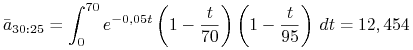$\bar{a}_{{30:25}}=\int _{0}^{{70}}e^{{-0,05t}}\left(1-\frac{t}{70}\right)\left(1-\frac{t}{95}\right)\, dt=12,454$

Otrzymujemy więc $\bar{P}=0,0302958$ . Dalej

$V(50)=\bar{A}_{{80:75}}-\bar{P}\bar{a}_{{80:75}}=1-(\delta+\bar{P})\bar{a}_{{80:75}}=0,483188.$

27. (x) wybrano z populacji de Moivre'a z wiekiem granicznym $\omega>0$ . Natomiast (y) wybrano niezależnie z populacji wykładniczej z funkcją natężenia wymierania $\mu _{{y+t}}=const=\mu>0$ . Wybrane osoby mają przed sobą przeciętnie tyle samo życia. Obliczyć prawdopodobieństwo zdarzenia, że

$T(x)>T(y).$

Zakładamy, że $T(x)$ oraz $T(y)$ są niezależne.

Rozwiązanie. Mamy

$T(x)\sim{\rm U}(0,\omega-x)\mbox{ gdzie }0<x<\omega$

oraz

$T(y)\sim{\rm Exp}(\mu)\mbox{ gdzie }\mu>0.$

Z treści zadania mamy

$E(T(x))=E(T(y))\mbox{ tzn. }$

$\frac{\omega-x}{2}=\frac{1}{\mu}.$

Obliczamy szukane prawdopodobieństwo

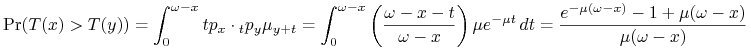$\Pr(T(x)>T(y))=\int _{0}^{{\omega-x}}\mbox{}tp_{x}\cdot\mbox{}_{t}p_{y}\mu _{{y+t}}=\int _{0}^{{\omega-x}}\left(\frac{\omega-x-t}{\omega-x}\right)\mu e^{{-\mu t}}\, dt=\frac{e^{{-\mu(\omega-x)}}-1+\mu(\omega-x)}{\mu(\omega-x)}$

Uwzględniając powyższą zależność pomiędzy $\omega,x$ oraz $\mu$ otrzymujemy ostatecznie

$\Pr(T(x)>T(y))=\frac{1}{2}(1+e^{{-2}})\approx 0,5677.$

28. Rozważamy model dwuopcyjny (multiple decrement model), przy czym

$\mu _{{1,x+t}}=\frac{1}{\omega _{1}-t}\mbox{ dla }0<t<\omega _{1}\mbox{ oraz }\mu _{{2,x+t}}=\frac{1}{\omega _{2}-t}\mbox{ dla }0<t<\omega _{2},$

przy czym zakładamy, że $\omega _{1}<\omega _{2}$ . Obliczyć stosunek $\omega _{1}/\omega _{2}$ dla którego największe jest prawdopodobieństwo

$Pr(T>E(T)|J=1).$

29. Rozważamy ubezpieczenie emerytalne dla (25). Polega ono na tym, że w ciągu najbliższych $35$ lat będzie on płacił regularną coroczną składkę netto w wysokości $P$ . Po dożyciu wieku $60$ lat zacznie on otrzymywać emeryturę dożywotnią w wysokości $1$ zł na początku każdego roku. Niech $L$ oznacza wartość obecną straty ubezpieczyciela na moment wystawienia polisy. Obliczyć $Var(L)$ . Dane są:

$i=6\%,\mbox{}_{{35}}p_{{25}}=0,856044,\ \ A_{{25}}=0,0816496,\ A_{{60}}=0,3691310,\ \mbox{}^{2}A_{{25}}=0,0187472,\ \mbox{}^{2}A_{{60}}=0,1774113.$

30. Niech $m(x)$ oznacza medianę dalszego trwania życia (x) tzn. medianę zmiennej losowej $T(x)$ . Dana jest funkcja natężenia umierania :

$\mu _{x}=0,01\cdot 1,02^{x}\mbox{ dla }x>0.$

Obliczyć $m(33)$ .

31. Rozważamy grupę 100 noworodków wybranych z populacji de Moivre'a z wiekiem granicznym $\omega=100$ . Obliczyć wariancję czasu oczekiwania do pierwszej śmierci w grupie. Zakładamy, że ich życia są niezależne.

Rozwiązanie. Mamy obliczyć wariancję zmiennej losowej $T(u)$ gdzie $u=x_{1}:x_{2}:\ldots:x_{{100}}$ oraz $x_{1}=x_{2}=\ldots=x_{{100}}=0$ . Ponieważ $T(u)=\min _{{j}}T(x_{j})$ więc

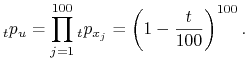$\mbox{}_{t}p_{u}=\prod _{{j=1}}^{{100}}\mbox{}_{t}p_{{x_{j}}}=\left(1-\frac{t}{100}\right)^{{100}}.$

Mamy teraz

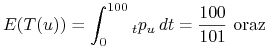$E(T(u))=\int _{0}^{{100}}\mbox{}_{t}p_{u}\, dt=\frac{100}{101}\mbox{ oraz }$

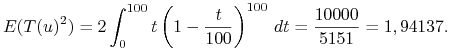$E(T(u)^{2})=2\int _{0}^{{100}}t\left(1-\frac{t}{100}\right)^{{100}}\, dt=\frac{10000}{5151}=1,94137.$

Ostatecznie $Var(T(u))=0,961075$

32. Rozważamy zmianę śmiertelności w wyjściowej populacji zadaną wzorem:

$\mu _{{x+t}}^{{(M)}}=\mu _{{x+t}}+M,$

dla wszystkich $x,t\ge 0$ . Zakładamy, że nieznany współczynnik przesunięcia $M$ ma rozkład jednostajny na odcinku $[0,01;0,02]$ . Wiadomo, że dla wyjściowej populacji

$A_{{x:\overline{35}\mid}}^{{\ \ \ 1}}=0,195276.$

Obliczyć wartość oczekiwaną składki $A_{{x:\overline{35}\mid}}^{{\ \ \ 1}}$ względem rozkładu zmiennej $M$ .

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Matematyka w ubezpieczeniach na życie

4. Zadania,II