5. Zadania,III
33. Za składkę jednorazową netto (x) kupuje rentę życiową ciągłą, która przez najbliższe ![]() lat będzie mu wypłacać z intensywnością
lat będzie mu wypłacać z intensywnością ![]() na rok, a po dożyciu wieku (x+n) z intensywnością
na rok, a po dożyciu wieku (x+n) z intensywnością ![]() na rok, aż do śmierci. Niech
na rok, aż do śmierci. Niech ![]() oznacza wartość obecną tych świadczeń emerytalnych na moment wystawienia polisy.
Dane są:
oznacza wartość obecną tych świadczeń emerytalnych na moment wystawienia polisy.
Dane są:
Wykazać, że:
34. Niech ![]() oznacza regularną składkę netto, którą będzie płacić ubezpieczony (x) na początku każdego roku aż do śmierci za ubezpieczenie rosnące, które wypłaci uposażonym
oznacza regularną składkę netto, którą będzie płacić ubezpieczony (x) na początku każdego roku aż do śmierci za ubezpieczenie rosnące, które wypłaci uposażonym ![]() , jeżeli umrze on w
, jeżeli umrze on w ![]() roku ważności polisy. Udowodnić wzór:
roku ważności polisy. Udowodnić wzór:
Rozwiązanie. Z wzoru
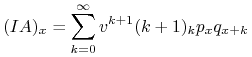 |
łatwo uzyskujemy zależność rekurencyjną
Mamy zatem
skąd wynika teza.
35. Rozważamy kontrakt ubezpieczeniowy ciągły ogólnego typu dla osoby w wieku (x). Wiadomo, że dla każdego ![]() mamy zależność:
mamy zależność:
gdzie ![]() jest stałą dodatnią. Techniczna intensywność oprocentowania wynosi
jest stałą dodatnią. Techniczna intensywność oprocentowania wynosi ![]() . Wykazać, że rezerwa składek netto
. Wykazać, że rezerwa składek netto ![]() po
po ![]() latach wynosi:
latach wynosi:
36. Ubezpieczenie emerytalne dla (x), wziętego z populacji o wykładniczym rozkładzie trwania życia:
polega na tym, że przez najbliższe ![]() lat będzie płacił coroczną regularną składkę w odpowiednio dobranej wysokości netto
lat będzie płacił coroczną regularną składkę w odpowiednio dobranej wysokości netto ![]() a po dożyciu wieku
a po dożyciu wieku ![]() zacznie otrzymywać emeryturę dożywotnią w wysokości
zacznie otrzymywać emeryturę dożywotnią w wysokości ![]() na początku roku. Obliczyć
na początku roku. Obliczyć
![]() .
Techniczna stopa oprocentowania użyta do obliczenia składki i rezerw wynosi
.
Techniczna stopa oprocentowania użyta do obliczenia składki i rezerw wynosi ![]() .
(zakładamy, że obie liczby
.
(zakładamy, że obie liczby ![]() oraz
oraz ![]() są całkowite dodatnie).
są całkowite dodatnie).
37. Mąż (30) należy do populacji de Moivre'a z wiekiem granicznym ![]() , natomiast żona (25) należy do populacji de Moivre'a z wiekiem granicznym
, natomiast żona (25) należy do populacji de Moivre'a z wiekiem granicznym ![]() . Obliczyć średni czas przebywania we wdowieństwie owdowiałej osoby. Zakładamy, że
. Obliczyć średni czas przebywania we wdowieństwie owdowiałej osoby. Zakładamy, że ![]() oraz
oraz ![]() są niezależne oraz, że owdowiała osoba nie wstępuje w związek małżeński.
są niezależne oraz, że owdowiała osoba nie wstępuje w związek małżeński.
38. Rozpatrujemy rentę wdowią dla niej (x) i dla niego (y):
-
(a) w przypadku, gdy ona umrze jako pierwsza on zacznie otrzymywać rentę dożywotnią ciągłą z intensywnością
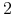 na rok (począwszy od jej śmierci);
na rok (począwszy od jej śmierci); -
(b) natomiast, gdy on umrze jako pierwszy ona zacznie otrzymywać rentę dożywotnią ciągłą z intensywnością
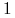 na rok (począwszy od jego śmierci).
na rok (począwszy od jego śmierci).
Niech ![]() oznacza wartość obecną świadczeń z tej polisy na moment jej wystawienia.
Obliczyć prawdopodobieństwo zdarzenia, że ona umrze jako pierwsza pod warunkiem, że
oznacza wartość obecną świadczeń z tej polisy na moment jej wystawienia.
Obliczyć prawdopodobieństwo zdarzenia, że ona umrze jako pierwsza pod warunkiem, że ![]() .
Wiadomo, że:
.
Wiadomo, że:
Zakładamy, że ![]() oraz
oraz ![]() są niezależne.
są niezależne.
39. Rozważamy polisę ciągłą ogólnego typu wystawioną osobie w wieku ![]() wybranej z populacji de Moivre'a z wiekiem granicznym
wybranej z populacji de Moivre'a z wiekiem granicznym ![]() , gdzie
, gdzie ![]() . Gdy ubezpieczony umrze w wieku
. Gdy ubezpieczony umrze w wieku ![]() będzie wypłacone świadczenie w wysokości
będzie wypłacone świadczenie w wysokości ![]() .
Wiadomo ponadto, że rezerwy składek netto po czasie
.
Wiadomo ponadto, że rezerwy składek netto po czasie ![]() wynoszą:
wynoszą:
Obliczyć
Zakładamy, że techniczna intensywność oprocentowania ![]() spełnia warunek
spełnia warunek
![]() .
Wybrać odpowiedź najbliższą.
.
Wybrać odpowiedź najbliższą.
40. Osoba w wieku (30) zaczyna płacić składki regularne w wysokości netto ![]() na początku każdego roku, aż do śmierci. Na koniec roku śmierci uposażeni otrzymają sumę ubezpieczenia równą
na początku każdego roku, aż do śmierci. Na koniec roku śmierci uposażeni otrzymają sumę ubezpieczenia równą ![]() . Załóżmy, że po
. Załóżmy, że po ![]() latach ubezpieczony żyje i niech
latach ubezpieczony żyje i niech
![]() oznacza stratę ubezpieczyciela na ten moment. Obliczyć
oznacza stratę ubezpieczyciela na ten moment. Obliczyć
Dane są:
41. Niech ![]() będzie liczbą całkowitą nieujemną oraz
będzie liczbą całkowitą nieujemną oraz ![]() . Niech ponadto
. Niech ponadto ![]() oznacza
oznacza ![]() obliczone przy założeniu UDD, natomiast
obliczone przy założeniu UDD, natomiast ![]() niech oznacza
niech oznacza ![]() obliczone przy założeniu Balducciego.
Udowodnić wzór:
obliczone przy założeniu Balducciego.
Udowodnić wzór:
42. Niech
oraz podobnie niech
Wyprowadzić następujący wzór przybliżony:
43. Niech ![]() oznacza wartość obecną renty życiowej dla (x), która wypłaca
oznacza wartość obecną renty życiowej dla (x), która wypłaca ![]() zł na początku roku, co rok, aż do śmierci, obliczoną przy technicznej intensywności oprocentowania
zł na początku roku, co rok, aż do śmierci, obliczoną przy technicznej intensywności oprocentowania ![]() . Podobnie niech
. Podobnie niech ![]() oznacza wartość obecną tego samego strumienia płatności, ale obliczoną przy intensywności oprocentowania
oznacza wartość obecną tego samego strumienia płatności, ale obliczoną przy intensywności oprocentowania ![]() . Oto realizacje zmiennych
. Oto realizacje zmiennych ![]() oraz
oraz ![]() :
:
Obliczyć realizację zmiennej ![]() .
.
44. Wykazać, że roczna intensywność składki ![]() spełnia następujące równanie różniczkowe:
spełnia następujące równanie różniczkowe:
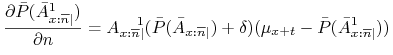 |
45. W rozważanej populacji śmiertelnością rządzi prawo Weibulla:
Rozpatrujemy ubezpieczenie ciągłe ![]() -letnie ogólnego typu dla (0), które będzie opłacane za pomocą ciągłej renty życiowej składek netto ze stałą roczną intensywnością:
-letnie ogólnego typu dla (0), które będzie opłacane za pomocą ciągłej renty życiowej składek netto ze stałą roczną intensywnością:
Natomiast wysokość świadczenia śmiertelnego ![]() związana jest z poziomem rezerwy netto
związana jest z poziomem rezerwy netto ![]() wzorem:
wzorem:
Techniczna intensywność oprocentowania wynosi ![]() .
Udowodnić, że
.
Udowodnić, że ![]() oraz
oraz ![]() powiązane są zależnością:
powiązane są zależnością:
46. Rozważamy demografię Weibulla z funkcją natężenia wymierania
gdzie ![]() jest parametrem. Rozważmy ubezpieczenie ciągłe ogólnego typu dla (x).
Wiadomo, że dla
jest parametrem. Rozważmy ubezpieczenie ciągłe ogólnego typu dla (x).
Wiadomo, że dla ![]() mamy
mamy
przy czym ![]() . Dane są ponadto:
. Dane są ponadto:
Obliczyć ![]() .
.
47. Za składkę jednorazową brutto ![]() osoba w wieku (65) kupuje ubezpieczenie emerytalne typu Emer(n), które działa w następujący sposób:
osoba w wieku (65) kupuje ubezpieczenie emerytalne typu Emer(n), które działa w następujący sposób:
-
wypłacana jest emerytura dożywotnia w postaci renty życiowej ciągłej ze stałą roczną intensywnością
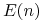 ,
, -
ponadto jeśli ubezpieczony umrze w wieku
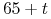 gdzie
gdzie 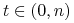 to wyznaczeni uposażeni otrzymają natychmiast jednorazowe świadczenie w wysokości
to wyznaczeni uposażeni otrzymają natychmiast jednorazowe świadczenie w wysokości 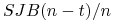 .
.
Parametr ![]() może być wybrany z przedziału
może być wybrany z przedziału ![]() w momencie zakupu polisy. Składka jednorazowa netto
w momencie zakupu polisy. Składka jednorazowa netto ![]() jest o
jest o ![]() mniejsza od składki brutto
mniejsza od składki brutto ![]() .
Udowodnić wzór:
.
Udowodnić wzór:
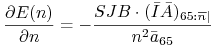 |
48. Ubezpieczenie dla grupy ![]() osób działa w ten sposób, że w momencie każdej śmierci wypłaca się po
osób działa w ten sposób, że w momencie każdej śmierci wypłaca się po ![]() zł każdej osobie przeżywającej (tak więc np. w momencie pierwszej śmierci w grupie ubezpieczyciel wypłaca
zł każdej osobie przeżywającej (tak więc np. w momencie pierwszej śmierci w grupie ubezpieczyciel wypłaca ![]() zł, a w momencie przedostatniej wypłaca
zł, a w momencie przedostatniej wypłaca ![]() zł). Zakładamy, że jednoczesna śmierć dwóch lub więcej osób nie jest możliwa i że ich życia są niezależne.
Cztery spośród tych osób należą do populacji wykładniczej ze średnią trwania życia
zł). Zakładamy, że jednoczesna śmierć dwóch lub więcej osób nie jest możliwa i że ich życia są niezależne.
Cztery spośród tych osób należą do populacji wykładniczej ze średnią trwania życia ![]() . Pozostałe trzy osoby należą do populacji wykładniczej ze średnią trwania życia
. Pozostałe trzy osoby należą do populacji wykładniczej ze średnią trwania życia ![]() . Przyjmując techniczną intensywność oprocentowania na poziomie
. Przyjmując techniczną intensywność oprocentowania na poziomie ![]() obliczyć składkę jednorazową netto
obliczyć składkę jednorazową netto ![]() za to ubezpieczenie.
za to ubezpieczenie.
Rozwiązanie. Łatwo widzieć, że
(porównaj z przykładem 6, str. 136,Sk). Rozpatrujemy trzy przypadki.
-
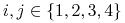 . Wówczas
. Wówczas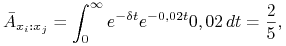
-
gdy
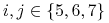 to podobnie obliczamy
to podobnie obliczamy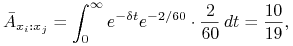
-
gdy
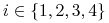 ,
, 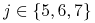 to
to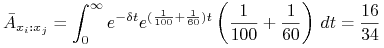
Ostatecznie więc
49. Rozważamy emeryturę małżeńską dla męża (65) i żony (60), przy czym on jest wylosowany z populacji de Moivre'a z wiekiem granicznym ![]() a ona jest wybrana z populacji de Moivre'a z wiekiem granicznym
a ona jest wybrana z populacji de Moivre'a z wiekiem granicznym ![]() . Emeryturę będą otrzymywać w formie renty życiowej ciągłej. Póki żyją oboje roczna intensywność renty wynosi
. Emeryturę będą otrzymywać w formie renty życiowej ciągłej. Póki żyją oboje roczna intensywność renty wynosi ![]() zł; po pierwszej śmierci intensywność emerytury dla owdowiałej osoby wynosi
zł; po pierwszej śmierci intensywność emerytury dla owdowiałej osoby wynosi ![]() zł.
Techniczna intensywność oprocentowania wynosi
zł.
Techniczna intensywność oprocentowania wynosi ![]() .
Obliczyć składkę jednorazową netto
.
Obliczyć składkę jednorazową netto ![]() .
.
Rozwiązanie. Mamy
Przede wszystkim
Dalej
![\bar{a}_{{60:65}}=E(\min(T(60),T(65)))=\frac{1}{60\cdot 40}\left[\int _{0}^{{40}}\left(\int _{x}^{{40}}x\, dy\right)\, dx+\int _{0}^{{40}}\left(\int _{y}^{{60}}y\, dx\right)\, dy\right]=\frac{140}{9}](wyklady/muz/mi/mi330.png) |
Ostatecznie
50. ![]() -latek , wylosowany z populacji de Moivre'a z wiekiem granicznym
-latek , wylosowany z populacji de Moivre'a z wiekiem granicznym ![]() , zaczyna odkładać na przyszłą emeryturę z intensywnością
, zaczyna odkładać na przyszłą emeryturę z intensywnością ![]() na rok w formie renty życiowej ciągłej. Emeryturę zacznie pobierać w wieku
na rok w formie renty życiowej ciągłej. Emeryturę zacznie pobierać w wieku ![]() , również z intensywnością
, również z intensywnością ![]() , aż do śmierci (o ile dożyje wieku
, aż do śmierci (o ile dożyje wieku ![]() ). Z aktuarialnej zasady równoważności (netto) wyprowadzić następujące równanie na
). Z aktuarialnej zasady równoważności (netto) wyprowadzić następujące równanie na ![]() :
:
Odpowiedzi do zadań rachunkowych.
2. ![]()
4. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
11. ![]()
12. ![]() miesiąca
miesiąca
13. ![]()
15. ![]() zł
zł
16. ![]()
17. ![]()
18. ![]()
20. ![]()
21. ![]()
24.
![]()
25. ![]() gr
gr
26. ![]() zł
zł
27.
![]()
28. ![]()
29. ![]()
30. ![]()
31. ![]()
32. ![]()
36. ![]()
37. ![]()
38.
![]() 39.
39. ![]() 40.
40.
![]()
43. ![]()
46. ![]()
48. ![]()
49. ![]() zł
zł




