Zagadnienia
13. Metody stochastyczne w finansach
Liczba godzin 6.
Zakres materiału:
Funkcja użyteczności. Kryterium oczekiwanej użyteczności. Dominacja stochastyczna. Podstawowe miary ryzyka.
13.1. Strategie inwestycyjne
W tym wykładzie analizie poddane zostaną inwestycje jednookresowe.
W momencie ![]() inwestor inwestuje kwotę
inwestor inwestuje kwotę ![]() , a w ustalonym momencie
, a w ustalonym momencie ![]() otrzymuje
otrzymuje ![]() jednostek monetarnych.
Kwota
jednostek monetarnych.
Kwota ![]() jest znana (deterministyczna), a
jest znana (deterministyczna), a ![]() modelujemy jako zmienną losową.
modelujemy jako zmienną losową.
Pytanie.
Jaką metodę (strategię) ma zastosować inwestor, aby
wybrać najlepszą z wielu możliwych inwestycji?
Odpowiedź matematyka jest następująca:
Inwestor powinien wprowadzić na zbiorze wszystkich możliwych (dopuszczalnych) inwestycji
relację określającą, które z nich są ,,lepsze”, a które ,,gorsze”.
W poniższym podrozdziale omówimy własności takich relacji, a w kolejnych zajmiemy się ich konstrukcją.
13.1.1. Relacje quasi-porządku
Zastosowanie standardowych relacji porządkujących (patrz [35] rozdział IX) wymaga od inwestora informacji niejednokrotnie niemożliwych do uzyskania dlatego znacznie bardziej praktyczne jest wprowadzenie relacji quasi-porządkujących.
Definicja 13.1
Relację ![]() określoną na zbiorze
określoną na zbiorze ![]() nazywamy quasi-porządkiem, jeżeli jest
nazywamy quasi-porządkiem, jeżeli jest
a) zwrotna
b) przechodnia
Z każdą relacją quasi-porządku ![]() związane są trzy ,,pokrewne” relacje
związane są trzy ,,pokrewne” relacje ![]() ,
, ![]() i
i ![]() .
.
Zauważmy, że dla dwóch różnych elementów ![]() możliwe są cztery ewentualności, które się nawzajem wykluczają:
możliwe są cztery ewentualności, które się nawzajem wykluczają:
![]() jest lepszy,
jest lepszy, ![]() jest lepszy,
jest lepszy, ![]() i
i ![]() są tak samo dobre lub
są tak samo dobre lub ![]() i
i ![]() są nieporównywalne.
są nieporównywalne.
13.2. Podejście mikroekonomiczne
13.2.1. Oczekiwana użyteczność
Założenia:
1. Inwestor zna rozkłady prawdopodobieństwa ewentualnych inwestycji.
2. Inwestor postępuje w sposób racjonalny.
Inwestorowi przyporządkowuje się funkcję użyteczności (satysfakcji) ([30, 12])
Inwestor postępuje w sposób racjonalny, jeśli wybiera inwestycję o największej oczekiwanej użyteczności wypłaty ![]()
Do wyznaczania oczekiwanej użyteczności wykorzystuje się uogólnioną wartość oczekiwaną
([26] §1.1.3), która może przyjmować wartości zarówno skończone, jak i nieskończone (![]() ).
Uogólniona wartość oczekiwana nieujemnej zmiennej losowej jest zawsze określona,
może być skończona lub równa
).
Uogólniona wartość oczekiwana nieujemnej zmiennej losowej jest zawsze określona,
może być skończona lub równa ![]() . W przypadku dowolnych zmiennych losowych korzysta się z rozkładu
na część dodatnią i ujemną, czyli
. W przypadku dowolnych zmiennych losowych korzysta się z rozkładu
na część dodatnią i ujemną, czyli
Przypomnijmy, że dla dowolnej liczby rzeczywistej ![]()
Zauważmy, że tylko w przypadku, gdy ![]() , oczekiwana użyteczność
będzie nieokreślona (
, oczekiwana użyteczność
będzie nieokreślona (![]() ).
).
Na funkcję użyteczności ![]() nakłada się następujące warunki:
nakłada się następujące warunki:
1. ![]() jest niemalejąca: ,,inwestor preferuje większy zysk”.
jest niemalejąca: ,,inwestor preferuje większy zysk”.
2. ![]() jest wklęsła: ,,awersja do ryzyka”.
jest wklęsła: ,,awersja do ryzyka”.
Uwaga. Funkcja ![]() jest wklęsła, a
jest wklęsła, a ![]() wypukła, gdy zbiór
wypukła, gdy zbiór
jest wypukły. Jest to równoważne następującemu warunkowi:
dla dowolnych nieujemnych wag ![]() i
i ![]() (
(![]() ,
, ![]() )
)
(Więcej informacji czytelnik znajdzie w książce [38], która jest
znakomitym kompendium wiedzy o funkcjach wypukłych.)
Wklęsłość uzasadnia się tym, że tłumaczy ona pewne stylizowane fakty. Otóż każda funkcja wklęsła i niemalejąca spełnia następujące oszacowania:
Możemy je zinterpretować w następujący sposób:
,,Ta sama kwota zysku bardziej cieszy, gdy mamy mniej.”
,,Taka sama strata bardziej boli, gdy mamy mniej.”
,,Strata bardziej boli, niż zysk cieszy.”
Zauważmy, że sformułowane powyżej kryterium
oznacza, że z każdą funkcją użyteczności ![]() związaliśmy relację quasi-porządku
na zbiorze
związaliśmy relację quasi-porządku
na zbiorze ![]() zmiennych losowych, które modelują możliwe wypłaty,
zmiennych losowych, które modelują możliwe wypłaty,
Wypłata, dla której oczekiwana użyteczność jest nieokreślona, tzn.
jest nieporównywalna z innymi wypłatami. Natomiast każde dwie wypłaty o określonej oczekiwanej użyteczności (skończonej lub nieskończonej) są porównywalne.
Wniosek 13.1
Jeżeli dla ustalonej funkcji użyteczności ![]() i dla każdej zmiennej losowej z
i dla każdej zmiennej losowej z ![]() jest określona oczekiwana użyteczność, to relacja
jest określona oczekiwana użyteczność, to relacja ![]() jest spójna
jest spójna
Przez ![]() będziemy oznaczać dziedzinę efektywną
funkcji użyteczności
będziemy oznaczać dziedzinę efektywną
funkcji użyteczności ![]() , tzn. zbiór tych argumentów,
dla których funkcja
, tzn. zbiór tych argumentów,
dla których funkcja ![]() przyjmuje skończone wartości
przyjmuje skończone wartości
Niech ![]() oznacza kres dolny
oznacza kres dolny ![]() ,
,
Ponieważ funkcja ![]() jest niemalejąca, to jej dziedzina efektywna może być:
jest niemalejąca, to jej dziedzina efektywna może być:
i. zbiorem pustym (![]() );
);
ii. całą prostą rzeczywistą (![]() ,
, ![]() );
);
iii. półprostą otwartą (![]() );
);
iv. półprostą domkniętą (![]() ).
).
Przypadek i.
(![]() stała równa
stała równa ![]() ) jest nieciekawy z punktu widzenia zastosowań
i w dalszym ciągu będziemy go pomijać.
) jest nieciekawy z punktu widzenia zastosowań
i w dalszym ciągu będziemy go pomijać.
Przypadek ii.![]() jest ciągła.
jest ciągła.
Przypadek iii.
Ciągłe
jest obcięcie ![]() do dziedziny efektywnej.
do dziedziny efektywnej.
Przypadek iv.![]() obcięta do dziedziny efektywnej może być nieciągła w punkcie
obcięta do dziedziny efektywnej może być nieciągła w punkcie ![]() . Ma to miejsce gdy
. Ma to miejsce gdy
Będziemy wówczas przedstawiać funkcję ![]() jako sumę dwóch funcji niemalejących i wklęsłych,
ciągłej na
jako sumę dwóch funcji niemalejących i wklęsłych,
ciągłej na ![]() i stałej na
i stałej na ![]()
gdzie
![]() prawostronna granica
prawostronna granica ![]() w
w ![]() ,
,
![\widetilde{\varphi}(x)=\left\{\begin{array}[]{ccc}\varphi(x)&\mbox{ dla }&x>d_{\varphi}\\
\varphi(d_{\varphi}^{+})&\mbox{ dla }&x=d_{\varphi}\\
-\infty&\mbox{ dla }&x<d_{\varphi},\\
\end{array}\right.](wyklady/rka/mi/mi1538.png) |
![\kappa(x)=\left\{\begin{array}[]{ccc}0&\mbox{ dla }&x>0\\
-1&\mbox{ dla }&x=0\\
-\infty&\mbox{ dla }&x<0.\\
\end{array}\right.](wyklady/rka/mi/mi1509.png) |
Funkcje wklęsłe, ciągłe na swojej dziedzinie efektywnej, można scharakteryzować za pomocą funkcji liniowych.
Lemat 13.1
Jeśli funkcja wklęsła ![]() jest ciągła na
jest ciągła na ![]() , to istnieją ciągi liczb rzeczywistych
, to istnieją ciągi liczb rzeczywistych
![]() i
i ![]() , takie, że
, takie, że
Dowód – [23] lemat 5.2.1.
Zauważmy, że gdy zmienna losowa ![]() przyjmuje z niezerowym prawdopodobieństwem wartości z dopełnienia
przyjmuje z niezerowym prawdopodobieństwem wartości z dopełnienia ![]() ,
to oczekiwana użyteczność wynosi
,
to oczekiwana użyteczność wynosi ![]() lub jest nieokreślona
lub jest nieokreślona
Oznacza to, że inwestor z góry odrzuca możliwość wyboru inwestycji (strategii) o takiej wypłacie.
13.2.2. Własności oczekiwanej użyteczności
Omówimy teraz podstawowe własności oczekiwanej użyteczności. Szczególną uwagę zwrócimy na kryteria
pozwalające stwierdzić, czy dla danej zmiennej losowej ![]() jest ona określona.
Dla ustalenia uwagi przyjmujemy, że zmienne losowe
jest ona określona.
Dla ustalenia uwagi przyjmujemy, że zmienne losowe ![]() ,
, ![]() i
i ![]() z dalszej części rozdziału są
zdefiniowane na tej samej przestrzeni probabilistycznej
z dalszej części rozdziału są
zdefiniowane na tej samej przestrzeni probabilistycznej ![]() .
Na początek pokażemy, że oczekiwana użyteczność jest monotoniczna.
.
Na początek pokażemy, że oczekiwana użyteczność jest monotoniczna.
Twierdzenie 13.1
Jeśli prawie na pewno ![]() (tzn.
(tzn. ![]() ),
a oczekiwana użyteczność
),
a oczekiwana użyteczność ![]() jest określona i większa od
jest określona i większa od ![]() ,
to
oczekiwana użyteczność
,
to
oczekiwana użyteczność ![]() jest określona i nie mniejsza niż oczekiwana użyteczność
jest określona i nie mniejsza niż oczekiwana użyteczność ![]()
Jeśli ponadto
![]() obcięta do dziedziny efektywnej jest ściśle rosnąca,
a
obcięta do dziedziny efektywnej jest ściśle rosnąca,
a ![]() i
i ![]() są istotnie różne (
są istotnie różne (![]() )
oraz oczekiwana użyteczność
)
oraz oczekiwana użyteczność ![]() jest skończona, to
jest skończona, to
Dowód.
Ponieważ ![]() ma oczekiwaną użyteczność różną od
ma oczekiwaną użyteczność różną od ![]() , to prawie na pewno
nie przyjmuje wartości z dopełnienia dziedziny efektywnej
, to prawie na pewno
nie przyjmuje wartości z dopełnienia dziedziny efektywnej ![]() . A skoro
. A skoro
![]() jest niemalejąca, to otrzymujemy następujące nierówności
jest niemalejąca, to otrzymujemy następujące nierówności
Zatem zmienna losowa ![]() jest prawie na pewno nieujemna i
ma nieujemną wartość oczekiwaną (skończoną lub nieskończoną)
jest prawie na pewno nieujemna i
ma nieujemną wartość oczekiwaną (skończoną lub nieskończoną)
Ponieważ ![]() , to oczekiwana użyteczność
, to oczekiwana użyteczność ![]() jest określona i jest od niej nie większa
jest określona i jest od niej nie większa
Gdy ![]() i
i ![]() są istotnie różne, a
są istotnie różne, a
![]() obcięta do dziedziny efektywnej jest ściśle rosnąca,
to
obcięta do dziedziny efektywnej jest ściśle rosnąca,
to
Zatem
Ponieważ
oczekiwana użyteczność ![]() jest skończona,
to otrzymujemy ,,ostrą” nierówność
jest skończona,
to otrzymujemy ,,ostrą” nierówność
Przeformułujemy teraz powyższe twierdzenie w terminach quasi-porządku.
Wniosek 13.2
Jeżeli oczekiwane użyteczności ![]() i
i ![]() są określone i prawie na pewno
są określone i prawie na pewno![]() , to
, to
Ponadto, jeśli ![]() jest ściśle rosnąca, a
jest ściśle rosnąca, a ![]() są istotnie różne
i mają skończone oczekiwane użyteczności,
to
są istotnie różne
i mają skończone oczekiwane użyteczności,
to
Zauważmy, że z powyższego twierdzenia wynika prosty warunek dostateczny istnienia oczekiwanej użyteczności.
Wniosek 13.3
Jeżeli prawie na pewno ![]() nie przyjmuje wartości mniejszych niż pewna stała
nie przyjmuje wartości mniejszych niż pewna stała ![]() należąca do efektywnej
dziedziny
należąca do efektywnej
dziedziny ![]() , to
oczekiwana użyteczność
, to
oczekiwana użyteczność ![]() jest określona i różna od
jest określona i różna od ![]() .
.
Dowód.
Skoro ![]() należy do dziedziny efektywnej
należy do dziedziny efektywnej ![]() , to
użyteczność wypłaty
, to
użyteczność wypłaty ![]() jest większa od
jest większa od
![]() . Zatem z powyższego twierdzenia otrzymujemy, że oczekiwana użyteczność wypłaty
. Zatem z powyższego twierdzenia otrzymujemy, że oczekiwana użyteczność wypłaty ![]() jest określona i nie mniejsza od
jest określona i nie mniejsza od ![]() . Czyli
. Czyli
Twierdzenie 13.2
Jeżeli zmienna losowa ![]() ma skończoną wartość oczekiwaną (tzn.
ma skończoną wartość oczekiwaną (tzn. ![]() )
to spełnione są następujące warunki:
)
to spełnione są następujące warunki:
i. oczekiwana użyteczność ![]() jest określona;
jest określona;
ii. ![]() ;
;
iii. dla dowolnego ![]() -ciała
-ciała ![]() ,
, ![]() ,
jest określona oczekiwana użyteczność warunkowej wartości oczekiwanej
,
jest określona oczekiwana użyteczność warunkowej wartości oczekiwanej ![]() i
i
![]() .
.
Ponadto, jeśli ![]() jest ściśle wklęsła, a
jest ściśle wklęsła, a ![]() nie jest stała i
nie jest stała i
![]() , to
, to![]() .
.
Uwagi.
1. Funkcja wklęsła jest ściśle wklęsła, gdy na żadnym przedziale nie jest liniowa,
tzn. gdy prosta styczna do wykresu ma z nim tylko jeden punkt wspólny.
2. Punkt iii. oznacza, że jeśli uśrednimy wypłatę, to
jej oczekiwana
użyteczność nie zmaleje.
Dowód.
Ad ii. oraz i.
Jeżeli ![]() ma skończoną oczekiwaną użyteczność, to ii. wynika z nierówności Jensena dla funkcji
ma skończoną oczekiwaną użyteczność, to ii. wynika z nierówności Jensena dla funkcji ![]() .
Ponieważ zakładamy tylko istnienie skończonej wartości oczekiwanej
.
Ponieważ zakładamy tylko istnienie skończonej wartości oczekiwanej ![]() , to musimy
pokazać istnienie oczekiwanej użyteczności.
, to musimy
pokazać istnienie oczekiwanej użyteczności.
Niech ![]() ,
,
bedzie równaniem prostej stycznej do wykresu ![]() w punkcie
w punkcie ![]() ,
, ![]() .
.
![]() jest wklęsła, zatem jej wykres leży poniżej lub na prostej stycznej
jest wklęsła, zatem jej wykres leży poniżej lub na prostej stycznej
Zatem zmienna losowa ![]() jest niedodatnia i ma wartość oczekiwaną (w
jest niedodatnia i ma wartość oczekiwaną (w ![]() ),
),
Ale jak łatwo zauważyć, ![]() ma skończoną wartość oczekiwaną
ma skończoną wartość oczekiwaną
Z tego wynika, że istnieje oczekiwana użyteczność ![]() i spełnia nierówność
i spełnia nierówność
Gdy ![]() , to podstawiamy
, to podstawiamy ![]() i otrzymujemy warunek ii.
W przeciwnym przypadku, gdy
i otrzymujemy warunek ii.
W przeciwnym przypadku, gdy ![]() ,
to albo z dodatnim prawdopodobieństwem
,
to albo z dodatnim prawdopodobieństwem ![]() przyjmuje wartości z dopełnienia dziedziny efektywnej
przyjmuje wartości z dopełnienia dziedziny efektywnej ![]() ,
wówczas oczekiwana użyteczność
,
wówczas oczekiwana użyteczność ![]() jest równa
jest równa ![]() i warunek ii. też jest spełniony
i warunek ii. też jest spełniony
albo ![]() jest prawie na pewno stała,
jest prawie na pewno stała, ![]() ,
a zatem
,
a zatem ![]() .
.
Ad iii.
Dowód punktu iii. jest trochę bardziej skomplikowany.
![]() , a więc warunkowa wartość oczekiwana
, a więc warunkowa wartość oczekiwana ![]() jest określona i też należy do
jest określona i też należy do ![]() ,
,
Zatem jej oczekiwana użyteczność jest określona i nie większa niż ![]() (punkt (i)).
Gdy
oczekiwana użyteczność
(punkt (i)).
Gdy
oczekiwana użyteczność ![]() jest równa
jest równa ![]() , to warunek (iii) jest automatycznie spełniony.
W przeciwnym przypadku, gdy zarówno
, to warunek (iii) jest automatycznie spełniony.
W przeciwnym przypadku, gdy zarówno ![]() i
i ![]() są skończone, korzystamy z nierówności Jensena
dla warunkowej wartości oczekiwanej dla
są skończone, korzystamy z nierówności Jensena
dla warunkowej wartości oczekiwanej dla ![]() ([23, lemat 5.2.2])
([23, lemat 5.2.2])
Następnie korzystamy z twierdzenia o iterowaniu wartości oczekiwanej i otrzymujemy następującą nierówność
Co kończy dowód iii.
Gdy ![]() jest ściśle wklęsła, to
jest ściśle wklęsła, to
Ponadto rozkład ![]() nie jest skupiony w jednym punkcie
nie jest skupiony w jednym punkcie
zatem
A z tego wynika, że dla ![]() otrzymujemy
otrzymujemy
Przeformułujemy powyższe twierdzenie w terminach quasi-porządku.
Wniosek 13.4
Jeżeli ![]() i
i ![]() są skończone, to
są skończone, to
Ponadto, jeśli ![]() jest ściśle wklęsła, a
jest ściśle wklęsła, a ![]() nie jest stała, to
nie jest stała, to
Z powyższego twierdzenia wynika również następująca charakteryzacja niechęci (awersji) do ryzyka.
Wniosek 13.5
Inwestor, który planuje inwestycje w oparciu o ściśle wklęsłą funkcję użyteczności,
mając do wyboru inwestycję pewną o znanej z góry wypłacie ![]() i inwestycję
wymagającą takich samych nakładów, o tym samym czasie życia i o
losowej (nieznanej) wypłacie
i inwestycję
wymagającą takich samych nakładów, o tym samym czasie życia i o
losowej (nieznanej) wypłacie ![]() o
wartości oczekiwanej
o
wartości oczekiwanej ![]() , wybierze tę pierwszą.
, wybierze tę pierwszą.
Natomiast z punktu iii. twierdzenia 13.2 wynika warunkowa monotoniczność oczekiwanej użyteczności.
Wniosek 13.6
Jeżeli para ![]() jest nadmartyngałem, tzn.
jest nadmartyngałem, tzn.
oraz ![]() ma skończoną zarówno wartość oczekiwaną jak i oczekiwaną użyteczność,
to oczekiwana użyteczność
ma skończoną zarówno wartość oczekiwaną jak i oczekiwaną użyteczność,
to oczekiwana użyteczność ![]() jest określona i nie mniejsza niż
oczekiwana użyteczność
jest określona i nie mniejsza niż
oczekiwana użyteczność ![]()
Dowód.
Z twierdzenia 13.2 wynika, że oczekiwana użyteczność ![]() istnieje
i spełnia nierówność
istnieje
i spełnia nierówność
Natomiast z twierdzenia 13.1 otrzymujemy istnienie ![]() i oszacowanie
i oszacowanie
Co kończy dowód.
Z twierdzenia 13.2 wynika tylko górne ograniczenie na oczekiwaną użyteczność. Dolne ograniczenie
może nie istnieć. Okazuje się, że skończona wartość oczekiwana wypłaty ![]() wcale nie musi implikować
skończonej oczekiwanej użyteczności nawet, jeśli
wcale nie musi implikować
skończonej oczekiwanej użyteczności nawet, jeśli ![]() nie przyjmuje wartości spoza dziedziny efektywnej
nie przyjmuje wartości spoza dziedziny efektywnej
![]() (- patrz ćwiczenie 13.5).
(- patrz ćwiczenie 13.5).
Na zakończenie pokażemy, że oczekiwana użyteczność jest wklęsła.
Twierdzenie 13.3
Jeżeli zmienne losowe ![]() i
i ![]() mają skończoną oczekiwaną użyteczność to
dla dowolnych wag
mają skończoną oczekiwaną użyteczność to
dla dowolnych wag ![]() i
i ![]() (
(![]() ,
, ![]() )
)
i. zmienna losowa ![]() ma określoną oczekiwaną użyteczność,
ma określoną oczekiwaną użyteczność,
ii. ![]() .
.
Ponadto, jeśli ![]() jest ściśle wklęsła,
jest ściśle wklęsła, ![]() i
i ![]() są istotnie różne,
są istotnie różne,
![]() ,
a wagi
,
a wagi ![]() dodatnie,
to
dodatnie,
to
![]() .
.
Dowód.![]() jest funkcją wklęsłą czyli
dla dowolnych wag
jest funkcją wklęsłą czyli
dla dowolnych wag ![]() i
i ![]()
Zatem zmienna losowa
![]() jest nieujemna i ma nieujemną wartość oczekiwaną.
Zatem
jest nieujemna i ma nieujemną wartość oczekiwaną.
Zatem
Gdy ![]() jest funkcją ściśle wklęsłą, to dla
jest funkcją ściśle wklęsłą, to dla ![]() ,
, ![]() i
i
![]()
Zatem nieujemna zmienna losowa
![]() jest dodatnia na zbiorze,
który ma dodatnią miarę.
Zatem jej wartość oczekiwana jest dodatnia i nierówność z punktu ii. jest ostra.
jest dodatnia na zbiorze,
który ma dodatnią miarę.
Zatem jej wartość oczekiwana jest dodatnia i nierówność z punktu ii. jest ostra.
Wniosek 13.7
Jeżeli istotnie różne zmienne losowe ![]() i
i ![]() mają równe skończone oczekiwane użyteczności,
a
mają równe skończone oczekiwane użyteczności,
a ![]() jest ściśle wklęsła,
to
dla dowolnych dodatnich wag
jest ściśle wklęsła,
to
dla dowolnych dodatnich wag ![]() i
i ![]() (
(![]() ,
, ![]() )
)
Dowód.
Niech ![]() oczekiwana użyteczność
oczekiwana użyteczność ![]() i
i ![]() . Z powyższego twierdzenia
wynika, że
. Z powyższego twierdzenia
wynika, że
Zatem kombinacja wypukła ![]() i
i ![]() jest od nich obu ,,lepsza”.
jest od nich obu ,,lepsza”.
Z powyższego wniosku wynika następująca zasada dywersyfikacji portfela.
Wniosek 13.8
Inwestor, który planuje inwestycje w oparciu o ściśle wklęsłą funkcję użyteczności,
mając do wyboru trzy inwestycje wymagające takich samych nakładów, o tym samym czasie życia
i o istotnie różnych wypłatach ![]() ,
, ![]() i
i ![]() ,
takich, że oczekiwane użyteczności
,
takich, że oczekiwane użyteczności ![]() i
i ![]() są skończone i równe, a
są skończone i równe, a ![]() jest
kombinacją wypukłą
jest
kombinacją wypukłą ![]() i
i ![]() ,
wybierze tę trzecią.
,
wybierze tę trzecią.
13.3. Ćwiczenia
Ćwiczenie 13.1
Niech ![]() i
i ![]() będą zmiennymi losowymi zero-jedynkowymi
będą zmiennymi losowymi zero-jedynkowymi
a ![]() dowolną funkcją użyteczności taką, że
dowolną funkcją użyteczności taką, że ![]() .
Pokazać, że
.
Pokazać, że
Rozwiązanie.
Dla zmiennej losowej zero-jedynkowej oczekiwana użyteczność wynosi
![]() jest niemalejąca. Zatem gdy
jest niemalejąca. Zatem gdy ![]() , to oczekiwana użyteczność
, to oczekiwana użyteczność
![]() jest większa lub równa oczekiwanej użyteczności
jest większa lub równa oczekiwanej użyteczności ![]() . A stąd
. A stąd
Ćwiczenie 13.2
Niech ![]() i
i ![]() będą zmiennymi losowymi zero-jedynkowymi
będą zmiennymi losowymi zero-jedynkowymi
a ![]() dowolną funkcją użyteczności taką, że
dowolną funkcją użyteczności taką, że ![]() .
Pokazać, że gdy zmienne losowe
.
Pokazać, że gdy zmienne losowe ![]() mają taką samą oczekiwaną użyteczność,
to mają takie samo prawdopodobieństwo osiągnięcia sukcesu.
mają taką samą oczekiwaną użyteczność,
to mają takie samo prawdopodobieństwo osiągnięcia sukcesu.
Rozwiązanie.
Zatem z równości oczekiwanych użyteczności otrzymujemy
Ćwiczenie 13.3
Wyznaczyć oczekiwaną użyteczność ![]() , gdy
, gdy ![]() ma rozkład normalny
ma rozkład normalny ![]() a
a ![]() , gdzie
, gdzie ![]() ustalony parametr rzeczywisty.
ustalony parametr rzeczywisty.
Rozwiązanie.
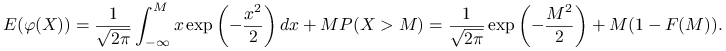 |
Odpowiedź.
Oczekiwana użyteczność ![]() wynosi
wynosi ![]() ,
gdzie
,
gdzie ![]() jest dystrybuantą standardowego rozkładu normalnego.
jest dystrybuantą standardowego rozkładu normalnego.
Ćwiczenie 13.4
Inwestor podejmuje decyzje w oparciu o logarytmiczną funkcję użyteczności
Może zainwestować 1000 zł w dwie inwestycje, o tym samym czasie życia. Wypłata z pierwszej ma rozkład
| 960 | 980 | 1000 | 1030 | 1050 | |
|---|---|---|---|---|---|
| prawdopodobieństwo [%] | 20 | 10 | 15 | 25 | 30 |
a z drugiej
| 960 | 970 | 990 | 1000 | 1010 | 1040 | 1050 | 1060 | |
|---|---|---|---|---|---|---|---|---|
| prawd. [%] | 15 | 5 | 5 | 15 | 5 | 25 | 20 | 10 |
Którą z inwestycji wybierze?
Rozwiązanie. Wyznaczamy oczekiwane użyteczności:
Jak widać, oczekiwana użyteczność drugiej wypłaty jest trochę większa.
Odpowiedź.
Inwestor wybierze drugą inwestycję.
Ćwiczenie 13.5
Wyznaczyć oczekiwaną użyteczność dla wypłaty ![]() , która ma rozkład jednostajny
na przedziale
, która ma rozkład jednostajny
na przedziale ![]()
![P(K\leq x)=\left\{\begin{array}[]{ccc}0&\mbox{ dla }&x\leq 0\\
\frac{1}{2}x&\mbox{ dla }&0<x<2\\
1&\mbox{ dla }&2\leq x\\
\end{array}\right.](wyklady/rka/mi/mi1512.png) |
i dla funkcji użyteczności
Porównać ją z użytecznością wartości oczekiwanej ![]() .
.
Rozwiązanie. Gęstość prawdopodobieństwa rozkładu jednostajnego na przedziale o długości 2 jest równa 0,5 wewnątrz tego przedziału i 0 poza nim. Zatem
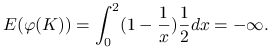 |
Z drugiej strony wartość oczekiwana ![]() wynosi 1, a więc
wynosi 1, a więc
Odpowiedź.
Oczekiwana użyteczność dla wypłaty ![]() wynosi
wynosi ![]() , podczas gdy użyteczność wartości oczekiwanej
, podczas gdy użyteczność wartości oczekiwanej ![]() wynosi 0.
wynosi 0.





