Zagadnienia
14. Metody stochastyczne w finansach - cd
14.1. Dominacja stochastyczna
Oczekiwana użyteczność zależy od wyboru funkcji użyteczności.
Zachodzi pytanie, czy można ocenić, która z dwóch inwestycji jest lepsza dla wszystkich
inwestorów niezależnie od ich indywidualnych preferencji.
Postaramy się odpowiedzieć na to pytanie, korzystając z pojęcia dominacji stochastycznej.
Niech ![]() i
i ![]() oznaczają zmienne losowe.
oznaczają zmienne losowe.
Definicja 14.1
Mówimy, że ![]() dominuje nad
dominuje nad ![]() gdy
gdy
czyli ![]() .
.
Definicja 14.2
Mówimy, że ![]() dominuje nad
dominuje nad ![]() w sensie dominacji stochastycznej rzędu pierwszego,
gdy
w sensie dominacji stochastycznej rzędu pierwszego,
gdy
gdzie ![]() oznacza dystrybuantę zmiennej losowej
oznacza dystrybuantę zmiennej losowej ![]() .
.
Piszemy wówczas:
Relacja FSD nie zależy od wyboru definicji dystrybuanty. Jeżeli
![]() dominuje nad
dominuje nad ![]() w sensie dominacji stochastycznej rzędu pierwszego dla dystybuant prawostronnie ciągłych
(
w sensie dominacji stochastycznej rzędu pierwszego dla dystybuant prawostronnie ciągłych
(![]() ), to
dominuje również
w sensie dominacji stochastycznej rzędu pierwszego dla dystybuant lewostronnie ciągłych
(
), to
dominuje również
w sensie dominacji stochastycznej rzędu pierwszego dla dystybuant lewostronnie ciągłych
(![]() ) i na odwrót. Ale dla ustalenia uwagi, w dalszym ciągu
będziemy używać dystrybuant prawostronnie ciągłych (zgodnie z [21, 26]).
) i na odwrót. Ale dla ustalenia uwagi, w dalszym ciągu
będziemy używać dystrybuant prawostronnie ciągłych (zgodnie z [21, 26]).
Dystrybuanta ![]() jest funkcją nieujemną i ograniczoną, zatem zawsze istnieje granica skończona lub nieskończona
całek
jest funkcją nieujemną i ograniczoną, zatem zawsze istnieje granica skończona lub nieskończona
całek ![]() gdy
gdy ![]() zbiega do
zbiega do ![]() , czyli uogólniona całka niewłaściwa
, czyli uogólniona całka niewłaściwa
![]() jest zawsze określona.
jest zawsze określona.
Definicja 14.3
Mówimy, że ![]() dominuje nad
dominuje nad ![]() w sensie dominacji stochastycznej rzędu drugiego,
gdy
w sensie dominacji stochastycznej rzędu drugiego,
gdy
gdzie ![]() dystrybuanta
dystrybuanta ![]() , a całki są całkami uogólnionymi.
, a całki są całkami uogólnionymi.
Piszemy wówczas:
Zauważmy, że w przypadku dominacji stochastycznej rzędu pierwszego i drugiego
zmienne losowe ![]() i
i ![]() nie muszą być
określone na tej samej przestrzeni probabilistycznej.
Ponadto, jeśli nawzajem nad sobą dominują, to mają ten sam rozkład (
nie muszą być
określone na tej samej przestrzeni probabilistycznej.
Ponadto, jeśli nawzajem nad sobą dominują, to mają ten sam rozkład (![]() ).
Zatem relacje dominacji stochastycznej, rzędu pierwszego i drugiego,
są relacjami quasi-porządku na zbiorach zmiennych losowych, indukującymi relacje
częściowego porządku na zbiorach ich rozkładów.
).
Zatem relacje dominacji stochastycznej, rzędu pierwszego i drugiego,
są relacjami quasi-porządku na zbiorach zmiennych losowych, indukującymi relacje
częściowego porządku na zbiorach ich rozkładów.
Uwaga.
Mamy następujące zależności:
Pokażemy teraz, jakie związki zachodzą między kryterium maksymalizacji oczekiwanej użyteczności a dominacją stochastyczną pierwszego i drugiego rzędu.
Twierdzenie 14.1
Niech ![]() i
i ![]() zmienne losowe. Wówczas
następujące warunki są równoważne:
zmienne losowe. Wówczas
następujące warunki są równoważne:
1. ![]() ;
;
2. Dla każdej niemalejącej funkcji ![]() mamy:
mamy:![]() lub obie wartości oczekiwane są nieokreślone
lub
lub obie wartości oczekiwane są nieokreślone
lub ![]() lub
lub ![]() ;
;
3. Istnieją zmienne losowe ![]() i
i ![]() o tym samym rozkładzie co odpowiednio
o tym samym rozkładzie co odpowiednio ![]() i
i ![]() , takie, że
, takie, że
Dowód.
1![]() 3.
3.
Skorzystamy ze standardowej konstrukcji (patrz [21] §5.3 zad. 2).
Zmienne losowe ![]() i
i ![]() zdefiniujemy na nowej przestrzeni probabilistycznej.
Jako zbiór zdarzeń elementarnych weźmiemy otwarty odcinek jednostkowy (
zdefiniujemy na nowej przestrzeni probabilistycznej.
Jako zbiór zdarzeń elementarnych weźmiemy otwarty odcinek jednostkowy (![]() ), a jako prawdopodobieństwo
miarę Lebesgue'a
), a jako prawdopodobieństwo
miarę Lebesgue'a ![]() na tym odcinku. Niech
na tym odcinku. Niech
Jak łatwo sprawdzić, ![]() i
i ![]() mają ten sam rozkład prawdopodobieństwa. Rzeczywiście
dla dowolnego
mają ten sam rozkład prawdopodobieństwa. Rzeczywiście
dla dowolnego ![]()
Pozostaje pokazać, że ![]() dominuje nad
dominuje nad ![]() .
Z pierwszej dominacji stochastycznej
.
Z pierwszej dominacji stochastycznej ![]() wynika, że
wynika, że
Zatem
czyli dla dowolnego ![]()
![]() .
.
3![]() 2.
2.
Wartość oczekiwana zależy tylko od rozkładu, ![]() i
i ![]() mają ten sam rozkład,
a więc
mają ten sam rozkład,
a więc ![]() lub obie są nieokreślone.
Ponadto
lub obie są nieokreślone.
Ponadto ![]() jest niemalejąca, zatem gdy wartości oczekiwane istnieją, to
jest niemalejąca, zatem gdy wartości oczekiwane istnieją, to
2![]() 1.
1.
Zauważmy, że funkcje
są niemalejące. Zatem dla dowolnego ![]()
co daje ![]() .
.
Wniosek 14.1
Niech ![]() ,
, ![]() , będzie funkcją niemalejącą taką, że
zmienne losowe
, będzie funkcją niemalejącą taką, że
zmienne losowe ![]() i
i ![]() prawie na pewno przyjmują wartości z
prawie na pewno przyjmują wartości z ![]()
Wówczas
W szczególności dla ![]() i
i ![]()
Dowód.
Skorzystamy z pkt. 3 powyższego twierdzenia.
Jeśli
![]() i
i ![]() mają ten sam rozkład co odpowiednio
mają ten sam rozkład co odpowiednio ![]() i
i ![]() i
i
to
![]() i
i ![]() mają ten sam rozkład co odpowiednio
mają ten sam rozkład co odpowiednio ![]() i
i ![]() i
i
Zatem
Przejdziemy teraz do drugiej dominacji stochastycznej. Na początek pokażemy związek między całką z dystrybuanty, a wartością oczekiwaną.
Lemat 14.1
Dla dowolnej zmiennej losowej ![]() o dystrybuancie
o dystrybuancie ![]()
Dowód.
Jak wiadomo ([21] Stwierdzenie 11 §5.6) wartość oczekiwana nieujemnej zmiennej losowej ![]() jest równa całce z prawdopodobieństwa przekroczenia poziomu
jest równa całce z prawdopodobieństwa przekroczenia poziomu ![]() po
po ![]() ,
,
Część ujemna ![]() jest z definicji nieujemna, zatem
jest z definicji nieujemna, zatem
Ponieważ ![]() , to
, to ![]() wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy ![]() i
i
Po zamianie zmiennych, ![]() , otrzymujemy
, otrzymujemy
gdyż poza przeliczalną liczbą punktów ![]() .
.
Z powyższego wynika następująca charakteryzacja drugiej dominacji stochastycznej:
Wniosek 14.2
Pokażemy teraz, że gdy ![]() ma skończoną wartość oczekiwaną,
to funkcja
ma skończoną wartość oczekiwaną,
to funkcja
ma prawostronną asymptotę ukośną ![]() .
.
Lemat 14.2
Dla dowolnej zmiennej losowej ![]() o dystrybuancie
o dystrybuancie ![]() i skończonej wartości oczekiwanej (
i skończonej wartości oczekiwanej (![]() )
)
Dowód.
Załóżmy, że ![]() . Wówczas
. Wówczas
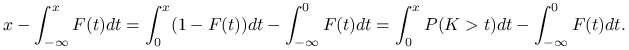 |
Dla ![]()
![]() wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy ![]() , zatem
korzystając ponownie ze stwierdzenia 11 §5.6 [21] otrzymujemy dla
, zatem
korzystając ponownie ze stwierdzenia 11 §5.6 [21] otrzymujemy dla ![]() zbiegającego do
zbiegającego do ![]()
Ponieważ, jak pokazaliśmy w poprzednim lemacie
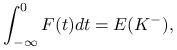 |
to
Wniosek 14.3
Twierdzenie 14.2
Niech ![]() i
i ![]() zmienne losowe o skończonych wartościach oczekiwanych (
zmienne losowe o skończonych wartościach oczekiwanych (![]() ). Wówczas
następujące warunki są równoważne:
). Wówczas
następujące warunki są równoważne:
1. ![]() ;
;
2. Dla każdej niemalejącej i wklęsłej funkcji ![]()
![]() ;
;
3. Istnieją zmienne losowe ![]() i
i ![]() o tym samym rozkładzie co odpowiednio
o tym samym rozkładzie co odpowiednio ![]() i
i ![]() , takie, że
, takie, że
tzn. para ![]() jest nadmartyngałem.
jest nadmartyngałem.
Wniosek 14.4
Niech
![]() i
i ![]() zmienne losowe o skończonych wartościach oczekiwanych (
zmienne losowe o skończonych wartościach oczekiwanych (![]() ), a
), a
![]() ,
, ![]() funkcja niemalejąca i wklęsła taka, że
zmienne losowe
funkcja niemalejąca i wklęsła taka, że
zmienne losowe ![]() i
i ![]() prawie na pewno przyjmują wartości z
prawie na pewno przyjmują wartości z ![]()
Wówczas
W szczególności dla ![]() i
i ![]()
Dowód.
Zauważmy, że wzięta ze znakiem przeciwnym część ujemna z funkcji niemalejącej i wklęsłej też jest niemalejąca i wklęsła.
Zatem z dominacji stochastycznej, ![]() , wynika, że dla każdego
, wynika, że dla każdego ![]()
co jest równoważne
dominacji stochastycznej, ![]() .
.
Na zakończenie pokażemy, że dominację stochastyczną pierwszego lub drugiego rzędu
można stosować wymiennie do oceny wypłat z inwestycji lub zysku lub stóp zwrotu.
Niech ![]() i
i ![]() modelują wypłaty z dwóch inwestycji A i B, wymagających
tych samych nakładów
modelują wypłaty z dwóch inwestycji A i B, wymagających
tych samych nakładów ![]() ,
, ![]() .
.
Przez ![]() i
i ![]() oznaczamy odpowiednio zysk i stopę zwrotu
oznaczamy odpowiednio zysk i stopę zwrotu
Załóżmy, że dystrybuanty ![]() i
i ![]() są różne od siebie tzn.
są różne od siebie tzn.
Wówczas:
Wniosek 14.5
Jeżeli zachodzi choć jeden z poniższych warunków![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,
to
racjonalny inwestor wybierze inwestycję A.
Załóżmy ponadto, że wartości oczekiwane ![]() i
i ![]() są skończone.
są skończone.
Wniosek 14.6
Jeżeli zachodzi choć jeden z poniższych warunków![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,
to
racjonalny inwestor wybierze inwestycję A.
14.2. Własności dominacji stochastycznej
Rozważania w tym podrozdziale ograniczymy do zmiennych losowych całkowalnych, tzn. posiadających skończoną wartość oczekiwaną.
Definicja 14.4
Semiwariancją ujemną i dodatnią zmiennej losowej ![]() nazywamy odpowiednio
nazywamy odpowiednio
Pierwiastek z semiwariancji nazywamy semiodchyleniem standardowym
Jeśli zmienna losowa ![]() ma rozkład symetryczny, to semiwariancje są sobie równe i wynoszą połowę wariancji
ma rozkład symetryczny, to semiwariancje są sobie równe i wynoszą połowę wariancji
Gdy w definicji wariancji zastąpimy kwadrat przez moduł, to otrzymamy odchylenie przeciętne. Przypomnijmy:
Definicja 14.5
Odchyleniem przeciętnym,
semiodchyleniem przeciętnym
ujemnym i semiodchyleniem przeciętnym
dodatnim zmiennej losowej ![]() nazywamy odpowiednio
nazywamy odpowiednio
Te trzy wielkości są ściśle ze sobą związane.
Lemat 14.3
Dla dowolnej zmiennej losowej ![]()
Dowód. Zauważmy, że
Natomiast
Zatem
Przeanalizujemy teraz zależności między parametrami rozkładów wynikające z dominacji stochastycznej pierwszego lub drugiego rzędu.
Lemat 14.4
Jeśli ![]() dominuje stochastycznie nad
dominuje stochastycznie nad ![]() ,
,
![]() ,
to
,
to
1. ![]() .
.
Jeśli ponadto ![]() , to
, to
2. ![]() ;
;
3. ![]() ;
;
4. ![]() .
.
Dowód.
Ad 1.
Rozważamy funkcję ![]() . Jest to funkcja rosnąca, zatem
. Jest to funkcja rosnąca, zatem
W dalszej części dowodu przyjmiemy, że wartości oczekiwane są równe,![]() .
.
Ad 2.
Rozważamy funkcję ![]() .
Jest to funkcja niemalejąca, zatem
.
Jest to funkcja niemalejąca, zatem
Ad 3.
Rozważamy funkcję ![]() . Jest to funkcja niemalejąca, zatem
. Jest to funkcja niemalejąca, zatem
Ad 4.
Rozważamy funkcje ![]() i
i ![]() .
Obie są funkcjami niemalejącymi, a więc
.
Obie są funkcjami niemalejącymi, a więc
Zatem ![]() , czyli również
, czyli również ![]() .
.
Druga dominacja stochastyczna implikuje trochę słabsze warunki.
Lemat 14.5
Jeśli ![]() dominuje stochastycznie nad
dominuje stochastycznie nad ![]() ,
,
![]() ,
to
,
to
1. ![]() .
.
Jeśli ponadto ![]() , to
, to
2. ![]() ;
;
3. ![]() .
.
Dowód.
Nierówność dla wartości oczekiwanych była pokazana już w poprzednim podrozdziale (wniosek 14.3).
Nierówności 2 i 3 wynikają z faktu, że
funkcje ![]() i
i ![]() wykorzystane do dowodu 2 i 4 w poprzednim lemacie są
nie tylko niemalejące, ale i wklęsłe.
wykorzystane do dowodu 2 i 4 w poprzednim lemacie są
nie tylko niemalejące, ale i wklęsłe.
Gdy rozkłady są symetryczne, to semiodchylenia standardowe można zastąpić odchyleniem standardowym.
Wniosek 14.7
Jeśli rozkłady ![]() i
i ![]() są symetryczne,
są symetryczne, ![]() i
i ![]() ,
to
,
to
![]() .
.
Wniosek 14.8
Jeśli rozkłady ![]() i
i ![]() są symetryczne,
są symetryczne, ![]() i
i ![]() ,
to
,
to
![]() .
.
W przypadku rozkładów normalnych dominację stochastyczną można całkowicie opisać w terminach wartości oczekiwanej i odchylenia standardowego.
Twierdzenie 14.3
Niech zmienne losowe ![]() i
i ![]() mają rozkłady normalne o parametrach
mają rozkłady normalne o parametrach
Wówczas
Dowód.
Niech ![]() oznacza dystrybuantę rozkładu normalnego standardowego
oznacza dystrybuantę rozkładu normalnego standardowego ![]() .
Dystrybuanty zmiennych
.
Dystrybuanty zmiennych ![]() możemy zapisać w następujący sposób
możemy zapisać w następujący sposób
Dystrybuanta ![]() jest ściśle rosnąca, zatem
jest ściśle rosnąca, zatem
Druga dominacja jest bardziej skomplikowana. Zauważmy, że
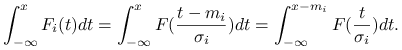 |
Najpierw pokażemy, że z nierówności
wynika druga dominacja stochastyczna.
Pokażemy, że pochodna po ![]() jest nieujemna
jest nieujemna
Zatem przy ustalonych ![]() i
i ![]() zależność od
zależność od ![]() jest monotoniczna. A więc
jest monotoniczna. A więc
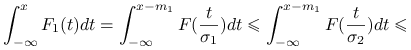 |
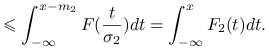 |
Dowód implikacji w drugą stronę. Jak pokazaliśmy powyżej, druga dominacja stochastyczna implikuje nierówność wartości oczekiwanych.
Rozważmy następującą granicę, gdy ![]() dąży do
dąży do ![]()
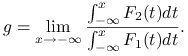 |
Stosując dwukrotnie regułę de l'Hospitala, otrzymujemy
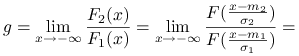 |
![=\left\{\begin{array}[]{ccc}0&\mbox{ dla }&\sigma _{1}>\sigma _{2}\\
0&\mbox{ dla }&\sigma _{1}=\sigma _{2}\wedge m_{1}<m_{2}\\
1&\mbox{ dla }&\sigma _{1}=\sigma _{2}\wedge m_{1}=m_{2}\\
+\infty&\mbox{ dla }&\sigma _{1}=\sigma _{2}\wedge m_{1}>m_{2}\\
+\infty&\mbox{ dla }&\sigma _{1}<\sigma _{2}\end{array}\right.](wyklady/rka/mi/mi1651.png) |
Z drugiej dominacji stochastycznej wynika, że ![]() jest nie mniejsze od 1. Zatem przypadek
jest nie mniejsze od 1. Zatem przypadek
![]() można wykluczyć.
można wykluczyć.
Na zakończenie zajmiemy się zmiennymi losowymi o rozkładzie lognormalnym.
Twierdzenie 14.4
Niech
![]() i
i ![]() zmienne losowe o rozkładzie lognormalnym,
zmienne losowe o rozkładzie lognormalnym,![]() , gdzie zmienne losowe
, gdzie zmienne losowe ![]() mają rozkład normalny o parametrach
mają rozkład normalny o parametrach
Wówczas
Dowód.
Równoważność dla dominacji stochastycznej pierwszego rzędu wynika z faktu, że funkcja wykładnicza jest
rosnąca i odwracalna. Zatem z wniosku 14.1 i charakteryzacji dominacji stochastycznej
dla rozkładów normalnych (twierdzenie 14.3) otrzymujemy:
W przypadku dominacji stochastycznej drugiego rzędu
dominacja ![]() nad
nad ![]() nie jest równoważna dominacji
nie jest równoważna dominacji ![]() and
and ![]() .
Prawdziwa jest tylko implikacja w jedną stronę, która wynika z faktu, że
.
Prawdziwa jest tylko implikacja w jedną stronę, która wynika z faktu, że ![]() , a
logarytm naturalny jest funkcją rosnąca i wklęsła. Z wniosku 14.4 i twierdzenia 14.3
otrzymujemy:
, a
logarytm naturalny jest funkcją rosnąca i wklęsła. Z wniosku 14.4 i twierdzenia 14.3
otrzymujemy:
Ponadto z dominacji stochastycznej wynika nierowność dla wartości oczekiwanych
Przypomnimy, że
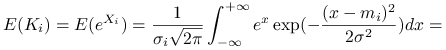 |
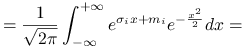 |
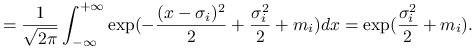 |
Zatem
Co kończy dowód implikacji w prawą stronę.
Pokażemy teraz, że warunki na parametry ![]() i
i ![]() wystarczają, aby zachodziła dominacja stochastyczna
rzędu drugiego. Skorzystamy z warunku 3 twierdzenia 14.2. Niech
wystarczają, aby zachodziła dominacja stochastyczna
rzędu drugiego. Skorzystamy z warunku 3 twierdzenia 14.2. Niech ![]() i
i ![]() niezależne zmienne losowe o rozkładzie normalnym
niezależne zmienne losowe o rozkładzie normalnym
Niech ![]() , zatem
, zatem ![]() też ma rozkład normalny
też ma rozkład normalny
Okazuje się, że para ![]() ,
, ![]() jest nadmartyngałem. Otóż z niezależności
jest nadmartyngałem. Otóż z niezależności ![]() od
od ![]() wynika, że
wynika, że
Ponieważ założyliśmy, że ![]() , to
, to
czyli
Aby zakończyć dowód, wystarczy zauważyć, że ![]() ma taki sam rozkład jak
ma taki sam rozkład jak ![]() ,
a
,
a ![]() jak
jak ![]() .
.
14.3. Dochód i ryzyko
14.3.1. Oczekiwany dochód i miary ryzyka
Strategie oparte na dominacji stochastycznej wymagają dokładnej znajomości całego rozkładu, co jest:
a) pracochłonne;
b) kosztowne;
c) czasami niewykonalne.
Ponadto prowadzą one do optymalizacji ,,![]() -kryterialnej”.
Dlatego bardziej popularne są strategie oparte na dwu kryteriach:
prognozowany dochód i ryzyko. Maksymalizujemy prognozowany dochód i minimalizujemy ryzyko.
Prowadzi to do następującego kryterium wyboru inwestycji.
-kryterialnej”.
Dlatego bardziej popularne są strategie oparte na dwu kryteriach:
prognozowany dochód i ryzyko. Maksymalizujemy prognozowany dochód i minimalizujemy ryzyko.
Prowadzi to do następującego kryterium wyboru inwestycji.
Niech zmienne losowe ![]() i
i ![]() modelują zysk z dwu inwestycji wymagających
tych samych nakładów. Załóżmy, że mają one różne prognozy dochodu lub różne miary ryzyka.
Oczywistym jest, że jeśli prognozowany dochód dla
modelują zysk z dwu inwestycji wymagających
tych samych nakładów. Załóżmy, że mają one różne prognozy dochodu lub różne miary ryzyka.
Oczywistym jest, że jeśli prognozowany dochód dla ![]() jest większy lub równy prognozowanemu dochodowi dla
jest większy lub równy prognozowanemu dochodowi dla ![]() i
ryzyko dla
i
ryzyko dla ![]() jest mniejsze lub równe ryzyku dla
jest mniejsze lub równe ryzyku dla ![]() , to inwestor wybierze
, to inwestor wybierze ![]() .
.
Jako prognozę dochodu najczęściej przyjmuje się wartość oczekiwaną ![]() , rzadziej medianę
, rzadziej medianę ![]() .
W obu przypadkach jest to prognoza punktowa zysku. Im większa wartość prognozy, tym
inwestycja jest korzystniejsza.
Ale
.
W obu przypadkach jest to prognoza punktowa zysku. Im większa wartość prognozy, tym
inwestycja jest korzystniejsza.
Ale ![]() jest przecież zmienną losową i należy uwzględnić, że wynik może być różny od prognozy.
Dlatego wprowadza się pojęcie ryzyka. Ma ono w analizie portfelowej dwa znaczenia.
jest przecież zmienną losową i należy uwzględnić, że wynik może być różny od prognozy.
Dlatego wprowadza się pojęcie ryzyka. Ma ono w analizie portfelowej dwa znaczenia.
1. Możliwość wystąpienia efektu niezgodnego z przewidywaniami. Nieważne, czy jest to
przykra niespodzianka, czy przyjemne zaskoczenie; ważne, że prognoza była niedokładna.
2. Możliwość poniesienia straty. Uwzględniamy tylko przykre niespodzianki.
Najbardziej popularne miary ryzyka to:
![]() dla niezgodności z przewidywaniami (1.).
dla niezgodności z przewidywaniami (1.).
Odchylenie standardowe i wariancja.
wyznaczamy prognozę błędu prognozy.
![]() dla możliwości straty (2.).
dla możliwości straty (2.).
Ujemne semiodchylenie standardowe
i ujemna semiwariancja.
![]() i
i ![]() , to odpowiedniki odchylenia standardowego i wariancji w przypadku drugiej interpretacji ryzyka.
, to odpowiedniki odchylenia standardowego i wariancji w przypadku drugiej interpretacji ryzyka.
![]() dla obu interpretacji ryzyka (1. i 2.).
dla obu interpretacji ryzyka (1. i 2.).
Odchylenie przeciętne i ujemne semiodchylenie przeciętne.
Ponieważ ![]() (lemat 14.3) to
można je stosować przy obu interpretacjach ryzyka,
mierzą one zarówno błąd prognozy, jak i wielkość możliwej straty.
(lemat 14.3) to
można je stosować przy obu interpretacjach ryzyka,
mierzą one zarówno błąd prognozy, jak i wielkość możliwej straty.
Zauważmy, że w przypadku rozkładu normalnego powyższe miary są równoważne, w szczególności
odchylenie standardowe, semiodchylenie standardowe, odchylenie przeciętne i semiodchylenie przeciętne
są proporcjonalne. Rzeczywiście, jeśli ![]() ma rozkład normalny o parametrach
ma rozkład normalny o parametrach ![]() i
i ![]() ,
, ![]() ,
to (por. ćwiczenie 14.2)
,
to (por. ćwiczenie 14.2)
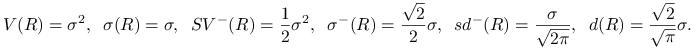 |
14.3.2. Model Markowitza
Przyjęcie wartości oczekiwanej jako miary dochodowości, a odchylenia standardowego jako miary ryzyka jest równoważne stwierdzeniu, że inwestor dokonuje wyboru inwestycji zgodnie z relacją (kryterium) Markowitza ([28, 29]).
Definicja 14.6
Relacja Markowitza jest określona tylko dla zmiennych losowych o skończonych zarówno wartości oczekiwanej,
jak i wariancji (![]() ).
W przypadku zmiennych losowych o rozkładzie normalnym relacja Markowitza jest zgodna z drugą dominacją stochastyczną.
Natomiast w przypadku zmiennych losowych o rozkładach w znaczny sposób różniących się od
rozkładu normalnego (np. dyskretnych) należy przy jej stosowaniu zachować dużą ostrożność. Zilustrujemy to
następującym przykładem.
).
W przypadku zmiennych losowych o rozkładzie normalnym relacja Markowitza jest zgodna z drugą dominacją stochastyczną.
Natomiast w przypadku zmiennych losowych o rozkładach w znaczny sposób różniących się od
rozkładu normalnego (np. dyskretnych) należy przy jej stosowaniu zachować dużą ostrożność. Zilustrujemy to
następującym przykładem.
Przykład
Rozważmy dwie inwestycje, które wymagają takich samych nakładów i rozliczenie, których nastąpi w tym samym czasie.
Wiadomo, że wypłata z pierwszej wyniesie 3 tys. zł, a z drugiej z tym samym prawdopodobieństwem (50%)
3 lub 4 tys. zł. Oczywiste jest, że każdy racjonalny inwestor wybierze drugą inwestycję. Niemniej
zauważmy, że
Zatem ![]() , podczas gdy
, podczas gdy
co oznacza, że z punktu widzenia kryterium Markowitza inwestycje ![]() i
i ![]() są nieporównywalne.
są nieporównywalne.
Zauważmy, że relacja Markowitza zachowuje się przy przeskalowaniu.
Lemat 14.6
Niech ![]() ,
, ![]() , wówczas
, wówczas
Dowód.
Wartość oczekiwana jest liniowa, a odchylenie standardowe dodatnio jednorodne, zatem
Wobec tego
Zatem obie nierówności zostają zachowane przy przeskalowaniu.
Wniosek 14.9
Niech ![]() wypłaty,
wypłaty, ![]() zysk, a
zysk, a ![]() stopy zwrotu
z dwóch inwestycji, które wymagają tych samych nakładów
stopy zwrotu
z dwóch inwestycji, które wymagają tych samych nakładów ![]() . Wówczas następujące warunki są równoważne
. Wówczas następujące warunki są równoważne
i. ![]() ,
,
ii. ![]() ,
,
iii. ![]() .
.
Kryterium Markowitza jest powszechnie używane przy planowaniu składu portfela inwestycyjnego.
Założenia modelowe.
Inwestor inwestuje kwotę ![]() ,
, ![]() w portfel inwestycyjny, który może zawierać
w portfel inwestycyjny, który może zawierać ![]() papierów wartościowych.
Oznaczmy przez
papierów wartościowych.
Oznaczmy przez ![]() stopę zwrotu z
stopę zwrotu z ![]() -tego papieru, a przez
-tego papieru, a przez ![]() kwotę zainwestowaną w ten papier
(
kwotę zainwestowaną w ten papier
(![]() ).
). ![]() są znane w momencie zawarcia transakcji, a
są znane w momencie zawarcia transakcji, a ![]() modelujemy jako zmienne losowe
o skończonej wariancji.
Zysk i stopa zwrotu z portfela wynoszą
modelujemy jako zmienne losowe
o skończonej wariancji.
Zysk i stopa zwrotu z portfela wynoszą
Oznaczmy przez ![]() udział
udział ![]() -tego waloru w portfelu
-tego waloru w portfelu
Wówczas wzór na stopę zwrotu przyjmuje postać
Wartość oczekiwana stopy zwrotu z portfela jest kombinacją liniową stóp zwrotu z poszczególnych papierów
a wariancja kombinacją liniową ich wariancji i kowariancji ([21] §5.6 Twierdzenie 16)
Biorąc pod uwagę, że ![]() i
i ![]() , możemy
zapisać powyższy wzór jako podwójną sumę
, możemy
zapisać powyższy wzór jako podwójną sumę
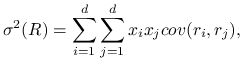 |
lub w postaci macierzowej
![\sigma^{2}(R)=x^{T}Cx,\;\;\mbox{ gdzie }\;\; x=\left(\begin{array}[]{c}x_{1}\\
\dots\\
x_{d}\\
\end{array}\right),\;\;\; C=\left(cov(r_{i},r_{j})\right)_{{i,j=1,\dots,d}}\;.](wyklady/rka/mi/mi1699.png) |
Zbiór inwestycji dopuszczalnych ![]() opisujemy jako podzbiór
opisujemy jako podzbiór ![]() .
Punkt
.
Punkt ![]() należy do
należy do ![]() wtedy i tylko wtedy, gdy inwestor może zainwestować w portfel
o składzie
wtedy i tylko wtedy, gdy inwestor może zainwestować w portfel
o składzie ![]() .
Na ogół przyjmuje się, że wszystkie aktywa są nieskończenie podzielne i
.
Na ogół przyjmuje się, że wszystkie aktywa są nieskończenie podzielne i ![]() jest podzbiorem wypukłym
hiperpłaszczyzny
jest podzbiorem wypukłym
hiperpłaszczyzny ![]() .
.
Odwzorowanie, które przyporządkowuje portfelowi o składzie ![]() odchylenie standardowe jego stopy zwrotu
odchylenie standardowe jego stopy zwrotu ![]() i jej wartość oczekiwaną
i jej wartość oczekiwaną ![]() , nazywa się
odwzorowaniem Markowitza
, nazywa się
odwzorowaniem Markowitza
Obraz ![]() nazywa się zbiorem możliwości.
Portfel o składzie
nazywa się zbiorem możliwości.
Portfel o składzie ![]() ,
, ![]() , nazywamy efektywnym, gdy stopa zwrotu z tego portfela
, nazywamy efektywnym, gdy stopa zwrotu z tego portfela ![]() jest
maksymalna względem relacji Markowitza
jest
maksymalna względem relacji Markowitza
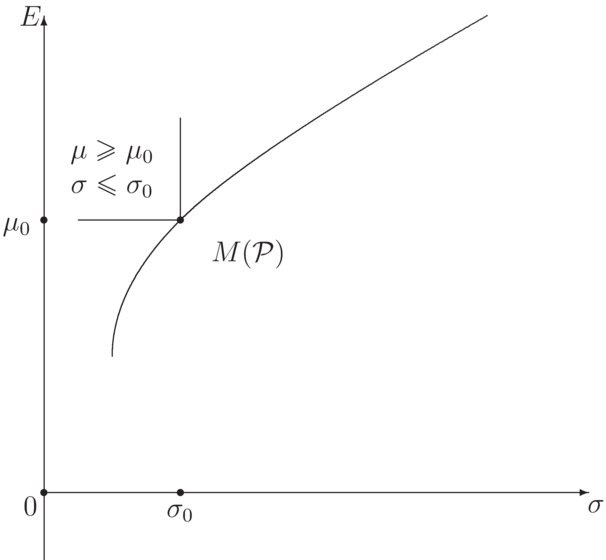
Obraz zbioru portfeli efektywnych jest zawarty w brzegu zbioru możliwości i nazywa się
granicą efektywną (rys. 5.2). Zauważmy, że ma ona prostą interpretację geometryczną.
Punkt ![]() należy do granicy efektywnej, gdy
zbiór możliwości i zbiór punktów leżących na lewo i powyżej punktu
należy do granicy efektywnej, gdy
zbiór możliwości i zbiór punktów leżących na lewo i powyżej punktu ![]() przecinają się tylko w tym punkcie
przecinają się tylko w tym punkcie
14.4. Ćwiczenia
Ćwiczenie 14.1
Oszacowano następujące prawdopodobieństwa wypłat dla inwestycji A, B i C:
Inwestycja A:
| wypłata [tys. zł] | 6 | 8 | 10 | 13 | 15 |
| prawdopodobieństwo [%] | 20 | 10 | 15 | 25 | 30 |
Inwestycja B:
| wypłata [tys. zł] | 6 | 7 | 9 | 10 | 11 | 14 | 15 | 16 |
| prawdopodobieństwo [%] | 15 | 5 | 5 | 15 | 5 | 25 | 20 | 10 |
Inwestycja C:
| wypłata [tys. zł] | 6 | 7 | 8 | 9 | 11 | 13 | 14 | 15 |
| prawdopodobieństwo [%] | 10 | 5 | 10 | 5 | 15 | 10 | 25 | 20 |
Sprawdzić, czy na podstawie kryterium dominacji stochastycznej można wybrać
najlepszą spośród nich (każda wymaga zainwestowania 10 000 zł).
Rozwiązanie.Wypłaty są skokowymi zmiennymi losowymi, zatem ich dystrybuanty (![]() ) są funkcjami schodkowymi, a całki z dystrybuant (
) są funkcjami schodkowymi, a całki z dystrybuant (![]() )
ciągłymi funkcjami kawałkami liniowymi. Aby je scharakteryzować, wystarczy wyznaczyć ich wartości na
dyskretnym zbiorze punktów zawierającym wszystkie wartości, jakie mogą przyjmować z niezerowym prawdopodobieństwem
wypłaty
)
ciągłymi funkcjami kawałkami liniowymi. Aby je scharakteryzować, wystarczy wyznaczyć ich wartości na
dyskretnym zbiorze punktów zawierającym wszystkie wartości, jakie mogą przyjmować z niezerowym prawdopodobieństwem
wypłaty ![]() ,
, ![]() i
i ![]() . Wielkości te są przedstawione w poniższej tabelce.
. Wielkości te są przedstawione w poniższej tabelce.
| K | 6 | 7 | 8 | 9 | 10 | 11 | 13 | 14 | 15 | 16 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 20 | 0 | 10 | 0 | 15 | 0 | 25 | 0 | 30 | 0 | |
| P(K) | B | 15 | 5 | 0 | 5 | 15 | 5 | 0 | 25 | 20 | 10 |
| C | 10 | 5 | 10 | 5 | 0 | 15 | 10 | 25 | 20 | 0 | |
| A | 20 | 20 | 30 | 30 | 45 | 45 | 70 | 70 | 100 | 100 | |
| F | B | 15 | 20 | 20 | 25 | 40 | 45 | 45 | 70 | 90 | 100 |
| C | 10 | 15 | 25 | 30 | 30 | 45 | 55 | 80 | 100 | 100 | |
| A | 0 | 20 | 40 | 70 | 100 | 145 | 235 | 305 | 375 | 475 | |
| G | B | 0 | 15 | 35 | 55 | 80 | 120 | 210 | 255 | 325 | 415 |
| C | 0 | 10 | 25 | 50 | 80 | 110 | 200 | 255 | 335 | 435 |
Wiersz ![]() zawiera wszystkie możliwe wartości wypłat. W następnych trzech wierszach podane są prawdopodobieństwa,
z jakimi są one przyjmowane odpowiednio przez
zawiera wszystkie możliwe wartości wypłat. W następnych trzech wierszach podane są prawdopodobieństwa,
z jakimi są one przyjmowane odpowiednio przez ![]() ,
, ![]() i
i ![]() . Poniżej są wartości dystrybuant,
a pod nimi całek z dystrybuant.
Zauważmy, że wartości dystrybuant
. Poniżej są wartości dystrybuant,
a pod nimi całek z dystrybuant.
Zauważmy, że wartości dystrybuant ![]() i całek
i całek ![]() oblicza się rekurencyjnie według następujących wzorów:
oblicza się rekurencyjnie według następujących wzorów:
Na podstawie tabelki stwierdzamy, że w każdym punkcie dystrybuanta ![]() przyjmuje wartości większe niż
dystrybuanta
przyjmuje wartości większe niż
dystrybuanta ![]() bądź równe.
Nie jest to prawdą dla pozostałych par dystrybuant
bądź równe.
Nie jest to prawdą dla pozostałych par dystrybuant ![]() i
i ![]() oraz
oraz ![]() i
i ![]() . Zatem
. Zatem ![]() , a
, a ![]() jest
jest ![]() -nieporównywalne z
-nieporównywalne z ![]() i
i ![]() .
.
Całki ![]() mierzą pola pod wykresami dystrybuant, zatem
mierzą pola pod wykresami dystrybuant, zatem ![]() przyjmuje nie mniejsze wartości niż
przyjmuje nie mniejsze wartości niż ![]() .
Z tabelki otrzymujemy, że również wykres
.
Z tabelki otrzymujemy, że również wykres ![]() leży poniżej wykresu
leży poniżej wykresu ![]() . Natomiast wykresy
. Natomiast wykresy ![]() i
i ![]() przecinają się.
Zatem
przecinają się.
Zatem ![]() i
i ![]() , ale
, ale ![]() jest
jest ![]() -nieporównywalne z
-nieporównywalne z ![]() .
.
Odpowiedź.
Inwestor dokonujący wyboru inwestycji na podstawie dominacji stochastycznej pierwszego lub drugiego rzędu
powinien odrzucić inwestycję ![]() . Inwestycje
. Inwestycje ![]() i
i ![]() są nieporównywalne względem
obu dominacji. Zatem kryteria oparte na pierwszej i drugiej dominacji stochastycznej nie dają wskazówek,
którą z inwestycji należy wybrać.
są nieporównywalne względem
obu dominacji. Zatem kryteria oparte na pierwszej i drugiej dominacji stochastycznej nie dają wskazówek,
którą z inwestycji należy wybrać.
Ćwiczenie 14.2
Wyznaczyć ujemne semiodchylenie przeciętne dla zmiennej losowej ![]() o rozkładzie
o rozkładzie ![]() .
.
Rozwiązanie.
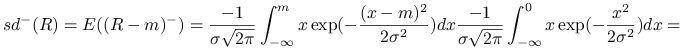 |
Odpowiedź.
Ujemne semiodchylenie przeciętne dla zmiennej losowej ![]() o rozkładzie
o rozkładzie ![]() wynosi
wynosi
![]() .
.
Ćwiczenie 14.3
W oparciu o relację Markowitza
określić, która z poniższych inwestycji jest bardziej, a która mniej korzystna:
inwestycja A – stopa zwrotu ma rozkład ![]() ;
;
inwestycja B – stopa zwrotu ma rozkład ![]() ;
;
inwestycja C – stopa zwrotu ma rozkład ![]() .
.
Rozwiązanie.Porównujemy wartości oczekiwane i odchylenia standardowe
Zatem inwestycja B ma największą wartość oczekiwaną stopy zwrotu i najmniejsze odchylenie standardowe, czyli
Natomiast stopy zwrotu z inwestycji A i C są nieporównywalne względem relacji Markowitza,
A ma lepsze odchylenie standardowe, a C wartość oczekiwaną.
Odpowiedź.
Zgodnie z relacją Markowitza najkorzystniejsza jest inwestycja B. Pozostałe dwie inwestycje
są nieporównywalne względem relacji Markowitza, a tym samym nie daje ona wskazówek, która z nich jest bardziej,
a która mniej korzystna.