Zagadnienia
9. Giełda. Rynek akcji
Liczba godzin 8.
Zakres materiału:
Giełda. Sposób działania, wyznaczanie kursu. Systemy notowań. Notowania ciągłe, cena otwarcia, cena zamknięcia. Indeksy giełdowe. Specyfika rynku akcji. Analiza techniczna i fundamentalna. Ryzyko. Akcje = własność firmy. Dywidenda, walne zgromadzenia akcjonariuszy. Krótka sprzedaż. Izby rozliczeniowe. Granie na spadkach. Kontrakty forward i futures. Opcje. Pojęcie arbitrażu. Wycena arbitrażowa.
9.1. Giełdy, notowane instrumenty
Giełdy stanowią specyficzną formę wymiany towarów i zawierania transakcji. W zależności od rodzaju towarów wyróżnia się:
– giełdy towarowe (np. energii elektrycznej, produktów rolnych, surowców itp.),
– giełdy terminowe,
– giełdy papierów wartościowych.
Funkcjonowanie giełdy papierów wartościowych opiszemy na przykładzie Giełdy Papierów Wartościowych
w Warszawie, gdzie
notowane są następujące
papiery wartościowe: akcje, prawa do akcji, prawa poboru, obligacje,
certyfikaty inwestycyjne oraz instrumenty pochodne:
futures, opcje
i jednostki indeksowe.
Zacznijmy od ich krótkiej charakterystyki.
9.1.1. Akcje
Akcja (stock, share), to dokument stwierdzający udział jej posiadacza, czyli akcjonariusza,
w majątku spółki akcyjnej. Akcjonariusz ma zapewnione:![]() prawo do dywidend;
prawo do dywidend;![]() prawo do uczestnictwa w walnym zgromadzeniu akcjonariuszy;
prawo do uczestnictwa w walnym zgromadzeniu akcjonariuszy;![]() prawo do udziału w majątku spółki w przypadku jej likwidacji.
prawo do udziału w majątku spółki w przypadku jej likwidacji.
Akcje dzielimy na zwykłe i uprzywilejowane. Uprzywilejowanie zazwyczaj dotyczy:![]() głosu na zebraniu akcjonariuszy,
głosu na zebraniu akcjonariuszy,![]() pierwszeństwa w wypłacaniu dywidendy,
pierwszeństwa w wypłacaniu dywidendy,![]() pierwszeństwa w podziale majątku spółki w przypadku jej likwidacji.
pierwszeństwa w podziale majątku spółki w przypadku jej likwidacji.
Na giełdzie inwestor może zakupić akcje dopuszczone do obrotu giełdowego, sprzedać posiadane
akcje i dokonać krótkiej sprzedaży akcji.
9.1.2. Krótka sprzedaż
Krótką sprzedażą nazywamy sprzedaż aktywów, których się nie posiada (tzn. nie ma w swoim portfelu inwestycyjnym), w celu ich późniejszego odkupienia.
Na giełdzie warszawskiej transakcja ta interpretowana jest jako rodzaj pożyczki i
podlega regulacjom prawnym
zgodnie z Rozporządzeniem Rady Ministrów z 21 grudnia 1999
(Dz.U.99.110.1269).
Istotą krótkiej sprzedaży jest zarabianie na spadkach kursów papierów wartościowych, i to takich papierów,
których nie mamy w swoim portfelu inwestycyjnym.
Aby dokonać krótkiej sprzedaży, należy najpierw pożyczyć papiery wartościowe od biura maklerskiego.
Zwykle wymaga to wpłacenia depozytu proporcjonalnego do kwoty pożyczki.
Inwestor pożycza określoną liczbę akcji, spodziewając się spadku ich ceny.
Jednocześnie zobowiązuje się zwrócić je w określonym terminie, po odkupieniu na giełdzie.
Jeżeli kurs danych papierów faktycznie spadnie,
odkupienie ich po niższym kursie oznaczać będzie zarobek na różnicy między ceną sprzedaży (gdy kurs był wyższy)
a ceną odkupu papierów (gdy kurs był niższy). Oczywiście zysk inwestora zostanie pomniejszony o koszty
transakcyjne, koszty pożyczki i koszt utrzymania depozytu.
Transakcje krótkiej sprzedaży podlegają licznym ograniczeniom. Na niektórych rynkach
transakcji krótkiej sprzedaży nie można dokonać, gdy kurs danego
papieru wartościowego spada. Obowiązują zasady:
a) up-tick rule (tik w górę), która mówi, że transakcja
krótkiej sprzedaży może być dokonana po cenie wyższej od ceny
poprzedniej transakcji lub
b)zero-plus tick, mówiąca o tym, że transakcja krótkiej sprzedaży
może być dokonana po cenie równej cenie transakcji poprzedniej, ale
wyższej od ceny ostatniej transakcji dokonanej po cenie różnej od
mającej nastąpić transakcji krótkiej sprzedaży.
9.1.3. Prawa poboru i prawa do akcji
Gdy spółka akcyjna potrzebuje kapitału na nowe przedsięwzięcia lub na
pokrycie strat i przedłużenie działalności walne zgromadzenie
akcjonariuszy może uchwalić nową emisję akcji,
albo![]() z prawem poboru nowych akcji,
czyli pozwalającą zachować procentowe udziały w kapitale spółki
dotychczasowym akcjonariuszom, albo
z prawem poboru nowych akcji,
czyli pozwalającą zachować procentowe udziały w kapitale spółki
dotychczasowym akcjonariuszom, albo![]() z wyłączeniem prawa poboru, gdy potrzeby firmy i możliwości finansowe
akcjonariuszy skłaniają uczestników walnego zgromadzenia do wyłączenia
dotychczasowych akcjonariuszy z prawa poboru. Wówczas emisja
kierowana jest do wybranego grona inwestorów, czy też emisja jest publiczna.
z wyłączeniem prawa poboru, gdy potrzeby firmy i możliwości finansowe
akcjonariuszy skłaniają uczestników walnego zgromadzenia do wyłączenia
dotychczasowych akcjonariuszy z prawa poboru. Wówczas emisja
kierowana jest do wybranego grona inwestorów, czy też emisja jest publiczna.
Prawo poboru nowych akcji (PPA)
Prawo to ma zastosowanie do nowej emisji akcji przez spółkę.
Oznacza ono przywilej pierwszeństwa przy zakupie nowych akcji przez dotychczasowych akcjonariuszy.
Prawo to jest o tyle istotne, że w przypadku objęcia (zakupu) takiej emisji przez nowy krąg akcjonariuszy nastąpiłoby tzw.
rozwodnienie kapitału, czyli procentowe zmniejszenie udziału dotychczasowych akcjonariuszy w stosunku
do całkowitej sumy kapitału akcyjnego.
Na mocy prawa poboru, aktualni akcjonariusze mają możliwość zachowania dotychczasowego stanu posiadania w spółce akcyjnej.
Ważną cechą prawa poboru jest to, że może być przedmiotem obrotu jako samodzielny papier wartościowy.
Dotychczasowi posiadacze starych akcji mogą zrezygnować z prawa objęcia nowych akcji, sprzedając
to prawo na giełdzie.
Jednocześnie ci, którzy chcieliby nabyć akcje nowej emisji spółki, a przedtem nie byli jej akcjonariuszami,
kupując prawa poboru mają taką możliwość.
Prawa do akcji (PDA)
Inwestorzy, którym przydzielono akcje nowej emisji oferowane w publicznej subskrypcji nie mogą ich sprzedać przed faktycznym otrzymaniem. Z kolei wydanie akcji nabywcom, zgodnie z kodeksem handlowym, następuje dopiero po sądowej rejestracji papierów. Następne działania to obowiązkowa rejestracja akcji w Krajowym Depozycie Papierów Wartościowych oraz doprowadzenie do notowania ich na giełdzie.
Cała procedura trwa często kilka tygodni, co mogłoby zniechęcić wielu potencjalnych inwestorów do zakupu akcji nowej emisji.
Aby jeszcze przed pierwszym notowaniem akcji stworzyć możliwość wycofania się z dokonanej inwestycji tym,
którym przydzielono nowe akcje, i jednocześnie dać możliwość ich nabycia tym,
którzy nie dokonali tego w publicznej subskrypcji,
GPW wprowadziła do obrotu giełdowego nowy na polskim rynku kapitałowym
instrument finansowy – prawo do nowych akcji.
9.1.4. Obligacje
Krótka informacja o obligacjach znajduje się w podrozdziale 4.3.
9.1.5. Certyfikaty inwestycyjne
Certyfikaty inwestycyjne, to papiery wartościowe emitowane przez zamknięte fundusze inwestycyjne. Ponieważ są papierami wartościowymi na okaziciela mogą być notowane na giełdzie. Tak jak inne papiery wartościowe notowane na giełdzie podlegają codziennej wycenie rynkowej na sesjach giełdowych. Innym rodzajem wyceny certyfikatów inwestycyjnych jest ta, której cyklicznie dokonuje ich emitent. Wycena dokonywana jest z częstotliwością określoną w statucie, lecz nie rzadziej niż raz na 3 miesiące, a jej podstawę stanowi oszacowanie wartości instrumentów finansowych, w które zainwestował fundusz. A trzeba dodać, że paleta tych instrumentów jest znacznie większa niż w przypadku funduszy otwartych. Zamknięte fundusze inwestycyjne mogą inwestować m.in. w transakcje terminowe, prawa pochodne, waluty, a nawet udziały spółek z o.o., a więc lokaty niedostępne z mocy prawa dla funduszy otwartych. Możliwość inwestowania w instrumenty pochodne stwarza funduszom znacznie większe możliwości tworzenia zróżnicowanych strategii inwestycyjnych.
9.1.6. Kontrakty terminowe futures
Charakterystyka kontraktów terminowych znajduje się w podrozdziale 12.1.2.
9.1.7. Opcje
Opcje będą omówione w podrozdziale 12.1.4.
9.1.8. Produkty strukturyzowane
W dniu 25 sierpnia 2006 r. w obrocie giełdowym pojawiły się nowe instrumenty - tzw. produkty strukturyzowane. Jako pierwsze do obrotu wprowadzone zostały obligacje strukturyzowane Deutsche Bank z Londynu.
Produkty strukturyzowane, to instrumenty finansowe, stanowiące połączenie obligacji zerokuponowej i opcji, z której wypłata jest uzależniona od wartości określonego wskaźnika rynkowego (np. kursu akcji lub koszyków akcji, wartości indeksów giełdowych, kursów walut). Emitentami produktów strukturyzowanych są instytucje finansowe, najczęściej banki lub domy maklerskie, które zobowiązują się wobec nabywcy (inwestora), do wypłaty w terminie wykupu instrumentu kwoty rozliczenia kalkulowanej wg określonego wzoru.
9.1.9. Jednostki indeksowe
Jednostki indeksowe na indeks giełdowy WIG20
są instrumentami pochodnymi
w rozumieniu art.
3 ust. 3 Ustawy z dnia 21 sierpnia 1997 r. Prawo o publicznym obrocie papierami
wartościowymi (Dz.U. z 1997 r. Nr 118 poz. 754 z późn. zm.).
Zgodnie z tym aktem prawnym jednostki indeksowe na indeks giełdowy WIG20 (tzw. MiniWIG20) są
papierami wartościowymi (oznaczenie kodowe MW20).
Jednostka indeksowa, to
prawo, przysługujące nabywcy jednostki
wobec wystawcy, do żądania zapłaty kwoty należnej na warunkach określonych w standardzie
jednostek indeksowych na indeks giełdowy WIG20.
Nabywca jednostki indeksowej płaci jej wystawcy cenę jednostki indeksowej (premię).
Wystawca otwierający krótkie pozycje (a więc dokonujący krótkiej sprzedaży)
wnosi depozyty zabezpieczające do KDPW.
Nabywca jednostek indeksowych nie musi wnosić ani utrzymywać depozytów
zabezpieczających.
Wartość jednej jednostki indeksowej odpowiada wartości indeksu giełdowego WIG20
pomnożonej przez mnożnik wynoszący 0,1 zł.
Po nabyciu inwestor może do ostatniego dnia obrotu włącznie zamknąć swoją pozycję na dwa
sposoby:![]() poprzez sprzedaż (wystawienie) jednostki indeksowej.
poprzez sprzedaż (wystawienie) jednostki indeksowej.![]() poprzez wykonanie jednostki indeksowej.
poprzez wykonanie jednostki indeksowej.
Wykonanie jednostek indeksowych odbywa się w oparciu o cenę rozliczeniową równą, wartości otwarcia instrumentu bazowego (indeksu WIG20) ustalonej w pierwszym dniu sesyjnym po wykonaniu jednostki indeksowej pomnożonej przez mnożnik 0,1 zł. Nabywca (inwestor posiadający pozycję długą) ma prawo zgłosić jednostkę do wykonania w dowolnym terminie do dnia poprzedzającego ostatni dzień obrotu – może zażądać wypłaty kwoty należnej równej kwocie rozliczeniowej jednostki indeksowej. Wystawca jednostki indeksowej (inwestor posiadający pozycję krótką), który zostanie wybrany w celu wykonania jednostki, jest zobowiązany do wypłacenia nabywcy kwoty równej kwocie rozliczenia jednostki indeksowej. Wykonanie w ostatnim dniu obrotu (dniu poprzedzającym dzień wygaśnięcia) następuje automatycznie chyba, że posiadacz jednostki zgłosi rezygnację z wykonania jednostki. Dzień wygaśnięcia jednostek indeksowych objętych niniejszymi warunkami przypada na ostatni dzień sesyjny grudnia 2025 r. Po wystawieniu inwestor może zamknąć swoją pozycję poprzez nabycie jednostki indeksowej. Wystawca jednostek indeksowych w momencie zawierania transakcji zobowiązany jest wpłacić depozyt zabezpieczający na zasadach określonych przez KDPW. Zobowiązany jest on również do aktualizowania swoich depozytów na zasadach określonych przez KDPW. Podstawę do wyznaczania depozytów zabezpieczających stanowi kurs odniesienia.
9.2. Giełda Papierów Wartościowych w Warszawie
9.2.1. Historia
Pierwsza wersja projektu ustawy regulującej publiczny obrót papierami wartościowymi została opracowana w lipcu 1990 r. W dniu 22 marca 1991 r. Sejm uchwalił ustawę Prawo o publicznym obrocie papierami wartościowymi i funduszach powierniczych. Powstały w ten sposób podwaliny prawne głównych instytucji rynku kapitałowego: domów maklerskich, giełdy, funduszy powierniczych, a także Komisji Papierów Wartościowych jako organu administracji rządowej kontrolującego i promującego rynek papierów wartościowych. Wspomniana ustawa określiła, że giełda powinna zapewniać:![]() koncentrację podaży i popytu na papiery wartościowe dopuszczone do obrotu giełdowego w celu kształtowania powszechnego kursu;
koncentrację podaży i popytu na papiery wartościowe dopuszczone do obrotu giełdowego w celu kształtowania powszechnego kursu;![]() bezpieczny i sprawny przebieg transakcji i rozliczeń;
bezpieczny i sprawny przebieg transakcji i rozliczeń;![]() upowszechnianie jednolitych informacji umożliwiających ocenę aktualnej wartości papierów wartościowych dopuszczonych do obrotu giełdowego.
upowszechnianie jednolitych informacji umożliwiających ocenę aktualnej wartości papierów wartościowych dopuszczonych do obrotu giełdowego.
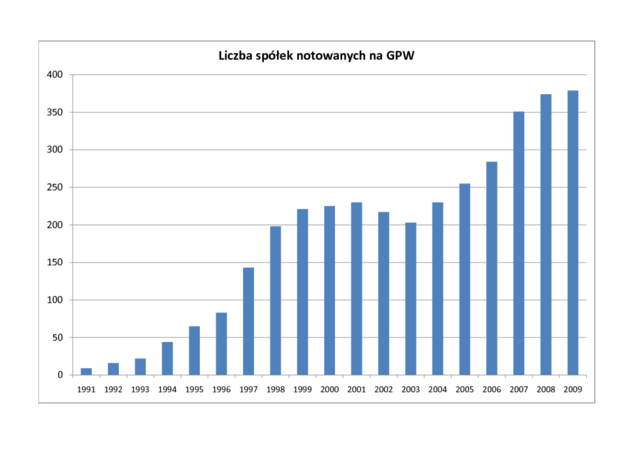
Niecały miesiąc po uchwaleniu przez Sejm Prawa o publicznym obrocie papierami wartościowymi i funduszach powierniczych, dnia 12 kwietnia 1991 roku, Minister Przekształceń Własnościowych i Minister Finansów reprezentujący Skarb Państwa podpisali akt założycielski Giełdy Papierów Wartościowych w Warszawie. Cztery dni później, 16 kwietnia 1991 roku odbyła się pierwsza sesja giełdowa, z udziałem 7 domów maklerskich, na której notowano akcje 5 spółek. Wpłynęło wówczas 112 zleceń kupna i sprzedaży, a łączny obrót giełdy wyniósł 1.990 zł (2 tys. USD).
Obecnie Giełda Papierów Wartościowych w Warszawie działa w oparciu o ustawy z dnia 29 lipca 2005 r.:
O ofercie publicznej i warunkach wprowadzania instrumentów finansowych do zorganizowanego systemu obrotu oraz o spółkach publicznych (z pózn. zm.);
O obrocie instrumentami finansowymi (z pózn. zm.);
O nadzorze nad rynkiem kapitałowym (z pózn. zm.).
9.2.2. Struktura
Rynki notowań
Obrót instrumentami finansowymi na Giełdzie Papierów Wartościowych odbywa się na jednym z dwóch rynków: podstawowym lub równoległym, w zależności od spełnienia kryteriów określonych Regulaminem Giełdy.
Przynależność do danego rynku zależy od wielkości spółki i wiąże się z obowiązkiem składania mniej lub bardziej obszernych sprawozdań (raportów) z wyników finansowych spółki.
| Spółki krajowe | Spółki zagraniczne | Razem | |
|---|---|---|---|
| Rynek podstawowy | 315 | 24 | 339 |
| Rynek równoległy | 39 | 0 | 39 |
| RAZEM | 354 | 24 | 378 |
| Spółki krajowe | Spółki zagraniczne | Razem | |
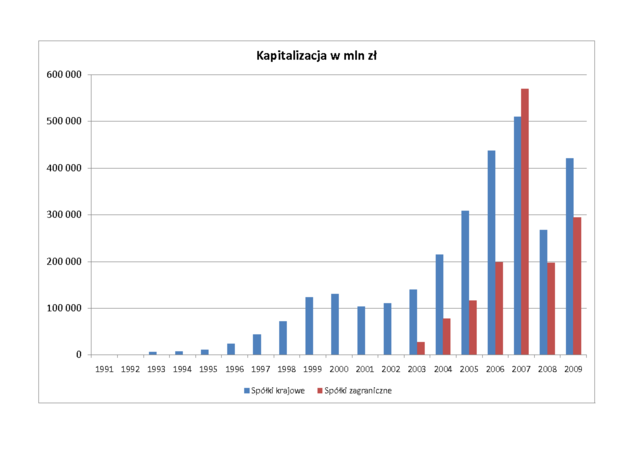
| Rynek podstawowy | 433625,58 | 298404,18 | 732029,76 |
| Rynek równoległy | 3194,59 | 0 | 3194,59 |
| RAZEM | 436820,17 | 298404,18 | 735224,35 |
Segmenty rynku
Wszystkie spółki przydzielone są do jednego z czterech poniższych segmentów rynku:
Segment 250 PLUS - akcje spółek o kapitalizacji przekraczającej 250 mln euro;
Segment 50 PLUS - akcje spółek o kapitalizacji od 50 do 250 mln euro;
Segment 5 PLUS - akcje spółek, których kapitalizacja nie przekracza 50 mln euro;
Segment MINUS 5 - akcje spółek, których kapitalizacja nie przekracza 5 mln euro.
Akcje spółek, których kurs charakteryzuje się wysoką zmiennością lub są w stanie upadłości mogą należeć do segmentu LISTA ALERTÓW i wtedy są notowane w systemie kursu jednolitego.
Akcji spółek z segmentów MINUS 5 oraz LISTA ALERTÓW nie uwzględnia się przy ustalaniu indeksów giełdowych.
Sektory gospodarki reprezentowane na Giełdzie
Giełda klasyfikuje spółki do
18 sektorów gospodarki narodowej,
zgrupowanych w trzech głównych działach: przemysł, finanse i usługi.
Przemysł:
-
spożywczy,
-
lekki,
-
drzewny,
-
chemiczny,
-
farmaceutyczny,
-
tworzyw sztucznych,
-
paliwowy,
-
materiałów budowlanych,
-
budownictwo,
-
elektromaszynowy,
-
metalowy,
-
motoryzacyjny,
-
inne.
Finanse:
-
banki,
-
ubezpieczenia,
-
deweloperzy,
-
inne.
Usługi:
-
handel hurtowy,
-
handel detaliczny,
-
konglomeraty,
-
informatyka,
-
telekomunikacja,
-
media,
-
energetyka,
-
hotele i restauracje,
-
inne.
Podział ten umożliwia obliczanie wskaźników sektorowych dla poszczególnych branż reprezentowanych
na Giełdzie i łatwe śledzenie koniunktury panującej w różnych sektorach gospodarki.
Sektory o największym znaczeniu dla obrotu giełdowego i największej reprezentacji spółek
mają swoje indeksy zwane subindeksami sektorowymi.
9.2.3. Systemy notowań
Z punktu widzenia inwestora od przypisania do branży dużo ważniejsze jest, w jakim systemie notowań
następuje obrót akcjami danej spółki. Na GPW w Warszawie mamy system mieszany: częścią papierów
handluje się w systemie ciągłym, a częścią w periodycznym.
Harmonogram notowań
w systemie ciągłym
(akcje) – styczeń 2011
| 8.00-9.00 | Faza przed otwarciem | Przyjmowanie zleceń na otwarcie |
| 9.00 | Otwarcie – fixing (okre- | Realizacja zleceń |
| ślenie kursu otwarcia) | po kursie otwarcia | |
| 9.00-17.20 | Faza notowań ciągłych | Przyjmowanie i realizacja zleceń |
| 17.20-17.30 | Faza przed zamknięciem | Przyjmowanie zleceń |
| na zamknięcie | ||
| 17.30 | Zamknięcie – fixing (okre- | Realizacja zleceń |
| ślenie kursu zamknięcia) | po kursie zamknięcia | |
| 17.30-17.35 | Dogrywka | Przyjmowanie i realizacja zleceń |
| po kursie zamknięcia |
Harmonogram notowań w systemie ciągłym
(instrumenty pochodne) – styczeń 2011
| 8.00-8.30 | Faza przed otwarciem | Przyjmowanie zleceń na otwarcie |
| 8.30 | Otwarcie – fixing (okre- | Realizacja zleceń |
| ślenie kursu otwarcia) | po kursie otwarcia | |
| 8.30-17.20 | Faza notowań ciągłych | Przyjmowanie i realizacja zleceń |
| 17.20-17.30 | Faza przed zamknięciem | Przyjmowanie zleceń |
| na zamknięcie | ||
| 17.30 | Zamknięcie – fixing (okre- | Realizacja zleceń |
| ślenie kursu zamknięcia) | po kursie zamknięcia | |
| 17.30-17.35 | Dogrywka | Przyjmowanie i realizacja zleceń |
| po kursie zamknięcia |
Harmonogram notowań jednolitych (system periodyczny)
– styczeń 2011
| 8.30-11.00 | Faza przed otwarciem | Przyjmowanie zleceń na otwarcie |
| 11.00 | Fixing (określenie | Realizacja zleceń |
| kursu jednolitego) | po kursie jednolitym | |
| 11.00-11.30 | Dogrywka | Przyjmowanie i realizacja zleceń |
| po kursie jednolitym | ||
| 11.30-15.00 | Faza przed otwarciem | Przyjmowanie zleceń na otwarcie |
| 15.00 | Fixing (określenie | Realizacja zleceń |
| kursu jednolitego) | po kursie jednolitym | |
| 15.00-15.30 | Dogrywka | Przyjmowanie i realizacja zleceń |
| po kursie jednolitym | ||
| 15.30-17.35 | Faza przed otwarciem | Przyjmowanie zleceń |
| na otwarcie następnej sesji |
Zlecenia
Inwestorzy składają zlecenia za pośrednictwem swoich biur maklerskich.
Najprostsze zlecenie zawiera następujące dane:![]() informację, czy jest to zlecenie kupna czy sprzedaży,
informację, czy jest to zlecenie kupna czy sprzedaży,![]() termin ważności zlecenia,
termin ważności zlecenia,![]() nazwę papieru wartościowego,
nazwę papieru wartościowego,![]() wielkość transakcji (np. liczba akcji),
wielkość transakcji (np. liczba akcji),![]() limit ceny.
limit ceny.
W przypadku zlecenia kupna jest to najwyższa cena,
a w przypadku zlecenia sprzedaży najniższa, jaką inwestor jest
skłonny zaakceptować.
Zlecenia składane w czasie dogrywki mają limit ceny równy kursowi ustalonemu na fixingu.
Ponadto inwestor może złożyć
zlecenie bez limitu ceny. Na przykład PKC czyli po każdej cenie; PCR po cenie rynkowej i PCRO po cenie rynkowej na otwarcie.
PKC interpretuje się jako zlecenie, w którym limit ceny jest równy opowiednio górnemu lub dolnemu
ograniczeniu wahań kursów.
Fazy sesji giełdowej
Przed otwarciem.
W tej fazie możliwe jest wprowadzanie zleceń do systemu giełdowego.
Zlecenia składane przez inwestorów trafiają bezpośrednio do centralnego
arkusza zleceń, jednakże nie są zawierane transakcje.
Fixing.
Zostaje wyznaczony kurs otwarcia/zamknięcia (notowania ciagłe)
lub kurs jednolity
(notowania jednolite) i następuje
realizacja po tym kursie jedynie tych wprowadzonych wcześniej zleceń, które mogą być zrealizowane.
Notowania ciągłe.
Możliwe jest wprowadzanie zleceń. Transakcje zawierane są na bieżąco, natychmiast po wprowadzeniu zlecenia,
które może być zrealizowane. Zlecenie, które ze względu na limit ceny nie może być zrealizowane, zostaje
umieszczone w arkuszu zleceń.
Dogrywka.
Wszyscy uczestnicy rynku mogą składać zlecenia kupna i sprzedaży po wyznaczonym kursie. Transakcje zawierane są
na bieżąco.
Widełki – ograniczenia wahań kursów
Widełki to popularna nazwa dla maksymalnych wahań kursów wyznaczanych względem
tzw. kursu odniesienia.
Zgodnie z regulaminem Giełdy Warszawskiej (styczeń 2010) mamy następujące ograniczenia:
Notowania ciągłe:
Kurs odniesienia = kurs zamknięcia.
| instrument | dopuszczalna zmiana na otwarciu | dopuszczalna zmiana w trakcie sesji |
|---|---|---|
| akcje |
|
|
| obligacje |
|
|
| jednostki indeksowe |
|
|
Notowania jednolite:
| instrument | dopuszczalna zmiana na fixingu |
|---|---|
| akcje |
|
W uzasadnionych przypadkach przewodniczący sesji
może zmienić powyższe limity. W przypadku notowań ciągłych oznacza to przerwę w realizacji zleceń,
a następnie przesunięcie pasma dopuszczalnych kursów.
Dokładność określania kursów (styczeń 2010)
W zależności od wysokości kursu akcji i obligacji różna jest dokładność,
z jaką papiery wartościowe są notowane na giełdzie.
Kurs akcji podawany jest w złotych.
| kurs akcji w zł | krok notowania w zł | |
| 0,01 | ||
| 0,05 | ||
| 0,1 | ||
| 0,5 |
Kurs obligacji określany jest w procentach ich wartości nominalnej z dokładnością do 0,01 punktu procentowego.
Kurs certyfikatów inwestycyjnych podawany w złotych, krok notowania wynosi 0,01 zł.
Kurs instrumentów strukturyzowanych określany jest:
a) w przypadku wyznaczania kursu w złotych - z dokładnością do 1 grosza,
b) w przypadku wyznaczania kursu w procentach wartości nominalnej -
z dokładnością do 0,01 punktu procentowego.
9.3. Ćwiczenia - renty
Rentą nazywamy ciąg płatności dokonywanych w równych odstępach czasu.
Przyjęte ustalenia.
1. Kwota płatności jest na ogół stała.
2. Renta może być płatna na początku okresu - ”z góry” lub na końcu okresu - ”z dołu”.
3. Liczba płatności może być nieskończona, skończona określona lub skończona, ale nieokreślona
w momencie zawarcia umowy (np. renta dożywotnia, emerytura).
4. W teorii rozpatruje się też renty z ciągłym strumieniem gotówki.
Będziemy wyznaczać wartość obecną renty przy stałej stopie procentowej ![]() i stałej intensywności
i stałej intensywności ![]() (płaska struktura terminowa)
(płaska struktura terminowa)
Ćwiczenie 9.1
Wyznacz wartość obecną
renty płatnej z dołu przez ![]() lat. Wielkość pojedynczej wypłaty wynosi 1 jednostkę.
lat. Wielkość pojedynczej wypłaty wynosi 1 jednostkę.
Rozwiązanie
1 jednostka jest płatna na koniec roku przez ![]() lat.
lat.
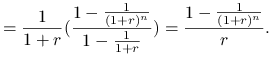 |
Alternatywnie, gdy zastąpimy ![]() przez
przez ![]() , to otrzymamy
, to otrzymamy
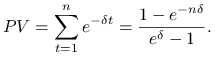 |
Odpowiedź.
Wartość obecna renty wynosi ![]() .
.
Komentarz.
Aktuariusze (”specjaliści od wyznaczania składek ubezpieczeniowych”)
stosują symbol ![]() , który oznacza wartość obecną takiej renty
, który oznacza wartość obecną takiej renty
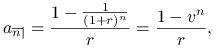 |
gdzie ![]() .
.
Ćwiczenie 9.2
Wyznacz wartość obecną
renty płatnej z góry przez ![]() lat. Wielkość pojedynczej wypłaty wynosi 1 jednostkę.
lat. Wielkość pojedynczej wypłaty wynosi 1 jednostkę.
Rozwiązanie
1 jednostka jest płatna na początku roku przez ![]() lat.
lat.
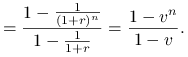 |
Alternatywnie, gdy zastąpimy ![]() przez
przez ![]() , to otrzymamy
, to otrzymamy
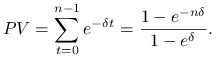 |
Odpowiedź.
Wartość obecna renty wynosi ![]() .
.
Komentarz.
Aktuariusze używają oznaczenia
Ćwiczenie 9.3
Udowodnij równość
Ćwiczenie 9.4
Wyznacz wartość obecną renty płatnej z dołu bezterminowo. Wielkość pojedynczej wypłaty wynosi 1 jednostkę.
Rozwiązanie
1 jest płatne na koniec każdego roku ” od dziś do końca świata”.
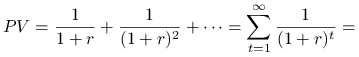 |
Odpowiedź.
Wartość obecna renty wynosi ![]() .
.
Komentarz.
Aktuariusze używają oznaczenia
Ćwiczenie 9.5
Wyznacz wartość obecną renty płatnej z góry bezterminowo. Wielkość pojedynczej wypłaty wynosi 1 jednostkę.
Rozwiązanie
1 jest płatne na początku każdego roku.
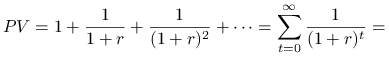 |
Odpowiedź.
Wartość obecna renty wynosi ![]() .
.
Komentarz.
Aktuariusze używają oznaczenia
Ćwiczenie 9.6
Wyznacz wartość obecną ciągłego stałego strumienia wypłat płatnego przez ![]() lat.
Wielkość rocznej wypłaty wynosi 1 jednostkę.
lat.
Wielkość rocznej wypłaty wynosi 1 jednostkę.
Rozwiązanie.
1 płatna w ciągu roku przez ![]() lat.
lat.
Mamy stałą gęstość płatności ![]() dla
dla ![]() .
.
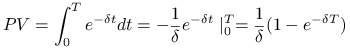 |
Odpowiedź.
Wartość obecna wynosi ![]() .
.
Komentarz.
Aktuariusze używają oznaczenia
Ćwiczenie 9.7
Wyznacz wartość obecną ciągłego stałego strumienia wypłat płatnego bezterminowo. Wielkość rocznej wypłaty wynosi 1 jednostkę.
Rozwiązanie.
1 płatna w ciągu roku bezterminowo.
Mamy stałą gęstość płatności ![]() dla
dla ![]() .
.
Odpowiedź.
Wartość obecna wynosi ![]() .
.
Komentarz.
Aktuariusze używają oznaczenia
Ćwiczenie 9.8
Wyznacz wartość obecną
renty odroczonej o ![]() lat płatnej z dołu przez
lat płatnej z dołu przez ![]() lat. Wielkość pojedynczej wypłaty wynosi 1 jednostkę.
lat. Wielkość pojedynczej wypłaty wynosi 1 jednostkę.
Rozwiązanie.
1 płatna ”z dołu” przez ![]() lat.
lat.
Odpowiedź.
Wartość obecna wynosi ![]() .
.
Ćwiczenie 9.9
Wyznacz wartość obecną
renty odroczonej o ![]() lat płatnej z dołu bezterminowo. Wielkość pojedynczej wypłaty wynosi 1 jednostkę.
lat płatnej z dołu bezterminowo. Wielkość pojedynczej wypłaty wynosi 1 jednostkę.
Rozwiązanie
1 płatna ”z dołu” bezterminowo.
Odpowiedź.
Wartość obecna wynosi ![]() .
.
Ćwiczenie 9.10
Wyznacz wartość obecną
renty płatnej z dołu ![]() razy w roku przez
razy w roku przez ![]() lat. Wielkość pojedynczej wypłaty wynosi
lat. Wielkość pojedynczej wypłaty wynosi ![]() jednostki.
jednostki.
Rozwiązanie.![]() płatne ”z dołu” przez
płatne ”z dołu” przez ![]() lat.
lat.
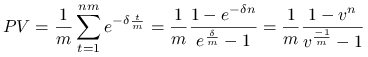 |
Odpowiedź.
Wartość obecna wynosi ![]() .
.
Komentarz.
Aktuariusze używają oznaczeń
Ćwiczenie 9.11
Wyznacz wartość obecną
renty płatnej z góry ![]() razy w roku przez
razy w roku przez ![]() lat. Wielkość pojedynczej wypłaty wynosi
lat. Wielkość pojedynczej wypłaty wynosi ![]() jednostki.
jednostki.
Rozwiązanie.![]() płatne ”z góry” przez
płatne ”z góry” przez ![]() lat.
lat.
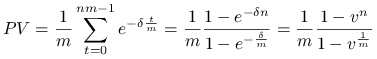 |
Odpowiedź.
Wartość obecna wynosi ![]() .
.
Komentarz.
Aktuariusze używają oznaczeń
Ćwiczenie 9.12
Wyznacz wartość obecną rewaloryzowanej liniowo
renty bezterminowej, płatnej z góry . Rewaloryzacja jest równa pierwszej wypłacie i wynosi ![]() jednostkę.
jednostkę.
Rozwiązanie.
Traktujemy tę rentę jak sumę odroczonych rent stałych.
Odpowiedź.
Wartość obecna wynosi ![]() .
.
Komentarz.
Aktuariusze używają oznaczenia
Ćwiczenie 9.13
Wyznacz wartość obecną rewloryzowanej liniowo raz na rok
renty bezterminowej, płatnej z góry ![]() razy w roku. Rewaloryzacja jest równa pierwszej wypłacie i wynosi
razy w roku. Rewaloryzacja jest równa pierwszej wypłacie i wynosi ![]() jednostki.
jednostki.
Rozwiązanie.
Odpowiedź.
Wartość obecna wynosi ![]() .
.
Komentarz.
Aktuariusze używają oznaczenia