Zagadnienia
12. Giełda. Rynek akcji – cd
12.1. Instrumenty pochodne
12.1.1. Wprowadzenie
Określenie.Instrument pochodny (derivative), to kontrakt finansowy, którego rozliczenie zależy od innego instrumentu
zwanego bazowym.
Typowe instrumenty bazowe:![]() akcje,
akcje,![]() indeksy i inne wskaźniki ekonomiczne,
indeksy i inne wskaźniki ekonomiczne,![]() obligacje,
obligacje,![]() stopy procentowe,
stopy procentowe,![]() kursy walut,
kursy walut,![]() ceny towarów,
ceny towarów,![]() inne instrumenty pochodne,
inne instrumenty pochodne,![]() instrumenty niefinansowe, zależne od pogody lub klęsk żywiołowych,
instrumenty niefinansowe, zależne od pogody lub klęsk żywiołowych,![]()
![]() .
.
We wrześniu 2010
na Giełdzie Papierów Wartościowych w Warszawie były notowane następujące instrumenty pochodne:![]() kontrakty terminowe – futures:
kontrakty terminowe – futures:
– na indeksy giełdowe: WIG20 i mWIG40,
– na akcje spółek giełdowych,
– na kursy walut USD i EUR;![]() opcje:
opcje:
– na indeks WIG20;![]() jednostki indeksowe (patrz 9.1.9):
jednostki indeksowe (patrz 9.1.9):
– na indeks WIG20;![]() produkty strukturyzowane (patrz 9.1.8).
produkty strukturyzowane (patrz 9.1.8).
12.1.2. Kontrakty terminowe – forward i futures
Określenie kontraktu terminowego forward.
Dwie strony, kupujący i sprzedający, umawiają się w momencie ![]() , że
w momencie
, że
w momencie ![]() w przyszłości dokonają transakcji kupna/sprzedaży określonej z góry
ilości towaru lub akcji, po ustalonej z góry cenie.
w przyszłości dokonają transakcji kupna/sprzedaży określonej z góry
ilości towaru lub akcji, po ustalonej z góry cenie.
W finansowych kontraktach terminowych rozliczenie na ogół ma formę pieniężną, tzn. następuje
przepływ gotówki, który zależy od różnicy między kursem terminowym
ustalonym w dniu ![]() , a aktualnym kursem instrumentu bazowego w dniu
, a aktualnym kursem instrumentu bazowego w dniu ![]() .
.
Przyjmijmy następujące oznaczenia:![]() – kurs terminowy w dniu
– kurs terminowy w dniu ![]() ,
,![]() – kurs instrumentu bazowego w dniu
– kurs instrumentu bazowego w dniu ![]() ,
,![]() – liczba jednostek instrumentu bazowego, na którą opiewa kontrakt.
– liczba jednostek instrumentu bazowego, na którą opiewa kontrakt.
Wówczas zysk (strata) kupującego wynosi:
a zysk (strata) sprzedającego:
Specyfika kontraktów futures związana jest ze sposobem zabezpieczania wykonania kontraktu, opartym na:
-
 rozliczeniach dziennych,
rozliczeniach dziennych,
-
 systemie depozytów,
systemie depozytów,
-
 udziale ,,trzeciego uczestnika” kontraktu – izby rozrachunkowej (clearing house).
W Polsce jest to
Krajowy Depozyt Papierów Wartościowych (KDPW).
udziale ,,trzeciego uczestnika” kontraktu – izby rozrachunkowej (clearing house).
W Polsce jest to
Krajowy Depozyt Papierów Wartościowych (KDPW).
Szczegółowe zasady rozliczeń ustala biuro maklerskie prowadzące rachunek inwestycyjny danego inwestora, w oparciu o wytyczne KDPW. Ogólny schemat jest następujący:
-
 W momencie zawarcia transakcji inwestor wnosi depozyt proporcjonalny do jej wielkości.
W momencie zawarcia transakcji inwestor wnosi depozyt proporcjonalny do jej wielkości. -
 Po każdej
sesji ustala się kurs rozliczeniowy (np. kurs zamknięcia). Na jego podstawie modyfikuje się depozyt.
Po każdej
sesji ustala się kurs rozliczeniowy (np. kurs zamknięcia). Na jego podstawie modyfikuje się depozyt. -
 Jeśli zmiany są niekorzystne dla inwestora, to musi on uzupełnić depozyt (w terminie do następnej sesji giełdowej).
Jeśli zmiany są niekorzystne dla inwestora, to musi on uzupełnić depozyt (w terminie do następnej sesji giełdowej). -
 Depozyt na ogół jest nieoprocentowany. Koszt utrzymania depozytu (stracone odsetki)
w istotny sposób wpływa na opłacalność inwestycji.
Depozyt na ogół jest nieoprocentowany. Koszt utrzymania depozytu (stracone odsetki)
w istotny sposób wpływa na opłacalność inwestycji.
Przeanalizujmy dokładniej mechanizm rozliczeń dziennych.
Niech ![]() oznacza kurs rozliczeniowy w dniu
oznacza kurs rozliczeniowy w dniu ![]() .
Dzienny zysk (strata) nabywcy pojedynczego kontraktu wynosi
.
Dzienny zysk (strata) nabywcy pojedynczego kontraktu wynosi
a dzienny zysk (strata) sprzedawcy
Kwoty te zostaną odpowiednio pobrane lub doliczone do depozytu.
Stosowane są dwa sposoby uzupełniania depozytu.
I. Ustala się jedną poprzeczkę ![]() . Obowiązkowy depozyt w dniu
. Obowiązkowy depozyt w dniu ![]() wynosi
wynosi ![]() .
Gdy zmienia się kurs rozliczenia, następuje przepływ gotówki między kontem inwestora a depozytem.
W przypadku nabywcy pojedynczego kontraktu kwota ta wynosi
.
Gdy zmienia się kurs rozliczenia, następuje przepływ gotówki między kontem inwestora a depozytem.
W przypadku nabywcy pojedynczego kontraktu kwota ta wynosi
Gdy ![]() , to musi on uzupełnić depozyt, a gdy
, to musi on uzupełnić depozyt, a gdy ![]() , to pieniądze wpłyną
na jego konto. W przypadku sprzedawcy
, to pieniądze wpłyną
na jego konto. W przypadku sprzedawcy
Gdy ![]() , to musi on uzupełnić depozyt, a gdy
, to musi on uzupełnić depozyt, a gdy ![]() , to pieniądze wpłyną
na jego konto.
, to pieniądze wpłyną
na jego konto.
II. Ustala się dwie poprzeczki ![]() .
W przypadku, gdy
.
W przypadku, gdy ![]() , inwestor musi uzupełnić depozyt do poziomu
, inwestor musi uzupełnić depozyt do poziomu
![]() . Przy znacznym przekroczeniu poziomu
. Przy znacznym przekroczeniu poziomu ![]() inwestor może pobrać nadwyżkę z depozytu.
inwestor może pobrać nadwyżkę z depozytu.
Kontrakt futures można zamknąć na dwa sposoby:![]() W momencie wygaśnięcia kontraktu, przez rozliczenie.
W momencie wygaśnięcia kontraktu, przez rozliczenie.![]() W dowolnym momencie, przez zawarcie kontraktu przeciwnego.
W dowolnym momencie, przez zawarcie kontraktu przeciwnego.
Na warszawskiej GPW kontrakty futures mają sześcioznakowe oznaczenia np.: kontrakt futures na indeks WIG20 rozliczany w grudniu 2002 miał symbol: FW20Z2.
Poszczególne fragmenty kodu oznaczają:
F – typ kontraktu (futures),
W20 – instrument bazowy (WIG20),
Z – miesiąc wykonania (grudzień),
2 – rok wykonania (2002).
Oznaczenia miesięcy wykonania kontraktów terminowych są następujące:
| miesiąc | kod | miesiąc | kod |
| styczeń | F | lipiec | N |
| luty | G | sierpień | Q |
| marzec | H | wrzesień | U |
| kwiecień | J | październik | V |
| maj | K | listopad | X |
| czerwiec | M | grudzień | Z |
12.1.3. Wycena kontraktów forward i futures
12.1.3.1. Ogólne zasady wyceny kontraktów terminowych
Wycena kontraktów terminowych opiera się na dwóch regułach:
zasadzie braku arbitrażu i prawie jednej ceny ([33] §1.2).
Niech ![]() oznacza zainwestowane środki, a
oznacza zainwestowane środki, a ![]() przyszłą wypłatę (modelowaną jako zmienna losowa).
przyszłą wypłatę (modelowaną jako zmienna losowa).
Definicja 12.1
Mówimy, że na rynku zachodzi arbitraż, gdy jest możliwa inwestycja taka, że
Czyli nie inwestując własnych środków, nie ryzykując straty, można z niezerowym prawdopodobieństwem coś zyskać.
Wniosek 12.1
Na rynku nie ma arbitrażu, gdy zachodzą następujące równoważne warunki:
Inwestycja, która na pewno nie przyniesie strat, a może przynieść zysk, wymaga zainwestowania niezerowych środków.
Inwestycja, która nie wymaga żadnych nakładów i na pewno nie przyniesie strat, nie przyniesie również zysku.
Definicja 12.2
Mówimy, że na rynku obowiązuje prawo jednej ceny, gdy każde dwie inwestycje o tych samych przyszłych przepływach gotówki mają tę samą cenę.
12.1.3.2. Model rynku doskonałego
Kurs teoretyczny instrumentów pochodnych najczęściej wyznacza się w oparciu o tzw. model rynku doskonałego ([19] §1.7). Zakładamy mianowicie, że:
-
Stopy procentowe lokat i kredytów bankowych są jednakowe (pomijamy marże).
-
Wysokość zaciąganych przez inwestorów kredytów bankowych nie jest w żaden sposób ograniczona.
-
Wszystkie aktywa są doskonale podzielne. Można kupować i sprzedawać dowolne ilości wszystkich instrumentów (zarówno bardzo małe, jak i bardzo duże). Zapewniona jest więc idealna płynność obrotu.
-
Dopuszczalna jest nieograniczona krótka sprzedaż wszystkich instrumentów (w szczególności akcji). Wszystkie transakcje są odwracalne. Jeżeli dopuszczalna jest transakcja, która generuje przepływy gotówki równe
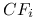 w chwilach
w chwilach 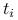 , to dopuszczalna jest też transakcja generująca przepływy gotówki
, to dopuszczalna jest też transakcja generująca przepływy gotówki
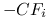 w tych samych momentach czasu
w tych samych momentach czasu 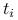 .
. -
Inwestorzy nie ponoszą żadnych dodatkowych kosztów związanych z zawieraniem transakcji i nie są wymagane depozyty zabezpieczające.
-
Zyski z inwestowania w dowolne instrumenty finansowe nie są obciążone podatkami.
Koszty transakcyjne, depozyty i inne ograniczenia odgrywają w modelach rynku finansowego podobną rolę jak tarcie w statyce. Dlatego też rynek doskonały nazywa się rynkiem pozbawionym tarcia (frictionless market).
Lemat 12.1
Na rynku doskonałym z zasady braku arbitrażu wynika prawo jednej ceny.
Dowód.
Załóżmy, że na naszym rynku nie obowiązuje prawo jednej ceny. Wówczas
dopuszczalne są dwie transakcje A i B, które (prawie na pewno) generują tę samą wypłatę
w tym samym momencie czasu ![]() , ale w transakcję A trzeba zainwestować więcej niż w B
, ale w transakcję A trzeba zainwestować więcej niż w B
Z założenia 4 modelu rynku doskonałego wynika, że dopuszczalna jest transakcja C:
Inwestor zawiera transakcję B, transakcję odwrotną do A (krótko sprzedaje A) oraz lokuje w banku kwotę
![]() .
Wówczas
.
Wówczas
czyli nakłady potrzebne do zawarcia C są zerowe.
W momencie ![]() inwestor rozlicza transakcję B, transakcję odwrotną do A i wyjmuje pieniądze z banku wraz
z odsetkami (okresowa stopa procentowa
inwestor rozlicza transakcję B, transakcję odwrotną do A i wyjmuje pieniądze z banku wraz
z odsetkami (okresowa stopa procentowa ![]() ). Zatem, prawie na pewno
). Zatem, prawie na pewno
Co jest sprzeczne z zasadą braku arbitrażu. Zatem na
rynku doskonałym
zasada braku arbitrażu pociąga za sobą prawo jednej ceny.
Uwaga. Aczkolwiek na rynku doskonałym
z zasady braku arbitrażu wynika prawo jednej ceny, to w bardziej realistycznych modelach prawo jednej ceny
może nie obowiązywać.
12.1.3.3. Wycena kontraktów forward – rynek doskonały
Na początek zajmiemy się wyceną kontraktów forward
na rynku doskonałym.
Ograniczamy się do dwóch
przepływów gotówki: w momencie zawarcia transakcji i w momencie jej rozliczenia. Ponadto zakładamy,
że wszystkie rozpatrywane transakcje mają ten sam czas życia ![]() .
.
Będziemy rozpatrywali następujące transakcje ,,elementarne”:
-
 zakup obligacji o stałym oprocentowaniu;
zakup obligacji o stałym oprocentowaniu; 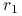 stopa zwrotu po czasie
stopa zwrotu po czasie 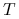 ;
; -
 zakup akcji spółki ABC;
zakup akcji spółki ABC; 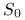 cena w momencie początkowym,
cena w momencie początkowym, 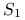 cena po czasie
cena po czasie 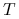 ;
; -
 kupno lub sprzedaż kontraktu terminowego na akcje spółki ABC o czasie życia
kupno lub sprzedaż kontraktu terminowego na akcje spółki ABC o czasie życia 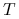 ;
;
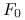 cena terminowa w momencie początkowym,
cena terminowa w momencie początkowym, 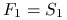 cena w momencie rozliczenia.
cena w momencie rozliczenia.
W momencie zawarcia transakcji wszystkie wielkości z wyjątkiem ![]() są znane.
są znane.
Lemat 12.2
Z prawa jednej ceny wynika, że
Dowód.
Będziemy analizować
następujące dwie transakcje:
A1. Sprzedaż 1 kontraktu terminowego i kupno 1 akcji.
A2. Zakup obligacji za kwotę ![]()
Rozliczenie.
Przepływy gotówki w momencie zawarcia transakcji A1 i A2
Przepływy gotówki w momencie rozliczenia A1 i A2
Rozliczenie kontraktu terminowego, sprzedaż akcji.
Wykup obligacji plus odsetki.
Zauważmy, że oba przepływy ![]() i
i ![]() są równe.
Z prawa jednej ceny wynika, że
są równe.
Z prawa jednej ceny wynika, że
![]() Czyli
Czyli
Co kończy dowód.
W dalszym ciągu ceny wyznaczone w oparciu o model rynku doskonałego będziemy nazywać cenami
teoretycznymi. Uproszczenia modelowe powodują, że mogą się one trochę różnić od cen rynkowych
wyznaczonych przez aktualny popyt
i aktualną podaż na rzeczywistym rynku.
12.1.3.4. Wycena kontraktów forward – rynek z tarciem
Dla uproszczenia pomijamy koszty transakcyjne. Tak jak poprzednio ograniczamy się do dwóch
przepływów gotówki: w momencie zawarcia transakcji i w momencie jej rozliczenia. Ponadto zakładamy,
że wszystkie rozpatrywane transakcje mają ten sam czas życia ![]() .
.
Będziemy rozpatrywali transakcje złożone z następujących transakcji elementarnych:
-
 zakup obligacji;
zakup obligacji; 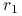 – stopa zwrotu po czasie
– stopa zwrotu po czasie 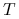 ;
; -
 pożyczka w banku;
pożyczka w banku; 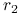 – oprocentowanie po czasie
– oprocentowanie po czasie 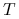 ;
; -
 zakup akcji spółki ABC;
zakup akcji spółki ABC; 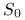 – cena w momencie początkowym,
– cena w momencie początkowym, 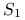 – cena po czasie
– cena po czasie 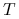 ;
; -
 krótka sprzedaż akcji spółki ABC;
krótka sprzedaż akcji spółki ABC; 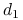 – depozyt,
– depozyt,
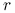 – oprocentowanie depozytu po czasie
– oprocentowanie depozytu po czasie 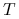 ;
; -
 kupno lub sprzedaż kontraktu terminowego na akcje spółki ABC o czasie życia
kupno lub sprzedaż kontraktu terminowego na akcje spółki ABC o czasie życia 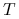 ;
;
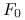 – cena terminowa w momencie początkowym,
– cena terminowa w momencie początkowym, 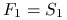 – cena w momencie rozliczenia,
– cena w momencie rozliczenia,
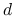 – depozyt,
– depozyt, 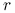 – oprocentowanie depozytu po czasie
– oprocentowanie depozytu po czasie 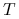 .
.
W momencie zawarcia transakcji wszystkie wielkości z wyjątkiem ![]() są znane. Będziemy analizować
następujące dwie pary i dwie pojedyncze transakcje:
są znane. Będziemy analizować
następujące dwie pary i dwie pojedyncze transakcje:
A1. Sprzedaż 1 kontraktu terminowego i kupno 1 akcji.
A2. Zakup obligacji za kwotę ![]()
B1. Kupno 1 kontraktu terminowego i zakup obligacji za kwotę ![]()
B2. Kupno 1 akcji.
C. Sprzedaż 1 kontraktu terminowego, kupno 1 akcji i pożyczka z banku kwoty ![]()
D. Kupno 1 kontraktu terminowego, krótka sprzedaż 1 akcji i zakup obligacji za kwotę ![]()
(gdyby ![]() okazało się ujemne, należy zastąpić zakup obligacji kredytem).
okazało się ujemne, należy zastąpić zakup obligacji kredytem).
Pary A i B posłużą jako przykład ewentualnego zastosowania prawa jednej ceny. Natomiast inwestycje
C i D – zasady braku arbitrażu.
Rozliczenie A.
Przepływy gotówki w momencie zawarcia transakcji A1 i A2
Przepływy gotówki w momencie rozliczenia A1 i A2
Zwrot depozytu wraz z oprocentowaniem, rozliczenie kontraktu terminowego, sprzedaż akcji.
Wykup obligacji plus odsetki.
Zauważmy, że oba przepływy ![]() i
i ![]() są równe.
Gdyby obowiązywało prawo jednej ceny, to mielibyśmy
są równe.
Gdyby obowiązywało prawo jednej ceny, to mielibyśmy
![]() Czyli
Czyli
Oznaczmy przez ![]() cenę kontraktu terminowego, spełniającą powyższą równość. Mamy
cenę kontraktu terminowego, spełniającą powyższą równość. Mamy
Podsumowując, gdy ![]() , to rynek jest w równowadze (obowiązuje prawo jednej ceny).
W pozostałych przypadkach rynek nie jest w równowadze.
Gdy
, to rynek jest w równowadze (obowiązuje prawo jednej ceny).
W pozostałych przypadkach rynek nie jest w równowadze.
Gdy ![]() , to bardziej opłacalna jest inwestycja A1. Oznacza to zwiększoną liczbę ofert
sprzedaży kontraktu terminowego, a zatem spadek ceny terminowej
, to bardziej opłacalna jest inwestycja A1. Oznacza to zwiększoną liczbę ofert
sprzedaży kontraktu terminowego, a zatem spadek ceny terminowej ![]() .
.
Rozliczenie B.
Przepływy gotówki w momencie zawarcia transakcji B1 i B2
Przepływy gotówki w momencie rozliczenia B1 i B2
Zwrot depozytu wraz z oprocentowaniem, rozliczenie kontraktu terminowego, wykup obligacji plus odsetki.
Sprzedaż akcji.
Zauważmy, że oba przepływy ![]() i
i ![]() są równe.
Gdyby obowiązywało prawo jednej ceny, to mielibyśmy
są równe.
Gdyby obowiązywało prawo jednej ceny, to mielibyśmy
![]() Czyli
Czyli
Oznaczmy przez ![]() cenę kontraktu terminowego spełniającą powyższą równość. Mamy
cenę kontraktu terminowego spełniającą powyższą równość. Mamy
Podsumowując, gdy ![]() , to rynek jest w równowadze (obowiązuje prawo jednej ceny).
W pozostałych przypadkach rynek nie jest w równowadze.
Gdy
, to rynek jest w równowadze (obowiązuje prawo jednej ceny).
W pozostałych przypadkach rynek nie jest w równowadze.
Gdy ![]() , to bardziej opłacalna jest inwestycja B1. Oznacza to zwiększoną liczbę ofert
kupna kontraktu terminowego, a zatem wzrost ceny terminowej
, to bardziej opłacalna jest inwestycja B1. Oznacza to zwiększoną liczbę ofert
kupna kontraktu terminowego, a zatem wzrost ceny terminowej ![]() .
.
Biorąc pod uwagę, że oprocentowanie depozytu nie może przewyższać oprocentowania obligacji, otrzymujemy nierówność
Gdy powyższa nierówność jest ostra, to prawo jednej ceny nie obowiązuje. Mamy całe pasmo cen
quasi-równowagi.
Równość zachodzi tylko, gdy ![]() (nie ma depozytu) lub
(nie ma depozytu) lub ![]() (depozyt jest oprocentowany na poziomie oprocentowania obligacji).
Wówczas prawo jednej ceny wyznacza teoretyczną cenę terminową
(depozyt jest oprocentowany na poziomie oprocentowania obligacji).
Wówczas prawo jednej ceny wyznacza teoretyczną cenę terminową
Rozliczenie C.
Przepływ gotówki w momencie zawarcia transakcji C
Przepływ gotówki w momencie rozliczenia
Zwrot depozytu wraz z oprocentowaniem, rozliczenie kontraktu terminowego, sprzedaż akcji
i spłata kredytu wraz z odsetkami.
Oznaczmy przez ![]() cenę kontraktu terminowego, dla której zachodzi równość
cenę kontraktu terminowego, dla której zachodzi równość ![]() .
.
Zauważmy, że gdy ![]() , to
, to ![]() i nasza transakcja jest transakcją arbitrażową.
Wzmożone zainteresowanie transakcją C
oznacza zwiększony popyt na kontrakty sprzedaży, a więc spadek ceny terminowej
i nasza transakcja jest transakcją arbitrażową.
Wzmożone zainteresowanie transakcją C
oznacza zwiększony popyt na kontrakty sprzedaży, a więc spadek ceny terminowej ![]() .
.
Gdy ![]() , to
, to ![]() i nasza transakcja nie jest transakcją arbitrażową.
i nasza transakcja nie jest transakcją arbitrażową.
Rozliczenie D.
Przepływ gotówki w momencie zawarcia transakcji D
depozyt kontraktu terminowego, krótka sprzedaż, depozyt zabezpieczający krótką sprzedaż i zakup obligacji.
Przepływ gotówki w momencie rozliczenia
Zwrot depozytu wraz z oprocentowaniem, rozliczenie kontraktu terminowego, sprzedaż akcji
i spłata kredytu wraz z odsetkami.
Oznaczmy przez ![]() cenę kontraktu terminowego, dla której zachodzi równość
cenę kontraktu terminowego, dla której zachodzi równość ![]() .
.
Zauważmy, że gdy ![]() , to
, to ![]() i nasza transakcja jest transakcją arbitrażową. Wzmożone zainteresowanie transakcją D
oznacza zwiększony popyt na kontrakty kupna, a więc wzrost ceny terminowej
i nasza transakcja jest transakcją arbitrażową. Wzmożone zainteresowanie transakcją D
oznacza zwiększony popyt na kontrakty kupna, a więc wzrost ceny terminowej ![]() .
.
Gdy ![]() , to
, to ![]() i nasza transakcja nie jest transakcją arbitrażową.
i nasza transakcja nie jest transakcją arbitrażową.
Zauważmy, że gdy ![]() , to zachodzą następujące nierówności
, to zachodzą następujące nierówności
Jak widać, pasmo cenowe wyznaczone przez zasadę braku arbitrażu jest szersze niż pasmo cen quasi-równowagi.
Natomiast, gdy
oprocentowanie obligacji jest takie samo jak oprocentowanie kredytu, ![]() ,
oraz nie ma depozytu
,
oraz nie ma depozytu ![]() , lub jest on oprocentowany na poziomie oprocentowania obligacji
, lub jest on oprocentowany na poziomie oprocentowania obligacji ![]() ,
to
,
to
W takim przypadku zasada braku arbitrażu wyznacza tę samą cenę teoretyczną, co prawo jednej ceny.
12.1.3.5. Wycena kontraktów futures
Wycena przedstawiona poniżej jest wyceną uproszczoną
([19] §1.7),
dokonaną z pominięciem
kosztów transakcyjnych, depozytów i marż.
Ponadto zakładamy, że inwestor może ,,wkładać” i ,,pożyczać” pieniądze z rachunku bankowego, który będzie
modelowany za pomocą deterministycznego procesu akumulacji
![]() ,
, ![]() .
1 włożona na rachunek bankowy w chwili
.
1 włożona na rachunek bankowy w chwili ![]() akumuluje do
akumuluje do ![]() w chwili
w chwili ![]() .
Podobnie, aby spłacić 1 pożyczoną w chwili
.
Podobnie, aby spłacić 1 pożyczoną w chwili ![]() , trzeba w chwili
, trzeba w chwili ![]() wpłacić
wpłacić ![]() .
.
![]() i
i ![]() oznaczają odpowiednio cenę instrumentu bazowego i kurs terminowy w chwili
oznaczają odpowiednio cenę instrumentu bazowego i kurs terminowy w chwili ![]() .
W dalszym ciągu będziemy zakładać, że oba instrumenty są nieskończenie podzielne.
.
W dalszym ciągu będziemy zakładać, że oba instrumenty są nieskończenie podzielne.
Lemat 12.3
Z prawa jednej ceny wynika, że kurs terminowy w chwili ![]() wynosi
wynosi
gdzie ![]() – moment zapadalności kontraktu futures.
– moment zapadalności kontraktu futures.
Dowód.
Niech ![]() – moment rozpoczęcia inwestycji,
– moment rozpoczęcia inwestycji, ![]() – moment zapadalności kontraktu futures,
a
– moment zapadalności kontraktu futures,
a ![]() – momenty rozliczeń dziennych kontraktu.
– momenty rozliczeń dziennych kontraktu.
Aby dokonać wyceny, porównamy dwie strategie.
A. Kupujemy 1 jednostkę instrumentu bazowego (np. 1 akcję) w chwili ![]() i sprzedajemy ją w chwili
i sprzedajemy ją w chwili ![]() .
.
B. Wkładamy na rachunek bankowy kwotę
w kolejnych momentach ![]() ,
, ![]() kupujemy kontrakty terminowe, tak aby po zakupie
w chwili
kupujemy kontrakty terminowe, tak aby po zakupie
w chwili ![]() posiadać ich następującą ilość:
posiadać ich następującą ilość:
Straty z rozliczeń dziennych pokrywamy z rachunku bankowego, a zyski wpłacamy na ten rachunek.
W momencie ![]() wyjmujemy pieniądze z rachunku bankowego i rozliczamy kontrakt futures.
wyjmujemy pieniądze z rachunku bankowego i rozliczamy kontrakt futures.
Rozliczenie strategii A.
Przepływ gotówki w momencie ![]()
Przepływ gotówki w momencie ![]()
Rozliczenie strategii B.
Przepływ gotówki w momencie ![]()
Przepływ gotówki w momencie ![]()
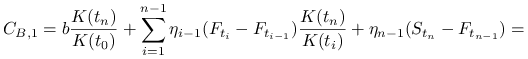 |
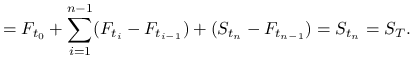 |
Ponieważ w momencie zapadalności ![]() przepływy gotówki obu inwestycji są identyczne, to
z prawa jednej ceny wynika, że w momencie
przepływy gotówki obu inwestycji są identyczne, to
z prawa jednej ceny wynika, że w momencie ![]() też są równe
też są równe
Zatem
Czyli
Uwaga.
Warto zauważyć, że jeżeli przyjmiemy, że stopa zwrotu ![]() z obligacji o terminie zapadalności
z obligacji o terminie zapadalności ![]() zakupionej w chwili
zakupionej w chwili ![]() jest wyznaczona przez deterministyczny proces akumulacji
jest wyznaczona przez deterministyczny proces akumulacji ![]()
to otrzymane przez nas teoretyczne ceny terminowe kontraktów forward i futures na ten sam instrument bazowy
są sobie równe.
12.1.4. Opcje
Najbardziej popularne są opcje europejskie
i amerykańskie.
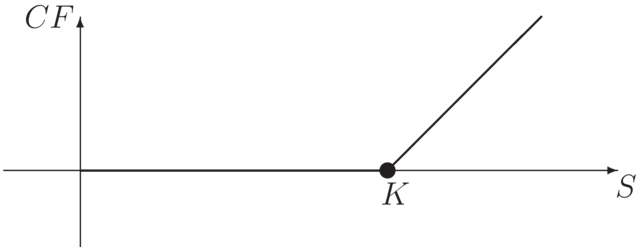
Europejska opcja kupna (call), to kontrakt gwarantujący
w ustalonym momencie ![]() w przyszłości,
prawo zakupu akcji (lub innego instrumentu bazowego)
po ustalonej z góry cenie
w przyszłości,
prawo zakupu akcji (lub innego instrumentu bazowego)
po ustalonej z góry cenie ![]() .
.
Posiadacz opcji nie ma obowiązku jej realizacji. Zatem realizuje ją tylko,
gdy cena ![]() instrumentu bazowego w dniu
instrumentu bazowego w dniu ![]() jest wyższa od ceny wykonania
jest wyższa od ceny wykonania ![]() .
Wypłata posiadacza opcji call w dniu rozliczenia
.
Wypłata posiadacza opcji call w dniu rozliczenia ![]() wynosi
wynosi
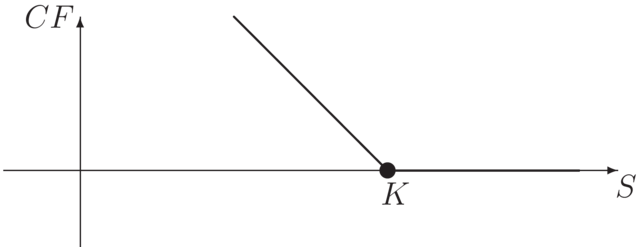
Europejska opcja sprzedaży (put), to kontrakt gwarantujący
w ustalonym momencie ![]() w przyszłości,
prawo sprzedaży akcji (lub innego instrumentu bazowego)
po ustalonej z góry cenie
w przyszłości,
prawo sprzedaży akcji (lub innego instrumentu bazowego)
po ustalonej z góry cenie ![]() .
.
Posiadacz opcji nie ma obowiązku jej realizacji. Zatem realizuje ją tylko,
gdy cena ![]() instrumentu bazowego w dniu
instrumentu bazowego w dniu ![]() jest niższa od ceny wykonania
jest niższa od ceny wykonania ![]() .
Wypłata posiadacza opcji put w dniu rozliczenia
.
Wypłata posiadacza opcji put w dniu rozliczenia ![]() wynosi
wynosi
Opcje amerykańskie różnią się od europejskich tym, że ich posiadacz może je zrealizować
w dowolnym wybranym przez siebie momencie, aż do ich wygaśnięcia.
Od 22 września 2003 na Giełdzie Warszawskiej są w obrocie opcje
na indeks WIG20.
Przykład:
OW20C4140
O – opcja europejska,
W20 – na indeks WIG20,
C4 – kupna, zapadalna w marcu 2004,
140 – o kursie wykonania 1400 pkt.
Czwarty znak kodu określa typ call albo put i miesiąc wykonania.
| miesiąc | opcja lub warrant | opcja lub warrant |
| kupna (call) | sprzedaży (put) | |
| styczeń | A | M |
| luty | B | N |
| marzec | C | O |
| kwiecień | D | P |
| maj | E | Q |
| czerwiec | F | R |
| lipiec | G | S |
| sierpień | H | T |
| wrzesień | I | U |
| październik | J | V |
| listopad | K | W |
| grudzień | L | X |
12.1.5. Wycena opcji europejskich
Założenia:
1. Nie ma kosztów transakcyjnych, marż, depozytów itp.
2. Dopuszczalna jest krótka sprzedaż instrumentu bazowego (akcji).
Oznaczenia: ![]() – struktura terminowa
czynnika dyskontującego w dniu
– struktura terminowa
czynnika dyskontującego w dniu ![]() ,
,
![]() – dzień rozliczenia,
– dzień rozliczenia,
![]() – cena wykonania,
– cena wykonania,
![]() – cena instrumentu bazowego w dniu
– cena instrumentu bazowego w dniu ![]() ,
,
![]() i
i ![]() – ceny opcji kupna (call) i sprzedaży (put) w dniu
– ceny opcji kupna (call) i sprzedaży (put) w dniu ![]() ,
, ![]() .
.
Uwaga: Cenę opcji nazywa się też
premią.
12.1.5.1. Ograniczenia na ceny opcji
Lemat 12.4
Z zasady braku arbitrażu wynikają następujące oszacowania
Dowód.
Krok 1.
Wypłata z opcji jest nieujemna, zatem ![]() i
i ![]() .
.
Krok 2.
Rozważmy następującą inwestycję:
Zakup 1 opcji call, ![]() obligacji o terminie zapadalności
obligacji o terminie zapadalności ![]() i wypłacie 1 oraz krótka sprzedaż 1
instrumentu bazowego.
i wypłacie 1 oraz krótka sprzedaż 1
instrumentu bazowego.
Rozliczenie:
Ponieważ wypłata jest nieujemna, to ![]() , czyli
, czyli
Co razem z udowodnioną powyżej nieujemnością ceny ![]() daje prawą stronę pierwszego oszacowania.
daje prawą stronę pierwszego oszacowania.
Krok 3.
Rozważmy następującą inwestycję:
Zakup 1 opcji put, zakup 1 instrumentu bazowego oraz pożyczkę kwoty ![]() .
.
Rozliczenie:
Ponieważ wypłata jest nieujemna, to ![]() , czyli
, czyli
Co razem z udowodnioną powyżej nieujemnością ceny ![]() daje prawą stronę drugiego oszacowania.
daje prawą stronę drugiego oszacowania.
Krok 4.
Zauważmy, że wypłata z opcji put nie przekracza kwoty ![]() , a z opcji call jest mniejsza niż
, a z opcji call jest mniejsza niż ![]() . Zatem
. Zatem
Co daje lewe strony obu oszacowań.
Lemat 12.5
Parytet kupna-sprzedaży.
Z prawa jednej ceny wynika następujący parytet
Dowód.
Rozważmy następujące dwie inwestycje:
A. Zakup 1 opcji call i ![]() obligacji o terminie zapadalności
obligacji o terminie zapadalności ![]() i wypłacie 1,
i wypłacie 1,
B. Zakup 1 opcji put i zakup 1 instrumentu bazowego.
Rozliczenie A:
Rozliczenie B:
Zauważmy, że
Zatem obie inwestycje generują te same wypłaty. Czyli wymagają takich samych nakładów
Co kończy dowód.
Jeżeli założymy dodatkowo, że struktura terminowa jest płaska
gdzie ![]() – stała intensywność oprocentowania, to oszacowania z lematu przyjmują postać:
– stała intensywność oprocentowania, to oszacowania z lematu przyjmują postać:
a parytet kupna-sprzedaży możemy zapisać w następujący sposób:
(patrz [48] §4.5.3, §4.5.5).
12.1.5.2. Wzór Blacka-Scholesa
Założenia dodatkowe:
-
3. Struktura terminowa jest zadana przez deterministyczny proces akumulacji postaci
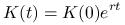
modelowany przez rachunek bankowy. W szczególności struktura terminowa jest płaska i nie zmienia się z upływem czasu.
-
4. Proces cen instrumentu bazowego jest opisany geometrycznym ruchem
Browna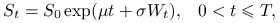
gdzie
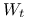 proces Wienera ([21] §13.1). W szczególności dla ustalonego
proces Wienera ([21] §13.1). W szczególności dla ustalonego 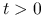
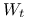 ma rozkład normalny,
ma rozkład normalny,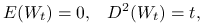
a dryf
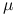 i volatility
i volatility 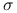 są stałe.
są stałe.
Z zasady braku arbitrażu wyprowadza się następujący wzór na cenę opcji kupna zwany wzorem Blacka-Scholesa [19] s. 50, [48] s. 188)
gdzie ![]() dystrybuanta standardowego rozkładu normalnego N(0,1), oraz
dystrybuanta standardowego rozkładu normalnego N(0,1), oraz
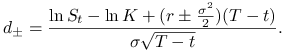 |
Wzór na cenę opcji put otrzymujemy z parytetu kupna-sprzedaży.
Zauważmy, że w powyższych wzorach tylko pierwsze cztery argumenty są znane.
Volatility ![]() należy wyznaczyć na podstawie badania rynku.
należy wyznaczyć na podstawie badania rynku.
Szkic wyprowadzenia wzoru.
Dowodzi się, że z zasady braku arbitrażu wynika istnienie pewnej miary probabilistycznej ![]() takiej, że cena opcji jest równa zdyskontowanej wartości oczekiwanej wypłaty obliczonej w tej mierze
takiej, że cena opcji jest równa zdyskontowanej wartości oczekiwanej wypłaty obliczonej w tej mierze
oraz ![]() gdzie
gdzie ![]() ma rozkład normalny (w mierze
ma rozkład normalny (w mierze ![]() )
)
Zatem zadanie sprowadza się do obliczenia całki
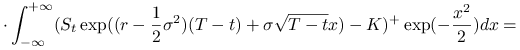 |
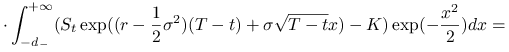 |
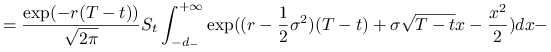 |
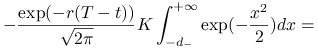 |
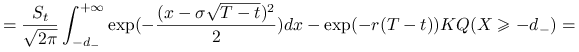 |
12.2. Ćwiczenia
Ćwiczenie 12.1
Bank Inwestycyjny handluje opcjami europejskimi na akcje spółki ,,ABCD”.
W swoim portfelu ma 100 opcji call z ceną wykonania 10 USD
i 200 opcji put z ceną wykonania 20 USD. Ponadto bank wystawił 100 opcji call z ceną wykonania 50 USD.
Przyjmując, że wszystkie opcje mają ten sam termin wykonania, oblicz,
dla jakich kursów akcji spółki ,,ABCD” (w dniu wykonania) wypłata będzie najmniejsza, a dla jakich największa.
Rozwiązanie. Wypłata z opcji call z ceną wykonania 10 wynosi
z opcji put z ceną wykonania 20
a z opcji call z ceną wykonania 50
Wypłata z całego portfela wynosi
![W(S)=100C_{{10}}+200P_{{20}}-100C_{{50}}=\left\{\begin{array}[]{ccc}200(20-S)&\mbox{ dla }&S\in\langle 0,10),\\
100(30-S)&\mbox{ dla }&S\in\langle 10,20),\\
100(S-10)&\mbox{ dla }&S\in\langle 20,50),\\
4000&\mbox{ dla }&S\in\langle 50,+\infty).\\
\end{array}\right.](wyklady/rka/mi/mi1299.png) |
Zauważmy, że ![]() , w przedziale
, w przedziale ![]()
![]() maleje,
maleje,
![]() , w przedziale
, w przedziale ![]() rośnie, a następnie stabilizuje się na poziomie 4000.
rośnie, a następnie stabilizuje się na poziomie 4000.
Odpowiedź.
Najmniejsza wypłata (równa 1000 USD) będzie miała miejsce gdy kurs akcji spółki ,,ABCD” wyniesie 20 USD,
a największa (równa 4000 USD), gdy kurs będzie większy lub równy 50 USD lub gdy spółka zbankrutuje.
Ćwiczenie 12.2
Inwestor zakupił i sprzedał pewną liczbę opcji put i opcji call o tym samym terminie zapadalności.
Wykres wypłaty z jego portfela opcyjnego, w zależności od aktywu bazowego, jest łamaną o wierzchołkach w punktach
(0,5), (5,0), (7,4), (9,0). Wiedząc, że ,,na prawo” od punktu (9,0) wykres jest półprostą nachyloną do osi ![]() pod kątem
pod kątem ![]() wyznacz przykładowy skład portfela.
wyznacz przykładowy skład portfela.
Rozwiązanie.
Oznaczmy przez ![]() funkcję wypłaty a przez
funkcję wypłaty a przez ![]() łamaną bedącą jej wykresem.
Skład portfela nie jest wyznaczony jednoznacznie przez treść zadania.
Dowolność tkwi w wyborze ”części put” portfela.
Jeśli w skład portfela mają wchodzić opcje put o cenie wykonania
łamaną bedącą jej wykresem.
Skład portfela nie jest wyznaczony jednoznacznie przez treść zadania.
Dowolność tkwi w wyborze ”części put” portfela.
Jeśli w skład portfela mają wchodzić opcje put o cenie wykonania ![]() ,
, ![]() , to ich liczby
, to ich liczby ![]() muszą
spełniać dwa równania liniowe:
muszą
spełniać dwa równania liniowe:
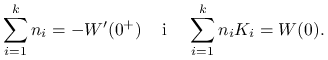 |
Cena wykonania opcji call wchodzącej w skład portfela jest albo współrzędną ![]() wierzchołka łamanej
wierzchołka łamanej ![]() albo jest równa cenie wykonania pewnej opcji put wchodzącej w skład portfela.
albo jest równa cenie wykonania pewnej opcji put wchodzącej w skład portfela.
Ponieważ kąt nachylenia pierwszego odcinka ![]() do osi
do osi ![]() wynosi
wynosi ![]() , to pochodna prawostronna
, to pochodna prawostronna ![]() w punkcie 0
w punkcie 0 ![]() wynosi -1 i możemy przyjąć
wynosi -1 i możemy przyjąć ![]() ,
, ![]() i
i ![]() .
Wówczas część call naszego portfela będzie się składać z
.
Wówczas część call naszego portfela będzie się składać z ![]() opcji o cenie wykonania 5,
opcji o cenie wykonania 5,
![]() o cenie wykonania 7 i
o cenie wykonania 7 i ![]() o cenie wykonania 9.
Wielkość
o cenie wykonania 9.
Wielkość ![]() wyznaczamy z warunku
wyznaczamy z warunku ![]() ,
,
Otrzymujemy ![]() .
Podobnie
.
Podobnie ![]() wyznaczamy z warunku
wyznaczamy z warunku ![]() ,
,
Otrzymujemy ![]() .
.
,,Na prawo” od punktu (9,0) ![]() jest półprostą nachyloną do osi
jest półprostą nachyloną do osi ![]() pod kątem
pod kątem ![]() , zatem
, zatem ![]() .
W ten sposób otrzymujemy warunek na sumę
.
W ten sposób otrzymujemy warunek na sumę ![]() .
.
Co daje ![]() .
.
Odpowiedź. Aby uzyskać zadaną funkcję wypłaty inwestor mógł na przykład zakupić 1 opcję put z ceną wykonania 5, 2 opcje call z ceną wykonania 5 i 3 opcje call z ceną wykonania 9 oraz sprzedać 4 opcje call z ceną wykonania 7.
Ćwiczenie 12.3
W dniu 1.09.2004 opcja OW20I4170 kosztowała 580 zł, a opcja OW20U4170 220 zł, natomiast
indeks WIG20 osiągnął 1730,87 pkt.
Dniem rozliczenia był 17.09.2004. Wyznacz (w oparciu o parytet kupna-sprzedaży) intensywność oprocentowania.
Uwaga: należy uwzględnić mnożnik 10 zł za 1 punkt indeksu.
Rozwiązanie. Z treści zadania wynika, że
Ponadto cena wykonania wynosi ![]() ,
a czas życia kontraktu 16 dni. Z zasady parytetu wynika, że
,
a czas życia kontraktu 16 dni. Z zasady parytetu wynika, że
Po wstawieniu powyższych danych otrzymujemy:
Odpowiedź.
Intensywność oprocentowania wyniosła 6,9%.