Zagadnienia
7. Analiza instrumentów dłużnych – cd
7.1. Wewnętrzna stopa zwrotu
7.1.1. Definicja 
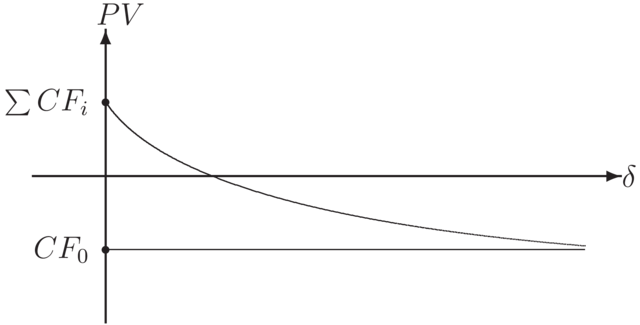
Rozważmy ciąg płatności ![]() mających miejsce odpowiednio w momentach
mających miejsce odpowiednio w momentach
![]() . Na przykład
. Na przykład![]() – zakup obligacji (
– zakup obligacji (![]() ),
),![]() – odsetki (kupony)
– odsetki (kupony) ![]() (
(![]() ),
),![]() – odsetki i wykup obligacji (
– odsetki i wykup obligacji (![]() ).
).
Dla płaskiej struktury terminowej mamy
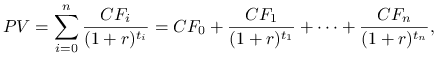 |
lub jeśli zastąpimy stopę procentową ![]() intensywnością
intensywnością ![]()
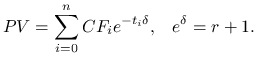 |
Pytanie: Przy jakiej stałej stopie procentowej ![]() (intensywności
(intensywności ![]() ) inwestycja jest opłacalna,
tzn.
) inwestycja jest opłacalna,
tzn. ![]() ?
?
Aby odpowiedzieć na to pytanie, wprowadza się pojęcie wewnętrznej stopy zwrotu.
Definicja 7.1
Wewnętrzną stopą zwrotu – ![]() (Internal Rate of Return)
nazywamy dodatni pierwiastek
(Internal Rate of Return)
nazywamy dodatni pierwiastek ![]() ,,równania wartości”
,,równania wartości”
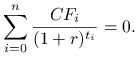 |
Natomiast wewnętrzną intensywością nazywamy dodatnią liczbę ![]() , dla której
, dla której
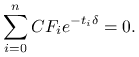 |
Jak łatwo zauważyć, wewnętrzna stopa zwrotu, to taka stopa procentowa, przy której
wartość obecna wpływów z inwestycji jest równa wartości obecnej
nakładów inwestycyjnych. Podobnie wewnętrzna intensywność, to taka intensywność oprocentowania,
przy której
wartość obecna wpływów z inwestycji jest równa wartości obecnej
nakładów inwestycyjnych.
Oczywiście obie te wielkości są związane zależnością
Zilustrujemy definicje na przykładzie.
Przykład 7.1
Rozważmy pięcioletni projekt
inwestycyjny:
| Rok | Nakłady | Przychody | |
| 0 | 5000 | 0 | -5000 |
| 1 | 2000 | 0 | -2000 |
| 2 | 1000 | 2000 | 1000 |
| 3 | 1000 | 3000 | 2000 |
| 4 | 1000 | 4000 | 3000 |
| 5 | 1000 | 5000 | 4000 |
Zgodnie z danymi z tabelki mamy
Jedynym dodatnim miejscem zerowym jest 0,10193. Zatem
![]() .
.
7.1.2. Istnienie 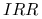
W ogólnym przypadku funkcja ![]() może nie mieć miejsc zerowych lub może się zerować
w kilku punktach.
może nie mieć miejsc zerowych lub może się zerować
w kilku punktach.
Rozważmy następujący przykład:
Inwestor wpłaca 100 natychmiast i 132 na
koniec dwóch lat w zamian za 230 otrzymane na koniec pierwszego roku.
Równanie wartości dla tej transakcji ma postać
lub
Po sprowadzeniu do postaci iloczynu mamy
Stąd stopą zwrotu jest ![]() lub
lub ![]() .
.
Wprawdzie nie jest rzeczą łatwą pogodzić się z faktem, że istnieją
transakcje z wieloma stopami zwrotu, jednak gdy zaobserwujemy, że funkcja
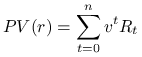 po pomnożeniu przez
po pomnożeniu przez ![]() jest
wielomianem
jest
wielomianem ![]() -tego stopnia zmiennej
-tego stopnia zmiennej ![]() ,
to staje się oczywiste, że
posiada ona – licząc pierwiastki
zespolone i pierwiastki wielokrotne –
,
to staje się oczywiste, że
posiada ona – licząc pierwiastki
zespolone i pierwiastki wielokrotne – ![]() miejsc zerowych.
miejsc zerowych.
Można sobie wyobrazić przypadki jeszcze bardziej niezwykłe:
Przykład 7.2
Inwestor A może pożyczyć 1000 od inwestora B na rok na 8%
oraz natychmiast zainwestować tę kwotę na rok na 10%. Jaka jest stopa
zwrotu inwestora A?
Odpowiedź. Zysk inwestora A w ciągu roku wynosi 20, ale kwota, którą zainwestował rzeczywiście A, wynosi 0. Tak więc jego stopa zwrotu jest nieskończona.
Przykład 7.3
Jaka jest stopa zwrotu z transakcji, w której inwestor płaci
100 natychmiast oraz 101 na końcu dwóch lat
w zamian za 200 otrzymane na koniec roku?
Odpowiedź. Równaniem wartości jest
co oznacza, że
W tym przypadku wewnętrzna stopa zwrotu nie istnieje.
Pokażemy, że dla w miarę naturalnych ograniczeń na przepływy gotówki ![]() istnieje.
Wystarczy, że
suma wypłat przewyższa sumę wpłat i pierwsza jest wpłata.
istnieje.
Wystarczy, że
suma wypłat przewyższa sumę wpłat i pierwsza jest wpłata.
Lemat 7.1
Jeżeli ![]() i
i ![]() to istnieje
to istnieje ![]() .
.
Dowód.
Rozważmy funkcję ![]()
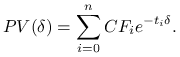 |
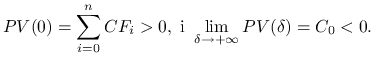 |
Funkcja ![]() jest ciągła i ponadto zmienia znak. Zatem,
musi istnieć punkt, w ktorym przyjmuje wartość zero
.
jest ciągła i ponadto zmienia znak. Zatem,
musi istnieć punkt, w ktorym przyjmuje wartość zero
.
Teza lematu pozostanie prawdziwa, gdy pierwszy przepływ gotówki (wpłata) ma miejsce w momencie ![]() .
.
Lemat 7.2
Jeżeli ![]() ,
, ![]() i
i ![]() to istnieje
to istnieje ![]() .
.
Dowód patrz ćwiczenie 7.1
7.1.3. Jednoznaczność 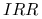
Warunki gwarantujące jednoznaczność nie są już tak oczywiste. Najprostszy przypadek to ,,najpierw wpłaty, a potem wypłaty”. W szczególności obejmuje to przypadek inwestycji w obligacje, kiedy mamy jedną wpłatę, a następnie same wypłaty.
Lemat 7.3
Jeżeli ![]() ,
, ![]() i
i ![]() to istnieje
dokładnie jedna
to istnieje
dokładnie jedna ![]() .
.
Dowód.
Niech ![]() ,,rozdziela” wpłaty i wypłaty
,,rozdziela” wpłaty i wypłaty
Wyłączamy czynnik wykładniczy ![]() z
z ![]() .
.
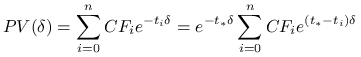 |
Następnie rozkładamy sumę na część dodatnią i ujemną. Zauważmy, że funkcja
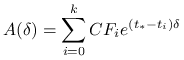 |
jest ściśle malejąca. Rzeczywiście dla ![]()
![]() i
i ![]() . Ponadto
. Ponadto
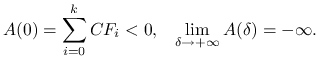 |
Również funkcja
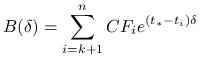 |
jest ściśle malejąca. Rzeczywiście dla ![]()
![]() i
i ![]() . Ponadto
. Ponadto
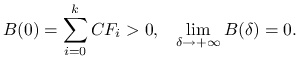 |
Zatem funkcja ![]() jest ciągła, ściśle malejąca i zmienia znak
jest ciągła, ściśle malejąca i zmienia znak
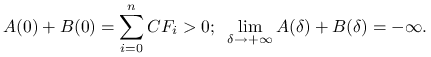 |
Ponieważ czynnik wykładniczy nigdzie się nie zeruje, to istnieje dokładnie jedno miejsce zerowe funkcji ![]() .
.
Powyższy lemat można uogólnić na przypadek, gdy pierwsza wpłata następuje po czasie ![]() .
.
Lemat 7.4
Jeżeli ![]() ,
, ![]() ,
, ![]() i
i ![]() to istnieje
dokładnie jedna
to istnieje
dokładnie jedna ![]() .
.
Bardziej skomplikowany przypadek to ,,jedna zmiana znaku skumulowanego przepływu”.
Oznaczmy przez ![]() skumulowany przepływ.
skumulowany przepływ.
Lemat 7.5
Jeżeli ![]() , dla
, dla ![]() i
i ![]() , dla
, dla ![]() i ponadto
i ponadto ![]() są wymierne,
to istnieje dokładnie jedna
są wymierne,
to istnieje dokładnie jedna ![]() .
.
Dowód.
Niech ![]() wspólny mianownik
wspólny mianownik ![]() .
Oznaczmy przez
.
Oznaczmy przez ![]() przepływ gotówki w momencie
przepływ gotówki w momencie ![]() .
. ![]() .
.
![C_{j}=\left\{\begin{array}[]{ccc}CF_{i}&\mbox{ gdy }&t_{i}=\frac{j}{N}\\
0&\mbox{ gdy }&t_{i}\neq\frac{j}{N}\end{array}\right.](wyklady/rka/mi/mi698.png) |
Zaczniemy od dowodu pomocniczego faktu.
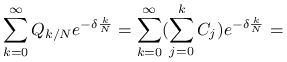 |
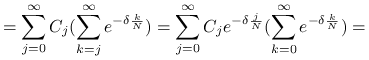 |
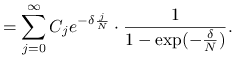 |
Zatem, gdy
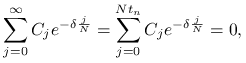 |
to
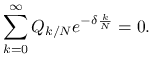 |
Dalej powtarzamy rozumownie z poprzedniego lematu i pokazujemy, że istnieje dokładnie jedna ![]() .
.
7.1.4. Kryterium inwestycyjne oparte na 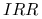
Załóżmy, że istnieje dokładnie jedna ![]() ,
,
![]() i
i ![]() . Możemy wówczas przeformułować
kryterium inwestycyjne oparte na
. Możemy wówczas przeformułować
kryterium inwestycyjne oparte na ![]() (2.1.4)
obliczonej dla płaskiej struktury terminowej. Niech
(2.1.4)
obliczonej dla płaskiej struktury terminowej. Niech
![]() – czynnik dyskontujący.
– czynnik dyskontujący.
Lemat 7.6
Jeżeli ![]() , to inwestycja jest opłacalna, a gdy
, to inwestycja jest opłacalna, a gdy ![]() , to nieopłacalna.
, to nieopłacalna.
Dowód.![]() zmienia znak w
zmienia znak w ![]() z ,,+” na ,,–”. Zatem gdy
z ,,+” na ,,–”. Zatem gdy
![]() , to
, to ![]() , a gdy
, a gdy ![]() , to
, to ![]() .
.
Uwaga. Gdy ![]() to
to ![]() wyznacza tzw. ,,margines bezpieczeństwa”.
wyznacza tzw. ,,margines bezpieczeństwa”.
Gdy ![]() nie jest wyznaczone jednoznacznie (istnieje kilka miejsc zerowych), ale
nie jest wyznaczone jednoznacznie (istnieje kilka miejsc zerowych), ale
![]() i
i ![]() , to można sformułować jedynie dużo słabsze kryterium:
, to można sformułować jedynie dużo słabsze kryterium:
Jeżeli ![]() , to inwestycja jest opłacalna, a gdy
, to inwestycja jest opłacalna, a gdy ![]() , to nieopłacalna.
, to nieopłacalna.
Przykład 7.4
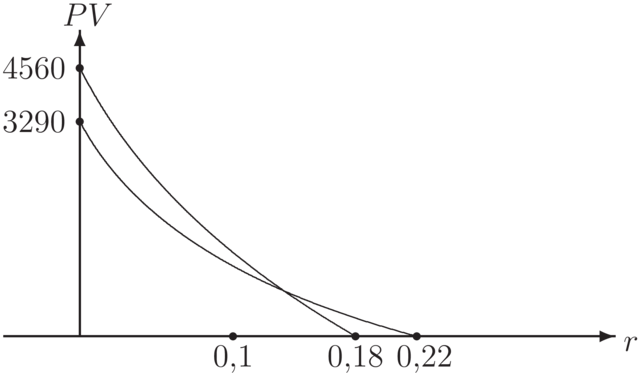
Rozważmy dwa wykluczające się projekty. W projekcie A nakłady
inwestycyjne wynoszą 7000 zł, natomiast wpływy 3430 zł, płatne na koniec każdego
z trzech lat. W projekcie B nakłady inwestycyjne wynoszą 12000 zł, a wpływy 5520 zł,
płatne na koniec każdego z trzech lat. Przy założeniu, że koszt
kapitału wynosi 10% rocznie (rynkowa stopa procentowa),
stosując kryterium PV oraz ![]() ,
rozstrzygnąć, który projekt należy wybrać.
,
rozstrzygnąć, który projekt należy wybrać.
Rozwiązanie.
Dla projektu A mamy ![]() , a dla projektu B
, a dla projektu B ![]() .
Obie te stopy są wyższe od stopy rynkowej, zatem obie inwestycje są opłacalne.
Na pytanie, którą z nich wybrać, nie ma jednoznacznej odpowiedzi.
Inwestycja A ma wyższą wewnętrzną stopę zwrotu, czyli większy margines bezpieczeństwa.
Za to inwestycja B ma wyższą wartość obecną. Rzeczywiście dla
.
Obie te stopy są wyższe od stopy rynkowej, zatem obie inwestycje są opłacalne.
Na pytanie, którą z nich wybrać, nie ma jednoznacznej odpowiedzi.
Inwestycja A ma wyższą wewnętrzną stopę zwrotu, czyli większy margines bezpieczeństwa.
Za to inwestycja B ma wyższą wartość obecną. Rzeczywiście dla ![]() mamy
mamy
![]() i
i ![]() .
Oznacza to, że gdy porównujemy dwie opłacalne inwestycje, to nasze kryteria
mogą dawać sprzeczne wnioski
.
.
Oznacza to, że gdy porównujemy dwie opłacalne inwestycje, to nasze kryteria
mogą dawać sprzeczne wnioski
.
7.1.5. 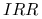 a
a 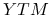
Rozważmy obligację, z której ![]() krotnie wypłacane są odsetki (obligacja
krotnie wypłacane są odsetki (obligacja ![]() -kuponowa),
co daje
-kuponowa),
co daje ![]() przepływów pieniężnych.
Niech
przepływów pieniężnych.
Niech ![]() – cena zakupu,
– cena zakupu,
![]() – kupony,
– kupony,
![]() – ostatni kupon i kwota otrzymana po wykupieniu obligacji.
Kolejne przepływy gotówki następują, odpowiednio, po czasie
– ostatni kupon i kwota otrzymana po wykupieniu obligacji.
Kolejne przepływy gotówki następują, odpowiednio, po czasie ![]() .
.
Dla takiej obligacji stopa zwrotu liczona do momentu zapadalności (![]() ) jest wyznaczona przez równanie
) jest wyznaczona przez równanie
Lub po podzieleniu przez ![]()
To samo równanie wyznacza wewnętrzną stopę zwrotu.
Wniosek 7.1
Ponadto spełnione są założenia lematu 2.2.3. Zatem ![]() jest wyznaczona jednoznacznie.
jest wyznaczona jednoznacznie.
7.1.6. Rzeczywista roczna stopa oprocentowania
Wewnętrzna stopa zwrotu znalazła swoje miejsce w obowiązujących w Polsce aktach prawnych
dotyczących kredytów. W ustawie o kredycie konsumenckim ([45, 46])
ustawodawca wprowadził wymóg informowania kredytobiorcy o
,,rzeczywistej rocznej stopie oprocentowania”, którą dla kredytów o stałym
oprocentowaniu wyznacza się jako wewnętrzną stopę
zwrotu dla wszystkich przepływów gotówki wynikających z danej umowy kredytowej.
Zatem jest to stopa procentowa ![]() , która spełnia następujące równanie
, która spełnia następujące równanie
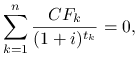 |
gdzie,![]() – numer kolejnego przepływu gotówki;
– numer kolejnego przepływu gotówki;![]() – czas wyrażony w latach, pomiędzy pierwszą wypłatą i
– czas wyrażony w latach, pomiędzy pierwszą wypłatą i ![]() -tym przepływem gotówki (
-tym przepływem gotówki (![]() ),
wyznaczony zgodnie z zasadą ,,dokładnej liczby dni” (patrz podrozdział 1.3.8);
),
wyznaczony zgodnie z zasadą ,,dokładnej liczby dni” (patrz podrozdział 1.3.8);![]() –
– ![]() -ty przepływ gotówki;
-ty przepływ gotówki;
Transze kredytu (![]() ) bierzemy ze znakiem minus, a raty kredytowe (
) bierzemy ze znakiem minus, a raty kredytowe (![]() ), zapłacone odsetki
), zapłacone odsetki ![]() ,
prowizje i inne opłaty (
,
prowizje i inne opłaty (![]() ) ze znakiem plus.
) ze znakiem plus.
Zgodnie z ustawą, rzeczywistą roczną stopę oprocentowania podaje się z dokładnością co najmniej do 1 promila.
7.1.7. Uogólnienia
1. Przypadek nieskończonej liczby płatności.
Równanie wartości ma postać
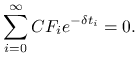 |
Zadanie jest dobrze postawione, gdy szereg jest zbieżny.
2. Przypadek ciągłego strumienia płatności.
Równanie wartości ma postać
gdzie: ![]() cena (koszt inwestycji) (
cena (koszt inwestycji) (![]() ),
), ![]() gęstość płatności.
gęstość płatności.
Oznaczmy przez ![]() skumulowany przepływ gotówki
skumulowany przepływ gotówki
Lemat 7.7
Jeżeli ![]() , dla
, dla ![]() i
i ![]() , dla
, dla ![]() i ponadto funkcja
i ponadto funkcja ![]() jest ograniczona i
jest ograniczona i ![]() ,
to istnieje dokładnie jedna
,
to istnieje dokładnie jedna ![]() .
.
Dowód.
Rozważmy funkcję ![]() ,
,
Jak łatwo zauważyć, zmienia ona znak ![]() i
i ![]() . Ponieważ jest ciągła,
to posiada miejsca zerowe.
. Ponieważ jest ciągła,
to posiada miejsca zerowe.
Po scałkowaniu przez części otrzymamy
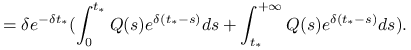 |
Ponieważ obie otrzymane całki są funkcjami malejącymi zmiennej ![]() , to
, to ![]() zeruje się tylko w jednym punkcie.
zeruje się tylko w jednym punkcie.
7.2. Ćwiczenia
Ćwiczenie 7.1
Udowodnić lemat 7.2.
Rozwiązanie.
Mamy ![]() , zatem
, zatem
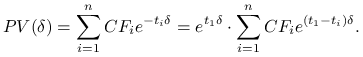 |
Oznaczmy drugi czynnik przez ![]() ,
,
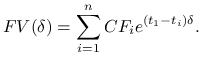 |
Ponieważ ![]() i
i ![]() , to
, to
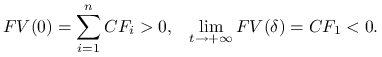 |
Funkcja ![]() jest ciągła i ponadto zmienia znak. Zatem,
istnieje punkt
jest ciągła i ponadto zmienia znak. Zatem,
istnieje punkt ![]() taki, że
taki, że ![]() .
.
Ćwiczenie 7.2
Udowodnić lemat 7.4.
Ćwiczenie 7.3
Zainwestowane 200 zł zwracają 120 zł po roku i 110 zł po dwóch latach. Wyznaczyć wewnętrzną stopę zwrotu dla tej inwestycji.
Rozwiązanie.
Równanie wartości ma postać
Skracamy współczynniki przez 10, podstawiamy ![]() i mnożymy równanie przez
i mnożymy równanie przez ![]() . Otrzymujemy równanie kwadratowe
. Otrzymujemy równanie kwadratowe
![]() wynosi 1024 czyli
wynosi 1024 czyli ![]() . Zatem pierwiastek większy od 1 to
. Zatem pierwiastek większy od 1 to
Czyli ![]() .
.
Odpowiedź.
Wewnętrzna stopa zwrotu rozpatrywanej inwestycji wynosi 10%.
Ćwiczenie 7.4
Która z poniższych inwestycji ma wyższą wewnętrzną stopę zwrotu?
Inwestycja A.
Zakup za 900 zł czteroletniej kuponowej obligacji o wartości nominalnej 1 000 zł
o stałym rocznym oprocentowaniu 20% (odsetki płatne po upływie kolejnego roku).
Inwestycja B.
Zakup za 800 zł zerokuponowej rocznej obligacji o wartości nominalnej 1 000 zł.
Rozwiązanie.
Wewnętrzna stopa zwrotu dla zerokuponowej rocznej obligacji o wartości nominalnej 1 000 zł i cenie 800 zł jest równa ,,zwykłej” stopie zwrotu i wynosi
Wyznaczamy Present Value inwestycji A dla ![]() .
.
Ponieważ ![]() jest funkcją malejącą to jej miejsce zerowe (
jest funkcją malejącą to jej miejsce zerowe (![]() ) leży na lewo od 0,25.
) leży na lewo od 0,25.
Odpowiedź.
Inwestycja B ma wyższą wewnętrzną stopę zwrotu.
Ćwiczenie 7.5
Kredytobiorca otrzymał kredyt 10 tys. zł wypłacony w dwóch równych transzach w odstępie rocznym.
W kolejnych latach kredytobiorca spłacił kredyt w czterech równych ratach po 3000 zł.
Spłaty miały miejsce po dwóch, trzech, czterech i pięciu latach od dnia
wypłaty pierwszej transzy. Ponadto przy wypłacie pierwszej transzy pobrano prowizję
w wysokości 500 zł. Ile wyniosła rzeczywista roczna stopa oprocentowania?
Rozwiązanie.
Mamy sześć przepływów gotówki ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Z lematu 2.2.3 wynika, że dla powyższych przepływów gotówki wewnętrzna stopa zwrotu,
a więc i rzeczywista roczna stopa oprocentowania ![]() są wyznaczone jednoznacznie.
Zatem
są wyznaczone jednoznacznie.
Zatem ![]() jest jedynym dodatnim pierwiastkiem równania
jest jedynym dodatnim pierwiastkiem równania
Po jego rozwiązaniu otrzymujemy
Odpowiedź.
Rzeczywista roczna stopa oprocentowania wynosi 8,3%.
Ćwiczenie 7.6
Sklep z artykułami gospodarstwa domowego proponuje swoim klientom ,,kredyt 0%”.
Należność za nabyty towar klient płaci w 12 równych miesięcznych ratach.
Ponadto za udzielenie kredytu pobierana jest prowizja, która wynosi 5% kwoty kredytu.
Wiedząc, że pierwsza rata ma miejsce po miesiącu od zawarcia umowy kredytowej (i zakupu towaru), a prowizja
jest pobierana w dniu zawarcia umowy, wyznacz rzeczywistą roczną stopę oprocentowania.
Rozwiązanie.
Mamy trzynaście przepływów gotówki ![]() . Dla uproszczenia przyjmiemy zasadę równych miesięcy
. Dla uproszczenia przyjmiemy zasadę równych miesięcy ![]() .
Niech
.
Niech ![]() oznacza kwotę kredytu.
oznacza kwotę kredytu.
Zatem rzeczywista roczna stopa oprocentowania ![]() jest jedynym dodatnim pierwiastkiem równania
jest jedynym dodatnim pierwiastkiem równania
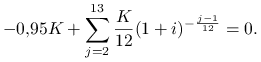 |
Po jego rozwiązaniu otrzymujemy
Odpowiedź.
Rzeczywista roczna stopa oprocentowania wynosi 10%.
Ćwiczenie 7.7
Inwestor zakupił za 100 JM rentę o ciągłym stałym strumieniu płatności o gęstości 10 w skali roku. Płatności zaczną się za rok i będą trwały nieprzerwanie 11 lat. Wyznaczyć wewnętrzną stopę zwrotu.
Rozwiązanie.
Równanie wartości ma postać
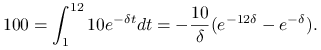 |
Jego pierwiastek to ![]() .
.
Zatem ![]() .
.
Odpowiedź.
Wewnętrzna intensywnośc wynosi 0,0148, a wewnętrzna stopa zwrotu 0,0149.