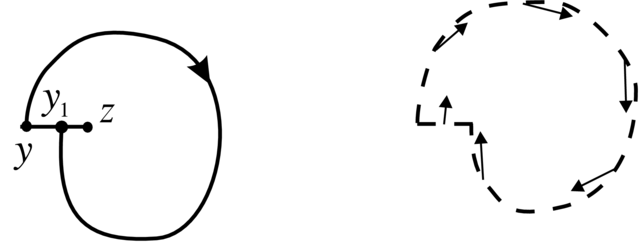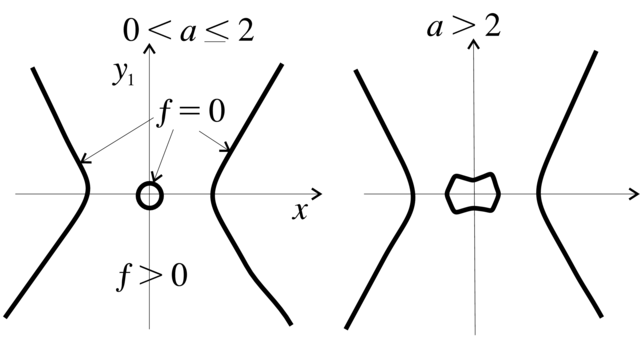Zagadnienia
2. Portrety fazowe autonomicznych pól wektorowych
Definicja 2.1.Portret fazowy autonomicznego pola
wektorowego ![]() na rozmaitości
na rozmaitości ![]() to rozbicie przestrzeni fazowej
to rozbicie przestrzeni fazowej ![]() na krzywe fazowe tego pola.
na krzywe fazowe tego pola.
Krzywe fazowe są trzech typów:
(i) punkty równowagi, czyli zdegenerowane krzywe odpowiadające stałym rozwiązaniom;
(ii) włożone odcinki (ograniczone lub nieograniczone), czyli
obrazy ![]() rozwiązań
rozwiązań ![]() , które są włożeniami;
, które są włożeniami;
(iii) zamknięte krzywe fazowe (włożone okręgi), odpowiadające okresowym rozwiązaniom ![]()
| (2.1) |
gdzie ![]() jest okresem rozwiązania (zakładamy, że jest
to minimalny okres spełniający (2.1)).
jest okresem rozwiązania (zakładamy, że jest
to minimalny okres spełniający (2.1)).
W całym tym rozdziale rozważamy tylko autonomiczne pola wektorowe; dlatego też będziemy opuszczali przmiotnik `autonomiczne'.
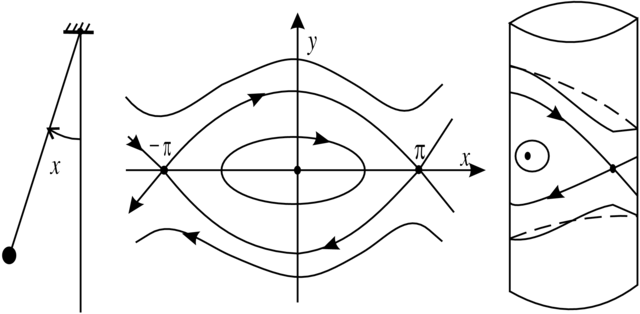
Przykład 2.2 (Wahadło Matematyczne). Jest to następujący układ
na przestrzeni fazowej ![]() (walec).
(walec).
Łatwo sprawdzić, że funkcja
| (2.2) |
jest całką pierwszą tego układu, tj. ![]() Odnotujmy następujące własności funkcji
Odnotujmy następujące własności funkcji ![]()
–punkt ![]() jest punktem absolutnego minimum i
jest punktem absolutnego minimum i ![]()
–punkt ![]() jest punktem siodłowym i
jest punktem siodłowym i ![]()
–![]() przy
przy ![]()
Łatwo też sprawdzić, że oprócz wskazanych wyżej punktów równowagi mamy dwie krzywe fazowe typu (ii); są to
separatrysy siodła ![]() leżące w poziomicy
leżące w poziomicy ![]() Pozostałe krzywe fazowe są zamknięte i można je podzielić na dwie grupy: (a) wokół punktu równowagi
Pozostałe krzywe fazowe są zamknięte i można je podzielić na dwie grupy: (a) wokół punktu równowagi
![]() (odpowiadające wahaniom o ograniczonej
amplitudzie) i (b) obiegające walec (one odpowiadają kręceniu
się wahadła wokół punktu zaczepienia).
(odpowiadające wahaniom o ograniczonej
amplitudzie) i (b) obiegające walec (one odpowiadają kręceniu
się wahadła wokół punktu zaczepienia).
Możemy policzyć okresy powyższych rozwiązań okresowych leżących na poziomicy ![]() całki pierwszej. Mamy
całki pierwszej. Mamy ![]() gdzie
gdzie ![]() wyznaczamy ze wzoru (2.2):
wyznaczamy ze wzoru (2.2): ![]() Zatem w
przypadku (a) mamy
Zatem w
przypadku (a) mamy
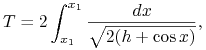 |
gdzie ![]() to dwa zera funkcji
to dwa zera funkcji ![]() Tutaj całka od
Tutaj całka od ![]() do
do ![]() daje czas pozostawania trajektorii w obszarze
daje czas pozostawania trajektorii w obszarze ![]() ale, z
uwagi na symetrię, jest to dokładnie połowa okresu. W przypadku (b)
mamy
ale, z
uwagi na symetrię, jest to dokładnie połowa okresu. W przypadku (b)
mamy
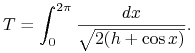 |
Niestety, powyższe całki nie dają się policzyć w terminach
elementarnych funkcji. Rzeczywiście, po podstawieniu ![]() (z
(z ![]() dostajemy
dostajemy
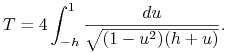 |
Całka po prawej stronie ostatniej równości to tzw. całka eliptyczna definiująca pewną funkcję eliptyczną6Całki i funkcje eliptyczne pojawiają się bardzo często w równaniach różniczkowych mechaniki klasycznej (patrz [4]. (Zadanie 2.44).
Zauważmy jeszcze, że zamknięte krzywe fazowe w tym przykładzie są nieizolowane, występują w całych rodzinach.
2.1. Rozwiązania okresowe
Zamknięte krzywe fazowe są też nazywane trajektoriami okresowymi lub orbitami okresowymi. W Przykładzie 2.2 występują one w całych rodzinach, ale istnieją też trajektorie okresowe izolowane.
Definicja 2.3.Cyklem granicznym autonomicznego pola wektorowego nazywamy izolowaną zamkniętą krzywą fazową tego pola.
Punkt równowagi takiego pola, który jest otoczony nieizolowanymi zamkniętymi krzywymi fazowymi, nazywa się centrum.
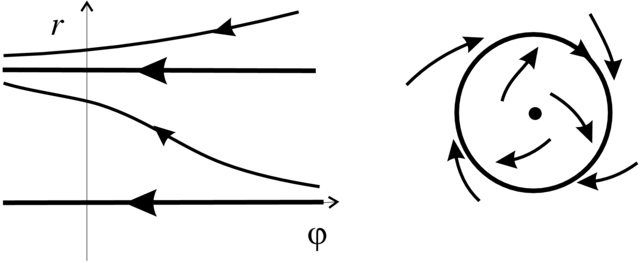
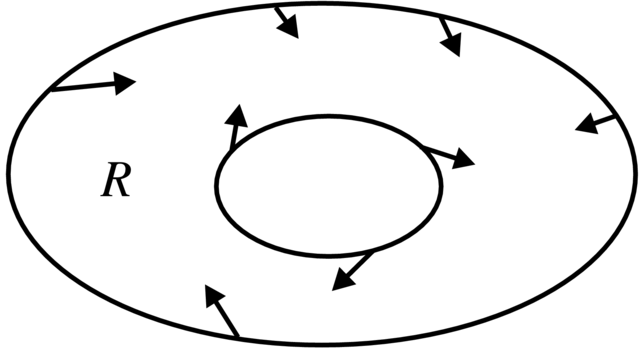
Przykład 2.4. Rozważmy układ
Wygodnie jest badać ten układ w biegunowym układzie współrzędnych ![]()
(Zadanie 2.46). Widać, że rozwiązania startujące z ![]() rosną z czasem do
rosną z czasem do ![]() a rozwiązania
startujące z
a rozwiązania
startujące z ![]() maleją do
maleją do ![]() Rozwiązanie startujące z
Rozwiązanie startujące z ![]() jest stałe i odpowiada izolowanemu okresowemu rozwiązaniu na płaszczyźnie
jest stałe i odpowiada izolowanemu okresowemu rozwiązaniu na płaszczyźnie ![]() (patrz Rysunek 2.2).
(patrz Rysunek 2.2).
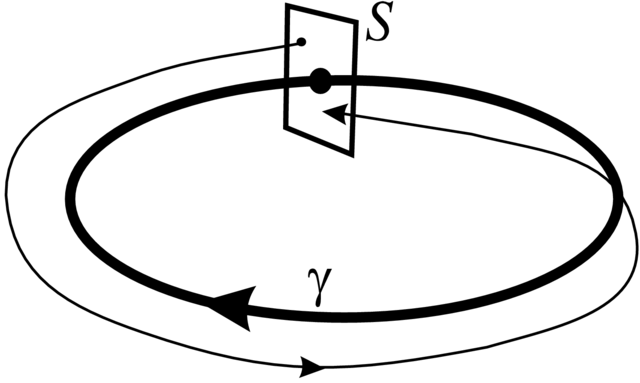
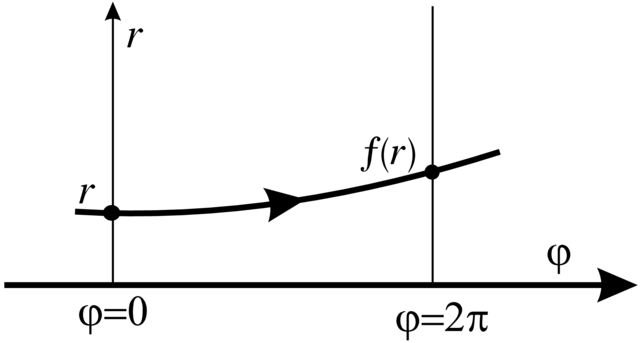
Definicja 2.5. Niech ![]() będzie zamkniętą krzywą fazową pewnego pola wektorowego w
będzie zamkniętą krzywą fazową pewnego pola wektorowego w ![]() Weźmy kiełek
Weźmy kiełek ![]() (od `section' czyli cięcie) hiperpłaszczyzny transwersalnej
(tj. pod niezerowym kątem) do
(od `section' czyli cięcie) hiperpłaszczyzny transwersalnej
(tj. pod niezerowym kątem) do ![]() w pewnym punkcie
w pewnym punkcie ![]() Z punktów
Z punktów ![]() startuje rozwiązanie
startuje rozwiązanie ![]() które po pewnym czasie
które po pewnym czasie ![]() znowu trafia w
znowu trafia w ![]()
![]() Powstające w ten sposób odwzorowanie
Powstające w ten sposób odwzorowanie
![]() (dyfeomorfizm z odpowiednią dziedziną):
(dyfeomorfizm z odpowiednią dziedziną):
nazywa się przekształceniem powrotu Poincarégo (patrz Rysunek 2.3).
W tej definicji występuje znaczna dowolność związana z
wyborem cięcia ![]() Okazuje się, że to nie stanowi wielkiego
problemu bo, jeśli
Okazuje się, że to nie stanowi wielkiego
problemu bo, jeśli ![]() jest
przekształceniem powrotu związanym z innym cięciem
jest
przekształceniem powrotu związanym z innym cięciem ![]() ,
to zachodzi następujący
,
to zachodzi następujący
Lemat 2.6.Dyfeomorfizmy ![]() i
i ![]() są sprzężone przy pomocy pewnego dyfeomorfizmu tej
samej klasy gładkości co
są sprzężone przy pomocy pewnego dyfeomorfizmu tej
samej klasy gładkości co ![]() i
i![]()
Dowód. Niech ![]() i
i ![]() będą naturalnymi przekształceniami `wzdłuż rozwiązań. Mamy
będą naturalnymi przekształceniami `wzdłuż rozwiązań. Mamy ![]() i
i ![]() ∎
∎
Cięcie ![]() możemy utożsamić z
możemy utożsamić z ![]() gdzie
gdzie ![]() i przekształcenie powrotu
definiuje nam kiełek dyfeomorfizmu
i przekształcenie powrotu
definiuje nam kiełek dyfeomorfizmu ![]() (bo
(bo
![]() ) postaci
) postaci
(Zadanie 2.47).
Definicja 2.7. Zamknięta krzywa fazowa ![]() jest hiperboliczna jeśli punkt stały
jest hiperboliczna jeśli punkt stały ![]() powyższgo dyfeomorfizmu
jest hiperboliczny, tzn.
powyższgo dyfeomorfizmu
jest hiperboliczny, tzn. ![]() dla
wartości własnych macierzy
dla
wartości własnych macierzy ![]()
Następujące dwa stwierdzenia są prostymi analogami Twierdzenia Lapunowa i Twierdzenia Hadamarda–Perrona.
Stwierdzenie 2.8.Jeśli ![]() dla wszystkich wartości własnych to
krzywa
dla wszystkich wartości własnych to
krzywa ![]() jest asymptotycznie stabilna, tzn. dowolne rozwiązanie
jest asymptotycznie stabilna, tzn. dowolne rozwiązanie ![]() startujące dostatecznie blisko
startujące dostatecznie blisko ![]() ma własność, że dist
ma własność, że dist![]() przy
przy ![]()
Stwierdzenie 2.9.Jeśli krzywa ![]() jest
hiperboliczna, to istnieją podrozmaitości
jest
hiperboliczna, to istnieją podrozmaitości ![]() (stabilna) i
(stabilna) i ![]() (niestabilna) takie, że dist
(niestabilna) takie, że dist![]() dla
dla ![]() i
i
![]() oraz dist
oraz dist![]() dla
dla ![]() i
i![]()
Bardziej interesujące chyba jest następujące
Stwierdzenie 2.10.Gdy ![]() i zarówno
sama rozmaitość jak i pole wektorowe
i zarówno
sama rozmaitość jak i pole wektorowe ![]() są
analityczne i
są
analityczne i ![]() jest zamkniętą krzywą fazową pola
jest zamkniętą krzywą fazową pola ![]() , to albo
, to albo ![]() jest cyklem granicznym
albo istnieje (jednoznaczna) całka pierwsza w otoczeniu krzywej
jest cyklem granicznym
albo istnieje (jednoznaczna) całka pierwsza w otoczeniu krzywej![]()
Dowód. W istocie tutaj trzeba udowodnić, że rozwiązania okresowe pola ![]() nie mogą się akumulować na krzywej
nie mogą się akumulować na krzywej ![]() To jest równoważne własności, że przekształcenie powrotu Poincarégo
To jest równoważne własności, że przekształcenie powrotu Poincarégo ![]() ma albo izolowany punkt stały w
ma albo izolowany punkt stały w ![]() albo
albo ![]() Ale to wynika analityczności funkcji
Ale to wynika analityczności funkcji ![]() (przy założeniu, że cięcie
(przy założeniu, że cięcie ![]() jest analityczne) i standardowych własności funkcji analitycznych.
jest analityczne) i standardowych własności funkcji analitycznych.
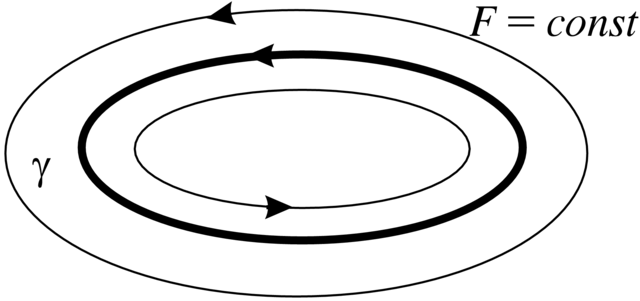
W przypadku ![]() wszystkie krzywe fazowe w otoczeniu
wszystkie krzywe fazowe w otoczeniu ![]() są
zamknięte i są one poziomicami pewnej całki pierwszej
są
zamknięte i są one poziomicami pewnej całki pierwszej ![]() dla pola
wektorowego (Rysunek 2.4). ∎
dla pola
wektorowego (Rysunek 2.4). ∎
To stwierdzenie ma analog dla punktu osobliwego ![]() analitycznego pola
wektorowego w przypadku, gdy część liniowa pola ma
nierzeczywiste wartości własne, tj.
analitycznego pola
wektorowego w przypadku, gdy część liniowa pola ma
nierzeczywiste wartości własne, tj.
| (2.3) |
Stwierdzenie 2.11.W przypadku analitycznego pola typu
(2.3) na płaszczyźnie zachodzi jedna z dwóch możliwości:
albo punkt ![]() jest ogniskiem (stabilnym lub
niestabilnym) albo istnieje (jednoznaczna) całka pierwsza w otoczeniu tego
punktu (czyli punkt
jest ogniskiem (stabilnym lub
niestabilnym) albo istnieje (jednoznaczna) całka pierwsza w otoczeniu tego
punktu (czyli punkt ![]() jest centrum).
jest centrum).
Dowód. Trzeba przejść do biegunowego układu współrzędnych ![]() . Dostaniemy wtedy
. Dostaniemy wtedy
| (2.4) |
gdzie ![]() i
i ![]() rozwijają się w zbieżny szeregi potęgowe od
rozwijają się w zbieżny szeregi potęgowe od ![]() ze współczynnikami będącymi
wielomianami trygonometrycznymi od
ze współczynnikami będącymi
wielomianami trygonometrycznymi od ![]() (Zadanie 2.48). Krzywe
fazowe tego układu spełniają równanie różniczkowe
(Zadanie 2.48). Krzywe
fazowe tego układu spełniają równanie różniczkowe
| (2.5) |
Jego rozwiązania ![]() takie, że
takie, że ![]() zadają przekształcenie
zadają przekształcenie
które jest analogiem przekształcenia powrotu Poincarégo. W istocie
jest to przekształcenie powrotu dla pola (2.3) z półosi ![]() w
siebie (patrz Rysunek 2.5). Ze zbieżności szeregów reprezentujących
w
siebie (patrz Rysunek 2.5). Ze zbieżności szeregów reprezentujących ![]() i
i ![]() wynika, że przekształcenie
wynika, że przekształcenie ![]() jest analityczne.
jest analityczne.
Punkty stałe dyfeomorfizmu ![]() odpowiadają zamkniętym krzywym
fazowym pola (2.3). Tak jak i w dowodzie poprzedniego stwierdzenia, albo
odpowiadają zamkniętym krzywym
fazowym pola (2.3). Tak jak i w dowodzie poprzedniego stwierdzenia, albo ![]() jest izolowanym punktem stałym dla
jest izolowanym punktem stałym dla ![]() albo
albo ![]() i wtedy wszystkie
krzywe fazowe w otoczeniu
i wtedy wszystkie
krzywe fazowe w otoczeniu ![]() są zamknięte. ∎
są zamknięte. ∎
Przekształcenie powrotu Poincarégo ![]() rozwija się w szereg
rozwija się w szereg
| (2.6) |
Łatwo sprawdzić, że ![]() (Zadanie 2.49).
(Zadanie 2.49).
Lemat 2.12.Jeśli ![]() to
to ![]() i, ogólniej, jeśli
i, ogólniej, jeśli ![]() to
to![]()
Ten lemat jest konsekwencją Twierdzenia Poincarégo–Dulaca
(dowodzonego w Rozdziale 3.3.1) i dlatego go tutaj nie dowodzimy. Słuchacze mogą dowodzić go wykorzystując pewne własności
symetrii (względem zamiany ![]() funkcji
funkcji ![]() i
i ![]() w (2.4).
w (2.4).
Stąd wynika, że jeśli ![]() i
i
![]() (odpowiednio
(odpowiednio ![]() to punkt
to punkt ![]() jest ogniskiem stabilnym
(odpowiednio niestabilnym).
jest ogniskiem stabilnym
(odpowiednio niestabilnym).
Definicja 2.13. Wspólczynniki
nazywają się liczbami ogniskowymi Lapunowa–Poincarégo.
Uwaga 2.14. Liczby ogniskowe są ważnie przy badaniu tzw. małych cykli granicznych, tzn. które rodzą się z ogniska w przypadku, gdy pole wektorowe zależy od pewnych parametrów. Jednak są one trudne do policzenia. Poniżej podaję pewien sposób ich wyliczenia; ten sposób w istocie był wykorzystywany przez Lapunowa.
Zamiast współrzędnych rzeczywistych będziemy używać współrzędnych zespolonych ![]() i
i ![]()
![]() tak, że pole wektorowe zapisuje się w postaci jednego równania
zespolonego
tak, że pole wektorowe zapisuje się w postaci jednego równania
zespolonego
| (2.7) |
gdzie ![]() są zespolonymi stałymi. Zauważmy,
że część liniowa jest tu znacznie uproszczona; w szczególnoości,
są zespolonymi stałymi. Zauważmy,
że część liniowa jest tu znacznie uproszczona; w szczególnoości, ![]()
Będziemy poszukiwać całki pierwszej dla równania (2.7) w postaci
| (2.8) |
gdzie warunek rzeczywistości ![]() prowadzi do warunków
prowadzi do warunków ![]() Oczywiście, na ogół nie będzie całki pierwszej i
przeszkody do tego są związane z liczbami ogniskowymi
Lapunowa–Poincarégo.
Oczywiście, na ogół nie będzie całki pierwszej i
przeszkody do tego są związane z liczbami ogniskowymi
Lapunowa–Poincarégo.
Oczekiwana własność ![]() prowadzi do następującego układu równań algebraicznych
prowadzi do następującego układu równań algebraicznych
dla współczynników wielomianu ![]() przy wyrazach sześciennych.
Znajdujemy
przy wyrazach sześciennych.
Znajdujemy ![]() ,
, ![]() i
i ![]() (tu nie
ma przeszkód). Ale dla wyrazu przy
(tu nie
ma przeszkód). Ale dla wyrazu przy ![]() po zróżniczkowaniu funkcji (2.8), dostajemy
po zróżniczkowaniu funkcji (2.8), dostajemy
Widzimy, że aby ![]() (modulo wyrazy rzędu piątego), musi
zachodzić
(modulo wyrazy rzędu piątego), musi
zachodzić
spodziewamy się, że liczba ogniskowa ![]() jest proporcjonalna do
jest proporcjonalna do ![]()
Aby znaleźć stałą proporcjonalności, zauważmy, że ![]()
![]() oraz
oraz ![]() Zatem
Zatem
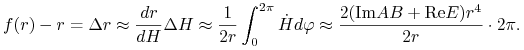 |
To daje
| (2.9) |
(Zadanie 2.50).
2.2. Kryterium Poincarégo–Bendixsona
Problem badania cykli granicznych okazuje się bardzo trudny. Swiadczy o tym następujący problem nierozwiązany do dziś.
Hipoteza 2.15 (Szesnasty Problem Hilberta). 7W istocie jest to druga część 16-go Problemu Hilberta. Pierwsza
część dotyczy liczby i położenia składowych spójnych (tzw. owali) dla rzeczywistych krzywych algebraicznych postaci ![]() . Tutaj problem jest w znacznym stopniu rozwiązany (z
odpowiednimi uogólnieniami). Podać oszacowanie w terminach stopni
wielomianów
. Tutaj problem jest w znacznym stopniu rozwiązany (z
odpowiednimi uogólnieniami). Podać oszacowanie w terminach stopni
wielomianów ![]() i
i ![]() dla liczby cykli granicznych wielomianowego pola
wektorowego postaci
dla liczby cykli granicznych wielomianowego pola
wektorowego postaci
| (2.10) |
Uwaga 2.16. Wiadomo, że liczba cykli granicznych dla
pojedynczego pola postaci (2.10) jest skończona (Yu. Ilyashenko i J.
Ecalle), ale nie wiadomo czy istnieje jej ograniczenie w terminach ![]() Są przykłady pól kwadratowych z 4 cyklami
granicznymi (Zadanie 2.51).
Są przykłady pól kwadratowych z 4 cyklami
granicznymi (Zadanie 2.51).
Dlatego ważne są konkretne metody pokazujące istnienie cykli granicznych lub ich brak. Prezentowane poniżej kryterium Poincarégo–Bendixsona gwarantuje nam istnienie przynajmniej jednego cyklu granicznego pod warunkiem, że pole wektorowe jest analityczne (patrz Stwierdzenie 2.10).
Załóżmy, że mamy pole wektorowe ![]() na płaszczyźnie
oraz obszar
na płaszczyźnie
oraz obszar ![]() typu pierścienia (jak
na Rysunku 2.6) o następujących własnościach:
typu pierścienia (jak
na Rysunku 2.6) o następujących własnościach:
(i) pole ![]() nie ma punktów równowagi w
nie ma punktów równowagi w ![]()
(ii) pole ![]() na brzegu
na brzegu ![]() pierścienia
pierścienia ![]() jest skierowane do wnętrza pierścienia.
jest skierowane do wnętrza pierścienia.
Twierdzenie 2.17 (Poincaré–Bendixson). Przy tych założeniach wewnątrz obszaru ![]() istnieje co
najmniej jedna zamknięta krzywa fazowa pola
istnieje co
najmniej jedna zamknięta krzywa fazowa pola ![]()
W dowodzie tego twierdzenia wykorzystuje się następujące ważne pojęcie w Układach Dynamicznych.
Definicja 2.18.Zbiorem ![]() granicznym punktu
granicznym punktu![]() oznaczanym przez
oznaczanym przez ![]() , względem potoku fazowego
, względem potoku fazowego ![]() (lub kaskady
(lub kaskady ![]() nazywamy zbiór punktów
skupienia dodatniej orbity tego punktu, czyli
nazywamy zbiór punktów
skupienia dodatniej orbity tego punktu, czyli
(lub ![]() (Zadanie 2.52).
(Zadanie 2.52).
W przypadku punktów skupienia ujemnej orbity punktu ![]() (tzn. gdy
(tzn. gdy ![]() lub
lub ![]() mówi się
o zbiorze
mówi się
o zbiorze ![]() granicznym punktu
granicznym punktu ![]()
Oczywiście przyciągający cykl graniczny jest zbiorem ![]() granicznym dla dowolnego punktu leżącego blisko tego cyklu. Istnieje
wersja Twierdzenia Poincarégo–Bendixsona używająca pojęcia
zbioru
granicznym dla dowolnego punktu leżącego blisko tego cyklu. Istnieje
wersja Twierdzenia Poincarégo–Bendixsona używająca pojęcia
zbioru ![]() granicznego dla potoku fazowego generowanego przez pole
wektorowego
granicznego dla potoku fazowego generowanego przez pole
wektorowego ![]() .
.
Twierdzenie 2.19.Jeśli dla pola wektorowego ![]() w
w![]() i punktu
i punktu ![]() zbiór
zbiór ![]() jest:
jest:
(a) ograniczony i
(b) nie zawiera punktów równowagi pola,
to ![]() jest zamkniętą krzywą fazową tego
pola.
jest zamkniętą krzywą fazową tego
pola.
Dowód. Niech ![]() Pokażemy, że
trajektoria pola przechodząca przez
Pokażemy, że
trajektoria pola przechodząca przez ![]() jest zamknięta.
jest zamknięta.
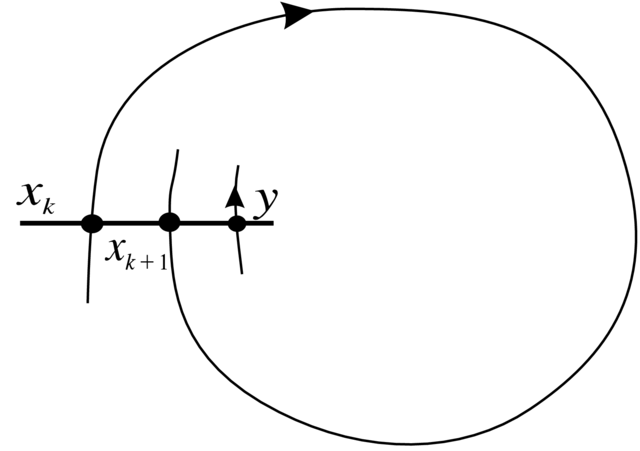
W tym celu wybierzmy lokalne cięcie (odcinek) ![]() prostopadłe do
prostopadłe do ![]() w
w ![]() Rozważmy punkty przecięcia
Rozważmy punkty przecięcia ![]()
![]() orbity
orbity ![]() z cięciem
z cięciem ![]() Z założenia takich punktów jest nieskończnie wiele
i możemy założyć, że ciąg
Z założenia takich punktów jest nieskończnie wiele
i możemy założyć, że ciąg ![]() jest monotoniczny na
jest monotoniczny na ![]() (tu korzystamy z faktu, że jesteśmy na płaszczyźnie) (Zadanie 2.53). Zatem mamy sytuację jak na Rysunku 2.7.
Zauważmy jeszcze, że cała orbita w przód
(tu korzystamy z faktu, że jesteśmy na płaszczyźnie) (Zadanie 2.53). Zatem mamy sytuację jak na Rysunku 2.7.
Zauważmy jeszcze, że cała orbita w przód ![]() punktu
punktu ![]() też leży w zbiorze
też leży w zbiorze ![]() zatem mamy
zatem mamy
Oczywiście ![]() jest zbiorem domkniętym, ograniczonym i bez
punktów równowagi pola
jest zbiorem domkniętym, ograniczonym i bez
punktów równowagi pola ![]()
Przypuśćmy, że krzywa ![]() nie jest zamkniętą
krzywą fazową. Wtedy
nie jest zamkniętą
krzywą fazową. Wtedy ![]() i istnieje punkt
skupienia
i istnieje punkt
skupienia ![]() trajektorii
trajektorii ![]() Znowu możemy wziąć cięcie
Znowu możemy wziąć cięcie ![]() prostopadłe do
prostopadłe do ![]() w
w ![]() i (ewentualnie zamieniając
i (ewentualnie zamieniając ![]() którymś z punktów
którymś z punktów ![]() przecięcia
przecięcia ![]() z
z ![]() ) uzyskamy sytuację jak na
Rysunku 2.8.
) uzyskamy sytuację jak na
Rysunku 2.8.
Teraz deformując nieznacznie kawałek trajektorii ![]() (od
(od ![]() do
do ![]() tak, aby nowa krzywa była ustawiona do pola
tak, aby nowa krzywa była ustawiona do pola ![]() pod kątem, dostaje się obszar
pod kątem, dostaje się obszar ![]() do którego
pole `wchodzi'. Ale to daje sprzeczność, bo musi zachodzić
do którego
pole `wchodzi'. Ale to daje sprzeczność, bo musi zachodzić ![]() a stąd, że
a stąd, że
zauważmy, że ![]() musi zawierać też punkty orbity
musi zawierać też punkty orbity ![]() punktu
punktu ![]() spoza
spoza ![]() ∎
∎
Dowód Twierdzenia 2.17. Bierzemy dowolny punkt ![]() Wtedy jego zbiór
Wtedy jego zbiór ![]() graniczny spełnia założenia Twierdzenia 2.19. ∎
graniczny spełnia założenia Twierdzenia 2.19. ∎
Przykład 2.20.8Ten przykład pochodzi z monografii “Modern
Geometry” Dubrovina, Novikova i Fomenko. Niestety tam nie
ma pewnych istotnych detali, które uzupełniłem. Ponadto układ Liénarda zwykle przyjmuje formy ![]()
![]() lub
lub ![]() Układ (2.11) po zamianie
Układ (2.11) po zamianie ![]() z
z ![]() sprowadza się do drugiej z nich. Rozważmy następujący przypadek tzw. układu Liénarda
sprowadza się do drugiej z nich. Rozważmy następujący przypadek tzw. układu Liénarda
| (2.11) |
gdzie ![]() ; w istocie chodzi o to, aby
; w istocie chodzi o to, aby ![]() była
nieparzysta,
była
nieparzysta, ![]() i
i ![]()
Zauważmy, że jedyny punkt równowagi ![]() jest
ogniskiemniestabilnym (z wartościami własnymi
jest
ogniskiemniestabilnym (z wartościami własnymi ![]() Wobec tego wybieramy wewnętrzny brzeg pierścienia
Wobec tego wybieramy wewnętrzny brzeg pierścienia
![]() (aby zastosować Twierdzenie 2.17) w postaci
(aby zastosować Twierdzenie 2.17) w postaci
dla małego ![]() (Zadanie 2.54).
(Zadanie 2.54).
Chciałoby się wybrać zewnętrzny brzeg w postaci dużego okręgu ![]() Niestety tożsamość
Niestety tożsamość
pokazuje, że w obszarze ![]() funkcja `kwadratu promienia'
funkcja `kwadratu promienia' ![]() zwiększa swoją wartość wzłuż
trajektorii pola. Szczęśliwie ten zły obszar jest mały.
zwiększa swoją wartość wzłuż
trajektorii pola. Szczęśliwie ten zły obszar jest mały.
Aby wszystko uściślić, rozważmy cztery obszary płaszczyzny
(I, II, III, IV), w których badamy ![]() Są one przedstawione na Rysunku 2.9, gdzie na granicy pomiędzy I i II
mamy
Są one przedstawione na Rysunku 2.9, gdzie na granicy pomiędzy I i II
mamy ![]() i na granicach pomiędzy II i III oraz pomiędzy III i
IV mamy
i na granicach pomiędzy II i III oraz pomiędzy III i
IV mamy ![]()
Startujemy z punktu ![]() takiego, że
takiego, że ![]() jest duże i
jest duże i ![]() Wchodzimy do obszaru I, gdzie
Wchodzimy do obszaru I, gdzie ![]() Tutaj
układ jest bliski układowi liniowemu
Tutaj
układ jest bliski układowi liniowemu ![]()
![]() i
nietrudno jest oszacować, że zmiana
i
nietrudno jest oszacować, że zmiana ![]() promienia
promienia ![]() w
obszarze I jest postaci
w
obszarze I jest postaci
gdzie ![]() i nie zależy od
i nie zależy od ![]()
Wkraczamy do obszaru II z promieniem ![]() Jest to
duży promień a zatem i
Jest to
duży promień a zatem i ![]() jest duże (bo
jest duże (bo ![]() jest ograniczone).
Tutaj krzywe fazowe spełniają równanie
jest ograniczone).
Tutaj krzywe fazowe spełniają równanie
i mamay oszacowanie
dla pewnej stałej ![]() niezależnej od
niezależnej od ![]()
Analogicznie jak w obszarze I dostajemy ![]() (gdzie
(gdzie ![]() i, analogicznie jak w obszarze II, dostajemy
i, analogicznie jak w obszarze II, dostajemy ![]() Sumując te przyrosty
dostajemy
Sumując te przyrosty
dostajemy
dla stałej ![]() niezależnej od
niezależnej od ![]()
Zatem promień ![]() średnio maleje i już teraz łatwo skonstruować zewnętrzny brzeg pierścienia
średnio maleje i już teraz łatwo skonstruować zewnętrzny brzeg pierścienia ![]() wystarczy lekko
przekrzywić trajektorię punktu
wystarczy lekko
przekrzywić trajektorię punktu ![]() i polączyć końce odcinkiem.
i polączyć końce odcinkiem.
Słuchacze mogą zapytać, dlaczego w twierdzeniu Poincarégo–Bendixsona obszar ![]() jest pierścieniem; może wystarczyłoby, aby był ograniczony i jednospójny (tj. bez dziury w środku). Otóż nie, i powód leży w następującym
twierdzeniu.
jest pierścieniem; może wystarczyłoby, aby był ograniczony i jednospójny (tj. bez dziury w środku). Otóż nie, i powód leży w następującym
twierdzeniu.
Twierdzenie 2.21.Wewnątrz obszaru ograniczonego przez zamkniętą krzywą fazową pola wektorowego na płaszczyźnie istnieje co najmniej jeden punkt osobliwy tego pola.
Dowód tego wyniku używa metod topologicznych, a dokładniej, pojęcia indeksu.
Definicja 2.22. Niech ![]() będzie polem wektorowym w
będzie polem wektorowym w ![]() i niech
i niech ![]() będzie zorientowaną krzywą taką, że
będzie zorientowaną krzywą taką, że
| (2.12) |
Indeksem ![]() pola
pola ![]() wzdłuż krzywej
wzdłuż krzywej![]() mazywamy liczbę obrotów wektora
mazywamy liczbę obrotów wektora ![]()
Jeśli ![]() jest izolowanym punktem osobliwym pola
jest izolowanym punktem osobliwym pola ![]() to indeksem
to indeksem ![]() pola
pola ![]() w punkcie
w punkcie ![]() nazywamy indeks
nazywamy indeks ![]() pola
pola ![]() wzdłuż okręgu
wzdłuż okręgu ![]() wokół
wokół ![]() o dostatecznie małym
promieniu
o dostatecznie małym
promieniu ![]() (i zorientowanego przeciwnie do ruchu wskazówek zegara, tj. dodatnio).9Pojęcie indeksu izolowanego punktu osobliwego
(i zorientowanego przeciwnie do ruchu wskazówek zegara, tj. dodatnio).9Pojęcie indeksu izolowanego punktu osobliwego ![]() pola wektorowego
pola wektorowego ![]() uogólnia się do przypadku pola w
uogólnia się do przypadku pola w ![]() Jest to
stopień odwzorowania
Jest to
stopień odwzorowania ![]() z małej sfery wokół
z małej sfery wokół ![]() do
do ![]()
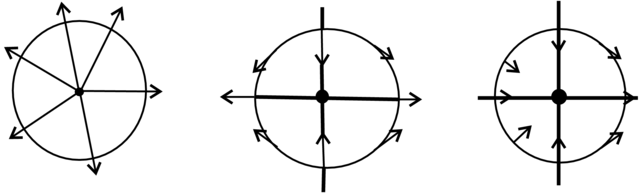
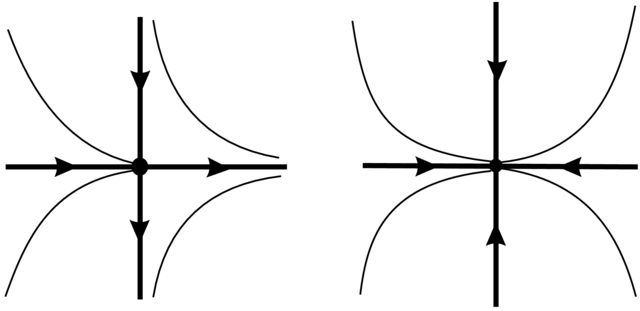
Przykłady 2.23. Dla pola ![]() mamy
mamy ![]() , dla pola
, dla pola ![]() mamay
mamay ![]() a dla pola
a dla pola ![]() mamay
mamay ![]() , patrz Rysunek 2.10 (Zadania 2.55 i 2.56).
, patrz Rysunek 2.10 (Zadania 2.55 i 2.56).
Stwierdzenie 2.24.Dla dodatnio zorientowanej krzywej ![]() mamy
mamy
gdzie sumowanie biegnie po punktach osobliwych pola wewnątrz
obszaru ograniczonego przez krzywą![]()
Dowód. Zauważmy, że odwzorowanie
jest funkcją ciągłą na przestrzeni par ![]() spełniających warunek (2.12). Ponieważ
zbiorem wartości tej funkcji są liczby całkowite, to indeks jest
lokalnie stały. W szczególności nie zależy od deformacji pola
i deformacji krzywej (w klasie (2.12); to uzasadnia definicję indeksu w
punkcie.
spełniających warunek (2.12). Ponieważ
zbiorem wartości tej funkcji są liczby całkowite, to indeks jest
lokalnie stały. W szczególności nie zależy od deformacji pola
i deformacji krzywej (w klasie (2.12); to uzasadnia definicję indeksu w
punkcie.
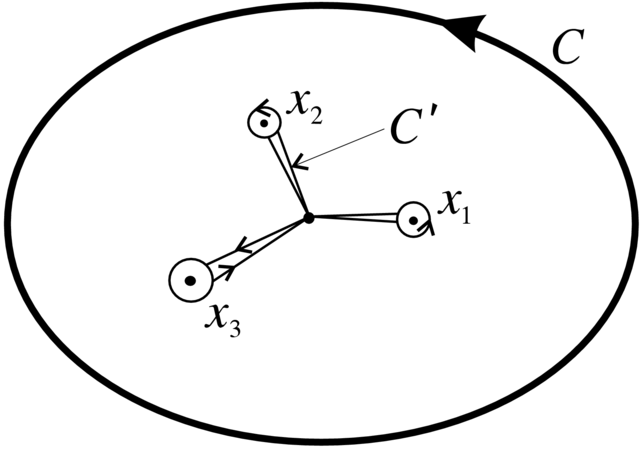
Możemy zdeformować krzywą do krzywej ![]() złożonej z układu pętli wokół punktów równowagi
złożonej z układu pętli wokół punktów równowagi ![]() i układu odcinków łączących te pętle z punktem bazowym.
Ponieważ obroty pola wzdłuż odcinków znoszą sie parami to
i układu odcinków łączących te pętle z punktem bazowym.
Ponieważ obroty pola wzdłuż odcinków znoszą sie parami to ![]() jest równe sumie obrotów pola wokół punktów
osobliwych (patrz Rysunek 2.11). ∎
jest równe sumie obrotów pola wokół punktów
osobliwych (patrz Rysunek 2.11). ∎
Lemat 2.25.Jeśli ![]() jest zamkniętą
przywą fazową pola
jest zamkniętą
przywą fazową pola ![]() to
to![]()
Dowód. Korzystając z własności niezmienniczości
indeksu względem deformacji (w klasie (2.12)) możemy zdeformować
krzywą i pole tak, aby otrzymać ![]() (z dodatnią lub ujemną orientacją) i pole
(z dodatnią lub ujemną orientacją) i pole ![]() będzie styczne
do tej krzywej. Łatwo widać, że kąt wektora
będzie styczne
do tej krzywej. Łatwo widać, że kąt wektora ![]() na
na ![]() jest `opóźniony' lub `przyspieszony' względem kątu punktu
jest `opóźniony' lub `przyspieszony' względem kątu punktu ![]() o
o ![]() ∎
∎
Następujący wniosek uściśla Twierdzenie 2.21.
Wniosek 2.26. Jeśli![]() jest zamkniętą krzywą fazową pola
jest zamkniętą krzywą fazową pola ![]() to
to
gdzie sumujemy po punktach równowagi pola wewnątrz obszaru
zakreślonego przez krzywą![]()
2.3. Kryterium Dulaca
Rozważmy pole wektorowe ![]()
![]() z zamkniętą krzywą fazową
z zamkniętą krzywą fazową ![]() , czyli trajektorią okresową
, czyli trajektorią okresową ![]() o okresie
o okresie ![]() Rozważmy cięcie
Rozważmy cięcie ![]() (prostopadłe do
(prostopadłe do ![]() w
w ![]() i odpowiednie przekształcenie powrotu Poincarégo
i odpowiednie przekształcenie powrotu Poincarégo ![]() Utożsamiając
Utożsamiając ![]() z
z ![]() mamy
mamy
Definicja 2.27. Liczba ![]() nazywa się wykładnikiem charakterystycznym orbity okresowej
nazywa się wykładnikiem charakterystycznym orbity okresowej ![]() (Zadanie
2.58).
(Zadanie
2.58).
Twierdzenie 2.28 (Dulac). Mamy
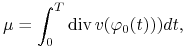 |
gdzie ![]() oznacza dywergencją pola
wektorowego
oznacza dywergencją pola
wektorowego ![]() (patrz wzór(6.29) poniżej).
(patrz wzór(6.29) poniżej).
Dowód. Rozważmy równanie w wariacjach względem
warunków początkowych wzdłuż rozwiązania ![]()
(patrz wzór (6.13)). Wybierzmy dwa warunki początkowe dla tego równania: ![]() jako jednostkowy wektor styczny do
jako jednostkowy wektor styczny do ![]() w
w ![]() i
i ![]() jako jednostkowy wektor prostopadły do
jako jednostkowy wektor prostopadły do ![]() w
w ![]() One odpowiadają dwóm typom zaburzenia warunku początkowego
One odpowiadają dwóm typom zaburzenia warunku początkowego ![]() dla równania
dla równania ![]()
![]() i
i ![]()
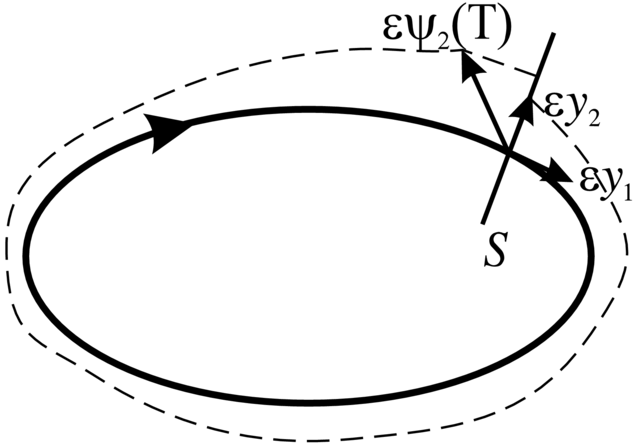
Zgodnie ze wzorem (6.28) rozwiązania ![]() i
i ![]() spełniające powyższe warunki początkowe rozpinają równoległoboki, których pole jest równe Wrońskianowi
spełniające powyższe warunki początkowe rozpinają równoległoboki, których pole jest równe Wrońskianowi ![]() tych rozwiązań. Dla
tych rozwiązań. Dla ![]() mamy
mamy ![]() bo
bo ![]() w istocie reprezentuje rozwiązanie
okresowe
w istocie reprezentuje rozwiązanie
okresowe ![]() z nieco przesuniętym punktem początkowym
(na
z nieco przesuniętym punktem początkowym
(na ![]() . Natomiast
. Natomiast ![]() jest pewnym wektorem zawiązanym
z wartością rozwiązania
jest pewnym wektorem zawiązanym
z wartością rozwiązania ![]() dla
dla ![]() które nie musi nawet trafić
w cięcie
które nie musi nawet trafić
w cięcie ![]() (patrz Rysunek 2.12). Ale rzut
(patrz Rysunek 2.12). Ale rzut ![]() wektora
wektora ![]() na
na ![]() ma naturalną interpretację
ma naturalną interpretację ![]() gdzie
gdzie ![]() jest przekształceniem powrotu.
jest przekształceniem powrotu.
Zauważmy teraz, że równoległobok rozpięty przez wektory ![]() i
i ![]() ma takie samo pole
ma takie samo pole ![]() jak długość rzutu wektora
jak długość rzutu wektora ![]() na
na ![]() To oznacza, że
To oznacza, że
Ale Twierdzenie 6.23, czyli ![]() z
z ![]() pozwala wyliczyć
pozwala wyliczyć ![]() Ponieważ
Ponieważ ![]() to mamy
to mamy ![]() ∎
∎
Twierdzenie Dulaca okazuje się być użyteczne przy pokazywaniu braku cykli granicznych dla pewnych pól wektorowych. Zilustrujemy to na następującum przykładzie.
Przykład 2.29 (Układ Jouanolou). Ma on następującą postać
Zgodnie z Twierdzeniem 2.21 każdy cykl graniczny tego pola powinien okrążać przynajmniej jeden punkt osobliwy. Równania punktów
osobliwych, czyli ![]() i
i ![]() prowadzą do
prowadzą do ![]() Zatem jest tylko jeden (rzeczywisty) punkt równowagi
Zatem jest tylko jeden (rzeczywisty) punkt równowagi ![]()
Część liniowa układu w tym punkcie zadaje się macierzą
z równaniem charakterystycznym ![]() Zatem punkt
Zatem punkt ![]() jest stabilnym ogniskiem.
jest stabilnym ogniskiem.
Przypuśćmy, że ![]() jest cyklem granicznym wokół
jest cyklem granicznym wokół ![]() i najbliższym dla tego punktu (wszystkie cykle
graniczne tworzą `gniazdo' wokół
i najbliższym dla tego punktu (wszystkie cykle
graniczne tworzą `gniazdo' wokół ![]() ). Łatwo widać,
że
). Łatwo widać,
że ![]() musi być niestabilny (przynajmniej od wewnątrz).
musi być niestabilny (przynajmniej od wewnątrz).
Z drugiej strony, dywergencja pola Jouanolou wynosi
Widać, że jeśli ![]() jest parzyste, to div
jest parzyste, to div![]() (dla
prawie wszystkich punktów krzywej fazowej) i Twierdzenie Dulaca
implikuje, że wykładnik charakterystyczny cyklu
(dla
prawie wszystkich punktów krzywej fazowej) i Twierdzenie Dulaca
implikuje, że wykładnik charakterystyczny cyklu ![]() jest ujemny
(sprzeczność z niestabilnością
jest ujemny
(sprzeczność z niestabilnością ![]()
Jeśli ![]() jest nieparzyste to ten argument również pracuje,
tylko trzeba najpierw pokazać, że
jest nieparzyste to ten argument również pracuje,
tylko trzeba najpierw pokazać, że ![]() musi leżeć w
pierwszej ćwiartce, patrz Rysunek 2.13 (Zadanie 2.59).
musi leżeć w
pierwszej ćwiartce, patrz Rysunek 2.13 (Zadanie 2.59).
Twierdzenie Dulaca ma jeszcze inne zastosowania.
Definicja 2.30. Funkcja ![]()
![]() nazywa się funkcją Dulaca
dla pola wektorowego
nazywa się funkcją Dulaca
dla pola wektorowego ![]() , jeśli
, jeśli ![]() ma
stały znak w obszarze
ma
stały znak w obszarze ![]()
Twierdzenie 2.31.Jeśli dla pola wektorowego ![]() istnieje funkcja Dulaca
istnieje funkcja Dulaca ![]() w obszarze
w obszarze ![]() to każdy cykl graniczny pola leżący w
to każdy cykl graniczny pola leżący w ![]() jest stabiln,y gdy
jest stabiln,y gdy ![]() (odpowiednio niestabilny, gdy
(odpowiednio niestabilny, gdy![]()
Dowód. Pomnożenie pola wektorowego przez funkcję dodatnią nie zmienia portretu fazowego tego pola. Zmienia się tylko prędkość punktu (tj. rozwiązania) wzdłuż krzywej fazowej. ∎
Uwaga 2.32. Można w Twierdzeniu 2.31 dopuścić nieostre
nierówności ![]() lub
lub ![]() Ale wtedy trzeba wykluczyć możliwość, że ewentualny cykl jest całkowicie
zawarty w krzywej
Ale wtedy trzeba wykluczyć możliwość, że ewentualny cykl jest całkowicie
zawarty w krzywej ![]()
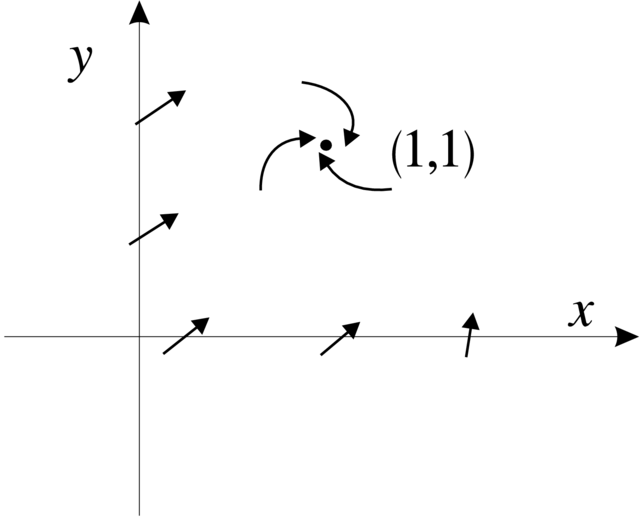
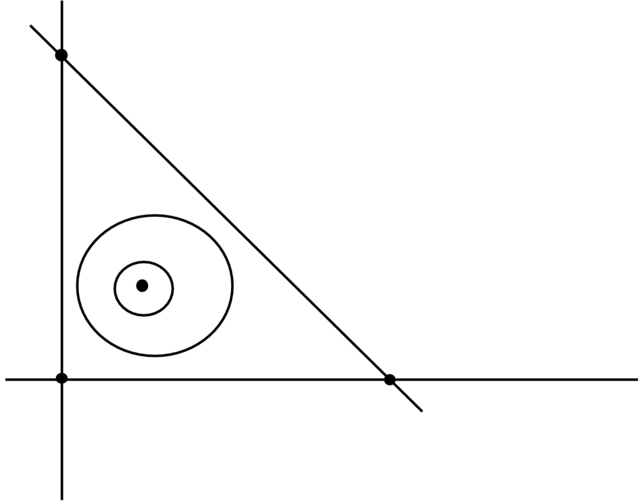
Przykład 2.33. (Uogólniony układ Lotki–Volterry). Jest to układ opisujący zmianę populacji drapieżników i ofiar (np. wilków i zajęcy)
(z ![]() ) w obszarze
) w obszarze ![]() Równania
Równania ![]() i
i ![]() definiują punkt osobliwy
definiują punkt osobliwy ![]() o
którym założymy, że leży w pierwszej ćwiartce i że
wyznacznik macierzy części liniowej w
o
którym założymy, że leży w pierwszej ćwiartce i że
wyznacznik macierzy części liniowej w ![]() jest dodatni (tylko wtedy indeks pola w
jest dodatni (tylko wtedy indeks pola w ![]() wynosi
wynosi
![]() i jest szansa na cykl graniczny). Twierdzę, że:
i jest szansa na cykl graniczny). Twierdzę, że:
jeśli ![]() to mamy centrum w
to mamy centrum w ![]() a jeśli
a jeśli ![]() to nie ma rozwiązań okresowych.
to nie ma rozwiązań okresowych.
Aby to potwierdzić, rozważmy następującą kandydatkę na funkcję Dulaca
Sprawdzamy (z ![]() ):
):
![\begin{array}[]{lll}\text{div}\left(\Phi v\right)&=&\frac{\partial}{\partial x}x^{{C/A}}\left[Ay-B(1-x-y)\right]y^{{B/D-1}}\cr&&+\frac{\partial}{\partial y}y^{{B/D}}\left[C(1-x-y)-Dx\right]x^{{C/A-1}}\cr&=&x^{{C/A-1}}y^{{B/D-1}}\left\{\frac{C}{A}\left[Ay-Bz\right]+Bx+\frac{B}{D}\left[Cz-Dx\right]-Cy\right\}\cr&=&\frac{BC}{AD}(A-D)x^{{C/A-1}}y^{{B/D-1}}z.\end{array}](wyklady/rrj/mi/mi869.png) |
Jeśli ![]() , to pole
, to pole ![]() jest hamiltonowskie i ma całkę
pierwszą (parz Rysunek 2.14).
jest hamiltonowskie i ma całkę
pierwszą (parz Rysunek 2.14).
Jeśli ![]() to
to ![]() jest funkcją Dulaca w obszarze
jest funkcją Dulaca w obszarze ![]() lub w obszarze
lub w obszarze ![]() . Ale tożsamość
. Ale tożsamość
(przy ![]() implikuje, że ewentualny cykl graniczny nie może
przechodzić przez odcinek
implikuje, że ewentualny cykl graniczny nie może
przechodzić przez odcinek ![]()
![]() Dalsze rozumowanie przebiega
tak samo jak w przykładzie z układem Jouanolou.
Dalsze rozumowanie przebiega
tak samo jak w przykładzie z układem Jouanolou.
Przykład 2.34 (Równanie van der Pola). Jest to następujący układ
szczególny przypadek układu Liénarda. Pojawia się on w
elektrotechnice, dla układu składającego się z kondensatora o
pojemności ![]() cewki o indukcyjności
cewki o indukcyjności ![]() i pewnego nieliniowego
elementu (typu diody) zastępującego opornik. W przypadku układu
i pewnego nieliniowego
elementu (typu diody) zastępującego opornik. W przypadku układu ![]() (cewka, kondensator, opornik) bilans różnic potencjałów
daje równanie
(cewka, kondensator, opornik) bilans różnic potencjałów
daje równanie ![]() na natężenie prądu
na natężenie prądu ![]() w obwodzie; w naszym przypadku człon
w obwodzie; w naszym przypadku człon ![]() jest zastępowany członem
jest zastępowany członem ![]() czyli
czyli
to jest właśnie oryginalne równanie van der Pola. Po
zamianie ![]() i podstawieniu
i podstawieniu ![]() i
i ![]() dostajemy powyższy układ van der Pola z
dostajemy powyższy układ van der Pola z ![]() . Po więcej szczegółów odsyłam do książki D. Arrowsmitha
and K. Place'a [6].
. Po więcej szczegółów odsyłam do książki D. Arrowsmitha
and K. Place'a [6].
Udowodnimy, że:
układ van der Pola posiada dokładnie jeden cykl graniczny.
Po pierwsze zauważmy, że ![]() jest jedynym punktem
osobliwym z macierzą części liniowej
jest jedynym punktem
osobliwym z macierzą części liniowej ![]() czyli, że
czyli, że ![]() i ten punkt jest
niestabilny (ognisko lub węzeł).
i ten punkt jest
niestabilny (ognisko lub węzeł).
Rozważmy funkcję
![\begin{array}[]{lll}f(x,y)&=&y^{{2}}+a(x^{{3}}/3-3)y+x^{{2}}-c\\
&=&\left[y+\frac{1}{2}a\left(\frac{x^{{3}}}{3}-x\right)\right]^{{2}}-g(x^{{2}})-c\\
&=&y_{{1}}^{{2}}-g(x^{{2}})-c,\end{array}](wyklady/rrj/mi/mi922.png) |
gdzie
a stała ![]() i jest dostatecznie mała. Interesuje nasz krzywa
i jest dostatecznie mała. Interesuje nasz krzywa ![]() która we współrzędnych
która we współrzędnych ![]() ma
postać
ma
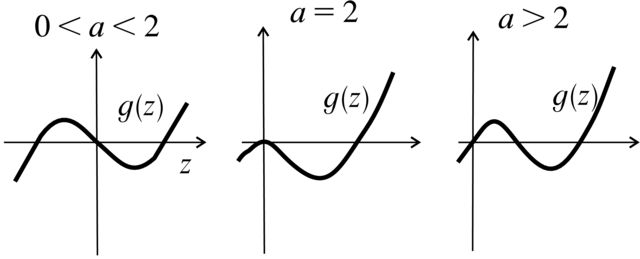
postać ![]() Z własności:
Z własności: ![]()
![]() dla
dla ![]()
![]() dla
dla ![]()
![]() i
i ![]() gdy
gdy ![]() możemy odtworzyć
wykres funkcji
możemy odtworzyć
wykres funkcji ![]() jest on przedstawiony na Rysunku 2.15. Stąd
wynika też kształt krzywej
jest on przedstawiony na Rysunku 2.15. Stąd
wynika też kształt krzywej ![]() na płaszczyźnie zmiennych
na płaszczyźnie zmiennych ![]() (przedstawiony na Rysunku 2.16). (Na płaszczyźnie zmiennych
(przedstawiony na Rysunku 2.16). (Na płaszczyźnie zmiennych ![]() ta krzywa jest w pewnym sensie `kopnięta'). Zauważmy, że
krzywa
ta krzywa jest w pewnym sensie `kopnięta'). Zauważmy, że
krzywa ![]() ma trzy składowe, z których jedna okrąża punkt
ma trzy składowe, z których jedna okrąża punkt ![]()
Okazuje się, że funkcja
jest funkcją Dulaca dla układu van der Pola w obszarze ![]()
Rzeczywiście, mamy
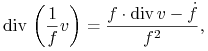 |
gdzie
i ![]() dla
dla ![]() (Zadanie 2.60).
(Zadanie 2.60).
Stąd otrzymujemy dwa wnioski:
(a) ![]() tzn. pole `wchodzi' do obszaru
tzn. pole `wchodzi' do obszaru ![]()
(b) W obszarze ![]() może być co najwyżej jeden cykl
graniczny, przy tym stabilny.
może być co najwyżej jeden cykl
graniczny, przy tym stabilny.
Pozostaje jeszcze udowodnić, że w obszarze ![]() istnieje jakiś
cykl graniczny. W tym celu skonstruujemy pierścień
istnieje jakiś
cykl graniczny. W tym celu skonstruujemy pierścień ![]() spełniający założenia Twierdzenia Poincarégo–Bendixsona. Wewnętrzny brzeg tego pierścienia to mała zamknięta składowa
krzywej
spełniający założenia Twierdzenia Poincarégo–Bendixsona. Wewnętrzny brzeg tego pierścienia to mała zamknięta składowa
krzywej ![]() wokół
wokół ![]() Brzeg zewnętrzny będzie składać się z kawałków nieograniczonych składowych
krzywej
Brzeg zewnętrzny będzie składać się z kawałków nieograniczonych składowych
krzywej ![]() i z `poprawionych' łuków okręgu
i z `poprawionych' łuków okręgu ![]() dla dużego promienia
dla dużego promienia ![]()
Z własności (a) wynika, że na kawałkach brzegu w ![]() pole
wchodzi do
pole
wchodzi do ![]() . Dalej, z
. Dalej, z
wynika, że ![]() poza pasem
poza pasem ![]() Ale w tym pasie mamy
Ale w tym pasie mamy
czyli przyrost ![]() (a tym samym i przyrost
(a tym samym i przyrost ![]() jest ograniczony przez stałą niezależną od
jest ograniczony przez stałą niezależną od ![]() Teraz już łatwo poprawić
odpowiednie kawałki zewnętrznego brzegu pierścienia
Teraz już łatwo poprawić
odpowiednie kawałki zewnętrznego brzegu pierścienia ![]() , aby tam też pole wchodziło do
, aby tam też pole wchodziło do ![]() (patrz Przykład 2.20).
(patrz Przykład 2.20).
Powyższy dowód jednoznaczności cyklu granicznego pochodzi od L.
Czerkasa z Mińska Białoruskiego. W Zadaniu 4.17 poniżej
proponujemy inny dowód jednoznaczności cyklu granicznego w
przypadku, gdy parametr ![]() jest mały.
jest mały.
2.4. Rysowanie portretów fazowych na płaszczyźnie
Jak już było powiedziane w Definicji 2.1 portret fazowy pola
wektorowego ![]() na płaszczyźnie to rozbicie płaszczyzny
na płaszczyźnie to rozbicie płaszczyzny ![]() na krzywe fazowe tego pola. Elementami portretu
fazowego są: punkty osobliwe, zamknięte krzywe fazowe, separatrysy
punktów osobliwych i zachowanie na nieskończoności. Pokrótce
je kolejno omówimy.
na krzywe fazowe tego pola. Elementami portretu
fazowego są: punkty osobliwe, zamknięte krzywe fazowe, separatrysy
punktów osobliwych i zachowanie na nieskończoności. Pokrótce
je kolejno omówimy.
2.4.1. Punkty osobliwe
Dzielą się one na elementarne i nieelementarne.Przy tym elementarne punkty osobliwe można podzielić na niezdegenerowane i zdegenerowane.
Definicja 2.35. Punkt równowagi ![]() pola wektorowego
pola wektorowego ![]()
![]() , nazywa się niezdegenerowanym jeśli
, nazywa się niezdegenerowanym jeśli ![]()
Punkt równowagi ![]() płaskiego pola wektorowego
płaskiego pola wektorowego ![]()
![]() nazywa się elementarnym jeśli
przynajmniej jedna wartość własna macierzy
nazywa się elementarnym jeśli
przynajmniej jedna wartość własna macierzy ![]() jest niezerowa. W ostatnim przypadku punkt
jest niezerowa. W ostatnim przypadku punkt ![]() jest:
jest:
siodłem, jeśli ![]() dla
wartości własnych
dla
wartości własnych ![]() amacierzy
amacierzy ![]()
węzłem stabilnym (odpowiednio węzłem
niestabilnym), jeśli![]() (odpowiednio
(odpowiednio ![]()
ogniskiem stabilnym (odpowiednio ogniskiem
niestabilnym), jeśli ![]() i
i ![]() (odpowiednio
(odpowiednio ![]()
siodło–węzłem, jeśli ![]()
![]()
Lokalne portrety fazowe w otoczeniu elementarnych punktów osobliwych zdefiniowanych powyżej są przedstawione na Rysunkach 2.17 i 2.18.
Uwaga 2.36. W przypadku ![]() czyli czysto urojonych wartości własnych punkt krytyczny
czyli czysto urojonych wartości własnych punkt krytyczny ![]() może być ogniskiem stabilnym lub niestabilnym (dokładniej, słabym ogniskiem) lub centrum; patrz Stwierdzenie 2.11
powyżej.
może być ogniskiem stabilnym lub niestabilnym (dokładniej, słabym ogniskiem) lub centrum; patrz Stwierdzenie 2.11
powyżej.
Uwaga 2.37. Pojęcie siodła–węzła podane powyżej jest dosyć szerokie. Rzecz w tym, że możemy mieć następujące modelowe sytuacje
| (2.13) | |||||
| (2.14) |
W Podrozdziale 3.3 poniżej wzory (2.13)–(2.14) będą dokładniej uzasadnione. Gdy ![]() i
i ![]() to siodło–węzeł jest w pewnym sensie zdegenerowane; mówimy, że ma kowymiar
to siodło–węzeł jest w pewnym sensie zdegenerowane; mówimy, że ma kowymiar
![]()
Z punktu widzenia topologicznego lokalny portret fazowy nie zależy od ![]() Te portrety są przedstawione na Rysunku 2.18.
Te portrety są przedstawione na Rysunku 2.18.
Uwaga 2.38 (Nieelementarne punkty osobliwe). Przypomnę, że
tutaj mamy ![]() Niestety nie istnieje zadowalająca klasyfikacja takich osobliwości. Ale istnieje pewna skuteczna
metoda ich badania. Jest to metoda rozdmuchiwania osobliwości
(albo rozwiązywania osobliwości).
Niestety nie istnieje zadowalająca klasyfikacja takich osobliwości. Ale istnieje pewna skuteczna
metoda ich badania. Jest to metoda rozdmuchiwania osobliwości
(albo rozwiązywania osobliwości).
Polega ona na prostej operacji wprowadzenia biegunowych współrzędnych ![]() na płaszczyźnie. Zatem jeśli
mamy, na przykład,
na płaszczyźnie. Zatem jeśli
mamy, na przykład,
| (2.15) |
to w zmiennych biegunowych dostajemy
| (2.16) |
gdzie
Zauważmy, że prawe strony równań (2.16) zerują się
przy ![]() Podzielmy te prawe strony przez
Podzielmy te prawe strony przez ![]() w obszarze
w obszarze ![]() portret
fazowy nie zmieni się, jedynie `prędkość' punktu wzdłuż
krzywej fazowej będzie inna,ale niezerowa. (Mogłoby się zdarzyć, że
portret
fazowy nie zmieni się, jedynie `prędkość' punktu wzdłuż
krzywej fazowej będzie inna,ale niezerowa. (Mogłoby się zdarzyć, że ![]() ale wtedy dzielimy przez
ale wtedy dzielimy przez ![]() Jest
to tzw. orbitalna równoważność, o której opowiadamy poniżej.
Jest
to tzw. orbitalna równoważność, o której opowiadamy poniżej.
Ale po takiej operacji dostajemy pole wektorowe na cylindrze ![]() (z którego dla nas jest istotna część
(z którego dla nas jest istotna część ![]() przy tym z izolowanymi punktami osobliwymi na okręgu
przy tym z izolowanymi punktami osobliwymi na okręgu ![]() Jeśli
wspólczynniki
Jeśli
wspólczynniki ![]() są typowe, to te punkty osobliwe są
już niezdegenerowane, czyli elementarne.
są typowe, to te punkty osobliwe są
już niezdegenerowane, czyli elementarne.
W przeciwnym przypadku powtarzamy procedurę rozdmuchania (połączo-
ną z dzieleniem) w otoczeniu każdego nieelementarnego punktu
osobliwego ![]()
![]() (z nowymi wspólrzędnymi
(z nowymi wspólrzędnymi ![]()
![]() Okazuje się, że jeśli wyjściowe pole wektorowe, jak (2.15), jest analityczne, to po skończonej liczbie takich operacji rozdmuchania dostajemy pole wektorowe na
pewnej powierzchnii
Okazuje się, że jeśli wyjściowe pole wektorowe, jak (2.15), jest analityczne, to po skończonej liczbie takich operacji rozdmuchania dostajemy pole wektorowe na
pewnej powierzchnii ![]() z elementarnymi punktami osobliwymi. (Jest to
trudne twierdzenie, po którego dowód odsyłam do mojej książki “The monodromy group” [20].)
z elementarnymi punktami osobliwymi. (Jest to
trudne twierdzenie, po którego dowód odsyłam do mojej książki “The monodromy group” [20].)
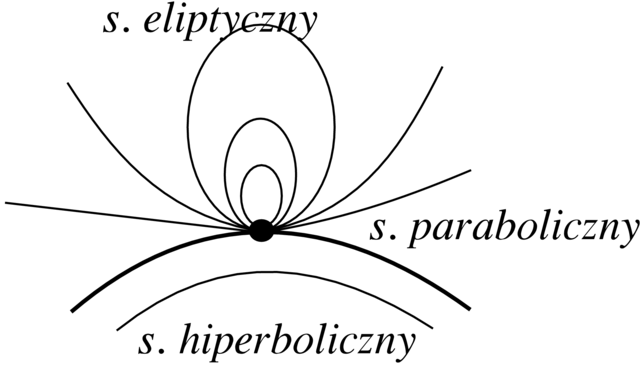
W przypadku nieelementarnego punktu osobliwego często jego otoczenie można podzielić na sektory: hiperboliczne, paraboliczne, i eliptyczne. Są one zobrazowane na Rysunku 2.19. Jest pewna teoria związana z nimi, którą nie będziemy się zajmować. Zainteresowanych słuchaczy odsyłam do książki P. Hartmana [13].
2.4.2. Zamknięte krzywe fazowe
One odpowiadają rozwiązaniom (i trajektoriom) okresowym i były dosyć szczegółowo omawiane w poprzednim podrozdziale.
2.4.3. Separatrysy punktów osobliwych
Definicja 2.39.Separatrysą punktu osobliwego ![]() pola wektorowego
pola wektorowego ![]() nazywamy krzywą fazową tego pola która
`dąży' do
nazywamy krzywą fazową tego pola która
`dąży' do ![]() pod określonym granicznym kierunkiem i jest
`wyróżniona' wśród takich krzywych.
pod określonym granicznym kierunkiem i jest
`wyróżniona' wśród takich krzywych.
Na przykład, dla siodła separatrysami są składowe `nakłutych'
rozmaitości stabilnej ![]() i niestabilnej
i niestabilnej ![]() w sumie mamy cztery separatrysy.
w sumie mamy cztery separatrysy.
W ogólnym przypadku, gdy mamy podział na sektory hiperboliczne, eliptyczne i paraboliczne, separatrysy występują na brzegach sektorów hiperbolicznych.
Uwaga 2.40. Ważnym elementem portretu fazowego pola wektorowego
jest `los' drugiego końca danej separatrysy ![]() .
.
Może on lądować w innym punkcie osobliwym ![]() , zwykle w jego
sektorze parabolicznym. Ale może też nawijać się na ognisko.
Szczególny jest przypadek, gdy
, zwykle w jego
sektorze parabolicznym. Ale może też nawijać się na ognisko.
Szczególny jest przypadek, gdy ![]() jest separatrysą zarówno dla
jest separatrysą zarówno dla
![]() jak i dla
jak i dla ![]() mamy wtedy do czynienia z tzw. połączeniem separatrys.
mamy wtedy do czynienia z tzw. połączeniem separatrys.
Drugi koniec separatrysy może też nawijać się na cykl graniczny.
2.4.4. Zachowanie na nieskończoności
Istnieje wiele uzwarceń płaszczyzny ![]() Jednym z nich
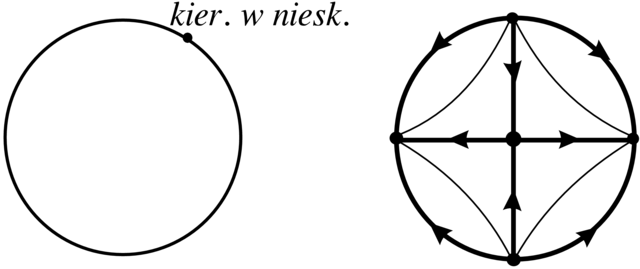
jest tzw. uzwarcenie Poincarégo (albo płaszczyzna Poincarégo). Polega ono na uzupełnieniu płaszczyzny okręgiem przez dodanie
wszystkich `kierunków w nieskończoności'. Płaszczyzna Poincarégo jest dyfeomorficzna z dyskiem:
Jednym z nich
jest tzw. uzwarcenie Poincarégo (albo płaszczyzna Poincarégo). Polega ono na uzupełnieniu płaszczyzny okręgiem przez dodanie
wszystkich `kierunków w nieskończoności'. Płaszczyzna Poincarégo jest dyfeomorficzna z dyskiem: ![]() (patrz Rysunek 2.20).10W matematyce bardziej rozpowszechnione jest uzwarcenie za pomocą płaszczyzny rzutowej
(patrz Rysunek 2.20).10W matematyce bardziej rozpowszechnione jest uzwarcenie za pomocą płaszczyzny rzutowej ![]() Różnica pomiędzy
uzwarceniem Poincarégo polega na tym, że w płaszczyźnie
rzutowej dwa antypodyczne kierunki w nieskończoności są utożsamiane. Niestety, płaszczyzna rzutowa jest rozmaitością
nieorientowalną i nie da się jej narysować (w przeciwieństwie do płaszczyzny Poincarégo).
Różnica pomiędzy
uzwarceniem Poincarégo polega na tym, że w płaszczyźnie
rzutowej dwa antypodyczne kierunki w nieskończoności są utożsamiane. Niestety, płaszczyzna rzutowa jest rozmaitością
nieorientowalną i nie da się jej narysować (w przeciwieństwie do płaszczyzny Poincarégo).
Uzwarcenie Poincarégo jest przydatne przy badaniu zachowania się
krzywych fazowych wielomianowych pól wektorowych, tzn. takich układów ![]()
![]() , których prawe strony
, których prawe strony ![]() i
i ![]() są wielomianami.
są wielomianami.
Wtedy w otoczeniu okręgu w nieskończoności można wpropwadzić współrzędne typu biegunowego
Dostaniemy układ postaci
czyli z biegunem w zbiorze ![]() (okrąg w nieskończoności). Mnożąc prawe strony przez
(okrąg w nieskończoności). Mnożąc prawe strony przez ![]() , co prowadzi do orbitalnej równoważności w obszarze
, co prowadzi do orbitalnej równoważności w obszarze ![]() dostajemy porządne pole wektorowe w otoczeniu okręgu w nieskończoności.
dostajemy porządne pole wektorowe w otoczeniu okręgu w nieskończoności.
Zauważmy, że punkty osobliwe ![]()
![]() nowego
pola odpowiadają sytuacji gdy jakaś krzywa fazowa układu
nowego
pola odpowiadają sytuacji gdy jakaś krzywa fazowa układu ![]()
![]() dąży do nieskończoności (przy
dąży do nieskończoności (przy ![]() lub przy
lub przy ![]() pod granicznym
kierunkiem
pod granicznym
kierunkiem ![]()
Przykład 2.41. Liniowe pole wektorowe ![]()
![]() prowadzi do portretu fazowego w płaszczyźnie Poincarégo
przedstawionego na Rysunku 2.20.
prowadzi do portretu fazowego w płaszczyźnie Poincarégo
przedstawionego na Rysunku 2.20.
2.4.5. Orbitalna równoważność
Definicja 2.42. Dwa pola wektorowe ![]() na
na ![]() i
i ![]() na
na ![]() są orbitalnie równoważne, jeśli mają takie same
portrety fazowe z topologicznego punktu widzenia. To znaczy, istnieje
homeomorfizm
są orbitalnie równoważne, jeśli mają takie same
portrety fazowe z topologicznego punktu widzenia. To znaczy, istnieje
homeomorfizm ![]() taki, że
taki, że ![]() krzywa fazowa
krzywa fazowa ![]() krzywa
fazowa
krzywa
fazowa ![]()
Pole wektorowe ![]() na
na ![]() jest orbitalnie strukturalnie stabilne, jeśli każde pole
jest orbitalnie strukturalnie stabilne, jeśli każde pole ![]() na
na ![]() dostatecznie bliskie polu
dostatecznie bliskie polu ![]() (w odpowiedniej topologii) jest orbitalnie równoważne z polem
(w odpowiedniej topologii) jest orbitalnie równoważne z polem ![]()
Jak łatwo się przekonać, powyższa definicja orbitalnej równoważności i orbitalnej strukturalnej stabilności jest słabsza od definicji równoważności i strukturalnej stabilności podanej w Definicji 1.24.
Zatem z Twierdzenie Grobmana–Hartmana (Twierdzenie 1.23) i następującego po nim Stwierdzenia 1.25 wynika, że dwa pola wektorowe w otoczeniu hiperbolicznych punktów osobliwych o takich samych wymiarach rozmaitości stabilnej i niestabilnej są orbitalnie równoważne. Są one też orbitalnie strukturalnie stabilne.
Poniżej, bez dowodu podajemy warunki konieczne dla orbitalnej strukturalnej stabilności pola wektorowego na płaszczyźnie.
Twierdzenie 2.43.Jeśli pole ![]() w obszarze
w obszarze![]() jest orbitalnie strukturalnie stabilne,
to:
jest orbitalnie strukturalnie stabilne,
to:
(i) jego punkty osobliwe są hiperboliczne,
(ii) jego zamknięte krzywe fazowe są hiperbolicznymi cyklami granicznymi,
(ii) nie ma połączeń separatrys.
Jeśli obszar ![]() jest zwarty (np. płaszczyzna Poincarégo), to powyższe warunki na orbitalną strukturalną stabilność są również dostateczne.
jest zwarty (np. płaszczyzna Poincarégo), to powyższe warunki na orbitalną strukturalną stabilność są również dostateczne.
ZADANIA
Zadanie 2.44. Wyliczyć rozwiązanie układu ![]()
![]() (wahadło matematyczne) z warunkiem początkowym
(wahadło matematyczne) z warunkiem początkowym ![]()
![]() odpowiadającemu
odpowiadającemu ![]()
Zadanie 2.45. Analogicznie jak w przypadku wahaddła matematycznego znaleźć całkę pierwszą i naszkicować krzywe fazowe dla układu Duffinga
Wyliczyć rozwiązanie z warunkiem początkowym ![]()
![]() .
.
Zadanie 2.46. Wyliczyć ![]() i
i ![]() w Przykładzie 2.4.
w Przykładzie 2.4.
Zadanie 2.47. Pokazać, że wartości własne macierzy ![]() w przekształceniu powrotu Poincarégo
w przekształceniu powrotu Poincarégo ![]() nie zależą od wyboru cięcia
nie zależą od wyboru cięcia ![]() do orbity okresowej
do orbity okresowej ![]()
Zadanie 2.48. Udowodnić wzór (2.4).
Zadanie 2.49. Wyliczyć współczynnik ![]() we wzorze
(2.6).
we wzorze
(2.6).
Zadanie 2.50. Przy założeniu, że po prawej stronie równania (2.7) występują tylko wyrazy kwadratowe (tj. ![]() i że
i że ![]() wyliczyć
wyliczyć ![]()
Zadanie 2.51. Pokazać, że dla liniowego pola wektorowego
liczba cykli granicznych wynosi ![]()
Zadanie 2.52. Pokazać, że zbiór ![]() graniczny
graniczny ![]() dla potoku
dla potoku ![]() jest domknięty i
niezmienniczy, tzn.
jest domknięty i
niezmienniczy, tzn. ![]() .
.
Zadanie 2.53. Pokazać, że w dowodzie Twierdzenia 2.19
kolejne punkty ![]() przecięcia trajektorii
przecięcia trajektorii ![]() punktu
punktu ![]() z
cięciem
z
cięciem ![]() układają się w ciąg monotoniczny, jak na
Rysunku 2.7.
układają się w ciąg monotoniczny, jak na
Rysunku 2.7.
Zadanie 2.54. Pokazać, że pole wektorowe (2.11) ma własność, że kwadrat promienia ![]() rośnie wzdluż rozwiązań dla małych
rośnie wzdluż rozwiązań dla małych ![]()
Zadanie 2.55. Policzyć indeks w ![]() dla następujących pól:
dla następujących pól:
Zadanie 2.56. Pokazać, że ![]() dla
kiełka pola
dla
kiełka pola ![]() w
w ![]() takiego, że
takiego, że ![]() Uwaga: przypadek
Uwaga: przypadek ![]() to zadanie z gwiazdką.
to zadanie z gwiazdką.
Zadanie 2.57. Pokazać, że pole wektorowe ![]()
![]() nie posiada cykli granicznych.
nie posiada cykli granicznych.
Zadanie 2.58. Pokazać, że wykładnik charakterystyczny orbity okresowej zdefiniowany w Definicji 2.27 jest dobrze określony.
Zadanie 2.59. Uzupełnić analizę układu Jouanolou w
przypadku nieparzystego ![]()
Zadanie 2.60. Wyliczyć div![]() w analizie układu van der Pola.
w analizie układu van der Pola.
Zadanie 2.61. Naszkicować portret fazowy (w ![]() dla układu
dla układu ![]()
![]()
Zadanie 2.62. Naszkicować portret fazowy dla układu ![]()
![]()
Zadanie 2.63. Naszkicować portret fazowy dla równań ![]() i
i ![]() gdzie
gdzie ![]()
Zadanie 2.64. Rozważmy pole wektorowe ![]() postaci (1.2),
czyli
postaci (1.2),
czyli ![]()
![]() chcemy
pokazać, że portret fazowy tego układu jest jak na Rysunku 1.2.
chcemy
pokazać, że portret fazowy tego układu jest jak na Rysunku 1.2.
(a) Zacznijmy od prostszego pola wektorowego ![]() zadanego układem
zadanego układem
| (2.17) |
Robiąc podstawienie ![]() naszkicować jego portret fazowy i
pokazać, że w otoczeniu
naszkicować jego portret fazowy i
pokazać, że w otoczeniu ![]() jest on jakościowo taki jak na
Rysunku 1.2 (tylko, że ma większy sektor eliptyczny). Pokazać też, że parabola
jest on jakościowo taki jak na
Rysunku 1.2 (tylko, że ma większy sektor eliptyczny). Pokazać też, że parabola ![]() jest niezmiennicza dla pola (2.17) i
zawiera separatrysy na granicy sektora hiperbolicznego.
jest niezmiennicza dla pola (2.17) i
zawiera separatrysy na granicy sektora hiperbolicznego.
(b) Stosując dwukrotnie rozdmuchanie pokazać, że pola ![]() i
i ![]() mają jakościowo takie same portrety fazowe w otoczeniu
mają jakościowo takie same portrety fazowe w otoczeniu ![]()
(c) Pokazać, że dodanie składnika ![]() do pola
do pola ![]() powo-
duje, że w obszarze
powo-
duje, że w obszarze ![]() (czyli cały
sektor eliptycznym dla
(czyli cały
sektor eliptycznym dla ![]() z brzegiem) przecinamy krzywe fazowe pola
z brzegiem) przecinamy krzywe fazowe pola ![]() pod kątem i tak, że krzywe fazowe pola
pod kątem i tak, że krzywe fazowe pola ![]() kierują się
bardziej w kierunku środka układu wspólrzędnych. Wywnioskować stąd, że wszystkie punkty z obszaru
kierują się
bardziej w kierunku środka układu wspólrzędnych. Wywnioskować stąd, że wszystkie punkty z obszaru ![]() dążą do
dążą do ![]() pod wpływem potoku fazowego
pod wpływem potoku fazowego ![]() .
.
(d) Pokazać, że również pozostałe punkty z
otoczenia ![]() albo leżą w stabilnej separatrysie
punktu
albo leżą w stabilnej separatrysie
punktu ![]() (tj. dla
(tj. dla ![]() albo wchodzą do obszaru
albo wchodzą do obszaru ![]() po
skończonym czasie pod wpływem potoku
po
skończonym czasie pod wpływem potoku ![]()