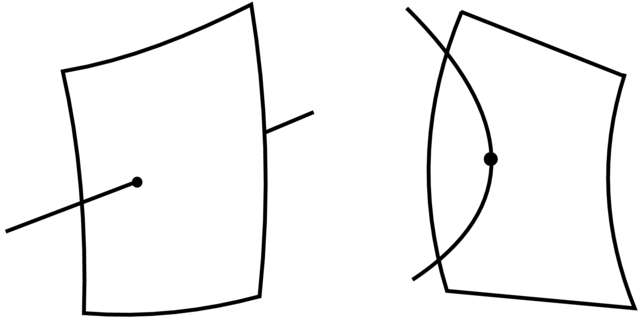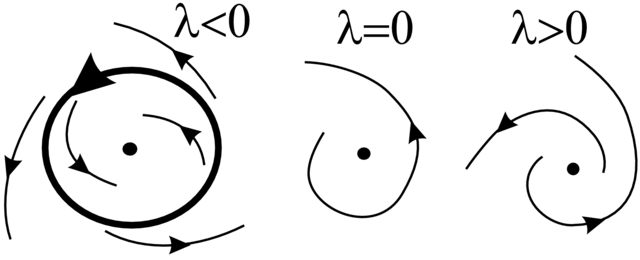Zagadnienia
3. Teoria bifurkacji
3.1. Wersalność
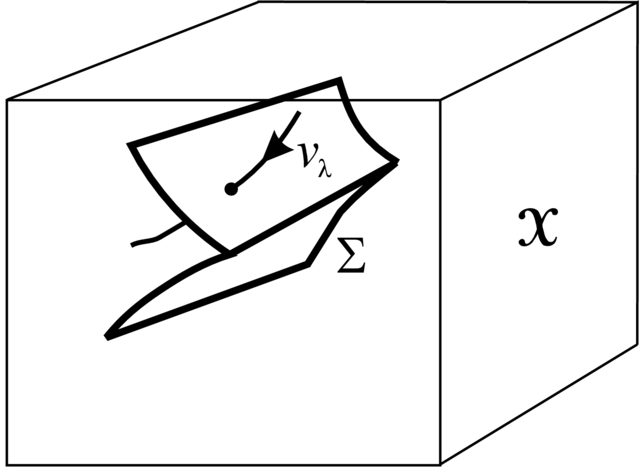
Zgodnie z Twierdzeniem 2.43 typowe pola wektorowe na zwartej ![]() wymia-
rowej rozmaitości
wymia-
rowej rozmaitości ![]() są orbitalnie strukturalnie stabilne. Jeśli oznaczymy przez
są orbitalnie strukturalnie stabilne. Jeśli oznaczymy przez ![]() nieskończenie wymiarową przestrzeń wszystkich pól wektorowych na
nieskończenie wymiarową przestrzeń wszystkich pól wektorowych na ![]() (danej klasy i z odpowiednią
topologią, o której nie będziemy mówić), to podzbiór
(danej klasy i z odpowiednią
topologią, o której nie będziemy mówić), to podzbiór
![]() , nazywany zbiorem bifurkacyjnym, przestrzeni
, nazywany zbiorem bifurkacyjnym, przestrzeni ![]() złożony z pól, które nie są orbtalnie strukturalnie
stabilne, powinien mieć kowymiar
złożony z pól, które nie są orbtalnie strukturalnie
stabilne, powinien mieć kowymiar ![]() Należy się spodziewać, że ten podzbiór
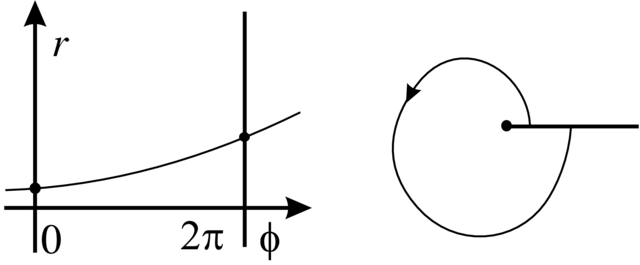
Należy się spodziewać, że ten podzbiór ![]() jest na ogół gładki, ale może mieć punkty nieregularne (jak na Rysunku 3.1). Te ostatnie punkty
powinny odpowiadać polom wektorowym, które mają osobliwości
bardziej skomplikowane niż pola odpowiadające typowym punktom z
jest na ogół gładki, ale może mieć punkty nieregularne (jak na Rysunku 3.1). Te ostatnie punkty
powinny odpowiadać polom wektorowym, które mają osobliwości
bardziej skomplikowane niż pola odpowiadające typowym punktom z ![]()
Jeśli wybierzemy przypadkowo pojedyncze pole z ![]() , to z
prawdopodobieństwem 1 będzie ono poza zbiorem
, to z
prawdopodobieństwem 1 będzie ono poza zbiorem ![]() Ale cała rodzina
Ale cała rodzina ![]() pól
wektorowych stanowi krzywą w
pól
wektorowych stanowi krzywą w ![]() i już może przeciąć hiperpowierzchnię
i już może przeciąć hiperpowierzchnię ![]() Spodziewamy się też,
że dla typowej rodziny odpowiednia krzywa przetnie hiperpowierzchnię
Spodziewamy się też,
że dla typowej rodziny odpowiednia krzywa przetnie hiperpowierzchnię
![]() pod kątem i w punktach typowych tej hiperpowierzchnii (patrz
Rysunek 3.1).
pod kątem i w punktach typowych tej hiperpowierzchnii (patrz
Rysunek 3.1).
Teoria bifurkacji zajmuje się badaniem zarówno geometrii zbioru
bifurkacyjnego ![]() jak i zachownia się wieloparametrowych rodzin pól wektorowych. My ograniczymy się do
jak i zachownia się wieloparametrowych rodzin pól wektorowych. My ograniczymy się do ![]() parametrowych rodzin.
parametrowych rodzin.
Należy zwrócić uwagę na jeszcze jeden aspekt tej sytuacji.
Na przestrzeni ![]() działa grupa
działa grupa ![]() orbitalnych równoważności i podzbiór bifurkacyjny
orbitalnych równoważności i podzbiór bifurkacyjny ![]() jest niezmienniczy
względem tego działania. Należy zatem powiązać analizę
jest niezmienniczy
względem tego działania. Należy zatem powiązać analizę
![]() parametrowych rodzin
parametrowych rodzin ![]() z działaniem
grupy
z działaniem
grupy ![]() V. Arnold w [5] wprowadził raz na zawsze porządek na tym
polu i poniższe definicje pochodzą od niego. My podajemy te
definicje dla
V. Arnold w [5] wprowadził raz na zawsze porządek na tym
polu i poniższe definicje pochodzą od niego. My podajemy te
definicje dla ![]() parametrowych rodzin, ale łatwo je uogólnić na
przypadek wieloparametrowy.11Ta filozofia pracuje również w innych ogólnych sytuacjach. Na
przykład, gdy
parametrowych rodzin, ale łatwo je uogólnić na
przypadek wieloparametrowy.11Ta filozofia pracuje również w innych ogólnych sytuacjach. Na
przykład, gdy ![]() jest przestrzenią funkcji
jest przestrzenią funkcji ![]() na rozmaitości a
na rozmaitości a ![]() jest grupą dyfeomorfizmów
jest grupą dyfeomorfizmów ![]() rozmaitości z działaniem
rozmaitości z działaniem ![]() Podobnie
Podobnie ![]() może być przestrzenią dyfeomorfizmów
może być przestrzenią dyfeomorfizmów ![]() rozmaitości
rozmaitości ![]() a grupa
a grupa ![]() dyfeomorfizmów
dyfeomorfizmów ![]() może działać poprzez sprzężenie:
może działać poprzez sprzężenie: ![]() .
.
Definicja 3.1. Dwie rodziny ![]() i
i ![]() ,
, ![]() , pól wektorowych na
, pól wektorowych na ![]() są orbitalnie równoważne, jeśli dla każdego
są orbitalnie równoważne, jeśli dla każdego ![]() pola
pola ![]() i
i ![]() są orbitalnie równoważne za pomocą
homeomorfizmu
są orbitalnie równoważne za pomocą
homeomorfizmu ![]() który zależy w sposób ciągły od parametru
który zależy w sposób ciągły od parametru ![]()
Mówimy, że rodzina ![]() jest
indukowana z rodziny
jest
indukowana z rodziny ![]() , jeśli istnieje ciągłe od wzorowanie
, jeśli istnieje ciągłe od wzorowanie ![]() takie, że
takie, że
Rodzina ![]() z zadanym polem
z zadanym polem ![]() , jest wersalna, jeśli
dowolna inna rodzina
, jest wersalna, jeśli
dowolna inna rodzina ![]() z
z ![]() jest orbitalnie równoważna rodzinie
indukowanej z rodziny
jest orbitalnie równoważna rodzinie
indukowanej z rodziny ![]()
Przykład 3.2. Rodzina ![]() jest indukowana z
rodziny
jest indukowana z
rodziny ![]() przy pomocy zamiany zmiennych
przy pomocy zamiany zmiennych ![]()
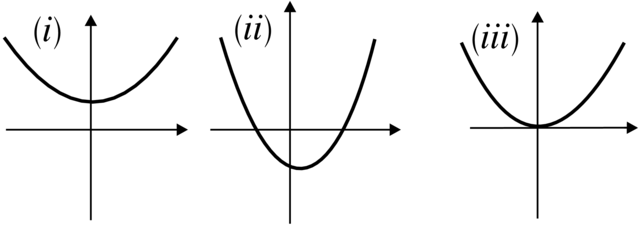
Przykład 3.3. Weźmy modelową rodzinę pól wektorowych
| (3.1) |
Odpowiednie portrety fazowe są przedstawione na Rysunku 3.2.
Weźmy teraz dowolną rodzinę postaci
| (3.2) |
gdzie ![]() jest gładką funkcją w otoczeniu
jest gładką funkcją w otoczeniu ![]() . Twierdzę, że
. Twierdzę, że
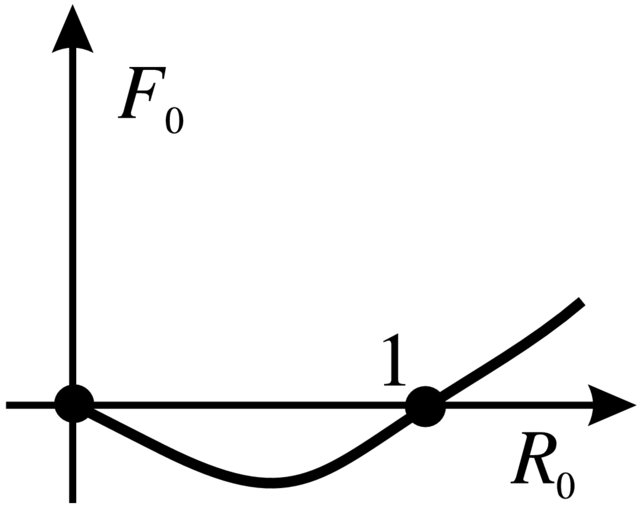
dla dażdego ![]() pole wektorowe
pole wektorowe ![]() posiada albo 1 albo 2 albo 0 punktów osobliwych w otoczeniu
posiada albo 1 albo 2 albo 0 punktów osobliwych w otoczeniu![]() Aby to zobaczyć rozważmy równanie
Aby to zobaczyć rozważmy równanie
gdzie ![]() Ponieważ
Ponieważ ![]() to
to ![]() i z Twierdzenia o
Funkcji Uwikłanej wynika istnienie gładkiej funkcji
i z Twierdzenia o
Funkcji Uwikłanej wynika istnienie gładkiej funkcji ![]() takiej, że jest spełnione równanie
takiej, że jest spełnione równanie ![]() To oznacza, że punkt
To oznacza, że punkt
jest punktem lokalnego minimum funkcji
![]()
![]() Mamy trzy możliwości na wartość pola
Mamy trzy możliwości na wartość pola ![]() w punkcie
w punkcie ![]() (i)
(i) ![]() (ii)
(ii) ![]() (iii)
(iii) ![]() W przypadku (i) pole
W przypadku (i) pole ![]() ma dokłanie jeden punkt równowagi (typu siodło–węzeł), w przypadku (ii) pole
ma dokłanie jeden punkt równowagi (typu siodło–węzeł), w przypadku (ii) pole ![]() ma dwa hiperboliczne punkty równowagi a w przypadku (iii) nie ma żadnych punktów równowagi (patrz Rysunek 3.3).
ma dwa hiperboliczne punkty równowagi a w przypadku (iii) nie ma żadnych punktów równowagi (patrz Rysunek 3.3).
Zatem dla każdego ![]() portret fazowy pola
portret fazowy pola ![]() jest
topologicznie równoważny z portretem fazowym pola
jest
topologicznie równoważny z portretem fazowym pola ![]() dla odpowiedniego
dla odpowiedniego ![]() Pojawia się naturalne pytanie, czy można tak dobrać
Pojawia się naturalne pytanie, czy można tak dobrać ![]() i homeomorfizmy
i homeomorfizmy ![]() realizujące orbitalne sprzężenie
realizujące orbitalne sprzężenie ![]() z
z ![]() aby zależność od
aby zależność od ![]() była ciągła. Okazuje się, że tak; to oznacza, że rodzina (3.1) jest wersalna.
była ciągła. Okazuje się, że tak; to oznacza, że rodzina (3.1) jest wersalna.
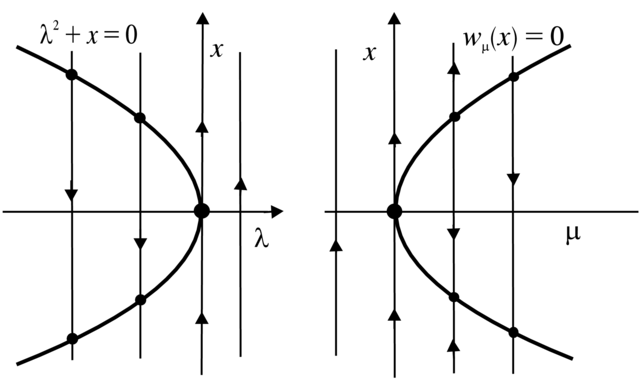
Aby się o tym przekonać, rozważmy najpierw przypadek, gdy
(a)![]() w (3.2). Wtedy
krzywa punktów równowagi
w (3.2). Wtedy
krzywa punktów równowagi
pola ![]() na płaszczyżnie zmiennych
na płaszczyżnie zmiennych ![]() jest `pionowa' i
homeomorficzna z parabolą (patrz Rysunek 3.4). Również parabolą jest krzywa punktów równowagi
jest `pionowa' i
homeomorficzna z parabolą (patrz Rysunek 3.4). Również parabolą jest krzywa punktów równowagi ![]() dla pola
dla pola ![]()
W zależności od znaku ![]() kładziemy
kładziemy ![]() lub
lub ![]() czyli dalej można
zakładać, że obie `parabole' są zorientowane tak samo. W tym
przypadku konstrukcję homeomorfizmów
czyli dalej można
zakładać, że obie `parabole' są zorientowane tak samo. W tym
przypadku konstrukcję homeomorfizmów ![]() czyli
homeomorfizmu płaszczyzny
czyli
homeomorfizmu płaszczyzny
rozpoczynamy od konstrukcji homeomorfizmu pomiędzy krzywymi punktów równowagi: ![]() . Następnie przedłużamy
ten homeomorfizm do homeomorfizmu płaszczyzny, tak aby odcinki pionowe (w
. Następnie przedłużamy
ten homeomorfizm do homeomorfizmu płaszczyzny, tak aby odcinki pionowe (w ![]() poza punktami równowagi przechodziły na
odpowiednie odcinki pionowe. Jest raczej jasne, że tak da się zrobić.
poza punktami równowagi przechodziły na
odpowiednie odcinki pionowe. Jest raczej jasne, że tak da się zrobić.
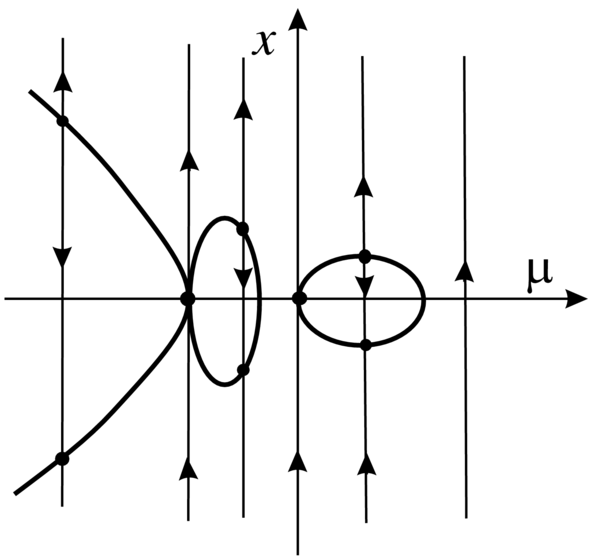
(b) W zdegenerowanym przypadku, gdy ![]() krzywa punktów równowagi
krzywa punktów równowagi ![]() może być bardzo
skomplikowana (patrz Rysunek 3.5). Ale wiemy, że z każdą prostą pionową
może być bardzo
skomplikowana (patrz Rysunek 3.5). Ale wiemy, że z każdą prostą pionową ![]() ta krzywa ma co najwyżej dwa
punkty przecięcia. Oznaczmy
ta krzywa ma co najwyżej dwa
punkty przecięcia. Oznaczmy ![]() przecięcie
przecięcie ![]() z
taką prostą. Zatem konstrukcja przeparametryzowania
z
taką prostą. Zatem konstrukcja przeparametryzowania ![]() polega na tym aby parametry
polega na tym aby parametry ![]() dla których
dla których ![]() przeszły na lewo od
przeszły na lewo od ![]() a parametry
a parametry ![]() dla których
dla których ![]() przeszły na prawo od
przeszły na prawo od ![]() (z zachowaniem ciągłości). Następnie, powtarzając
argumenty z przypadku (a), konstrujemy najpierw ciągłe przekształcenie
(z zachowaniem ciągłości). Następnie, powtarzając
argumenty z przypadku (a), konstrujemy najpierw ciągłe przekształcenie ![]() pomiędzy krzywymi
pomiędzy krzywymi ![]() i
i ![]() a następnie przedłużamy
je w sposób ciągły z zachowaniem pionowości.
a następnie przedłużamy
je w sposób ciągły z zachowaniem pionowości.
3.2. Transwersalność
Matematycznym aparatem do ścisłego sformułowania teorii bifurkacji i odpowiednich twierdzeń jest teoria transwersalności sformułowana przez francuskiego matematyka R. Thoma.
Niech ![]() będzie
będzie ![]() wymiarową rozmaitością a
wymiarową rozmaitością a ![]() będzie jej
będzie jej ![]() wymiarową podrozmaitością. Ponadto niech
wymiarową podrozmaitością. Ponadto niech ![]() będzie
będzie ![]() wymarową rozmaitością a
wymarową rozmaitością a
będzie odwzorowaniem różniczkowalnym (o wystarczającej
klasie różniczkowalności). W przypadku zwartych rozmaitości ![]() i
i ![]() w przestrzeni
w przestrzeni ![]() odwzorowań wprowadza się
naturalną topologię (której nie będę uściślał).
odwzorowań wprowadza się
naturalną topologię (której nie będę uściślał).
Definicja 3.4. Mówimy, że odwzorowanie ![]() jest transwersalne do podrozmaitości
jest transwersalne do podrozmaitości ![]() jeśli dla każdego
punktu
jeśli dla każdego
punktu ![]() takiego, że
takiego, że ![]() ma miejsce następująca własność
ma miejsce następująca własność
Gdy ![]() jest podrozmaitością i
jest podrozmaitością i ![]() jest włożeniem, to mówimy, że
jest włożeniem, to mówimy, że ![]() jest transwersalne do
jest transwersalne do ![]() gdy własność
gdy własność
zachodzi dla każdego punktu ![]() Mamy standardowe oznaczenia
Mamy standardowe oznaczenia
dla własności transwersalności.
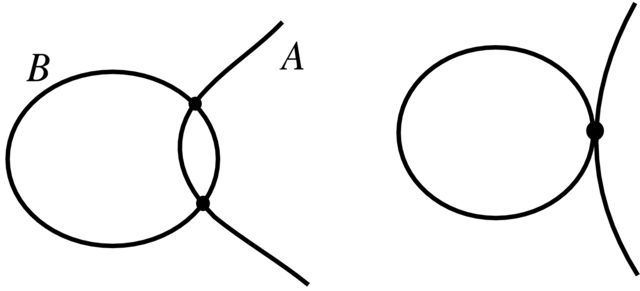
Przykład 3.5. (a) Niech ![]() oraz
oraz ![]() i
i ![]() będą gładkimi krzywymi. Wtedy
będą gładkimi krzywymi. Wtedy ![]() gdy
krzywa
gdy
krzywa ![]() przecina krzywę
przecina krzywę ![]() pod niezerowym kątem (patrz Rysunek
3.6).
pod niezerowym kątem (patrz Rysunek
3.6).
(b) Niech ![]()
![]() to krzywa i
to krzywa i ![]() to
powierzchnia. Rysunek 3.7 pokazuje przypadki transwersalności i
nietransweralsności.
to
powierzchnia. Rysunek 3.7 pokazuje przypadki transwersalności i
nietransweralsności.
(c) Przypadek ![]() i dwu powierzchni
i dwu powierzchni ![]() ,
, ![]() przedstawia Rysunek 3.8.
przedstawia Rysunek 3.8.
(d) Gdy ![]() i
i ![]()
![]() są krzywymi, to
są krzywymi, to ![]() wtedy i tylko wtedy gdy krzywe są rozłączne.
wtedy i tylko wtedy gdy krzywe są rozłączne.
(e) Niech ![]()
![]() i
i ![]() oraz niech
oraz niech ![]() będzie zadane wzorem
będzie zadane wzorem ![]() Oczywiście
Oczywiście ![]() tylko
dla
tylko
dla ![]() Ale wtedy
Ale wtedy ![]() Zatem
Zatem ![]() Ten przykład
pokazuje zasadność własności transwersalności odwzorowania
to podrozmaitości.
Ten przykład
pokazuje zasadność własności transwersalności odwzorowania
to podrozmaitości.
Zachodzi następujące fundamentalne twierdzenie pochodzące od
Thoma12To Twierdzenie Thoma o Transwersalności, jak również jego uogólnienie podane poniżej, stanowiły istotny element stworzonej
przez niego Teorii Katastrof . Ta teoria zawiera w sobie po części
teorię osobliwości odwzorowań i funkcji jak również teorię bifurkacji układów dynamicznych.
Warto jeszcze dodać, że w przypadku uogólnienia Twierdzenia
Thoma na przypadek rozmaitości niezwartych wprowadza się specjalną topologię (tzw. topologię Whitney'a) w przestrzeni odwzorowań klasy ![]() .
.
Twierdzenie 3.6 (Thom). Niech ![]()
![]() i
i ![]() będą ustalonymi zwartymi rozmaitościami jak powyżej. Wtedy podzbiór przestrzeni odwzorowań
będą ustalonymi zwartymi rozmaitościami jak powyżej. Wtedy podzbiór przestrzeni odwzorowań ![]() złożony z odwzorowań, które są transwersalne do
złożony z odwzorowań, które są transwersalne do ![]() jest otwarty i gęsty.
jest otwarty i gęsty.
To oznacza, że, z jednej strony, jeśli odwzorowanie ![]() jest transwersalne do
jest transwersalne do ![]() to dowolne bliskie niemu
odwzorowanie
to dowolne bliskie niemu
odwzorowanie ![]() też jest transwersalne do
też jest transwersalne do ![]() a, z drugiej strony, jeśli
a, z drugiej strony, jeśli ![]() nie jest
transwersalne, to dowolnie blisko niego istnieje odwzorowanie
nie jest
transwersalne, to dowolnie blisko niego istnieje odwzorowanie ![]() które już jest transwersalne.
które już jest transwersalne.
Dowód. Nietrudno zauważyć, że można ograniczyć się do sytuacji lokalnej, gdy ![]() i
i ![]() są podzbiorami otwartymi a
są podzbiorami otwartymi a
jest (lokalnie) podprzestrzenią kowymiaru ![]() (Zadanie 3.16).
(Zadanie 3.16).
Wtedy ![]() i
i
Jeśli ![]() , tzn.
, tzn. ![]() to
to ![]() jest transwersalne w
jest transwersalne w ![]() do
do ![]() wtedy i tylko wtedy gdy wektory
wtedy i tylko wtedy gdy wektory ![]() razem z
wektorami
razem z
wektorami ![]() rozpinają
rozpinają ![]() (Tutaj
(Tutaj ![]() i
i ![]() są
bazowymi wektorami w
są
bazowymi wektorami w ![]() i
i ![]() odpowiednio.) Do
tego wystarczy, aby rzuty wektorów
odpowiednio.) Do
tego wystarczy, aby rzuty wektorów ![]() na
przestrzeń ilorazową
na
przestrzeń ilorazową ![]() rozpinały tę przestrzeń. To oznacza, że macierz
rozpinały tę przestrzeń. To oznacza, że macierz
![C=\left[\begin{array}[]{ccc}\partial f_{{1}}/\partial x_{{1}}&\ldots&\partial f_{{1}}/\partial x_{{m}}\\
\ldots&\ldots&\ldots\\
\partial f_{{n-k}}/\partial x_{{1}}&\ldots&\partial f_{{n-k}}/\partial x_{{m}}\end{array}\right]](wyklady/rrj/mi/mi1326.png) |
ma rząd ![]()
Mamy dwie możliwości:
(i) ![]() i wtedy rząd jest mniejszy od
i wtedy rząd jest mniejszy od ![]()
(ii) ![]() (wtedy własność rk
(wtedy własność rk![]() jest warunkiem otwartym w przestrzeni macierzy).
W przypadku (i) transwersalność oznacza brak przecięcia
jest warunkiem otwartym w przestrzeni macierzy).
W przypadku (i) transwersalność oznacza brak przecięcia ![]() z
z ![]() i jest to warunek otwarty w przestrzeni odwzorowań. Również w przypadku (ii) nietrudno pokazać, że warunek transwersalności też jest otwarty (Zadanie 3.13).
i jest to warunek otwarty w przestrzeni odwzorowań. Również w przypadku (ii) nietrudno pokazać, że warunek transwersalności też jest otwarty (Zadanie 3.13).
Aby udowodnić gęstość własności transwersalności musimy wprowadzić dodatkowe pojęcia (Zadanie 3.14).
W przypadku (ii) weźmy lokalne odwzorowanie ![]()
Przypomnijmy (patrz Definicja 3.7 poniżej), że ![]() jest punktem
krytycznym dla
jest punktem
krytycznym dla ![]() jeśli rk
jeśli rk![]()
![]() rk
rk![]() a wartość
a wartość ![]() nazywa się wartością
krytyczną dla
nazywa się wartością
krytyczną dla ![]() . Skorzystamy z klasycznego Twierdzenia Sarda
(Twierdzenie 3.7 poniżej), które zapewnia, że zbiór wartości krytycznych dla
. Skorzystamy z klasycznego Twierdzenia Sarda
(Twierdzenie 3.7 poniżej), które zapewnia, że zbiór wartości krytycznych dla ![]() jest `rzadki'. Zgodnie z Zadaniem 3.15
jest `rzadki'. Zgodnie z Zadaniem 3.15 ![]() gdy
gdy ![]() nie jest wartością krytyczną dla
nie jest wartością krytyczną dla ![]() Niech
Niech ![]() będzie wartością niekrytyczną dla
będzie wartością niekrytyczną dla ![]() i bliską zeru. Zaburzymy odwzorowanie
i bliską zeru. Zaburzymy odwzorowanie ![]() w następujący sposób
w następujący sposób
Latwo sprawdzić, że ![]() jest transwersalne do
jest transwersalne do ![]() (Zadanie 3.16). ∎
(Zadanie 3.16). ∎
Definicja 3.7. Niech ![]() będzie odwzorowaniem różniczkowalnym. Mówimy, że że
będzie odwzorowaniem różniczkowalnym. Mówimy, że że ![]() jest punktem krytycznym dla
jest punktem krytycznym dla ![]() jeśli rk
jeśli rk![]() nie jest maksymalny. Wartość
nie jest maksymalny. Wartość ![]() w punkcie krytycznym nazywa się wartością
krytyczną dla
w punkcie krytycznym nazywa się wartością
krytyczną dla ![]()
Twierdzenie 3.8 (Sard). Zbiór wartości krytycznych
dla odwzorowania różniczkowalnego ![]() dostatecznie wysokiej klasy gładkości ma zerową miarę Lebesque'a.
dostatecznie wysokiej klasy gładkości ma zerową miarę Lebesque'a.
Uzasadnienie. Rozważmy przypadek ![]() . Nie jest wykluczone,
że wartości krytyczne dla
. Nie jest wykluczone,
że wartości krytyczne dla ![]() mogą tworzyć zbiór gęsty w
mogą tworzyć zbiór gęsty w ![]() .
.
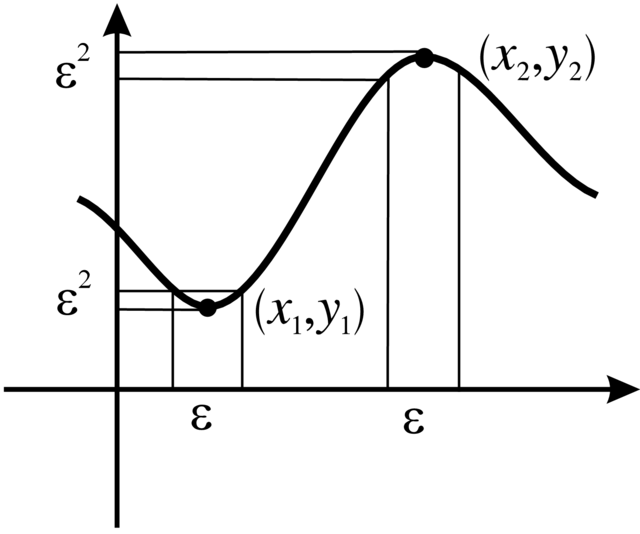
Możemy jednak pokryć każdy punkt krytyczny ![]() odcinkiem
odcinkiem ![]() o szerokości
o szerokości ![]() dla dowolnie małego
dla dowolnie małego ![]() Ponieważ
Ponieważ ![]() to długość obrazu
to długość obrazu ![]() takiego odcinka będzie szerokości rzędu
takiego odcinka będzie szerokości rzędu ![]() (patrz Rysunek 3.9). Zatem
(patrz Rysunek 3.9). Zatem
co dąży do zera przy ![]()
W istocie ten sam argument pracuje przy dowolnych ![]() (Zadanie 3.17).
Gdy
(Zadanie 3.17).
Gdy ![]() dowód jest bardziej skomplikowany (z rozbiciem
dowód jest bardziej skomplikowany (z rozbiciem ![]() na podzbiory stałego rzędu macierzy
na podzbiory stałego rzędu macierzy ![]() ∎
∎
Następująca definicja jest potrzebna do uogólnienia Twierdzenia Thoma. Niech
| (3.3) |
będzie odwzorowaniem dostatecznie wiele razy różniczkowalnym. Z takim odwzorowaniem można związać serię geometrycznych obiektów. Pierwszym z nich jest wykres
Innym jest wykres pochodnej, czyli wykres odwzorowania ![]()
Ogólnie, wykres odwzorowania ![]() tej pochodnej odwzorowania
tej pochodnej odwzorowania![]() jest podzbiorem (dosyć dużej) przestrzeni oznaczanej przez
jest podzbiorem (dosyć dużej) przestrzeni oznaczanej przez ![]()
Definicja 3.9. Przestrzenie ![]() nazywają się przestrzeniami dżetów rzędu
nazywają się przestrzeniami dżetów rzędu ![]() odzworowań z
odzworowań z ![]() do
do ![]() Z każdym
odzworowaniem postaci (3.3) wiąże się jego
Z każdym
odzworowaniem postaci (3.3) wiąże się jego ![]() ty dżet
ty dżet
Analogicznie, jeśli ![]() i
i ![]() są rozmaitościami wymiarów
są rozmaitościami wymiarów ![]() i
i ![]() odpowiednio, to definiuje się przestrzenie
odpowiednio, to definiuje się przestrzenie ![]() dżetów odwzorowań z
dżetów odwzorowań z ![]() do
do ![]() i z każdym różniczkowalnym odwzorowaniem
i z każdym różniczkowalnym odwzorowaniem ![]() wiąże się jego
wiąże się jego ![]() ty dżet
ty dżet ![]()
Definicja 3.10. Jeśli ![]() jest podrozmaitością, to mówimy, że odwzorowanie
jest podrozmaitością, to mówimy, że odwzorowanie ![]() jest
transwersalne do
jest
transwersalne do ![]() (oznaczenie
(oznaczenie ![]() gdy
gdy ![]()
Twierdzenie 3.11 (Thom). Niech ![]()
![]() i
i ![]() będą ustalone. Wtedy zbiór
odwzorowań
będą ustalone. Wtedy zbiór
odwzorowań ![]() które są transwersalne
do
które są transwersalne
do ![]() jest otwarty i gęsty w zbiorze wszystkich takich
odwzorowań.
jest otwarty i gęsty w zbiorze wszystkich takich
odwzorowań.
Dowód. Ten dowód w znacznej części powtarza dowód Twierdzenia 3.6. Podstawowa różnica leży w dowodzie gęstości, a dokładniej, w wyborze zaburzenia. Otóż, zamiast zamiany
![]() (gdzie
(gdzie ![]() jest `małą' wartością
niekrytyczną dla
jest `małą' wartością
niekrytyczną dla ![]() bierze się zamianę
bierze się zamianę ![]() gdzie
gdzie ![]()
![]()
![]() są odpowiednio `małymi' przekształeceniami liniowymi, jednorodnymi kwadratowymi, czy
jednorodnymi stopnia
są odpowiednio `małymi' przekształeceniami liniowymi, jednorodnymi kwadratowymi, czy
jednorodnymi stopnia ![]() ∎
∎
Przykład 3.12. Pewne naturalne warunki na odwzorowanie są interpretowane jako warunki na jego transwersalność w dżetach. Na przykład, warunek
wynika z jednoczesnej transwersalności odwzorowania
do dwóch podrozmaitości
Istotnie, transwersalność do ![]() oznacza, że
oznacza, że ![]() lub
lub ![]() gdy
gdy ![]() Tymczasem transweralność do
Tymczasem transweralność do ![]() oznacza,
że
oznacza,
że ![]() gdy
gdy ![]() i
i ![]()
W zagadnieniach teorii bifurkacji zawsze, gdy pojawiają się warunki
podobnego charakteru jak w Przykładzie 3.12, możemy założyć,
że albo są spełnione z prawdopodobieństwem 1 albo z takim
samym przwdopodobieństwem nie mogą być spełnione. Ten drugi
przypadek zachodzi gdy ![]() Taki jest praktyczny
wniosek z twierdzeń Thoma.
Taki jest praktyczny
wniosek z twierdzeń Thoma.
ZADANIA
Zadanie 3.13. W przypadku ![]() zauważyć, że (w
dowodzie Twierdzenia 3.6) rk
zauważyć, że (w
dowodzie Twierdzenia 3.6) rk![]() oznacza rk
oznacza rk![]() Skorzystać
z Twierdzenia o Funkcji Uwikłanej aby pokazać, że
Skorzystać
z Twierdzenia o Funkcji Uwikłanej aby pokazać, że ![]() w otoczeniu
w otoczeniu ![]() jest podrozmaitością w
jest podrozmaitością w ![]() kowymiaru
kowymiaru ![]() Pokazać następnie, że dla dowolnego
Pokazać następnie, że dla dowolnego ![]() bliskiego
bliskiego ![]() również
również ![]() jest lokalnie podrozmaitością kowymiaru
jest lokalnie podrozmaitością kowymiaru ![]() bliską
bliską ![]() Wywnioskować stąd i z otwartości podzbioru macierzy
rzędu
Wywnioskować stąd i z otwartości podzbioru macierzy
rzędu ![]() w przestrzeni macierzy wymiaru
w przestrzeni macierzy wymiaru ![]() że
że ![]() jest transwersalne do
jest transwersalne do ![]() w otoczeniu
w otoczeniu ![]()
Zadanie 3.14. Pokazać lokalną gęstość własności transwersalności w przypadku ![]()
Wskazówka: Wybrać odpowiednie zaburzenie ![]() dla
dla ![]() które nie jest transwersalne do
które nie jest transwersalne do ![]()
Zadanie 3.15. Pokazać, że ![]() wtedy i tylko
wtedy gdy
wtedy i tylko
wtedy gdy ![]() nie jest wartością krytyczną dla odwzorowania
nie jest wartością krytyczną dla odwzorowania ![]()
Zadanie 3.16. Uzupełnić dowód Twierdzenia 3.6.
Wskazówka: Użyć odpowiedniego rozkładu jedności ![]() w
w ![]() związanego z lokalnymi afinicznymi mapami w
związanego z lokalnymi afinicznymi mapami w ![]()
![]() i
i ![]() . Lokalne zaburzenia wybierać w postaci
. Lokalne zaburzenia wybierać w postaci ![]() z odpowiednimi funkcjami
z odpowiednimi funkcjami ![]() o zwartym nośniku i `małymi' wektorami
o zwartym nośniku i `małymi' wektorami ![]() Na koniec
skorzystać ze zwartości
Na koniec
skorzystać ze zwartości ![]()
Zadanie 3.17. Udowodnić Twierdzenie Sarda w przypadkach ![]() i
i
![]()
3.3. Bifurkacje kowymiaru 1
Bifurkacje autonomicznych pól wektorowych będziemy dzielić na lokalne i nielokalne.
Lokalne bifurkacje zachodzą w otoczeniu punktu osobliwego ![]() dla wartości bifurkacyjnej parametru. Dokładniej, mamy rodzinę
dla wartości bifurkacyjnej parametru. Dokładniej, mamy rodzinę
taką, że
W przypadku typowych ![]() parametrowych rodzin naruszenie warunku hi-
perboliczności (tzn.
parametrowych rodzin naruszenie warunku hi-
perboliczności (tzn. ![]() dla wszystkich
wartości własnych) zachodzi w dwu przypadkach:
dla wszystkich
wartości własnych) zachodzi w dwu przypadkach:
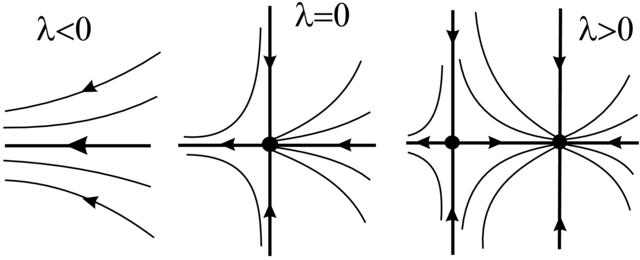
1. ![]() i
i ![]() dla
dla ![]() jest to bifurkacja siodło–węzeł.
jest to bifurkacja siodło–węzeł.
2. ![]() i
i ![]() dla
dla ![]() jest to bifurkacja
narodzin cyklu granicznego albo bifurkacja Andronowa–Hopfa.
jest to bifurkacja
narodzin cyklu granicznego albo bifurkacja Andronowa–Hopfa.
Mamy trzy nielokalne bifurkacje związane z orbitą okresową ![]() dla pola
dla pola ![]() Niech
Niech ![]() będą wartościami własnymi części liniowej przekształcenia powrotu
Poincarégo. Przypomnijmy, że warunek hiperboliczności dla
będą wartościami własnymi części liniowej przekształcenia powrotu
Poincarégo. Przypomnijmy, że warunek hiperboliczności dla ![]() oznacza, że
oznacza, że ![]() dla
wszystkich
dla
wszystkich ![]() Zatem typowe bifurkacje kowymiaru 1 mają miejsce w następujących przypadkach:
Zatem typowe bifurkacje kowymiaru 1 mają miejsce w następujących przypadkach:
3. ![]() i
i ![]() dla
dla ![]() jest to bifurkacja siodło–węzeł dla orbity
okresowej.
jest to bifurkacja siodło–węzeł dla orbity
okresowej.
4. ![]() i
i ![]() dla
dla ![]() jest to bifurkacja podwojenia okresu.
jest to bifurkacja podwojenia okresu.
5. ![]() Tutaj przypadki, gdy
Tutaj przypadki, gdy ![]() jest
pierwiastkiem z 1 stopnia
jest
pierwiastkiem z 1 stopnia ![]() nazywają się rezonansowymi; dodatkowo, gdy
nazywają się rezonansowymi; dodatkowo, gdy ![]() to mówimy o silnym rezonansie.
to mówimy o silnym rezonansie.
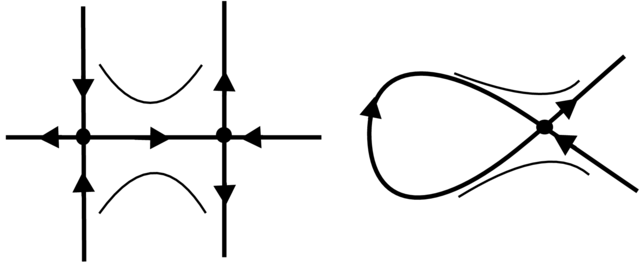
Na koniec mamy dwie nielokalne bifurkacje związane z połaczeniem separatrys (patrz Rysunek 3.10):
6. Połączenie separatrys różnych siodeł.
7. Pętla separatrys jednego siodła.
3.3.1. Redukcja do rozmaitości centralnej i forma normalna Poincarégo–Dulaca
Załóżmy, że mamy pole wektorowe
z punktem osobliwym ![]() Możemy założyć, że macierz
Możemy założyć, że macierz ![]() ma postać blokowo diagonalną
ma postać blokowo diagonalną
| (3.4) |
gdzie ![]() (odpowiednio
(odpowiednio ![]() i
i ![]() ma wartości własne z
ma wartości własne z ![]() (odpowiednio z
(odpowiednio z ![]() i z
i z ![]()
Twierdzenie 3.18 (Szoszitaiszwili). W sytuacji jak powyżej istnieje lokalny homeomorfizm ![]() przeprowadzający
portret fazowy pola
przeprowadzający
portret fazowy pola ![]() na portret fazowy następującego
pola
na portret fazowy następującego
pola
| (3.5) |
gdzie
Dowód tego twierdzenia jest techniczny i skomplikowany (patrz [5]). Dlatego nie będziemy go tutaj przytaczać. Za to wyciągniemy z niego bardzo praktyczne zastosowania. Zauważmy też, że to twierdzenie jest uogólnieniem Twierdzenia Grobmana–Hartmana.
Definicja 3.19. Podrozmaitość zadaną równaniem
(w terminach (3.5)) nazywamy rozmaitością centralną.
Twierszenie Szoszitaiszwiliego mówi, że w przypadku niehiperbolicznego puktu osobliwego `ciekawa część' dynamiki odbywa się na rozmaitości centralnej.
Dla rodziny pól wektorowych ![]() możemy potraktować
możemy potraktować ![]() jako dodatkową zmienną, tzn. mamy układ
jako dodatkową zmienną, tzn. mamy układ
do którego stosujemy Twierdzenie 3.18 (z ![]() Mamy następującą redukcję do rozmaitości
centralnej.
Mamy następującą redukcję do rozmaitości
centralnej.
Stwierdzenie 3.20. Dla rodziny ![]() z
z ![]()
![]() , istnieje lokalny homeomeorfizm
, istnieje lokalny homeomeorfizm ![]() zadajający topologiczną równoważność tej rodziny z następującą rodziną
zadajający topologiczną równoważność tej rodziny z następującą rodziną
Samo istnienie rozmaitości centralnej ![]() jest uogólnieniem
Twierdzenia Hadamarda–Perrona. Można jej poszukiwać jak w dwodzie
Twierdzenia 1.19. Przy tym okaże się, że rozmaitość
centralna nie jest wyznaczona jednoznacznie; zależy ona od wyboru przedłużenia pola (lub dyfeomorfizmu) na całe
jest uogólnieniem
Twierdzenia Hadamarda–Perrona. Można jej poszukiwać jak w dwodzie
Twierdzenia 1.19. Przy tym okaże się, że rozmaitość
centralna nie jest wyznaczona jednoznacznie; zależy ona od wyboru przedłużenia pola (lub dyfeomorfizmu) na całe ![]()
Ale istnieje sposób wyznaczenia ![]() w sposób formalny.
Poszukujemy jej jako wykresu
w sposób formalny.
Poszukujemy jej jako wykresu
(gdzie współrzędne ![]() są związane z rozkładem (3.4)), który jest niezmienniczy względem
pola
są związane z rozkładem (3.4)), który jest niezmienniczy względem
pola ![]() . Okazuje się, że odwzorowania
. Okazuje się, że odwzorowania ![]() i
i ![]() mają jednoznacznie wyznaczone szeregi
Taylora,
mają jednoznacznie wyznaczone szeregi
Taylora, ![]() Na
Na ![]() które jest parametryozwane przez
które jest parametryozwane przez ![]() otrzymujemy pole wektorowe
otrzymujemy pole wektorowe
Ta redukcja do ![]() nazywa się redukcją Lapunowa–Schmidta.
nazywa się redukcją Lapunowa–Schmidta.
Niestety, na ogół okazuje się, że szeregi zadające ![]() i
i
![]() są rozbieżne (nawet gdy
są rozbieżne (nawet gdy ![]() było analityczne). Tym też
tłumaczy się niejednoznaczność
było analityczne). Tym też
tłumaczy się niejednoznaczność ![]() w sensie topologicznym.
w sensie topologicznym.
Przykład 3.21. Rozważmy układ
Tutaj ![]() jest rozmaitością niestabilną. Rozmaitość centralną poszukujemy w postaci
jest rozmaitością niestabilną. Rozmaitość centralną poszukujemy w postaci ![]() Podstawiając takie
Podstawiając takie ![]() do układu, dostajemy
do układu, dostajemy
To prowadzi do następującej rekurencji: ![]()
![]() z rozwiązaniem
z rozwiązaniem ![]() Zatem rozmaitość centralna
zadaje się jednoznacznym, ale rozbieżnym, szeregiem
Zatem rozmaitość centralna
zadaje się jednoznacznym, ale rozbieżnym, szeregiem
(Zadania 3.27 i 3.28).
Innym narzędziem użytecznym w teorii bifurkacji, które również opiera się na (często rozbieżnych) szeregach formalnych, jest następne twierdzenie. Rozważamy kiełki analitycznych pól wektorowych
| (3.6) |
takich, że macierz ![]() jest diagonalna,
jest diagonalna, ![]() diag
diag![]() Przypomnijmy jeszcze standardowe
oznaczenia
Przypomnijmy jeszcze standardowe
oznaczenia ![]() dla standardowej basy w
dla standardowej basy w ![]() (zatem
(zatem ![]() ),
), ![]() i
i ![]()
Definicja 3.22. Mówimy, że wartości własne spełniają relację rezonansową typu ![]()
![]()
![]() jeśli
jeśli
Twierdzenie 3.23 (Poincaré–Dulac). Załóżmy że mamy kiełek zespolonego analitycznego pola wektorowego (3.6). Wtedy istnieje zamiana
taka, że każda składowa po prawej stronie jest formalnym
szeregiem potęgowym od ![]() która prowadzi do układu
która prowadzi do układu
| (3.7) |
przy czym sumy po prawych stronach równań (3.7) biegną
po takich wielowskaźnikach ![]() że jest spełniona relacja rezonansowa typu
że jest spełniona relacja rezonansowa typu ![]()
Dowód. Sprowadzanie do postaci normalnej Poincarégo–Dulaca (3.7) odbywa się przy pomocy serii zamian postaci
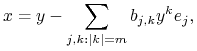 |
(3.8) |
czyli dodajemy wyrazy jednorodne stopnia ![]() (Zaczynamy od
(Zaczynamy od ![]() potem
bierzemy
potem
bierzemy ![]() itd.) Łatwo sprawdzić, że przekształcenie
odwrotne do (3.8) ma postać
itd.) Łatwo sprawdzić, że przekształcenie
odwrotne do (3.8) ma postać ![]() (Zadanie 3.29).
(Zadanie 3.29).
Załóżmy, że w polu (3.6) do stopnia ![]() występują
tylko wyrazy rezonansowe (założenie indukcyjne). Chcemy przy pomocy
podstawienia (3.8) zlikwidować wyrazy nierezonansowe stopnia dokładnie
występują
tylko wyrazy rezonansowe (założenie indukcyjne). Chcemy przy pomocy
podstawienia (3.8) zlikwidować wyrazy nierezonansowe stopnia dokładnie
![]() Mamy
Mamy
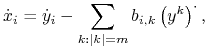 |
(3.9) |
gdzie
i
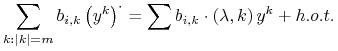 |
Z lewej strony wzoru (3.9), po podstawieniu (3.8), mamy
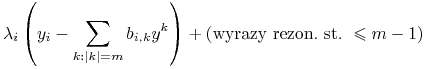 |
||||
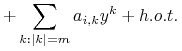 |
Teraz, porównując wyrazy jednorodne stopnia ![]() dostajemy równania
dostajemy równania
Z nich jasno wynika, że jeśli ![]() , to można dobrać
, to można dobrać ![]() tak, aby zlikwidować
odpowiedni nierezonansowy wyraz
tak, aby zlikwidować
odpowiedni nierezonansowy wyraz ![]() . Pozostają tylko wyrazy
rezonansowe. ∎
. Pozostają tylko wyrazy
rezonansowe. ∎
Przykład 3.24. Rozważmy przypadek rezonansowego węzła
czyli dla ![]() i
i ![]() Jak
łatwo stwierdzić, jedyną relacją rezonansową jest
Jak
łatwo stwierdzić, jedyną relacją rezonansową jest ![]() Zatem normalna forma Poincarégo–Dulaca jest następująca
Zatem normalna forma Poincarégo–Dulaca jest następująca
(Zadanie 3.30). Okazuje się, że w tym przypadku zamiana prowadząca do postaci normalnej jest analityczna (o ile wyjściowy kiełek był analityczny). 13Do tego przypadku można też zaliczyć sytuację, gdy ![]() czyli, gdy część liniowa nie jest diagonalna. Istnieje naturale
rozszerzenie Twierdzenia 3.23 na przypadek, gdy część linowa
pola posiada nietrywialne klatki Jordana.
czyli, gdy część liniowa nie jest diagonalna. Istnieje naturale
rozszerzenie Twierdzenia 3.23 na przypadek, gdy część linowa
pola posiada nietrywialne klatki Jordana.
Przykład 3.25. Dla siodło–węzła
czyli z ![]() i
i ![]() , relacje rezonasowe są
postaci
, relacje rezonasowe są
postaci ![]() i
i ![]() Stąd wynika następująca
forma Poincarégo–Dulaca
Stąd wynika następująca
forma Poincarégo–Dulaca
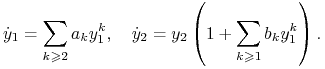 |
Okazuje się, że na ogół ta forma normalna nie jest analityczna.
Przykład 3.26.Dla ![]() rezonansowego siodła
rezonansowego siodła
czyli z ![]() i
i ![]() relacje rezonansowe są
postaci
relacje rezonansowe są
postaci ![]() i
i ![]() Stąd wynika następująca
postać normalna Poincarégo–Dulaca
Stąd wynika następująca
postać normalna Poincarégo–Dulaca
Również i ta forma nie jest na ogól analityczna (Zadanie 3.31).
ZADANIA
Zadanie 3.27. Znaleźć rozmaitość centralną
punktu ![]() dla układu z Zadania 1.33 przy
dla układu z Zadania 1.33 przy ![]() tzn.
dla
tzn.
dla ![]()
![]()
Zadanie 3.28. Znaleźć przybliżenie rozmaitości
centralnej z dokładnością do wyrazów sześciennych dla
punktu ![]() układu
układu ![]()
![]()
![]()
Zadanie 3.29. Pokazać, że przekształcenie odwrotne do przekształcenia (3.8) ma postać jak w dowodzie Twierdzenia 3.23.
Zadanie 3.30. Pokazać, że w każdym innym przypadku węzła, tzn. gdy ![]() normalna forma Poincarégo–Dulaca jest liniowa (brak nieliniowych wyrazów rezonansowych).
normalna forma Poincarégo–Dulaca jest liniowa (brak nieliniowych wyrazów rezonansowych).
Zadanie 3.31. Uogólnić Przykład 3.26 na przypadek ![]() rezonansowego siodła, tzn. gdy
rezonansowego siodła, tzn. gdy ![]() (ułamek zredukowany).
(ułamek zredukowany).
3.3.2. Bifurkacja siodło–węzeł
Mamy ![]() parametrową rodzinę pól wektorowych
parametrową rodzinę pól wektorowych
Na nią nakładamy następujące warunki:
1. ![]() i
i ![]()
2. Macierz ![]() ma jedną zerową wartość własną,
ma jedną zerową wartość własną,
![]() (w szczególności
(w szczególności ![]() i
i ![]() dla
dla ![]() Zatem można założyć, że
Zatem można założyć, że ![]() ma
postać blokową
ma
postać blokową
3. Niech ![]() będzie liniowym układem współrzędnych związanym z powyższą postacią
będzie liniowym układem współrzędnych związanym z powyższą postacią ![]() Możemy przepisać układ w postaci
Możemy przepisać układ w postaci
gdzie ![]() i
i ![]()
![]() Następne założenie mówi, że
Następne założenie mówi, że
4. Ostatnie założenie mówi, że
(Zadanie 3.34).
Uwaga 3.32. Powyższe warunki są warunkami w przestrzeni ![]() dżetów
rzędu 2. Są to warunki na transwersalność względem
pewnych podrozmaitości w
dżetów
rzędu 2. Są to warunki na transwersalność względem
pewnych podrozmaitości w ![]() Dzięki Twierdzeniu 3.11 typowe
Dzięki Twierdzeniu 3.11 typowe ![]() spełnia te warunki (porównaj też Przykład 3.12).
spełnia te warunki (porównaj też Przykład 3.12).
Twierdzenie 3.33.Jeśli są spełnione powyższe
warunki, to rodzina ![]() jest wersalna. W
szczególności, jest ona równoważna jednej z rodzin postaci
jest wersalna. W
szczególności, jest ona równoważna jednej z rodzin postaci
Dowód. Z twierdzenia o redukcji do rozmaitości centralnej możemy założyć, że mamy układ postaci
Mamy następujące własności wynikające bezpośrednio z Warunków 1, 2, 3 i 4:
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv) ![]()
Dalszy dowód przebiega dokładnie jak w Przykładzie 3.3.
Na Rysunku 3.11 jest przedstawiona bifurkacja siodło–węzeł dla rodziny dwuwymiarowych pól wektorowych. ∎
ZADANIA
Zadanie 3.34. Pokazać, że Warunek 4 posiada następującą interpretację. Z Warunku 3 wynika, że równanie ![]() posiada jednoznaczne rozwiązanie
posiada jednoznaczne rozwiązanie ![]() (punkt lokalnego extremum). Niech
(punkt lokalnego extremum). Niech ![]() (wartość w tego ekstremum). Wtedy
(wartość w tego ekstremum). Wtedy ![]()
![]()
![]()
Zadanie 3.35. Dla ![]() parametrowej rodziny
parametrowej rodziny ![]() wymiarowych pól
wektorowych
wymiarowych pól
wektorowych ![]() (deformacja osobliwości typu siodło–węzeł kowymiaru 2) zbadać bifurkacje punktów równowagi.
(deformacja osobliwości typu siodło–węzeł kowymiaru 2) zbadać bifurkacje punktów równowagi.
3.3.3. Bifurkacja Andronowa–Hopfa
Mamy ![]() parametrową rodzinę pól wektorowych
parametrową rodzinę pól wektorowych
Na nią nakładamy następujące warunki:
1. ![]() zatem
zatem ![]()
2. ![]() i
i ![]() dla
dla ![]() To implikuje
To implikuje ![]() i z
Twierdzenia o Funkcjach Uwikłanych równanie
i z
Twierdzenia o Funkcjach Uwikłanych równanie ![]() ma rozwiązanie
ma rozwiązanie ![]() które odpowiada punktowi równowagi. Następnie przesuwamy ten punkt równowagi do początku układu współrzędnych:
które odpowiada punktowi równowagi. Następnie przesuwamy ten punkt równowagi do początku układu współrzędnych: ![]() Teraz mamy układ
Teraz mamy układ
3. Następne założenie mówi, że
4. Ostatnie założenie wykorzystuje formę normalną
Poincarégo–Dulaca dla ![]() W dziedzinie zespolonej mamy
W dziedzinie zespolonej mamy ![]() i zgodnie z Przykładem 3.26 forma normalna przyjmuje
postać
i zgodnie z Przykładem 3.26 forma normalna przyjmuje
postać
gdzie ![]() są
(formalnymi) zmiennymi zespolonymi po ograniczniu do rozmaitości
centralnnej. Ponieważ wyjściowe pole było rzeczywiste, to
są
(formalnymi) zmiennymi zespolonymi po ograniczniu do rozmaitości
centralnnej. Ponieważ wyjściowe pole było rzeczywiste, to ![]() i powyższe równania są względem siebie sprzężone. W zmiennych rzeczywistych
i powyższe równania są względem siebie sprzężone. W zmiennych rzeczywistych ![]() i
i ![]() dostajemy następującą postać
normalną Poincarégo–Dulaca dla ogniska
dostajemy następującą postać
normalną Poincarégo–Dulaca dla ogniska
gdzie ![]() Tutaj
Tutaj ![]() są
liczbami ogniskowymi Lapunowa–Poincarego z Definicji 2.13 (Zadanie 3.40).
są
liczbami ogniskowymi Lapunowa–Poincarego z Definicji 2.13 (Zadanie 3.40).
Ostatni warunek niezdegenerowania mówi, że
Następujące twierdzenie nosi też nazwę Twierdzenia o narodzinach cyklu granicznego i jest najbardziej chyba znanym twierdzeniem z teorii bifurkacji.
Twierdzenie 3.36 (Andronov–Hopf). Jeśli są spełnione powyższe warunki, to rodzina ![]() jest wersalna. W szczególności jest ona równoważna
rodzinie
jest wersalna. W szczególności jest ona równoważna
rodzinie
(![]() lub (równoważnie i
na rozmaitości centralnej) rodzinie
lub (równoważnie i
na rozmaitości centralnej) rodzinie
| (3.10) |
Uwaga 3.37. Z dokładnością do zmiany orientacji płaszczyzny (np. ![]() można przyjąć, że
częstotliwość
można przyjąć, że
częstotliwość ![]() Przy tym założeniu mamy dwie
lokalne bifurkacje rodzin (3.10) odpowiadających dwu wartościom
Przy tym założeniu mamy dwie
lokalne bifurkacje rodzin (3.10) odpowiadających dwu wartościom ![]() i
i ![]() Są one przedstawione na Rysunkach 3.12 i 3.13
odpowiednio. Różnica pomiędzy tymi rysunkami ma istotne
znaczenie praktyczne.
Są one przedstawione na Rysunkach 3.12 i 3.13
odpowiednio. Różnica pomiędzy tymi rysunkami ma istotne
znaczenie praktyczne.
Na Rysunku 3.12 obserwujemy tzw. ostrą utratę stabilności. Istotnie, dla ![]() punkt równowagi jest stabilny (chociaż
`basen' jego przyciągania kurczy się) a dla
punkt równowagi jest stabilny (chociaż
`basen' jego przyciągania kurczy się) a dla ![]() punkt równowagi staje się `globalnie' niestabilny (tutaj układ kompletnie
się rozstraja).
punkt równowagi staje się `globalnie' niestabilny (tutaj układ kompletnie
się rozstraja).
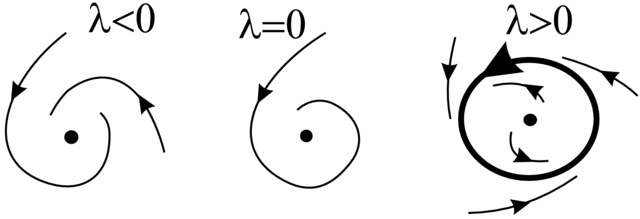
Na Rysunku 3.13 mamy do czynienia z tzw. łagodną utratą
stabilności. Dla ![]() punkt równowagi jest `globalnie'
stabilny i dla
punkt równowagi jest `globalnie'
stabilny i dla ![]() traci on stabilność. Ale dla
traci on stabilność. Ale dla ![]() pojawia się stabilny cykl graniczny, zlokalizowany blisko punktu równowagi. Zatem układ (np. mechaniczny) zaczyna lekko oscylować wokół położenia równowagi.
pojawia się stabilny cykl graniczny, zlokalizowany blisko punktu równowagi. Zatem układ (np. mechaniczny) zaczyna lekko oscylować wokół położenia równowagi.
Dowód Twierdzenia 3.36. Podobnie jak w przypadku Twierdzenia o Bifurkacji Siodło–Węzeł sprowadzamy najpierw zagadnienie do sytuacji dwuwymiarowej (na rozmaitości centralnej).
Lekko uzupełniając dowód Twierdzenia Poincarégo–Dulaca
sprowadzamy całą rodzinę do następującej postaci
normalnej, modulo wyrazy rzędu ![]()
| (3.11) |
![]() gdzie
gdzie ![]()
![]() i
i ![]() (Zadanie 3.41). Możemy spokojnie przyjąć, że
(Zadanie 3.41). Możemy spokojnie przyjąć, że ![]() i, przechodząc do biegunowego układu współrzędnych,
i, przechodząc do biegunowego układu współrzędnych, ![]() możemy napisać
możemy napisać
| (3.12) |
(Zadanie 3.42).
Dla układu (3.12) definiujemy przekształcenie powrotu Poincarégo ![]()
![]() jak na Rysunku 3.14. Dla ustalenia uwagi założymy, że
jak na Rysunku 3.14. Dla ustalenia uwagi założymy, że ![]() Dalszą analizę dzielimy na trzy kroki.
Dalszą analizę dzielimy na trzy kroki.
(a) Dla ![]() mamy
mamy ![]() (dla
(dla ![]() czyli
czyli ![]() i nie ma cykli granicznych.
i nie ma cykli granicznych.
(b) Niech ![]() . Rozważmy obszar
. Rozważmy obszar ![]() Dokonajmy następującej normalizacji
Dokonajmy następującej normalizacji
Wtedy w obszarze ![]() dostajemy układ
dostajemy układ
| (3.13) |
dla małego parametru ![]() Teraz już łatwo wyliczyć przekształcenie
Teraz już łatwo wyliczyć przekształcenie ![]() Zauważmy, że rozwiązanie układu (3.13)
z warunkiem początkowym
Zauważmy, że rozwiązanie układu (3.13)
z warunkiem początkowym ![]()
![]() spełnia
spełnia ![]() Zatem
Zatem
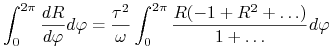 |
||||
Oznaczmy ![]() gdzie wykres funkcji
gdzie wykres funkcji ![]() jest
przedstawiony na Rysunku 3.15. Widzimy, że równanie
jest
przedstawiony na Rysunku 3.15. Widzimy, że równanie ![]() posiada dokładnie dwa proste rozwiązania
posiada dokładnie dwa proste rozwiązania ![]() i
i ![]() (Zadanie 3.43). Pierwsze z nich odpowiada punktowi równowagi, a drugie cyklowi granicznemu bliskiemu okręgu
(Zadanie 3.43). Pierwsze z nich odpowiada punktowi równowagi, a drugie cyklowi granicznemu bliskiemu okręgu ![]()
(c) Dla ![]() rozważmy obszar
rozważmy obszar ![]() dla małego
dla małego ![]() (niezależnego
od
(niezależnego
od ![]() Z (3.12) łatwo widać, że tutaj
Z (3.12) łatwo widać, że tutaj ![]() i nie może być cykli granicznych.
i nie może być cykli granicznych.
Widać zatem, że w każdej z trzech powyższych sytuacji
portrety fazowe są `jakościowo' takie same jak dla modelowej rodziny
(3.10). Wypadałoby jeszcze skonstruować rodzinę ![]() lokalnych homeomorfizmów realizujących topologiczne
orbitalne równoważności odpowiednich portretów fazowych.
Jest to dosyć żmudne zadanie (jeśli potraktować je bardzo
serio) i my je opuścimy (nawet w [5] jest to pominięte). ∎
lokalnych homeomorfizmów realizujących topologiczne
orbitalne równoważności odpowiednich portretów fazowych.
Jest to dosyć żmudne zadanie (jeśli potraktować je bardzo
serio) i my je opuścimy (nawet w [5] jest to pominięte). ∎
Uwaga 3.38. E. Hopf w swojej oryginalnej pracy udowodnił ogólniejsze wynik niż Twierdzenie 3.36. Mianowicie opuścił on założenie, że ![]() (patrz [14]). Pokazał on istnienie
(patrz [14]). Pokazał on istnienie ![]() parametrowej rodziny
parametrowej rodziny ![]() rozwiązań okresowych dla pól wektorowych
rozwiązań okresowych dla pól wektorowych ![]() gdzie
gdzie ![]() jest pewnym gładkim
odwzorowaniem. To twierdzenie nazywa się Twierdzeniem o
Bifurkacji Hopfa. Na przykład, dla rodziny
jest pewnym gładkim
odwzorowaniem. To twierdzenie nazywa się Twierdzeniem o
Bifurkacji Hopfa. Na przykład, dla rodziny
mamy rodzinę rozwiązań okresowych ![]() dla jednego pola
dla jednego pola ![]() tzn.
tzn. ![]()
Arnold [5] często podkreślał, że w przypadku ![]() odpowiednią bifurkację badał równolegle A. Andronov [2].
Dlatego też bifurkacja z Twierdzenia 3.36 nazywa się Bifurkacją Andronowa–Hopfa.
odpowiednią bifurkację badał równolegle A. Andronov [2].
Dlatego też bifurkacja z Twierdzenia 3.36 nazywa się Bifurkacją Andronowa–Hopfa.
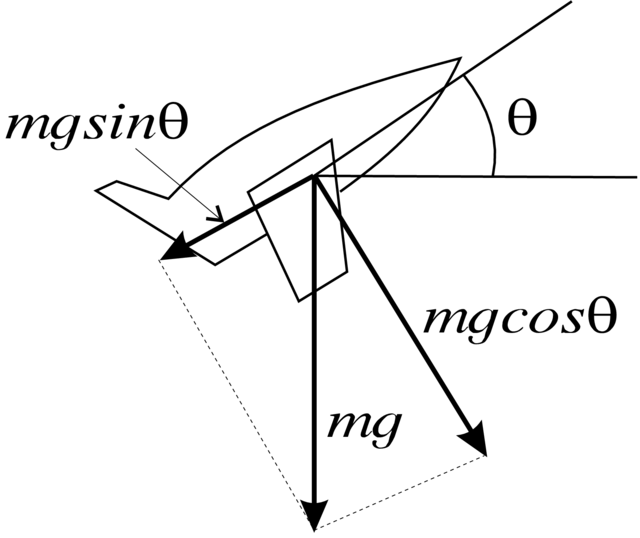
Przykład 3.39 (Model Żukowskiego szybowca). Niech samolot
leci z prędkością ![]() (która może się zmieniać)
i jest podniesiony pod kątem
(która może się zmieniać)
i jest podniesiony pod kątem ![]() względem poziomu (patrz
Rysunek 3.16). Na samolot działają następujące siły: siła
ciągu
względem poziomu (patrz
Rysunek 3.16). Na samolot działają następujące siły: siła
ciągu ![]() skierowana wzdłuż samolotu, siła ciężkości
skierowana wzdłuż samolotu, siła ciężkości ![]() skierowana do dołu i siła oporu powietrza proporcjonalna do
skierowana do dołu i siła oporu powietrza proporcjonalna do
![]() . Rozkładamy siłę ciężkości na składową wzdłuż samolotu (powodującą wytracanie prędkości) i w
kierunku prostopadłym (powodując obrót w dół). Mamy zatem
następującą parę równań:
. Rozkładamy siłę ciężkości na składową wzdłuż samolotu (powodującą wytracanie prędkości) i w
kierunku prostopadłym (powodując obrót w dół). Mamy zatem
następującą parę równań: ![]() i
i ![]() Tutaj stałe
Tutaj stałe ![]() i
i ![]() zależą od kilku czynników, których
nie będę specyfikował (patrz [8], Rozdz. 3, Paragr. 3) i [7],
Rozdz. 14, Paragr. 3, Rozdz. 15, Paragr. 3). Po odpowiedniej normalizacji
zależą od kilku czynników, których
nie będę specyfikował (patrz [8], Rozdz. 3, Paragr. 3) i [7],
Rozdz. 14, Paragr. 3, Rozdz. 15, Paragr. 3). Po odpowiedniej normalizacji ![]() dostajemy następującą
dostajemy następującą ![]() parametrową rodzinę pól wektorowych
parametrową rodzinę pól wektorowych
| (3.14) |
![]() ,
, ![]() z biegunem wzdłuż
z biegunem wzdłuż ![]()
Rozważmy najpierw przypadek ![]() który odpowiada modelowi
szybowca. Po pomnożeniu przez
który odpowiada modelowi
szybowca. Po pomnożeniu przez ![]() (przeskalowanie czasu) dostajemy
portret fazowy regularnego pola
(przeskalowanie czasu) dostajemy
portret fazowy regularnego pola
| (3.15) |
Przy ![]() dostajemy układ hamiltonowski z całką pierwszą
dostajemy układ hamiltonowski z całką pierwszą
i punktami równowagi ![]() i
i ![]() . Przy
. Przy ![]() dostajemy
dostajemy ![]() czyli
funkcja
czyli
funkcja ![]() jest funkcją Dulaca dla pola (3.14). Stąd łatwo
wynika, że dla
jest funkcją Dulaca dla pola (3.14). Stąd łatwo
wynika, że dla ![]() ruch szybowca jest okresowy (oscylujący wokół centrum
ruch szybowca jest okresowy (oscylujący wokół centrum ![]() ) a dla
) a dla ![]() odpowiedni punkt krytyczny
odpowiedni punkt krytyczny ![]() (bifurkujący z
(bifurkujący z ![]() jest globalnie stabilnym ogniskiem
(Zadanie 3.44). To znaczy, że ruch szybowca stabilizuje się.
jest globalnie stabilnym ogniskiem
(Zadanie 3.44). To znaczy, że ruch szybowca stabilizuje się.
Dla ogólnej rodziny (3.14) z małymi ![]() i
i ![]() można
badać pojawiające się możliwe cykle graniczne metodą całek abelowych (patrz Przykład 4.5 poniżej). Przyrost
można
badać pojawiające się możliwe cykle graniczne metodą całek abelowych (patrz Przykład 4.5 poniżej). Przyrost ![]() całki pierwszej wzdłuż trajektorii układu (3.14) (od cięcia do cięcia) wynosi w przybliżeniu
całki pierwszej wzdłuż trajektorii układu (3.14) (od cięcia do cięcia) wynosi w przybliżeniu
gdzie ![]() jest polem obszaru zakreślonego przez
krzywą
jest polem obszaru zakreślonego przez
krzywą![]() W [7] pokazano, że funkcja
W [7] pokazano, że funkcja ![]() jest monotoniczna, czyli, że równanie
jest monotoniczna, czyli, że równanie ![]() ma co najwyżej jedno rozwiązanie. To oznacza, że układ (4.14) dla małych
ma co najwyżej jedno rozwiązanie. To oznacza, że układ (4.14) dla małych ![]() i
i ![]() może posiadać co najwyżej jeden cykl graniczny.
może posiadać co najwyżej jeden cykl graniczny.
Tutaj w momencie, gdy dywergencja pola (3.14) w ognisku ![]() jest zerowa,
zachodzi bifurkacja Andronowa–Hopfa. Można sprawdzić, że jest
ona niezdegenerowana (zachęcam czytelników do sprawdzenia tego).
jest zerowa,
zachodzi bifurkacja Andronowa–Hopfa. Można sprawdzić, że jest
ona niezdegenerowana (zachęcam czytelników do sprawdzenia tego).
ZADANIA
Zadanie 3.40. Pokazać, że współczynniki ![]() z Punktu 4 założeń do Twierdzenia
Andronowa–Hopfa pokrywają się ze liczbami oniskowymi
Lapunowa–Poincarégo z Definicji 2.13. Znaleźć zależność pomiędzy wspólczynnikami
z Punktu 4 założeń do Twierdzenia
Andronowa–Hopfa pokrywają się ze liczbami oniskowymi
Lapunowa–Poincarégo z Definicji 2.13. Znaleźć zależność pomiędzy wspólczynnikami ![]() i
i ![]() a
a ![]() i
i
![]()
Zadanie 3.41. Udowodnić wzór (3.11).
Wskazówka: Redukcję skończonej liczby wyrazów rezonansowych
można przeprowadzać jednocześnie dla ![]() parametrowej rodziny.
parametrowej rodziny.
Zadanie 3.42. Udowodnić wzór (3.12).
Zadanie 3.43. Pokazać ściśle, że równanie ![]() z dowodu Twierdzenia 3.36 ma dokładnie dwa rozwiązania.
z dowodu Twierdzenia 3.36 ma dokładnie dwa rozwiązania.
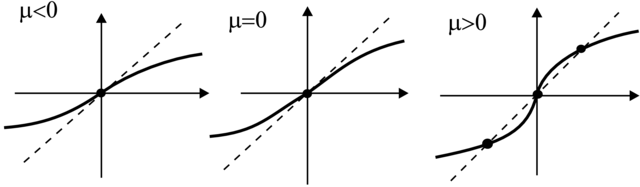
Zadanie 3.44. Zbadać punkty osobliwe pola (3.15). Naszkicować portrety fazowe dla ![]() i
i ![]()
3.3.4. Bifurkacje dla cykli granicznych
Niech ![]() będzie zamknniętą krzywą fazową
dla pola wektorowego
będzie zamknniętą krzywą fazową
dla pola wektorowego ![]() na rozmaitości
na rozmaitości ![]() (
(![]() wymiarowej).
Ponadto pole
wymiarowej).
Ponadto pole ![]() jest zanurzone w
jest zanurzone w ![]() parametrowej rodzinie
parametrowej rodzinie ![]()
![]() pól wektorowych
na
pól wektorowych
na ![]() Weźmy cięcie
Weźmy cięcie ![]() transwersalne do
transwersalne do ![]() w
w ![]() Dla
Dla ![]() bliskich
bliskich ![]() mamy dobrze zdefiniowane przekształcenia Poincarégo
mamy dobrze zdefiniowane przekształcenia Poincarégo ![]() Utożsamiając
Utożsamiając ![]() z
z ![]() otrzymujemy rodzinę lokalnych przekształceń
otrzymujemy rodzinę lokalnych przekształceń
takich, że ![]() Zatem
Zatem
Zakładamy też, że dla ![]() orbita
orbita ![]() jest
niehiperboliczna, tzn. punkt stały
jest
niehiperboliczna, tzn. punkt stały ![]() dyfeomorfizmu
dyfeomorfizmu ![]() jest
niehiperboliczny. W zależności od typu niehiperboliczności mamy różne rodzaje bifurkacji. My omówimy tutaj tylko dwie.
jest
niehiperboliczny. W zależności od typu niehiperboliczności mamy różne rodzaje bifurkacji. My omówimy tutaj tylko dwie.
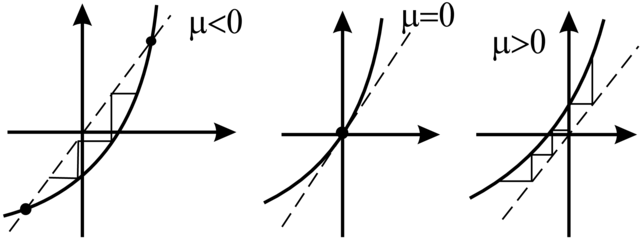
A. Bifurkacja siodło–węzeł dla cyklu granicznego. Tutaj
mamy ![]() i
i ![]()
![]() dla wartości własnych macierzy
dla wartości własnych macierzy ![]() Sprowadzając sytuację
do rozmaitości centralnej (czyli
Sprowadzając sytuację
do rozmaitości centralnej (czyli ![]() wymiarowej dla dyfeomorfizmu) i nakładając odpowiednie warunki niezdegenerowania (tzn.
wymiarowej dla dyfeomorfizmu) i nakładając odpowiednie warunki niezdegenerowania (tzn. ![]()
![]() pokazuje się równoważność odpowiedniej rodziny
pokazuje się równoważność odpowiedniej rodziny ![]() wymiarowych przekształceń z następującą modelową rodziną
wymiarowych przekształceń z następującą modelową rodziną
Odpowiednie bifurkacje są przedstawione na Rysunku 3.17. Widzimy, że dla ![]() mamy dwa cykle graniczne, które się zlewają przy
mamy dwa cykle graniczne, które się zlewają przy
![]() a następnie znikają.
a następnie znikają.
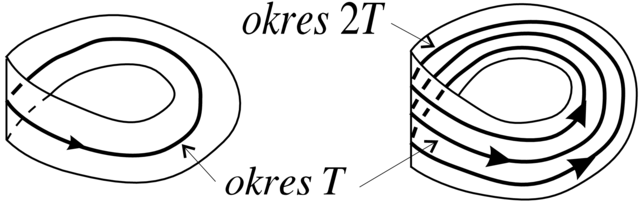
B. Bifurkacja podwojenia okresu. Tutaj mamy ![]() i
i ![]() dla
dla ![]() Ponieważ
przekształcenie powrotu zmienia orientację, to rozmaitość
centralna dla orbity
Ponieważ
przekształcenie powrotu zmienia orientację, to rozmaitość
centralna dla orbity ![]() jest wstęgą Möbiusa (patrz
Rysunek 3.19).
jest wstęgą Möbiusa (patrz
Rysunek 3.19).
Modelową rodziną przekształceń w tym przypadku jest
Oczywiście to przekształcenie ma tylko jeden punkt stały, tj. ![]() Ale jego druga iteracja ma postać
Ale jego druga iteracja ma postać
i posiada dwa dodatkowe punkty stałe ![]() dla
dla ![]() Te punkty stałe odpowiadają orbicie okresowej dla
Te punkty stałe odpowiadają orbicie okresowej dla ![]() o okresie 2. Stąd bierze się nazwa bifurkacji; czasami też
jest używana nazwa bifurkacja widełki (od kształtu krzywej
punktów okresowych na płaszczyźnie
o okresie 2. Stąd bierze się nazwa bifurkacji; czasami też
jest używana nazwa bifurkacja widełki (od kształtu krzywej
punktów okresowych na płaszczyźnie ![]()
Odpowiednie bifurkacje dla ![]() są przedstawione
na Rysunku 3.18.14Bifurkacja podwojenia okresu leży u podstaw znanej bifurkacji
Feigenbauma dla nieodwracalnego przekształcenia
są przedstawione
na Rysunku 3.18.14Bifurkacja podwojenia okresu leży u podstaw znanej bifurkacji
Feigenbauma dla nieodwracalnego przekształcenia ![]() odcinka
w siebie. Najpierw punkt stały traci stabilność przy przechodzeniu
wartości własnej przez
odcinka
w siebie. Najpierw punkt stały traci stabilność przy przechodzeniu
wartości własnej przez ![]() Potem powstała obrita okresowa o
okresie 2 znowu traci stabilność i powstaje orbita okresowa o
okresie 2
Potem powstała obrita okresowa o
okresie 2 znowu traci stabilność i powstaje orbita okresowa o
okresie 2![]() itd. Dla granicznej wartości parametru mamy bifurkację Feigenbauma.
itd. Dla granicznej wartości parametru mamy bifurkację Feigenbauma.