Zagadnienia
5. Chaotyczna dynamika w równaniach różniczkowych
5.1. Wstęp do teorii chaosu i jeden przykład
Dla autonomicznego pola wektorowego w ![]() portret fazowy i ruch
jest w pełni zdeterminowany; to zostało opisane w Rozddziale 2.4. Ale
gdy przestrzeń fazowa nie jest tak prosta, to mogą się zdarzać ciekawe zjawiska.
portret fazowy i ruch
jest w pełni zdeterminowany; to zostało opisane w Rozddziale 2.4. Ale
gdy przestrzeń fazowa nie jest tak prosta, to mogą się zdarzać ciekawe zjawiska.
Na przykład, stałe pole wektorowe
na torusie ![]() może mieć gęste krzywe fazowe, tj. gdy
może mieć gęste krzywe fazowe, tj. gdy ![]() jest niewymierne. Wtedy krzywe fazowe są obmotkami
(jak na Rysunku 4.1 powyżej) a ruch jest prawie okresowy, co
oznacza, że rozwiązanie powraca z grubsza okresowo do każdego małego obszaru przestrzeni fazowej. Ponadto, z każdego małego
obszaru można dojść do dowolnego innego małego obszaru. Taka własność nazywa się tranzytywnością w teorii Układów Dynamicznych. Ruch nie jest w pełni deterministyczny, dlatego
że po długim czasie trudno powiedzieć, gdzie znajduje się
ewoluująca cząstka. Jednak nie jest to ruch chaotyczny, ponieważ, jeśli na początku mieliśmy skupiony obszar przestrzeni
fazowej, to ten obszar zachowuje swój skupiony kształt w trakcie
ewolucji. Tymczasem w ruchu chaotycznym taka komórka zaczyna
`rozpływać się' w przestrzeni fazowej.
jest niewymierne. Wtedy krzywe fazowe są obmotkami
(jak na Rysunku 4.1 powyżej) a ruch jest prawie okresowy, co
oznacza, że rozwiązanie powraca z grubsza okresowo do każdego małego obszaru przestrzeni fazowej. Ponadto, z każdego małego
obszaru można dojść do dowolnego innego małego obszaru. Taka własność nazywa się tranzytywnością w teorii Układów Dynamicznych. Ruch nie jest w pełni deterministyczny, dlatego
że po długim czasie trudno powiedzieć, gdzie znajduje się
ewoluująca cząstka. Jednak nie jest to ruch chaotyczny, ponieważ, jeśli na początku mieliśmy skupiony obszar przestrzeni
fazowej, to ten obszar zachowuje swój skupiony kształt w trakcie
ewolucji. Tymczasem w ruchu chaotycznym taka komórka zaczyna
`rozpływać się' w przestrzeni fazowej.
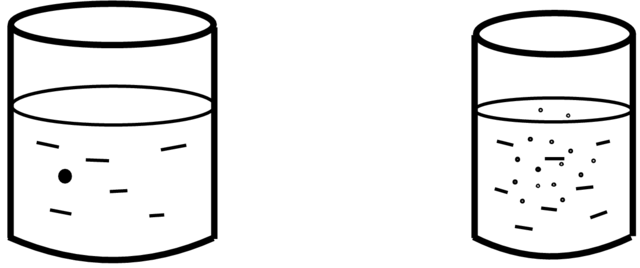
Przykład 5.1 (Tranzytywność i chaos). Dobrym przykładem sytuacji obrazującej różnicę pomiędzy tranzytywnością a chaosem są dwie szklanki z wodą takie, że w jedną wpuszczono małą kropelkę oliwy a w drugą wlano taką samą ilość soku (Rysunek 5.1). Kropelka oliwy będzie dryfować, odwiedzająć każde miejsce w wodzie, a sok zacznie się rozpuszczać, zapełniając równomiernie cały obszar wody (ta własność jest też nazywana mieszaniem).
Chyba najprostszymi układami różniczkowymi, w których można zaobserwować chaos są okresowe nieautonomiczne układy postaci
| (5.1) |
gdzie ![]() jest
jest ![]() wymiarową rozmaitością. Jak wiemy, taki układ można potraktować jako autonomiczny w rozszerzonej przestrzeni
fazowej
wymiarową rozmaitością. Jak wiemy, taki układ można potraktować jako autonomiczny w rozszerzonej przestrzeni
fazowej ![]() Wtedy wygodnie jest pracować z przekształceniem monodromi (po okresie)
Wtedy wygodnie jest pracować z przekształceniem monodromi (po okresie)
gdzie ![]() jest
jest ![]() parametrową rodziną dyfeomorfizmów
definiujących ewolucję. W terminach rozszerzonej przestrzeni
fazowej jest to przekształcenie powrotu na hiperpowierzchnię
parametrową rodziną dyfeomorfizmów
definiujących ewolucję. W terminach rozszerzonej przestrzeni
fazowej jest to przekształcenie powrotu na hiperpowierzchnię ![]()
W monografii J. Guckenheimera i P. Holmes'a [11] jest zanalizowany przykład układu Duffinga z siłą zewnętrzną
My zajmiemy się nieco innym przykładem.
Przykład 5.2 (Huśtawka). Jest to równanie
gdzie ![]() jest małą okresową siłą zewnętrzną, z okresem
jest małą okresową siłą zewnętrzną, z okresem ![]() . Można
to interpretować jak równanie huśtawki z dziewczynką, która wykonuje okresowe przykucnięcia (patrz Rysunek 5.2). Można też potraktować ten układ jako podukład
. Można
to interpretować jak równanie huśtawki z dziewczynką, która wykonuje okresowe przykucnięcia (patrz Rysunek 5.2). Można też potraktować ten układ jako podukład ![]() wymiarowego układu
autonomicznego
wymiarowego układu
autonomicznego
Skupmy się jednak na rozszerzonej przestrzeni fazowej ![]() gdzie
gdzie ![]() jest cylindrem i
mamy
jest cylindrem i
mamy
| (5.2) |
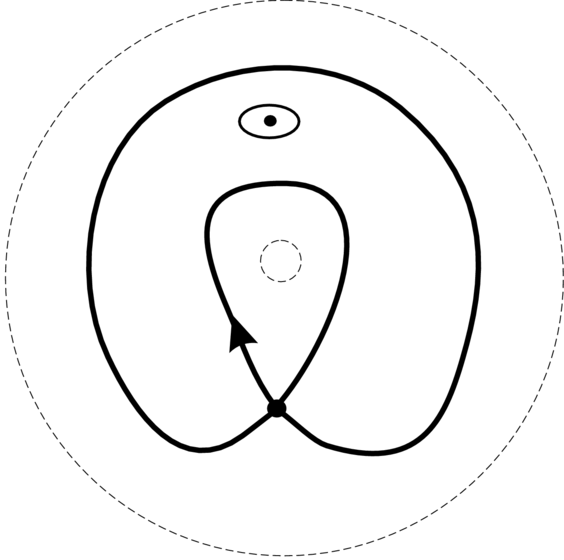
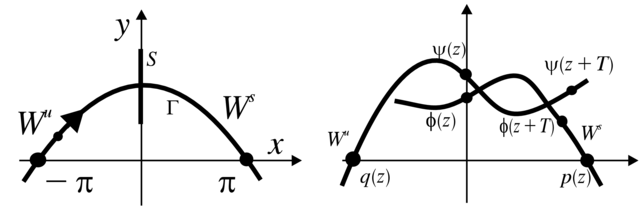
Dla sytuacji niezaburzonej (![]() ) portret fazowy jest znany
(patrz Rysunek 2.1 powyżej); my go przedstawiamy na Rysunku 5.3, gdzie górna i dolna krawędzie walca są przedstawione jako koncentryczne
przerywane okręgi. Nas interesuje, co będzie się działo z pętlą separatrys
) portret fazowy jest znany
(patrz Rysunek 2.1 powyżej); my go przedstawiamy na Rysunku 5.3, gdzie górna i dolna krawędzie walca są przedstawione jako koncentryczne
przerywane okręgi. Nas interesuje, co będzie się działo z pętlą separatrys ![]() punktu siodłowego
punktu siodłowego ![]()
![]()
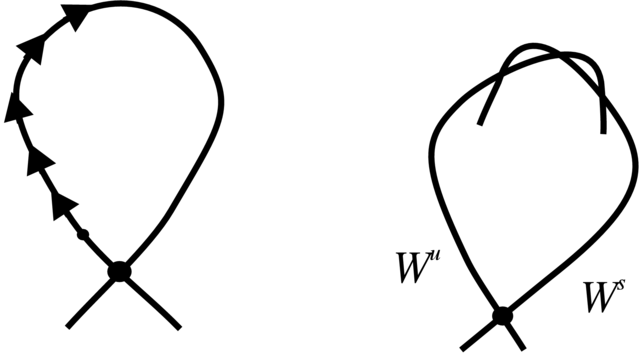
Gdyby zaburzenie było niezależne od czasu, to oczekiwany portret fazowy zaburzonego pola byłby jak na Rysunku 5.4, czyli separatrysy punktu siodłowego rozdzieliłyby się. Jednak w przypadku układu nieautonomicznym, ale okresowym ze względu na czas, portret fazowy układu niezaburzonego należy traktować jako dynamikę przekształcenia monodromii. Przy tym w układzie zaburzonym separatrysy nie mają obowiązku rozłączyć się. Spodziewamy się, że będą one przecinać się transwersalnie, jak na Rysunku 5.5. Niżej to wykażemy.
Rozwiązanie układu niezaburzonego, odpowiadające górnej pętli separatrys, jest następujące
| (5.3) |
(porównaj Zadanie 2.44). Ma ono tę własność, że ![]()
![]() i wartość całki pierwszej
i wartość całki pierwszej
| (5.4) |
wynosi ![]() (patrz Rysunek 5.6).
(patrz Rysunek 5.6).
Do badania ukladu zaburzonego (![]() ) użyjemy całej
rodziny przekształceń monodromii
) użyjemy całej
rodziny przekształceń monodromii
gdzie ![]() jest utożsamiane z cięciem
jest utożsamiane z cięciem ![]() w rozszerzonej przestrzeni fazowej
w rozszerzonej przestrzeni fazowej ![]() . Każde przekształcenie
. Każde przekształcenie ![]() ma swój punkt stały
ma swój punkt stały ![]() (utożsamiany z
(utożsamiany z ![]() ten punkt zależy od
ten punkt zależy od ![]() i od
i od ![]() i leży blisko punktu
i leży blisko punktu ![]()
![]() Ponieważ jest to punkt stały
i hiperboliczny (siodło) to ma swoją podrozmaitość stabilną
Ponieważ jest to punkt stały
i hiperboliczny (siodło) to ma swoją podrozmaitość stabilną
![]() i niestabilną
i niestabilną ![]() (patrz Rysunek 5.6); oczywiście te podrozmaitości też zależą od
(patrz Rysunek 5.6); oczywiście te podrozmaitości też zależą od ![]() i
i ![]() .
.
Wybierzmy cięcie ![]() transwersalne do
transwersalne do ![]() i do
i do ![]() . Niech
. Niech ![]() (odpowiednio
(odpowiednio ![]() będzie rozwiązaniem z warunkiem początkowym
będzie rozwiązaniem z warunkiem początkowym ![]() (odpowiednio
(odpowiednio ![]() Oczywiście
Oczywiście ![]() przy
przy ![]() i
i ![]() przy
przy ![]() Ponadto
Ponadto ![]() i
i ![]() (niezmienniczość podrozmaitości).
(niezmienniczość podrozmaitości).
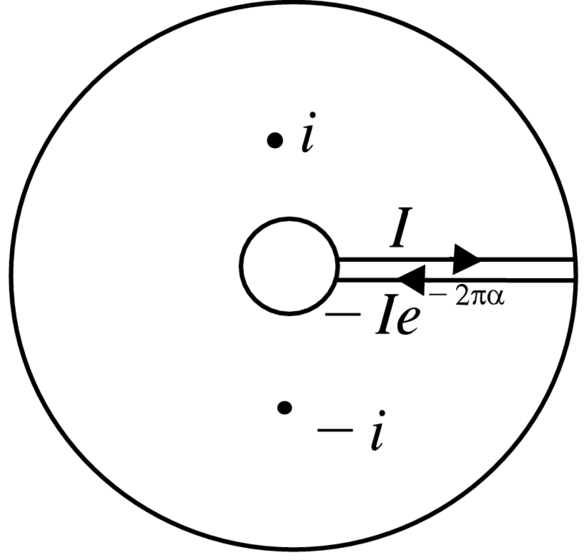
Punkt przecięcia podrozmaitości stabilnej i niestabilnej odpowiada
sytuacji, gdy ![]() dla odpowiedniego
dla odpowiedniego ![]() Jak w przypadu
autonomicznych zaburzeń układów hamiltonowskich (patrz Przykład
4.5) odległość pomiędzy
Jak w przypadu
autonomicznych zaburzeń układów hamiltonowskich (patrz Przykład
4.5) odległość pomiędzy ![]() i
i ![]() liczymy za
pomocą różnicy wartości całki pierwszej w tych punktach,
liczymy za
pomocą różnicy wartości całki pierwszej w tych punktach,
Mamy
![\begin{array}[]{lll}H(\psi(z)-H(q(z))&=&\int _{{-\infty}}^{{z}}\dot{H}dt=\varepsilon\int _{{-\infty}}^{{z}}y\cos\left(\omega t\right)dt,\\
H(p(z))-H(\phi(z))&=&\int _{{z}}^{{\infty}}\dot{H}dt=\varepsilon\int _{{z}}^{{\infty}}y\cos\left(\omega t\right)dt.\end{array}](wyklady/rrj/mi/mi1879.png) |
Zatem ![]() którą to całkę przybliżmy kładąc
którą to całkę przybliżmy kładąc ![]() ze wzoru (5.3). Dostajemy tzw. całkę Mielnikowa
(analog całki abelowej)
ze wzoru (5.3). Dostajemy tzw. całkę Mielnikowa
(analog całki abelowej)
| (5.5) |
Nietrudno pokazać następujący
Lemat 5.3.Jeśli ![]() i
i ![]() to podrozmaitości
to podrozmaitości ![]() i
i ![]() przecinają się transwersalnie w
punkcie bliskim
przecinają się transwersalnie w
punkcie bliskim![]() (Zadanie 5.5).
(Zadanie 5.5).
Okazuje się, że całka Mielnikowa ze wzoru (5.5) jest policzalna.
Podstawiając ![]() (z
(z ![]() ) dostajemy
) dostajemy
Wyliczymy całkę ![]() metodą konturową. Całka wzdłuż konturu z
Rysunku 5.7, w granicy z promieniami okręgów dążących do
metodą konturową. Całka wzdłuż konturu z
Rysunku 5.7, w granicy z promieniami okręgów dążących do
![]() i
i ![]() odpowiednio, wynosi
odpowiednio, wynosi
To daje ![]() i
i
Łatwo widać, że ta funkcja spełnia wymaganie ![]()
Znaleźliśmy przynajmniej jeden punkt ![]() przecięcia się
rozmaitości stabilnej i niestabilnej punktu stałego
przecięcia się
rozmaitości stabilnej i niestabilnej punktu stałego ![]() dla
dyfeomorfizmu
dla
dyfeomorfizmu
gdzie ![]() jest pewnym otoczeniem pętli separatrys
jest pewnym otoczeniem pętli separatrys ![]() siodła
siodła ![]()
![]() a
a ![]() jest wyróżnionym przekształceniem monodromii z rodzimy
jest wyróżnionym przekształceniem monodromii z rodzimy ![]() (z
hiperbolicznymi punktami stałymi
(z
hiperbolicznymi punktami stałymi ![]() . Ale takich punktów jest
znacznie więcej; są one postaci
. Ale takich punktów jest
znacznie więcej; są one postaci ![]()
![]() Przy
Przy ![]() i przy
i przy ![]() punkty
punkty ![]() dążą do punktu stałego
dążą do punktu stałego ![]()
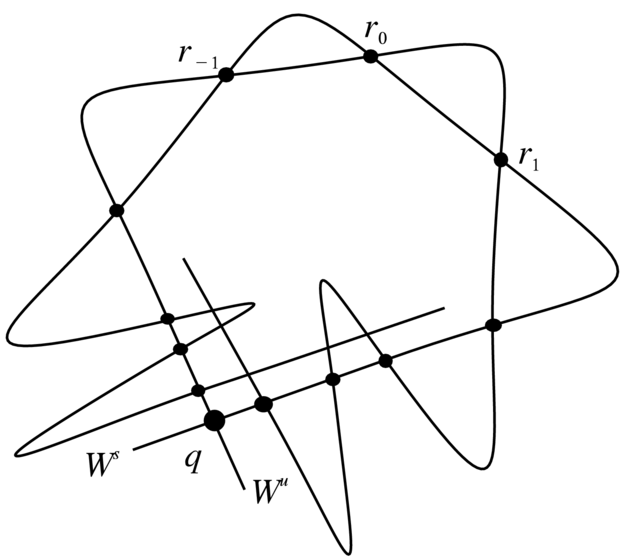
Jednakże podrozmaitości ![]() i
i ![]() zachowują się co najmniej niestandardowo. Na przykład, rozmaitość
zachowują się co najmniej niestandardowo. Na przykład, rozmaitość ![]() przechodząc przez coraz dalsze punkty
przechodząc przez coraz dalsze punkty ![]() zaczyna być coraz bardziej równoległa do
samej siebie, ale w okolicy siodła
zaczyna być coraz bardziej równoległa do
samej siebie, ale w okolicy siodła ![]() (czyli do lokalnej rozmaitości
niestabilnej
(czyli do lokalnej rozmaitości
niestabilnej ![]() Przy tym oczywiście, pomiędzy punktami
Przy tym oczywiście, pomiędzy punktami ![]() i
i ![]() wykonuje ostry zakręt. To samo mniej więcej
dzieje się z rozmaitością
wykonuje ostry zakręt. To samo mniej więcej
dzieje się z rozmaitością ![]() przyprzejściu
przez punkty
przyprzejściu
przez punkty ![]() dla
dla ![]() i pomiędzy tymi
punktami. W szczególności wyróżnione powyżej kawałki
i pomiędzy tymi
punktami. W szczególności wyróżnione powyżej kawałki ![]() i
i ![]() zaczynają się przecinać w innych puktach (niż
zaczynają się przecinać w innych puktach (niż ![]() Aż strach pomyśleć, co się dzieje przy
dalszych iteracjach; np. kawałki
Aż strach pomyśleć, co się dzieje przy
dalszych iteracjach; np. kawałki ![]() równoległe do
równoległe do ![]() zaczynają być coraz dłuższe (patrz Rysunek 5.8).
zaczynają być coraz dłuższe (patrz Rysunek 5.8).
ZADANIA
Zadanie 5.4. Pokazać, że jeśli ![]() jest
jest ![]() parametrową rodziną dyfeomorfizmów definiujących ewolucję
nieautonomicznego pola wektorowego
parametrową rodziną dyfeomorfizmów definiujących ewolucję
nieautonomicznego pola wektorowego ![]() które jest okresowe
z okresem
które jest okresowe
z okresem ![]() względem czasu, to
względem czasu, to ![]()
Zadanie 5.5. Udowodnić Lemat 5.3.
Wskazówka: Po pierwsze, pokazać, że (jako bliskie krzywej
fazowej z równania (5.3)) w otoczeniu punktu ![]()
![]() podrozmaitości
podrozmaitości ![]() i
i ![]() leżą poziomo, czyli są
wykresami pewnych funkcji od
leżą poziomo, czyli są
wykresami pewnych funkcji od ![]() Dla
Dla ![]() będziemy trakować
je jako wykresy funkcji
będziemy trakować
je jako wykresy funkcji ![]() i
i ![]() odpowiednio z pewnego odcinka
odpowiednio z pewnego odcinka ![]() (na
osi
(na
osi ![]() ów) do cięcia
ów) do cięcia ![]() przy czym
przy czym ![]() jest parametryzowane przez
jest parametryzowane przez ![]() .
.
Po drugie. przekształcenia ![]() i
i ![]() są sprzężone,
są sprzężone, ![]() Wywnioskować stąd, że
Wywnioskować stąd, że ![]() i podobnie jest z
i podobnie jest z ![]() Przekształcenia
Przekształcenia ![]() są bliskie przekształceniom
są bliskie przekształceniom ![]() potoku fazowego niezaburzonego układu (5.2), które w otoczeniu punktu
potoku fazowego niezaburzonego układu (5.2), które w otoczeniu punktu ![]()
![]() jest z grubsza
`ruchem w prawo'. Stąd wynika, że przy zmianie
jest z grubsza
`ruchem w prawo'. Stąd wynika, że przy zmianie ![]() rozmaitości
rozmaitości
![]() powstają z rozmaitości
powstają z rozmaitości ![]() przez
`przesuwanie' jej. Stąd wynika, że jeśli
przez
`przesuwanie' jej. Stąd wynika, że jeśli ![]() jest zadane
jak w (5.3), to funkcję
jest zadane
jak w (5.3), to funkcję ![]() , której wykresem jest
, której wykresem jest ![]() można zadać w pierwszym przybliżeniu jako
można zadać w pierwszym przybliżeniu jako
Podobnie wykres funkcji ![]() w pierwszym przybliżeniu zadaje
w pierwszym przybliżeniu zadaje ![]() . Różnica
. Różnica ![]() . Pokazać, że
warunek transwersalności
. Pokazać, że
warunek transwersalności ![]() i
i ![]() wynika z własności:
wynika z własności: ![]() dla
dla ![]()
5.2. Podkowa Smale'a, dyfeomorfizmy Anosowa i atraktory
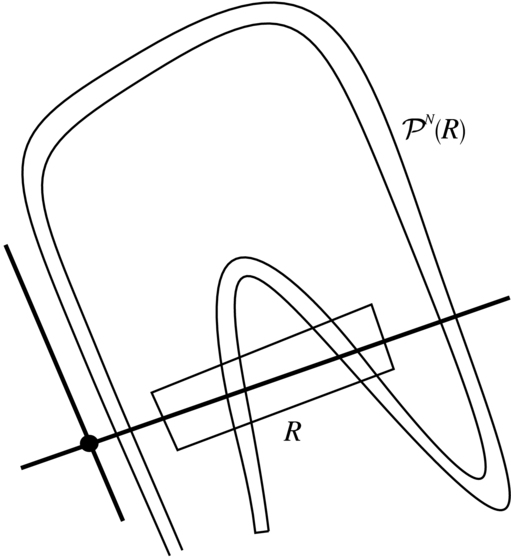
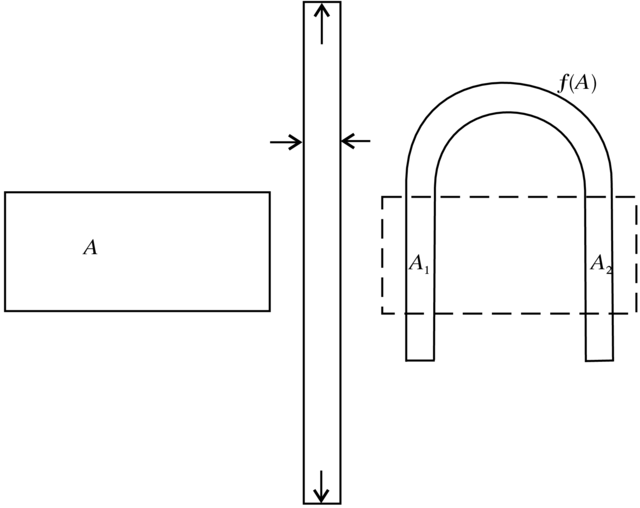
Prawdopodobnie S. Smale był pierwszym, który dobrze zrozumiał zjawisko z końca poprzedniego rozdziału i opisał je w ścisłych matematycznych terminach. Na Rysunku 5.9 widzimy (nieco krzywoliniowy)
`prostokąt ' ![]() wzdłuż lokalnej rozmaitości stabilnej
wzdłuż lokalnej rozmaitości stabilnej ![]() który pod działaniem odpowiednio wysokiej iteracji
przekształcenia
który pod działaniem odpowiednio wysokiej iteracji
przekształcenia ![]() przechodzi na figurę, która
przecina
przechodzi na figurę, która
przecina ![]() w dwu miejscach. Można dobrać parametry definiujące
prostokąt
w dwu miejscach. Można dobrać parametry definiujące
prostokąt ![]() , aby to rzeczywiście miało miejsce; (my tego nie
robimy, ale możemy odesłać czytelnika do książek R.
Devaney'a [9], C. Robinsona [17] i W. Szlenka [18]).
, aby to rzeczywiście miało miejsce; (my tego nie
robimy, ale możemy odesłać czytelnika do książek R.
Devaney'a [9], C. Robinsona [17] i W. Szlenka [18]).
Modelowy przykład przekształcenia jak na Rysunku 5.9 to przekształcenie podkowy Smale'a przedstawione na Rysunku 5.10.
Definicja 5.6 (Podkowa Smale'a). Mamy (autentyczny) prostokąt ![]() na płaszczyźnie
na płaszczyźnie![]() z którym dokonujemy następującej
operacji. Najpierw wydłużmy go w kierunku pionowym i zwężamy w
kierunku poziomym. Następnie zaginamy nasz wydłużony prostokąt
i kładziemy na płaszczyznę tak ,aby przecinał wyjściowy prostokąt wzdłuż dwóch równoległych pionowych pasków
z którym dokonujemy następującej
operacji. Najpierw wydłużmy go w kierunku pionowym i zwężamy w
kierunku poziomym. Następnie zaginamy nasz wydłużony prostokąt
i kładziemy na płaszczyznę tak ,aby przecinał wyjściowy prostokąt wzdłuż dwóch równoległych pionowych pasków
W ten sposób dostajemy nową figurę, oznaczaną ![]() gdzie
gdzie ![]() jest dyfeomorfizmem podkowy.18Można to przekształcenie przedłużyć. Doklejmy do dolnej i górnej podstaw
jest dyfeomorfizmem podkowy.18Można to przekształcenie przedłużyć. Doklejmy do dolnej i górnej podstaw ![]() półkola i oznaczmy nową figurę przez
półkola i oznaczmy nową figurę przez ![]() Przedłużmy
Przedłużmy ![]() na ba półkola, tak aby ich obrazy przylegały do
dolnych końców
na ba półkola, tak aby ich obrazy przylegały do
dolnych końców ![]() . Zakładając, że nowa figura leży
całkowicie w
. Zakładając, że nowa figura leży
całkowicie w ![]() , dostajemy dobrze określony dyfeomorfizm
, dostajemy dobrze określony dyfeomorfizm ![]()
Podkowa Smale'a, chociaż prosto zdefiniowana, wcale taka prosta nie
jest. Latwo stwierdzić, że ![]() składa się z 4
pionowych pasków; ogólniej,
składa się z 4
pionowych pasków; ogólniej, ![]() składa się z
składa się z ![]() pionowych pasków (Zadanie 5.14). Z drugiej strony,
pionowych pasków (Zadanie 5.14). Z drugiej strony, ![]() składa się z dwu poziomych pasków; ogólniej,
składa się z dwu poziomych pasków; ogólniej, ![]()
![]() składa się z
składa się z ![]() poziomych i
cienkich pasków (Zadanie 5.15). Zatem
poziomych i
cienkich pasków (Zadanie 5.15). Zatem ![]()
![]() składa się z
składa się z ![]() małych prostokącików.
Bardzo ważny jest następujący zbiór
małych prostokącików.
Bardzo ważny jest następujący zbiór
| (5.6) |
Łatwo sprawdzić, że jest to zbiór niezmienniczy względem ![]()
![]() (Zadanie 5.16). Można
powiedzieć więcej o
(Zadanie 5.16). Można
powiedzieć więcej o ![]() i o
i o ![]() ale najpierw
powinniśmy wprowadzić jedną definicję.
ale najpierw
powinniśmy wprowadzić jedną definicję.
Definicja 5.7. Niech ![]() będzie przeliczalnym iloczynem kartejańskim ustalonego zbioru
będzie przeliczalnym iloczynem kartejańskim ustalonego zbioru ![]() elementowego; składa się ona z ciągów
elementowego; składa się ona z ciągów ![]()
![]() . Zdefiniujemy przekształcenie
. Zdefiniujemy przekształcenie ![]() następująco:
następująco:
Układ dynamiczny ![]() zdefiniowany powyżej
nazywa się układem symbolicznym, albo przesunięciem.
zdefiniowany powyżej
nazywa się układem symbolicznym, albo przesunięciem.
Na przetrzeni ![]() wprowadza się topologię produktową,
gdzie otoczeniami danego ciągu symboli
wprowadza się topologię produktową,
gdzie otoczeniami danego ciągu symboli ![]() są zbiory cylindryczne
postaci
są zbiory cylindryczne
postaci
(dla ustalonych ![]()
![]() jest też przestrzenią metryczna,
bo odległość dwóch ciągów to
jest też przestrzenią metryczna,
bo odległość dwóch ciągów to ![]()
Ma miejsce następujące
Twierdzenie 5.8.Istnieje ciągły homeomorfizm ![]() który sprzęga
który sprzęga ![]() z
z![]()
Dowód. Przekształcenie ![]() jest łatwe do
zdefiniowania. Jeśli
jest łatwe do
zdefiniowania. Jeśli ![]() to kładziemy
to kładziemy ![]() gdzie
gdzie
Własność sprzęgania sprawdza się bezpośrednio (Zadanie
5.18). Pozostaje zatem tylko sprawdzić ciągłość i
odwracalność przekształcenia ![]()
Te dwie własności wynikają z hiperboliczności przekształcenia podkowy: w kierunku poziomym jest ściskanie ze stałą ![]() a w kierunku pionowym mamy rozciąganie ze stałą
a w kierunku pionowym mamy rozciąganie ze stałą ![]() Zatem prostokąciki, pojawiające się przy
lokalizacji punktów
Zatem prostokąciki, pojawiające się przy
lokalizacji punktów ![]() tzn.
tzn.
| (5.7) |
stają się eksponencjalnie małe przy ![]() i
i ![]() bardzo dużych. W
granicy dostaniemy tylko jeden punkt (odwracalność). Małe rozmiary
zbiorów (5.7) odpowiadają małości odpowiednich zbiorów
cylindrycznych w
bardzo dużych. W
granicy dostaniemy tylko jeden punkt (odwracalność). Małe rozmiary
zbiorów (5.7) odpowiadają małości odpowiednich zbiorów
cylindrycznych w ![]() jest to dokładnie ciągłość
jest to dokładnie ciągłość ![]() i
i ![]() ∎
∎
Ponieważ ![]() jest jedynym zbiorem niezmienniczym w prostokącie
jest jedynym zbiorem niezmienniczym w prostokącie ![]() to cała interesująca dynamika przekształcenia podkowy
ogranicza się do dynamiki
to cała interesująca dynamika przekształcenia podkowy
ogranicza się do dynamiki ![]() Dzięki powyższemu
twierdzeniu jest to taka sama dynamika, jak dla przekształcenia
symbolicznego
Dzięki powyższemu
twierdzeniu jest to taka sama dynamika, jak dla przekształcenia
symbolicznego ![]() na
na ![]() Z drugiej strony, przekształcenie
symboliczne jest przyjemne do badania. Ma ono następujące ciekawe włsności.
Z drugiej strony, przekształcenie
symboliczne jest przyjemne do badania. Ma ono następujące ciekawe włsności.
Stwierdzenie 5.9.Punkty okreowe dla ![]() są gęste w przestrzeni symbolicznej
są gęste w przestrzeni symbolicznej![]()
Dowód. Niech ![]() . Dla dużego
. Dla dużego ![]() wszyskie ciągi
wszyskie ciągi![]() takie, że
takie, że ![]() są bliskie
są bliskie ![]() Zatem bliski jest też ciąg utworzony z bloku
Zatem bliski jest też ciąg utworzony z bloku ![]() (długości
(długości ![]() i powtarzanego periodycznie. Odpowiada on puktowi
okresowemu dla
i powtarzanego periodycznie. Odpowiada on puktowi
okresowemu dla ![]() o okresie
o okresie ![]() . ∎
. ∎
Stwierdzenie 5.10.Układ dynamiczny ![]() jest tranzytywny, tzn. dla dowolnych podzbiorów otwartych
jest tranzytywny, tzn. dla dowolnych podzbiorów otwartych ![]() istnieje i
istnieje i ![]() takie, że
takie, że![]()
Dowód. Wystarczy rozważyć przypadek, gdy ![]() i
i ![]() są zbiorami cylindrycznymi definiowanymi przy pomocy bloków
są zbiorami cylindrycznymi definiowanymi przy pomocy bloków ![]() i
i ![]() Wtedy
wystaczy wziąć dowolny ciąg z blokiem
Wtedy
wystaczy wziąć dowolny ciąg z blokiem ![]() (długości
(długości ![]() ∎
∎
Uwaga 5.11. Można wprowadzić na ![]() probabilistyczną miarę produktową
probabilistyczną miarę produktową ![]() , taką, że
, taką, że ![]() (miara Bernoulliego). Okazuje się ona być niezmiennicza względem przesunięcia
(miara Bernoulliego). Okazuje się ona być niezmiennicza względem przesunięcia ![]() Ponadto
zachodzi własność mieszania, o której wspomniałem na początku rozdziału a której nie chcę ściśle definiować. Zatem układ podkowy Smale'a a także układ huśtawki są układami chaotycznymi.
Ponadto
zachodzi własność mieszania, o której wspomniałem na początku rozdziału a której nie chcę ściśle definiować. Zatem układ podkowy Smale'a a także układ huśtawki są układami chaotycznymi.
Podzbiór ![]() niezmienniczy dla przekształcenia podkowy Smale's, ma jeszcze jedną ważną własność. Mianowicie jest hiperboliczny, co oznacza, że indukowane
przekształcenia liniowe
niezmienniczy dla przekształcenia podkowy Smale's, ma jeszcze jedną ważną własność. Mianowicie jest hiperboliczny, co oznacza, że indukowane
przekształcenia liniowe ![]() są hiperboliczne (mają jedną wartość własną
są hiperboliczne (mają jedną wartość własną ![]() i drugą
i drugą ![]()
Niestety, zbiór ![]() jest bardzo cienki (jego wymiar Hausdorffa
zależy od
jest bardzo cienki (jego wymiar Hausdorffa
zależy od ![]() i
i ![]() i na pewno nie jest rozmaitością (nawet lokalnie). Ale istnieją chaotyczne układy
dynamiczne ze strukturą hiperboliczną na całej rozmaitości. Są to tzw. dyfeomorfizmy Anosowa, których najbardziej znanym
reprezentatnem jest następujący
i na pewno nie jest rozmaitością (nawet lokalnie). Ale istnieją chaotyczne układy
dynamiczne ze strukturą hiperboliczną na całej rozmaitości. Są to tzw. dyfeomorfizmy Anosowa, których najbardziej znanym
reprezentatnem jest następujący
Przykład 5.12 (Hiperboliczny automorfizm torusa). Utożsamijmy
dwuwymiatowy torus z płaszczyzną podzieloną przez kratę, ![]() Macierz
Macierz
zadaje przekształcenie płaszczyzny, które punkty o współrzędnych całkowitych przekształca na podobne punkty. Zatem definiuje ono
przekształcenie ![]() Ponieważ
wyznacznik naszej macierzy jest równy 1, to i przekształcenie odwrotne
zachowuje kratę; zatem
Ponieważ
wyznacznik naszej macierzy jest równy 1, to i przekształcenie odwrotne
zachowuje kratę; zatem ![]() jest dyfeomorfizmem.
jest dyfeomorfizmem.
Przekształcenie ![]() ma dokładnie jeden punkt stały, odpowiadający
punktowi
ma dokładnie jeden punkt stały, odpowiadający
punktowi ![]() Za to równania na punkty okresowe o
okresie 2 przyjmują postać
Za to równania na punkty okresowe o
okresie 2 przyjmują postać ![]()
![]()
![]() Nietrudno zobaczyć, że daje to 25 rozwiązań. Ogólnie, ze wzrostem
Nietrudno zobaczyć, że daje to 25 rozwiązań. Ogólnie, ze wzrostem ![]() liczba punktów okresowych dla
liczba punktów okresowych dla ![]() o okresie
o okresie ![]() rośnie do nieskończoności; w szczególności, punkty z wymiernymi obiema współrzędnymi są okresowe (Zadanie 5.19).
rośnie do nieskończoności; w szczególności, punkty z wymiernymi obiema współrzędnymi są okresowe (Zadanie 5.19).
Macierz pochodnej ![]() w każdym punkcie
w każdym punkcie ![]() jest taka sama i równa
jest taka sama i równa ![]() Z
kolei macierz
Z
kolei macierz ![]() jest hiperboliczna, z wartościami własnymi
jest hiperboliczna, z wartościami własnymi ![]() i
i ![]() Zatem
Zatem ![]() ma (równomierną) strukturę hiperboliczną. (Ta własność wchodzi w definicję dyfeomorfizmu Anosowa, której nie przytaczam).
ma (równomierną) strukturę hiperboliczną. (Ta własność wchodzi w definicję dyfeomorfizmu Anosowa, której nie przytaczam).
Co więcej, przez każdy punkt ![]() przechodzą
dwie specjalne krzywe: jedna
przechodzą
dwie specjalne krzywe: jedna ![]() odpowiada prostej w kierunku własnym odpowiadającym
odpowiada prostej w kierunku własnym odpowiadającym ![]() i druga
i druga ![]() odpowieda
prostej w drugim kierunku własnym. Ponieważ wartości własne są niewymierne, to współczynniki nachylenia obu kierunków własnych są niewymierne. Zatem każda z rozmaitości
odpowieda
prostej w drugim kierunku własnym. Ponieważ wartości własne są niewymierne, to współczynniki nachylenia obu kierunków własnych są niewymierne. Zatem każda z rozmaitości ![]() i
i ![]() jest gęsta w torusie (tworzy obmotkę); w topologii mówi się o podrozmaitościach immersyjnych.
jest gęsta w torusie (tworzy obmotkę); w topologii mówi się o podrozmaitościach immersyjnych.
Okazuje się, że hiperboliczny automorfizm torusa ma własność tranzytywności mieszania względem miary Lebesque'a (która jest zachowana przez ![]()
Na koniec, poinformuję czytelników, że dyfeomorfizm ![]() jest
strukturalnie stabilny. To znaczy, że dowolny bliski niemu dyfeomorfizm
jest
strukturalnie stabilny. To znaczy, że dowolny bliski niemu dyfeomorfizm ![]() jest z nim sprzężony przy pomocy pewnego homeomorfizmu torusa
jest z nim sprzężony przy pomocy pewnego homeomorfizmu torusa ![]() (analog Twierdzenia Grobmana–Hartmana). Jest to ogólna własność dyfeomorfizmów Anosowa.
(analog Twierdzenia Grobmana–Hartmana). Jest to ogólna własność dyfeomorfizmów Anosowa.
Innym naturalny układem typu Anosowa jest potok geodezyjny na powierzchni o stałej ujemnej krzywiźnie.
Bardzo ważnymi przykładami układów dynamicznych są tzw.
atraktory hiperboliczne. Są to przekształcenia gładkie
(nawet niekoniecznie odwracalne) ![]() dla których istnieje
domknięty podzbiór niezmienniczy
dla których istnieje
domknięty podzbiór niezmienniczy ![]() z otoczeniem
z otoczeniem ![]() takim, że
takim, że ![]() Lokalnie
Lokalnie ![]() ma postać
ma postać ![]() gdzie
gdzie ![]() jest regularną
rozmaitością (z
jest regularną
rozmaitością (z ![]() a
a ![]() jest zbiorem typu Cantora.
jest zbiorem typu Cantora.
Ponadto ![]() ma strukturę hiperboliczną w tym sensie, że
ma strukturę hiperboliczną w tym sensie, że ![]() jednostajnie rozciąga w kierunku
jednostajnie rozciąga w kierunku ![]() i jednostajnie
ściska w kierunku transwersalnym do
i jednostajnie
ściska w kierunku transwersalnym do ![]()
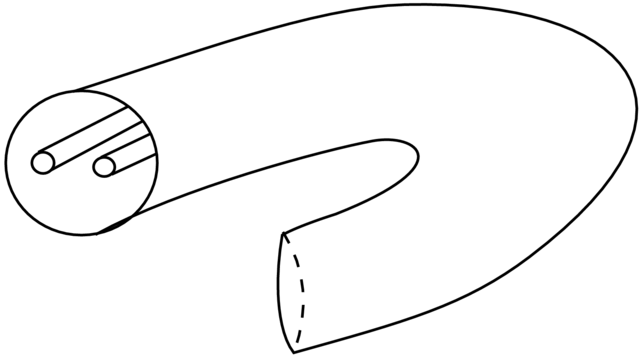
Przykład 5.13 (Selenoid). Niech ![]() będzie pełnym torusem, gdzie
będzie pełnym torusem, gdzie
![]() to dysk a
to dysk a ![]() . Przekształcenie jest zadane następująco
. Przekształcenie jest zadane następująco
Obrazem ![]() będzie torus czterokrotnie cieńczy i
dwukrotnie dłuższy oraz włożony w
będzie torus czterokrotnie cieńczy i
dwukrotnie dłuższy oraz włożony w ![]() tak, że owija się
dwukrotnie wokół `równika'
tak, że owija się
dwukrotnie wokół `równika' ![]() przy tym lekko skręcając
(patrz Rysunek 5.11).
przy tym lekko skręcając
(patrz Rysunek 5.11).
Oczywiście ![]() jest zbiorem
niezmienniczym i spełnia wymagania, które nałożyłem powyżej na hiperboliczne atraktory.
jest zbiorem
niezmienniczym i spełnia wymagania, które nałożyłem powyżej na hiperboliczne atraktory.
Na koniec, chciałbym zauważyć, że w teorii układów
dynamicznych trudny do rozwiązania problem stanowią tzw. dziwne atraktory, które spełniają własność ![]() ale nie chcą być równomiernie
hiperboliczne. Najbardziej znane to atraktor Hènona zadany
odwzorowaniem
ale nie chcą być równomiernie
hiperboliczne. Najbardziej znane to atraktor Hènona zadany
odwzorowaniem
(gdzie np. ![]() i
i ![]() i atraktor Lorenza zadany polem
wektorowym
i atraktor Lorenza zadany polem
wektorowym
(gdzie np. ![]()
![]() i
i ![]()
ZADANIA
Zadanie 5.14. Narysować ![]()
Zadanie 5.15. Pokazać, że ![]()
![]() składa się z
składa się z ![]() poziomych pasków.
poziomych pasków.
Zadanie 5.16. Udowodnić, że ![]() ze wzoru (5.6) jest
zbiorem niezmienniczym.
ze wzoru (5.6) jest
zbiorem niezmienniczym.
Zadanie 5.17. Pokazać, że ![]() (z (5.6)) jest
homeomorficzne z
(z (5.6)) jest
homeomorficzne z ![]() gdzie
gdzie ![]() jest (odpowiednio zdefiniowanym)
zbiorem Cantora.
jest (odpowiednio zdefiniowanym)
zbiorem Cantora.
Zadanie 5.18. Sprawdzić, że ![]() sprzęga
sprzęga ![]() z
z ![]()
Zadanie 5.19. Udowodnić, że zbiór punktów okresowych przekształcenia z Przykładu 5.12 pokrywa się ze zbiorem punktów o wymierych obu współrzędnych.
Wskazówka: Zbiór ![]() dla ustalonego
dla ustalonego ![]() jest skończony i niezmienniczy względem
jest skończony i niezmienniczy względem ![]() Ponadto równania na punkty okresowy o okresie
Ponadto równania na punkty okresowy o okresie ![]() przyjmują
postać
przyjmują
postać ![]() gdzie
gdzie ![]()