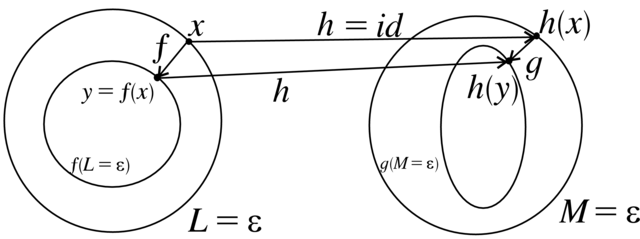1. Punkty równowagi pól wektorowych
Rozważmy nieautonomiczny układ równań różniczkowych (lub pole wektorowe zależne od czasu)
| (1.1) |
Tutaj ![]() należy do pewnej rozmaitości
należy do pewnej rozmaitości ![]() zaś
zaś ![]() (czas) do
przedziału
(czas) do
przedziału ![]() . W tym rozdziale możemy zakładać, że
. W tym rozdziale możemy zakładać, że ![]() jest otwartym podzbiorem
jest otwartym podzbiorem ![]() i że pole
i że pole ![]() jest klasy
jest klasy ![]()
![]() tak, że spełnione są założenia twierdzeń z Dodatku.
tak, że spełnione są założenia twierdzeń z Dodatku.
Przypomnijmy, że punkt ![]() taki, że
taki, że
(dla każdego ![]() nazywa się punktem równowagi; inne
nazwy spotykane w literaturze to: punkt osobliwy pola i punkt krytyczny pola (głównie w przypadku pola autonomicznego). Oczywiście
nazywa się punktem równowagi; inne
nazwy spotykane w literaturze to: punkt osobliwy pola i punkt krytyczny pola (głównie w przypadku pola autonomicznego). Oczywiście ![]() jest rozwiązaniem tego układu. Celem tego rozdziału jest zbadanie własności rozwiązań
układu (1.1) w otoczeniu pnktu równowagi.
jest rozwiązaniem tego układu. Celem tego rozdziału jest zbadanie własności rozwiązań
układu (1.1) w otoczeniu pnktu równowagi.
1.1. Stabilność w sensie Lapunowa i asymptotyczna stabilność
Najprostszą i pożądaną z punktu widzenia zastosowań własnością puktu równowagi jest jego stabilność. Poniżej podajemy dwie matematycznie ścisłe definicje stabilności.
Definicja 1.1. Punkt równowagi ![]() równania (1.1)
jest stabily w sensie Lapunowa, jeśli dla każdego
równania (1.1)
jest stabily w sensie Lapunowa, jeśli dla każdego ![]() istnieje
istnieje ![]() takie, że każde rozwiązanie
takie, że każde rozwiązanie ![]() startujące z
startujące z ![]() otoczenia
puktu
otoczenia
puktu ![]() ,
, ![]() pozostaje w
pozostaje w ![]() otoczeniu tego punktu,
otoczeniu tego punktu, ![]() dla wszystkich czasów
dla wszystkich czasów ![]()
Punkt równowagi ![]() jest asymptotycznie stabilny, jeśli jest on stabilny w sensie Lapunowa i, dodatkowo, istnieje
jest asymptotycznie stabilny, jeśli jest on stabilny w sensie Lapunowa i, dodatkowo, istnieje ![]() takie, że każde rozwiązanie
takie, że każde rozwiązanie ![]() startujące z punktu
startujące z punktu ![]()
![]() bliskiego punktowi równowagi,
bliskiego punktowi równowagi, ![]() , dąży do
, dąży do ![]() przy
przy ![]()
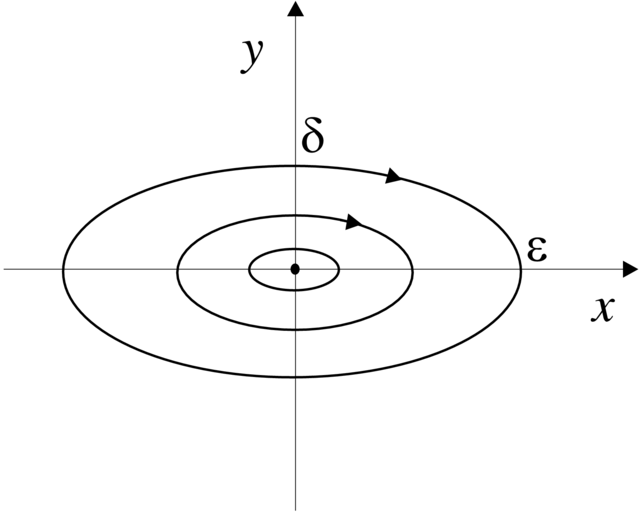
Przykład 1.2. Dla oscylatora harmonicznego ![]() albo
albo
rozwiązania leżą w elipsach ![]() (patrz Rysunek 1.1). Stąd dla
(patrz Rysunek 1.1). Stąd dla ![]() wynika, że wybór
wynika, że wybór ![]() spełnia warunki definicji stabilności w sensie Lapunowa. Ponieważ
rozwiązania nie dążą do punktu równowagi
spełnia warunki definicji stabilności w sensie Lapunowa. Ponieważ
rozwiązania nie dążą do punktu równowagi ![]() nie
jest on asymptotycznie stabilny.
nie
jest on asymptotycznie stabilny.
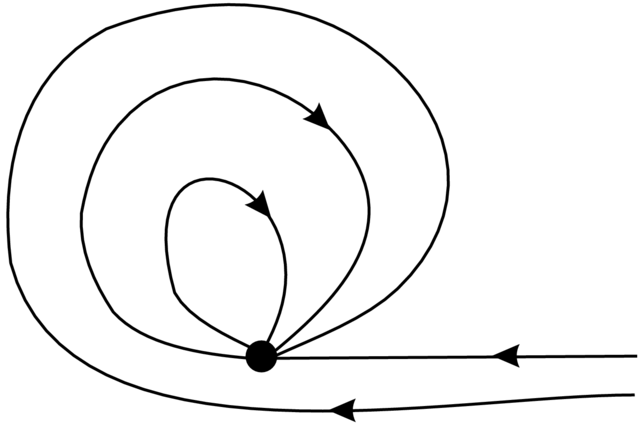
Przykład 1.3. Na Rysunku 1.2 przedstawiono portret fazowy pewnego pola wektorowego, które ma tę własność, że każde rozwiązanie dąży do punktu równowagi (czyli jest spełniony drugi z warunków na stabilność asymptotyczną). Jednakowoż ten punkt równowagi nie jest stabily w sensie Lapunowa, ponieważ trajektorie starujące z dołu oraz dowolnie blisko punktu równowagi wychodzą z czasem z ustalonego otoczenia tego punktu.
Okazuje się, że odpowiednie autonomiczne pole wektorowe można zadać konkretnym wzorem. Mianowicie, ma ono postać
| (1.2) |
(patrz Zadanie 2.64).
Podstawowy wynik o stabilności punktów równowagi pochodzi od A.
Lapunowa. Dotyczy ono punktu równowagi ![]() dla kiełka1Przez kiełek pola wektorowego
dla kiełka1Przez kiełek pola wektorowego ![]() (lub funkcji
(lub funkcji ![]() czy formy różniczkowej
czy formy różniczkowej ![]() czy odwzorowania) w punkcie
czy odwzorowania) w punkcie ![]() rozumiemy pole wektorowe (lub funkcję lub formę różniczkową lub odwzorowanie) określoną na pewnym otoczeniu
rozumiemy pole wektorowe (lub funkcję lub formę różniczkową lub odwzorowanie) określoną na pewnym otoczeniu ![]() punktu
punktu ![]() Dwa kiełki, jeden określony na otoczeniu
Dwa kiełki, jeden określony na otoczeniu ![]() a drugi
na
a drugi
na ![]() są równoważne, jeśli są zgodne na
pewnym otoczeniu
są równoważne, jeśli są zgodne na
pewnym otoczeniu ![]() Przyjmuje się oznaczenie
Przyjmuje się oznaczenie ![]() dla oznaczenia
kiełka funkcji w
dla oznaczenia
kiełka funkcji w ![]() analogoczne oznaczenia są dla pól
wektorowych, form różniczkowych, odwzorowań, itd.
autonomicznego pola wetorowego w
analogoczne oznaczenia są dla pól
wektorowych, form różniczkowych, odwzorowań, itd.
autonomicznego pola wetorowego w ![]() postaci
postaci
| (1.3) |
gdzie ![]() jest macierzą linearyzacji
pola w punkcie
jest macierzą linearyzacji
pola w punkcie ![]()
Twierdzenie 1.4 (Lapunow). Jeśli macierz ![]() ma własność, że części rzeczywiste wszystkich jej wartości własnych są ujemne,
ma własność, że części rzeczywiste wszystkich jej wartości własnych są ujemne,
| (1.4) |
to punkt równowagi ![]() jest asymptotycznie stabilny.
jest asymptotycznie stabilny.
Zanim zaczniemy ścisły dowód tego twierdzenia wprowadzimy pojęcie funkcji Lapunowa, które okazuje się być użyteczne dla pokazywania asymptotycznej stabilności nawet bez założenia (1.4).
Definicja 1.5.Funkcją Lapunowa dla punktu równowagi ![]() kiełka autonomicznego pola wektorowego
kiełka autonomicznego pola wektorowego ![]() nazywamy
funkcję
nazywamy
funkcję
z otoczenia ![]() punktu
punktu ![]() która spełnia następujące dwie
własności:
która spełnia następujące dwie
własności:
(i) ![]() i
i ![]() tylko dla
tylko dla ![]()
(ii) ![]() dla
dla ![]()
Stwierdzenie 1.6. Jeśli istnieje funkcja Lapunowa (dla
punktu równowa- gi ![]() pola
pola ![]() to
ten punkt jest asymptotycznie stabilny.
to
ten punkt jest asymptotycznie stabilny.
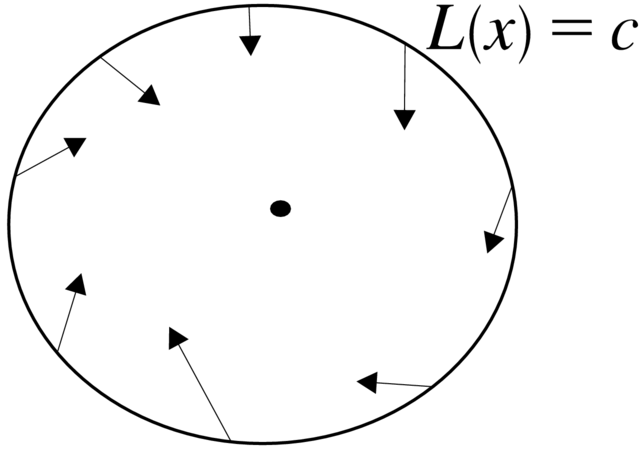
Dowód. Własność (i) z definicji funkcji Lapunowa mówi, że zbiory![]()
![]() , są ograniczone i dążą do punktu
, są ograniczone i dążą do punktu ![]() przy
przy ![]()
Własność (ii) oznacza, że jeśli ![]() jest rowiązaniem równania
jest rowiązaniem równania ![]() to
to
Widać, że funkcja Lapunowa maleje wzdłuż rozwiązań równania różniczkowego (patrz Rysunek 1.3).
Zatem rozwiązania startujące z brzegu ![]() zbioru
zbioru ![]() `wchodzą' do wnętrza tego
zbioru. Ponieważ te trajektorie pozostają w zbiorach
`wchodzą' do wnętrza tego
zbioru. Ponieważ te trajektorie pozostają w zbiorach ![]() jest spełniony warunek stabilności w sensie Lapunowa. Z
drugiej strony, rozwiązania muszą dążyć do punktu
jest spełniony warunek stabilności w sensie Lapunowa. Z
drugiej strony, rozwiązania muszą dążyć do punktu ![]() przy
przy ![]() a to oznacza asymptotyczną stabilność. ∎
a to oznacza asymptotyczną stabilność. ∎
Teraz dla dowodu twierdzenia Lapunowa wypada skonstruować funkcję
Lapunowa. W tym celu poprawimy nieco macierz ![]() Po pierwsze, założymy, że jest ona w postaci Jordana. Zatem mamy klatki
Po pierwsze, założymy, że jest ona w postaci Jordana. Zatem mamy klatki
![\left(\begin{array}[]{cccccc}\lambda _{{j}}&1&0&\ldots&0&0\\
0&\lambda _{{j}}&1&\ldots&0&0\\
\ldots&\ldots&\ldots&\ldots&\ldots&\ldots\\
0&0&0&\ldots&\lambda _{{j}}&1\\
0&0&0&\ldots&0&\lambda _{{j}}\end{array}\right),\text{ \ \ }\left(\begin{array}[]{ccccc}\alpha _{{j}}&-\beta _{{j}}&1&0&\ldots\\
\beta _{{j}}&\alpha _{{j}}&0&1&\ldots\\
0&0&\alpha _{{j}}&-\beta _{{j}}&\ldots\\
0&0&\beta _{{j}}&\alpha _{{j}}&\ldots\\
\ldots&\ldots&\ldots&\ldots&\ldots\end{array}\right),](wyklady/rrj/mi/mi322.png) |
odpowiadające nierzeczywistym (![]() i
zespolonym (
i
zespolonym (![]()
![]() ) wartościom własnym.
) wartościom własnym.
Okazuje się, że jedynki nad diagonalą można zastąpić
małymi ![]() ami. Rzeczywiście, jeśli mamy klatkę
Jordana wymiaru
ami. Rzeczywiście, jeśli mamy klatkę
Jordana wymiaru ![]() z rzeczywistą wartością własną
z rzeczywistą wartością własną ![]() to w standardowej bazie
to w standardowej bazie ![]() mamy
mamy
Zatem dla bazy ![]() takiej, że
takiej, że
będziemy mieli ![]() i
i ![]()
![]() Analogiczną zamianę stosujemy
w przypadku, gdy mamy klatkę Jordana z zepolonymi wartościami własnymi (Zadanie 1.27). Mamy zatem następujący
Analogiczną zamianę stosujemy
w przypadku, gdy mamy klatkę Jordana z zepolonymi wartościami własnymi (Zadanie 1.27). Mamy zatem następujący
Lemat 1.7.W odpowiednim liniowym układzie współrzędnych macierz ![]() przyjmuje postać
przyjmuje postać
gdzie ![]() jest blokowo-diagonalna z
jest blokowo-diagonalna z![]() i z
i z ![]() na diagonali a maciarz
na diagonali a maciarz ![]() jest ograniczona,
jest ograniczona, ![]()
Następny lemat kończy dowód Stwierdzenia 1.6.
Lemat 1.8.Niech ![]() będzie układem współrzędnych z tezy Lematu 1.7. Wtedy funkcja
będzie układem współrzędnych z tezy Lematu 1.7. Wtedy funkcja
na odpowiednio małym otoczeniu pnktu ![]() jest funkcją Lapunowa dla tego punktu równowagi.
jest funkcją Lapunowa dla tego punktu równowagi.
Dowód. Oczywiście wystarczy sprawdzić własność (ii) z Definicji 1.5 funkcji Lapunowa. Mamy
gdzie ![]() Pierwszy wyraz po prawej stronie tej równości wynosi (jak łatwo sprawdzić)
Pierwszy wyraz po prawej stronie tej równości wynosi (jak łatwo sprawdzić)
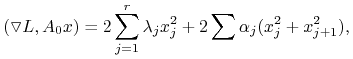 |
(1.5) |
gdzie w drugiej sumie sumujemy po ![]() Następnie, z
ograniczoności
Następnie, z
ograniczoności ![]() dostajemy
dostajemy
Poniewaz nieliniowe wyrazy pola ![]() są rzędu
są rzędu ![]() mamy
mamy
dla pewnej stałej ![]() i dostatecznie małego
i dostatecznie małego ![]()
Warunek (1.4) z założenia twierdzenia Lapunowa oznacza, że w (1.5) mamy
dla pewnego ![]() . Zatem mamy
. Zatem mamy ![]() a pozostałe dwa człony w
a pozostałe dwa człony w ![]() szacują się przez
szacują się przez ![]() To pokazuje, że
To pokazuje, że ![]() dla
dla ![]() i małego
i małego
![]() co kończy dowód lematu i twierdzenia Lapunowa.
∎
co kończy dowód lematu i twierdzenia Lapunowa.
∎
Istnieje twierdzenie odwrotne do twierdzenia Lapunowa. Jest ono dosyć naturalne i przypuszczalnie Lapunow miał jego świadomość, ale w rosyjskiej literaturze (np. w [10]) przypisuje się je V. Czetajewowi.
Twierdzenie 1.9 (Czetajew). Jeśli macierz ![]() linearyzacji pola wektorowego (1.3) posiada wartość własną o
ściśle dodatniej części rzeczywistej, to punkt równowagi
linearyzacji pola wektorowego (1.3) posiada wartość własną o
ściśle dodatniej części rzeczywistej, to punkt równowagi
![]() nie jest stabilny (ani w sensie Lapunowa ani asymptotycznie).
nie jest stabilny (ani w sensie Lapunowa ani asymptotycznie).
Dowód. Niech ![]() będą ściśle dodatnie a
będą ściśle dodatnie a ![]()
![]()
![]() Możemy założyć, że
Możemy założyć, że
w rozkładzie ![]() przy
czym macierz
przy
czym macierz ![]() ma wartości własne
ma wartości własne ![]() a macierz
a macierz ![]() ma wartości własne
ma wartości własne ![]() Ponadto, możemy założyć, że macierze
Ponadto, możemy założyć, że macierze ![]() i
i ![]() są jak w tezie Lematu 1.7. Przyjmijmy jeszcze, że
są jak w tezie Lematu 1.7. Przyjmijmy jeszcze, że
![]() w powyższym rozkładzie
w powyższym rozkładzie ![]() oraz
oraz ![]() .
.
Zdefiniujmy stożek ![]() za pomocą nierówności
za pomocą nierówności
gdzie stałe ![]() i
i ![]() będą zdefiniowanie w trakcie
dalszych etapów dowodu. Zauważmy, że brzeg
będą zdefiniowanie w trakcie
dalszych etapów dowodu. Zauważmy, że brzeg ![]() stożka
stożka ![]() składa się z dwóch części:
składa się z dwóch części:
![]() i
i ![]() Zdefiniujmy też `funkcję
Czetajewa', jako
Zdefiniujmy też `funkcję
Czetajewa', jako
Okazuje się, że przy odpowiednio dobranych ![]() i
i ![]() zachodzą następujące własności:
zachodzą następujące własności:
(a) pole wektorowe wchodzi do ![]() na częsci
na częsci ![]() brzegu,
brzegu,
(b) ![]() dla
dla ![]() Oczywiście, z nich wynika teza twierdzenia; trajektorie startujące
dowolnie blisko
Oczywiście, z nich wynika teza twierdzenia; trajektorie startujące
dowolnie blisko ![]() w
w ![]() wychodzą z
wychodzą z ![]() przez część
przez część ![]() brzegu (patrz Rysunek 1.4).
brzegu (patrz Rysunek 1.4).
Aby udowodnić te własności, skorzystamy z nierówności (które są konsekwencją poczynionych założeń):
(dla ![]() i małego
i małego ![]() przy warunku, że
przy warunku, że ![]() (
(![]() dostatecznie małe). Jak zwykle
dostatecznie małe). Jak zwykle ![]() oznacza pochodną wzdłuż trajektorii
oznacza pochodną wzdłuż trajektorii ![]() pola wektorowego.
pola wektorowego.
Warunek (a) oznacza, że ![]() Ale dla
Ale dla ![]() mamy
mamy
o ile ![]() jest małe. Z drugiej strony dla
jest małe. Z drugiej strony dla ![]() mamy
mamy
∎
W związku z powyższymi twierdzeniami nasuwa się naturalne praktyczne pytanie:
jak sprawdzić, czy wszystkie wartości własne danej macierzy mają ujemne częsci rzeczywiste?
Oczywiście to pytanie sprowadza się do pytania o części rzeczywiste pierwiastków wielomianu charakterystycznego tej macierzy.
Zatem załóżmy, że mamy wielomian2Wielomian charakterystyczny macierzy ![]() ma współczynnik
ma współczynnik ![]() Tutaj przyjmujemy
Tutaj przyjmujemy ![]() dla
uproszcenia formułowanych niżej wyników.
dla
uproszcenia formułowanych niżej wyników.
| (1.6) |
Definicja 1.10. Mówimy, że wielomian ![]() jest
stabilny jeśli wszystkie jego zera
jest
stabilny jeśli wszystkie jego zera ![]() mają ujemną część rzeczywistą.
mają ujemną część rzeczywistą.
Pytamy o warunki konieczne i dostateczne aby wielomian postaci (1.6) był stabilny. Okazuje się, że ten problem był badany już w XIX wieku i ma pełne rozwiązanie.
Aby przyjrzeć się temu zagadnieniu, odnotujmy następujący prosty warunek konieczny.
Lemat 1.11.Jeśli wielomian postaci (1.6) jest
stabilny, to ![]() dla wszystkich
dla wszystkich![]()
Dowód. Przyjrzyjmy się czynnikom w przedstawieniu
gdzie pierwszy iloczyn jest związany z rzeczywistymi pierwiastkami ![]() a drugi iloczyn jest związany z nierzeczywistymi
pierwiastkami
a drugi iloczyn jest związany z nierzeczywistymi
pierwiastkami ![]()
![]()
![]() Ponieważ każdy z czynników ma dodatnie współczynniki, to i cały wielomian też musi mieć dodatnie współczynniki. ∎
Ponieważ każdy z czynników ma dodatnie współczynniki, to i cały wielomian też musi mieć dodatnie współczynniki. ∎
Uwaga 1.12. Jeśli stopień ![]() to warunek
to warunek ![]()
![]() jest również warunkiem dostateczym.
jest również warunkiem dostateczym.
Zdefiniujmy następującą macierz wymiaru ![]()
![M=\left[\begin{array}[]{lllllll}a_{{1}}&a_{{0}}&0&0&\ldots&0&0\\
a_{{3}}&a_{{2}}&a_{{1}}&a_{{0}}&\ldots&0&0\\
a_{{5}}&a_{{4}}&a_{{3}}&a_{{2}}&\ldots&0&0\\
\ldots&\ldots&\ldots&\ldots&\ldots&\ldots&\ldots\\
0&0&0&0&\ldots&a_{{n-1}}&a_{{n-2}}\\
0&0&0&0&\ldots&0&a_{{n}}\end{array}\right]](wyklady/rrj/mi/mi441.png) |
(1.7) |
taką, że na diagonali stoją kolejno liczby ![]()
Twierdzenie 1.13 (Warunki Raussa–Hurwitza). Warunkiem koniecznym i dostatecznym na stabilność wielomianu (1.6) jest:
(i) ![]() dla wszystkich
dla wszystkich ![]()
(ii) minory główne ![]() (wymiarów
(wymiarów ![]() macierzy (1.7) są dodatnie.
macierzy (1.7) są dodatnie.
Przykłady 1.14. Dla ![]() macierz (1.7) ma postać
macierz (1.7) ma postać ![]() zatem
zatem ![]()
Dla ![]() czyli macierzy
czyli macierzy ![]() mamy
mamy ![]() i
i ![]() zatem odtwarzamy
Uwagę 1.12.
zatem odtwarzamy
Uwagę 1.12.
Dla ![]() mamy macierz
mamy macierz
![\left[\begin{array}[]{ccc}a_{{1}}&a_{{0}}&0\\
a_{{3}}&a_{{2}}&a_{{1}}\\
0&0&a_{{3}}\end{array}\right].](wyklady/rrj/mi/mi197.png) |
Warunki Raussa–Hurwitza przyjmują postać: ![]() (nic nowego),
(nic nowego),
| (1.8) |
i ![]() (też nic nowego).
(też nic nowego).
Uwaga 1.15. Można pokazać, że warunek ![]() dla wszystkich
dla wszystkich ![]() można zastąpić następującym warunkiem Liénarda–Shapira:
można zastąpić następującym warunkiem Liénarda–Shapira:
(patrz także poniższy dowód).
Dowód Twierdzenia 1.13.3Na wykładzie dowód jest ograniczony do przypadku ![]() i tego wymaga się od studentów na egzaminie. Idea dowodu jest dosyć prosta.
Warunki
i tego wymaga się od studentów na egzaminie. Idea dowodu jest dosyć prosta.
Warunki![]() (oraz
(oraz ![]() ) definiują
pewien podzbiór
) definiują
pewien podzbiór ![]() w przestrzeni
w przestrzeni ![]() współczynników
współczynników ![]() Zbiór
Zbiór ![]() jest semi-algebraiczny i
jego brzeg składa się z gładkich `stratów'. Chodzi o równania definiujące te straty. Jeśli
jest semi-algebraiczny i
jego brzeg składa się z gładkich `stratów'. Chodzi o równania definiujące te straty. Jeśli ![]() , to mamy dwie
możliwości: albo
, to mamy dwie
możliwości: albo
(a) pewien pierwiastek równania ![]() zeruje się,
albo
zeruje się,
albo
(b) para sprzężonych pierwiastków zespolonych leży na osi urojonej.
Przypadek (a) oznacza, że ![]() czyli
czyli ![]() ; to jest
dosyć proste.
; to jest
dosyć proste.
Rozważmy sytuację z parą ![]() urojonych pierwiastków. Mamy wtedy
urojonych pierwiastków. Mamy wtedy
| (1.9) |
dla pewnego wielomianu
o którym możemy założyć, że jest stabilny. Ponadto, z
założenia indukcyjnego (względem ![]() możemy przyjąć,
że
możemy przyjąć,
że ![]() i odpowiednie minory
i odpowiednie minory ![]()
Mamy następujące relacje
To oznacza, że macierz ![]() w (1.7) ma pos
tać
w (1.7) ma pos
tać ![]() gdzie
gdzie
![M_{{1}}=\left[\begin{array}[]{ccccccc}b_{{1}}&b_{{0}}&0&\ldots&0&0&0\\
b_{{3}}&b_{{2}}&b_{{1}}&\ldots&0&0&0\\
b_{{5}}&b_{{4}}&b_{{3}}&\ldots&0&0&0\\
\ldots&\ldots&\ldots&\ldots&\ldots&\ldots&\ldots\\
0&0&0&\ldots&b_{{n-2}}&b_{{n-3}}&b_{{n-4}}\\
0&0&0&\ldots&0&0&b_{{n-2}}\\
0&0&0&\ldots&0&0&0\end{array}\right],](wyklady/rrj/mi/mi433.png) |
![M_{{2}}=\left[\begin{array}[]{ccccccc}0&0&0&\ldots&0&0&0\\
b_{{1}}&b_{{0}}&0_{{1}}&\ldots&0&0&0\\
b_{{3}}&b_{{2}}&b_{{1}}&\ldots&0&0&0\\
\ldots&\ldots&\ldots&\ldots&\ldots&\ldots&\ldots\\
0&0&0&\ldots&b_{{n-4}}&b_{{n-5}}&b_{{n-6}}\\
0&0&0&\ldots&b_{{n-2}}&b_{{n-3}}&b_{{n-4}}\\
0&0&0&\ldots&0&0&b_{{n-2}}\end{array}\right].](wyklady/rrj/mi/mi372.png) |
Zauważmy, że ![]() ty wiersz macierzy
ty wiersz macierzy ![]() równa się
równa się ![]() temu wierszowi macierzy
temu wierszowi macierzy ![]() dla
dla ![]() To oznacza, że
wszystkie minory
To oznacza, że
wszystkie minory ![]()
![]() macierzy
macierzy ![]() są równe odpowiednim minorom
są równe odpowiednim minorom ![]() dla macierzy
dla macierzy ![]() (związanej z wielomianem
(związanej z wielomianem ![]() zatem są one dodatnie. Stąd też wynika, że
zatem są one dodatnie. Stąd też wynika, że ![]() i
i ![]()
Widać, że równanie ![]() opisuje lokalnie hiperpłaszczyznę w przestrzeni współczynników
opisuje lokalnie hiperpłaszczyznę w przestrzeni współczynników ![]() oddzielającą wielomiany stabilne od nie-
stabilnych. Wypada tylko sprawdzić, czy nierówność
oddzielającą wielomiany stabilne od nie-
stabilnych. Wypada tylko sprawdzić, czy nierówność ![]() lokalnie definiuje zbiór wielomianów
stabilnych.
lokalnie definiuje zbiór wielomianów
stabilnych.
W tym celu rozważymy następującą deformację sytuacji (1.9):
gdzie parametr ![]() jest mały i
jest mały i ![]() jest rzeczywiste. Wtedy do
macierzy
jest rzeczywiste. Wtedy do
macierzy ![]() dochodzi jeszcze jeden człon
dochodzi jeszcze jeden człon ![]() gdzie w
ostatnich dwóch wierszach macierzy
gdzie w
ostatnich dwóch wierszach macierzy ![]() niezerowy jest tylko końcowy fragment wymiaru
niezerowy jest tylko końcowy fragment wymiaru ![]()
Gdy ![]() i
i ![]() są niezerowe wielomian
są niezerowe wielomian ![]() jest stabilny; zatem
jest stabilny; zatem ![]() dla
dla ![]() Policzmy granicę
Policzmy granicę ![]() przy
przy ![]() i stałym
i stałym ![]() (Wtedy
(Wtedy ![]() bo
bo ![]() ale to nam nie przeszkadza.) Łatwo zobaczyć, że dla
ale to nam nie przeszkadza.) Łatwo zobaczyć, że dla ![]() i małego niezerowego
i małego niezerowego ![]() macierz
macierz ![]() przyjmuje postać blokową, z blokami:
przyjmuje postać blokową, z blokami: ![]() (wymiaru
(wymiaru ![]()
![]() (wymiaru
(wymiaru ![]()
![]() (wymiaru
(wymiaru ![]() i
i ![]() Ponieważ
Ponieważ ![]() jest bliskie
jest bliskie ![]() (z założenia indukcyjnego), więc i
(z założenia indukcyjnego), więc i ![]() Zatem
Zatem
∎
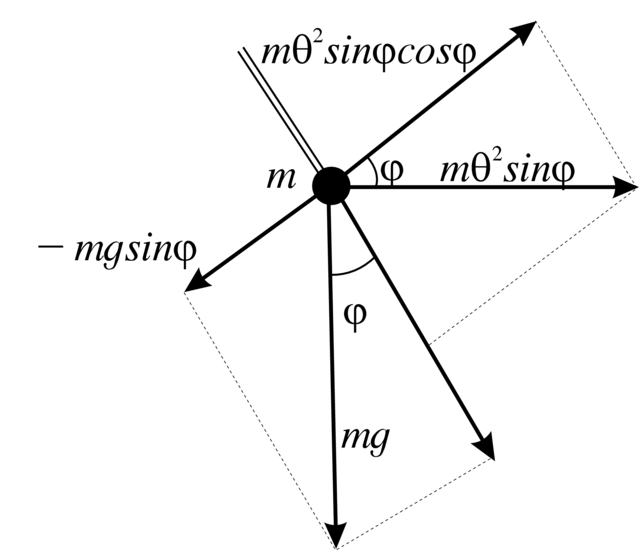
Przykład 1.16 (Regulator Watta). Na Rysunku 1.5 mamy przedsta- wiony schemat regulatora Watta, stosowanego w XIX wieku w maszynach parowych. Ten regulator składa się z:
— sworznia ![]() który może się obracać wokół swojej
osi;
który może się obracać wokół swojej
osi;
— dwu kul o masie ![]() każda, umieszczonych na ruchomych przegubach wokół sworznia
każda, umieszczonych na ruchomych przegubach wokół sworznia ![]() , tak, że górna obręcz jest nieruchoma
(scalona z
, tak, że górna obręcz jest nieruchoma
(scalona z ![]() ) a dolna obręcz może przesuwać się w górę i w dół (przy czym kule odpowiednio oddalają się od
sworznia i przybliżają do sworznia), ponadto pręty
) a dolna obręcz może przesuwać się w górę i w dół (przy czym kule odpowiednio oddalają się od
sworznia i przybliżają do sworznia), ponadto pręty ![]() i
i ![]() łaczące kule z górną obręczą mają długość
łaczące kule z górną obręczą mają długość ![]() ;
;
— koła zamachowego ![]() umieszczonego na walcu
umieszczonego na walcu ![]()
— przekładni zębatej pomiędzy sworzniem ![]() i walcem
i walcem ![]() o
stosunku prędkości obrotowych
o
stosunku prędkości obrotowych ![]()
— dźwigni ![]() regulującej dopływ pary do maszyny i
przymocowanej do dolnej obręczy.
regulującej dopływ pary do maszyny i
przymocowanej do dolnej obręczy.
Na każdą kulę działają trzy siły (patrz Rusunek 1.6): siła odśrodkowa ![]() (skierowana prostopadle od sworznia na zewnątrz), siła ciężkości
(skierowana prostopadle od sworznia na zewnątrz), siła ciężkości ![]() (skierowana w dół) oraz tarcie
(skierowana w dół) oraz tarcie ![]() (prostopadłe do prętów
(prostopadłe do prętów ![]() ). Tutaj
). Tutaj ![]() jest prędkością kątową obrotu sworznia
jest prędkością kątową obrotu sworznia ![]() (i kul),
(i kul), ![]() jest kątem pomiędzy prętami
jest kątem pomiędzy prętami ![]() a sworzniem
a sworzniem ![]()
![]() jest przyspieszeniem ziemskim a
jest przyspieszeniem ziemskim a ![]() jest pewnym współczynnikiem. Sumując składowe tych sił prostopadłe do prętów
jest pewnym współczynnikiem. Sumując składowe tych sił prostopadłe do prętów ![]() dostajemy następujące równanie ruchu
dostajemy następujące równanie ruchu
| (1.10) |
Przy tym zwykle zakłada się (np. w [16]), że
tj. w pewnych jednoskach długości.
W równaniu (1.10) oprócz dynamicznej zmiennej ![]() występuje jeszcze wielkość
występuje jeszcze wielkość ![]() która także zmienia się
z czasem. Aby dostać jakąś zależność
która także zmienia się
z czasem. Aby dostać jakąś zależność ![]() (lub
jej pochodnych) od
(lub
jej pochodnych) od ![]() uwzględnijmy najpierw jej związek
uwzględnijmy najpierw jej związek
z prędkością obrotową ![]() walca
walca ![]() Z drugiej strony,
ruch koła zamachowego
Z drugiej strony,
ruch koła zamachowego ![]() opisuje się równaniem
opisuje się równaniem
gdzie ![]() jest momentem bezwładności koła, natomiast po prawej
stronie mamy moment siły działającej na koło. Przy tym składnik
jest momentem bezwładności koła, natomiast po prawej
stronie mamy moment siły działającej na koło. Przy tym składnik ![]() jest proporcjonalny do ilości dopływu pary (
jest proporcjonalny do ilości dopływu pary (![]() jest pewną stałą) a
jest pewną stałą) a ![]() jest stałą spowalniającą siłą związaną z pracą wykonywaną przez maszynę. Z
powyższych rozważań wynika następujący zamknięty i
autonomiczny układ równań różniczkowych dla
jest stałą spowalniającą siłą związaną z pracą wykonywaną przez maszynę. Z
powyższych rozważań wynika następujący zamknięty i
autonomiczny układ równań różniczkowych dla ![]()
![]() i
i ![]()
![\begin{array}[]{lll}\dot{x}&=&y,\\
\dot{y}&=&n^{{2}}z^{{2}}\sin x\cos x-g\sin x-\frac{b}{m}y,\\
\dot{z}&=&\frac{k}{J}\cos x-\frac{F}{J},\end{array}](wyklady/rrj/mi/mi404.png) |
(1.11) |
Okazuje się, że ten układ ma dokładnie jedno (fizycznie
realizowalne) położenie równowagi ![]() zadane równaniami
zadane równaniami
| (1.12) |
Ponadto macierz linearyzacji układu (1.11) w tym punkcie równowagi jest następująca
![A=\left[\begin{array}[]{ccc}0&1&0\\
-g\frac{\sin^{{2}}x_{{0}}}{\cos x_{{0}}}&-\frac{b}{m}&2g\frac{\sin x_{{0}}}{z_{{0}}}\\
-\frac{k}{J}\sin x_{{0}}&0&0\end{array}\right]](wyklady/rrj/mi/mi257.png) |
(1.13) |
a jej wielomian charakterystyczny to
| (1.14) |
Widać, że współczynniki wielomianu ![]() są
dodatnie, czyli jest spełniony warunek (i) Twierdzenia Raussa–Hurwiza. Dzięki Przykładowi 1.14 (dla
są
dodatnie, czyli jest spełniony warunek (i) Twierdzenia Raussa–Hurwiza. Dzięki Przykładowi 1.14 (dla ![]() warunkiem dostatecznym stabilności wielomian
warunkiem dostatecznym stabilności wielomian ![]() jest nierówność (1.8), która w
tym przypadku oznacza
jest nierówność (1.8), która w
tym przypadku oznacza
| (1.15) |
(Zadanie 1.28). Tutaj ![]() ma mechaniczną
interpretację nierównomierności pracy maszyny. Zatem
ostatnia nierówność przyjmuje prostą postać
ma mechaniczną
interpretację nierównomierności pracy maszyny. Zatem
ostatnia nierówność przyjmuje prostą postać
Można stąd wysnuć następujące wnioski:
— zwiększanie masy ![]() kul pogarsza stabilność;
kul pogarsza stabilność;
— zmniejszanie współczynnika tarcia ![]() pogarsza stabilność;4Gdy prezentowałem ten przykład kilka lat temu na wykładzie z JTRRZ, Z.
Nowak poinformował nas o przypadkach, gdy w niektórych fabrykach
niemieckich (gdzie dbano o wszystko) uporczywe zmniejsznie współczynnika tarcia prowadziło do awarii maszyn parowych.
pogarsza stabilność;4Gdy prezentowałem ten przykład kilka lat temu na wykładzie z JTRRZ, Z.
Nowak poinformował nas o przypadkach, gdy w niektórych fabrykach
niemieckich (gdzie dbano o wszystko) uporczywe zmniejsznie współczynnika tarcia prowadziło do awarii maszyn parowych.
— zmniejszenie momentu bezwładności ![]() koła zamachowego
pogarsza stabilność;
koła zamachowego
pogarsza stabilność;
— podobny wpływ ma zmniejszenie współczynnika ![]() nierównomierności pracy maszyny.
nierównomierności pracy maszyny.
1.2. Hiperboliczność
Wyniki poprzedniego rozdziału nauczyły nas, że warunek ![]() dla pewnej wartości własnej macierzy linearyzacji
dla pewnej wartości własnej macierzy linearyzacji ![]() w punkcie równowagi autonomicznego pola wektorowego
w punkcie równowagi autonomicznego pola wektorowego
| (1.16) |
jest warunkiem granicznym dla roztrzygnięcia problemy stabilności asymptotycznej tego punktu równowagi. Stąd pojawia się następująca
Definicja 1.17. Punkt równowagi ![]() autonomicznego pola
wektorowego (1.16) nazywa się punktem hiperbolicznym, jeśli
części rzeczywiste wszystkich wartości własnych macierzy
autonomicznego pola
wektorowego (1.16) nazywa się punktem hiperbolicznym, jeśli
części rzeczywiste wszystkich wartości własnych macierzy ![]() linearyzacji pola w tym punkcie są niezerowe.
linearyzacji pola w tym punkcie są niezerowe.
Załóżmy, że punkt ![]() jest hiperboliczny i rozważmy
odpowiedni układ liniowy
jest hiperboliczny i rozważmy
odpowiedni układ liniowy
| (1.17) |
Wtedy istnieje naturalny rozkład przestrzeni ![]() na sumę
prostą podprzestrzeni stabilnej
na sumę
prostą podprzestrzeni stabilnej ![]() i
podprzestrzeni niestabilnej
i
podprzestrzeni niestabilnej ![]() (od angielskich słów `stable' i `unstable'), odpowiadających wartościom własnym z
(od angielskich słów `stable' i `unstable'), odpowiadających wartościom własnym z ![]() i z
i z ![]() odpowiednio:
odpowiednio:
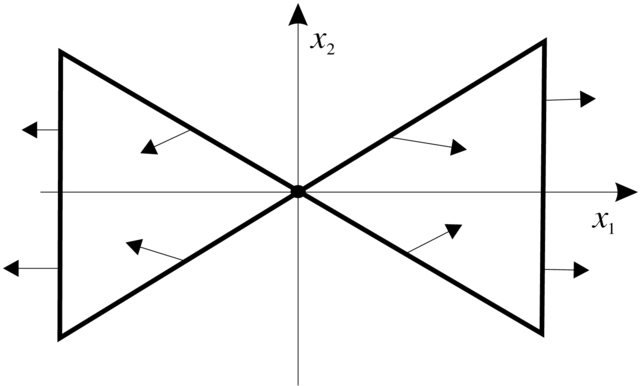
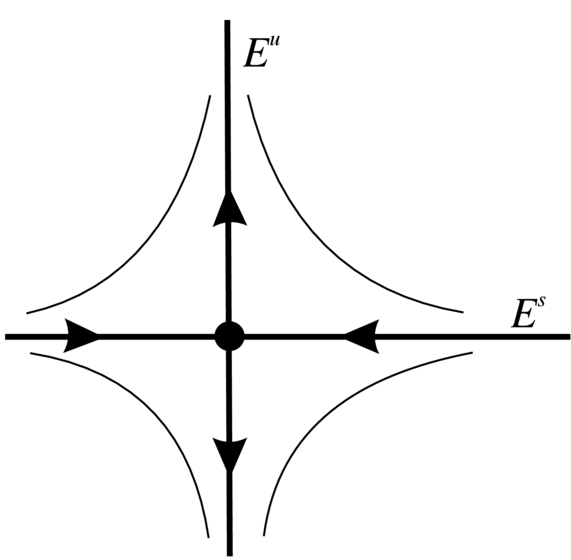
| (1.18) |
Zauważmy, że podprzestrzenie ![]() i
i ![]() można zdefiniować topologicznie w terminach liniowego potoku fazowego
można zdefiniować topologicznie w terminach liniowego potoku fazowego ![]() liniowego pola (1.17) (patrz Dodatek). Mianowicie
liniowego pola (1.17) (patrz Dodatek). Mianowicie
(patrz Rysunek 1.7).
Okazuje się, że analogiczna sytuacja ma miejsce w przypadku nieliniowego pola (1.16).
Twierdzenie 1.18 (Hadamard–Perron). Dla hiperbolicznego
punktu równowagi ![]() pola
pola ![]() klasy
klasy ![]()
![]() , istnieją lokalne podrozmaitości, stabilna
, istnieją lokalne podrozmaitości, stabilna ![]() i niestabilna
i niestabilna ![]() klasy
klasy ![]() , takie, że
, takie, że
| (1.19) |
oraz5Tutaj ![]() oznacza lokalny potok fazowy generowany przez pole
oznacza lokalny potok fazowy generowany przez pole ![]() a
a ![]() oznacza przestrzeń styczną do podrozmaitości
oznacza przestrzeń styczną do podrozmaitości ![]() w
punkcie
w
punkcie ![]()
| (1.20) |
Zanim zabierzemy się za dowód tego twierdzenia, zauważmy, że
analogiczne pojęcia i twierdzenia można wprowadzić dla
lokalnych dyfeomeorfizmów. Po pierwsze, jeśli ![]() jest punktem równowagi pola wektorowego
jest punktem równowagi pola wektorowego ![]() to
to ![]() jest
punktem stałym przekształcenia potoku po czasie
jest
punktem stałym przekształcenia potoku po czasie ![]()
![]() tzn.
tzn.
Ponadto część liniowa ![]() przekształcenia
przekształcenia ![]() w
w ![]() ma postać macierzy
ma postać macierzy
(Zadanie 1.36). W istocie istnieje dyskretna wersja pojęcia potoku fazowego.
Definicja 1.19. Dyfeomorfizm ![]() definiuje
homomorfizm
definiuje
homomorfizm ![]() z grupy addytywnej liczb całkowitych do grupy dyfeomeorfizmów rozmaitości tak, że
z grupy addytywnej liczb całkowitych do grupy dyfeomeorfizmów rozmaitości tak, że
gdzie ![]() (
(![]() razy dla
razy dla ![]() i
i ![]() (
(![]() razy
dla
razy
dla ![]() W literaturze
W literaturze ![]() nazywa się kaskadą.
nazywa się kaskadą.
Punkt ![]() jest punktem okresowym o okresie
jest punktem okresowym o okresie ![]() dla
dla ![]() , jeśli
, jeśli ![]() przy tym pod okresem będziemy
rozumieli minimalny okres (tzn.
przy tym pod okresem będziemy
rozumieli minimalny okres (tzn. ![]() dla
dla ![]() Oczywiście punkt okresowy o okresie
Oczywiście punkt okresowy o okresie ![]() jest punktem stałym.
jest punktem stałym.
Definicja 1.20. Punkt okresowy ![]() o okresie
o okresie ![]() dyfeomorfizmu
dyfeomorfizmu
![]() nazywa się hiperbolicznym, jeśli macierz
nazywa się hiperbolicznym, jeśli macierz
ma wszystkie wartości własne poza okręgiem jednostkowym,
Lemat 1.21.Jeśli ![]() jest hiperbolicznym
punktem równowagi pola wektorowego
jest hiperbolicznym
punktem równowagi pola wektorowego ![]() to
to ![]() jest też hiperbolicznym punktem stałym dyfeomorfizmu
jest też hiperbolicznym punktem stałym dyfeomorfizmu ![]() , i odwrotnie (Zadanie 1.36).
, i odwrotnie (Zadanie 1.36).
Mamy następującą wersję twierdzenia Hadamarda–Perrona dla dyfeomorfizmów.
Twierdzenie 1.22.Jeśli punkt stały ![]() lokalnego dyfeomorfizmu
lokalnego dyfeomorfizmu![]() klasy
klasy ![]()
![]() jest hiperboliczny, to istnieją lokalne
podrozmaitości, stabilna
jest hiperboliczny, to istnieją lokalne
podrozmaitości, stabilna ![]() i niestabilna
i niestabilna ![]() klasy
klasy ![]() , takie, że
, takie, że
| (1.21) |
oraz
| (1.22) |
gdzie ![]() i
i ![]() są podprzestrzniami
są podprzestrzniami![]() rozpiętymi przez podprzestrzenie własne
odpowiadające wartościom własnym macierzy
rozpiętymi przez podprzestrzenie własne
odpowiadające wartościom własnym macierzy ![]() o module
o module ![]() i
i ![]() odpowiednio.
odpowiednio.
Droga do dowodu Twierdzenia Hadamarda–Perrona 1.18 wiedzie poprzez dowód Twierdzenia 1.22. Przy tym, jak się wkrótce przekonamy, metoda
dowodu istnienia podrozmaitościi ![]() i
i ![]() o własnościach (1.21) klasy
o własnościach (1.21) klasy ![]() jest dosyć naturalna: dostaje się równanie na punkt stały pewnego przekształcenia w odpowiedniej nieskończenie wymiarowej przestrzeni Banacha. Niestety `wyciśnięcie'
warunku kontrakcji tego przekształcenia jest mocno wyczerpujące.
Dlatego w poniższym dowodzie ograniczymy się do wyprowadzenie
odpowiednich równań i naszkicujemy ogólny schemat
oszacowań. Po ścisły dowód odsyłamy czytelnika do monografii
W. Szlenka [18].
jest dosyć naturalna: dostaje się równanie na punkt stały pewnego przekształcenia w odpowiedniej nieskończenie wymiarowej przestrzeni Banacha. Niestety `wyciśnięcie'
warunku kontrakcji tego przekształcenia jest mocno wyczerpujące.
Dlatego w poniższym dowodzie ograniczymy się do wyprowadzenie
odpowiednich równań i naszkicujemy ogólny schemat
oszacowań. Po ścisły dowód odsyłamy czytelnika do monografii
W. Szlenka [18].
Dowód Twierdzenia 1.22. Dla uproszczenia sytuacji załóżmy rozkład(1.18), czyli ![]() i przekształcenie w postaci
i przekształcenie w postaci ![]() takie, że
takie, że
| (1.23) |
gdzie
| (1.24) |
oraz funkcje ![]() i
i ![]() są rzędu
są rzędu ![]() (Zadanie 1.37).
(Zadanie 1.37).
Oczywiście wektorowe funkcje ![]() i
i ![]() są określone w małym otoczeniu zera. W dowodzie, który predstawiamy poniżej, stanowi to pewną techniczną przeszkodę. Dlatego dokonamy następującej zamiany
są określone w małym otoczeniu zera. W dowodzie, który predstawiamy poniżej, stanowi to pewną techniczną przeszkodę. Dlatego dokonamy następującej zamiany
gdzie funkcja ![]() jest gładka (klasy
jest gładka (klasy ![]() ) i taka, że:
) i taka, że:
(i) ![]() w małym otoczeniu zera,
w małym otoczeniu zera, ![]() ;
;
(ii) ![]() poza małym otoczeniem zera,
poza małym otoczeniem zera, ![]() (Zadanie 1.38).
Zatem funkcje
(Zadanie 1.38).
Zatem funkcje ![]() i
i ![]() po przedłużeniu zerem
dla
po przedłużeniu zerem
dla ![]() będą określone na całym
będą określone na całym ![]() Dalej oznaczamy je przez
Dalej oznaczamy je przez ![]() i
i ![]() Przypomnijmy, że te nowe funkcje spełniają
Przypomnijmy, że te nowe funkcje spełniają ![]()
![]() oraz
oraz ![]() i
i ![]() są małe wraz z pochodnymi. Dzięki własności (i) dynamika przekształcenia
są małe wraz z pochodnymi. Dzięki własności (i) dynamika przekształcenia ![]() z nowymi
z nowymi ![]() i
i ![]() w otoczeniu zera jest taka sama jak dla starego przekształcenia
(1.23).
w otoczeniu zera jest taka sama jak dla starego przekształcenia
(1.23).
Poszukujemy podrozmaitości ![]() w postaci wykresu pewnego
odwzorowania (lub funkcji wektorowej)
w postaci wykresu pewnego
odwzorowania (lub funkcji wektorowej) ![]()
(Dowód istnienia podrozmaitości ![]() przebiega zupełnie
analogicznie, dlatego ograniczamy się do przypadku
przebiega zupełnie
analogicznie, dlatego ograniczamy się do przypadku ![]() .)
.)
Z własności (1.21) wynika, że podrozmaitość ![]() powinna być niezmiennicza względem dyfeomorfizmu
powinna być niezmiennicza względem dyfeomorfizmu ![]()
![]() To oznacza, że
To oznacza, że ![]() dla
pewnych
dla
pewnych ![]() zależnych od
zależnych od ![]() Z (1.23)
znajdujemy, że
Z (1.23)
znajdujemy, że ![]() Zatem dostajemy warunek
Zatem dostajemy warunek
który przepiszemy w następującej postaci
| (1.25) |
Traktujemy ostatnie równanie jako równanie punktu stałego ![]() dla nieliniowego operatora
dla nieliniowego operatora ![]() definiowanego przez
prawą stronę tej równości.
definiowanego przez
prawą stronę tej równości.
Zakładając, że funkcje ![]() i
i ![]() są klasy
są klasy ![]() ,
naturalne jest wprowadzić przestrzeń Banacha
,
naturalne jest wprowadzić przestrzeń Banacha ![]() odwzorowań ciągłych z normą supremum.
Nietrudno też pokazać, że przekształcenie
odwzorowań ciągłych z normą supremum.
Nietrudno też pokazać, że przekształcenie ![]() przeprowadza
przeprowadza ![]() w siebie. Aby zastosować zasadę Banacha
dla odwzorowań zwężających, należałoby jeszcze
udowodnić warunek kontrakcji, czyli oszacować normę różnicy
w siebie. Aby zastosować zasadę Banacha
dla odwzorowań zwężających, należałoby jeszcze
udowodnić warunek kontrakcji, czyli oszacować normę różnicy ![]() Tutaj pojawia się
problem, bo z (1.25) dostajemy następującą nierówność:
Tutaj pojawia się
problem, bo z (1.25) dostajemy następującą nierówność:
(Zadanie 1.39). Ponieważ ![]() (patrz
(1.24)) oraz
(patrz
(1.24)) oraz ![]() i
i ![]() są małe (patrz powyżej), to wypada tylko umieć
oszacować normę pochodnej
są małe (patrz powyżej), to wypada tylko umieć
oszacować normę pochodnej ![]() odwzorowania
odwzorowania ![]() Ale, jeśli wybieramy
Ale, jeśli wybieramy ![]() i
i ![]() dowolnie z przestrzni
dowolnie z przestrzni ![]() , to
, to ![]() będzie tylko ciągłe, a jego pochodna może być nieograniczona.
będzie tylko ciągłe, a jego pochodna może być nieograniczona.
Jest wyjście z tego impasu. Przypomnijmy, że w dowodzie twierdzenia
Banacha wybiera się ![]() a następnie punkty
a następnie punkty ![]() powinny zbiegać do punktu stałego.
Chodzi o to aby wybrać wektorową funkcję
powinny zbiegać do punktu stałego.
Chodzi o to aby wybrać wektorową funkcję ![]() gładką i
pokazać, że funkcje
gładką i
pokazać, że funkcje ![]() też są gładkie z odpowiednio
ograniczonymi normami. Nietrudno zgadnąć, że
też są gładkie z odpowiednio
ograniczonymi normami. Nietrudno zgadnąć, że
jest dibrym wyborem. Łatwo też widać ze wzoru (1.24), że ![]() są gładkie, np.
są gładkie, np. ![]()
Trzeba tylko pokazać, że funkcje ![]() są jednakowo ciągłe. To sprowadza się do oszacowania normy pochodnej
są jednakowo ciągłe. To sprowadza się do oszacowania normy pochodnej ![]() przy założeniu, ograniczoności
normy
przy założeniu, ograniczoności
normy ![]() Mamy
Mamy
| (1.26) |
gdzie pominęliśmy argumenty funkcji występujących po prawej stronnie tej równości. Zatem norma supremum szacuje się następująco:
gdzie ![]() jest małe,
jest małe, ![]() i
i ![]() Stąd wynika, że, jeśli
Stąd wynika, że, jeśli ![]() jest dostatecznie mała,
jest dostatecznie mała, ![]() (dla odpowiedniego
(dla odpowiedniego ![]() ), to i
), to i ![]() (Zadanie 1.40). To daje równomierne oszacowanie dla norm
(Zadanie 1.40). To daje równomierne oszacowanie dla norm ![]() ciągu funkcji
ciągu funkcji ![]()
Zatem ![]() zbiegają do punktu stałego
zbiegają do punktu stałego ![]() o którym na
razie możemy powiedzieć tylko że jest reprezentowany przez ciągłe odwzorowanie z
o którym na
razie możemy powiedzieć tylko że jest reprezentowany przez ciągłe odwzorowanie z ![]() do
do ![]() ; czyli, że podrozmaitość
; czyli, że podrozmaitość
jest klasy ![]()
Powiemy krótko, jak dowieść gładkości funkcji ![]() W tym celu należy stosować jednocześnie równania (1.25) i
(1.26) do ciągów
W tym celu należy stosować jednocześnie równania (1.25) i
(1.26) do ciągów ![]() i
i ![]() W szczególności, pokazuje się jednakową ciągłość rodziny
W szczególności, pokazuje się jednakową ciągłość rodziny ![]() co wymaga
jednostajnego szacowania wyrażenia
co wymaga
jednostajnego szacowania wyrażenia ![]() .Okazuje się, że to daje się zrobić korzystając z oszacowań dla
.Okazuje się, że to daje się zrobić korzystając z oszacowań dla![]()
![]() ,
, ![]() .
.
Następnie korzysta się z twierdzenia Ascoliego, które mówi,
że z jednakowo ciągłego ciągu funkcji na zwartym zbiorze można wybrać podciąg zbieżny. Tutaj zbiór zwarty to ![]() dla pewnego
dla pewnego ![]() a
granicą podciągu
a
granicą podciągu ![]() musi być
musi być ![]() (bo taka jest granica w przestrzeni funkcji ciągłych).
(bo taka jest granica w przestrzeni funkcji ciągłych).
W tym (skróconym) dowodzie ograniczyliśmy się do przypadku, gdy ![]() jest klasy
jest klasy ![]() (i wtedy
(i wtedy ![]() są też klasy
są też klasy ![]() Ale
przypadek klasy
Ale
przypadek klasy ![]() dla
dla ![]() też da się udowodnić, i to tą samą metodą, tylko dowód wymaga większej liczby wzorów i oszacowań. Pomijamy go.
też da się udowodnić, i to tą samą metodą, tylko dowód wymaga większej liczby wzorów i oszacowań. Pomijamy go.
Na koniec zauważmy, że ponieważ ![]() i
i ![]() i
i ![]() to mamy
to mamy ![]() dla dowolnego
dla dowolnego ![]() Zatem
Zatem ![]() co oznacza, że podrozmaitość
co oznacza, że podrozmaitość ![]() jest styczna w punkcie
jest styczna w punkcie ![]() do przestrzeni
do przestrzeni ![]() ∎
∎
Dowód Twierdzenia 1.18. Połóżmy ![]() czyli
przekształcenie potoku fazowego po czasie
czyli
przekształcenie potoku fazowego po czasie ![]() i niech
i niech ![]() będzie lokalną rozmaitością stabilną dla
będzie lokalną rozmaitością stabilną dla ![]() (patrz
Twierdzenie 1.22). Ponieważ podrozmaitość
(patrz
Twierdzenie 1.22). Ponieważ podrozmaitość ![]() jest
definiowana topologicznie jako zbiór tych punktów
jest
definiowana topologicznie jako zbiór tych punktów ![]() że
że ![]() gdy
gdy ![]() to
to ![]() Z drugiej strony, jeśli
Z drugiej strony, jeśli ![]() , to zapisując
, to zapisując ![]() dla
dla ![]() i
i ![]() mamy
mamy ![]() (jako, że rodzina
(jako, że rodzina ![]() jest jednakowo ciągła). ∎
jest jednakowo ciągła). ∎
Drugi podstawowy wynik dotyczący hiperbolicznych punktów stałych pochodzi od D. Grobmana i P. Hartmana ([13]). Formułujemy go jednocześnie dla kaskad i potoków.
Twierdzenie 1.23 (Grobman–Hartman). Niech ![]() będzie kiełkiem dyfeomorfizmu klasy
będzie kiełkiem dyfeomorfizmu klasy ![]()
![]() z hiperbolicznym punktem stałym w
z hiperbolicznym punktem stałym w ![]() Wtedy
istnieje lokalny homeomorfizm
Wtedy
istnieje lokalny homeomorfizm ![]()
![]() taki, że
taki, że
| (1.27) |
Analogicznie, dla lokalnego potoku ![]() generowanego przez kiełek pola wektorowego
generowanego przez kiełek pola wektorowego ![]() z
hiperbolicznym punktem równowagi
z
hiperbolicznym punktem równowagi ![]() istnieje lokalny
homeomorfizm
istnieje lokalny
homeomorfizm ![]() (jak wyżej) taki, że
(jak wyżej) taki, że
| (1.28) |
Dowód. Zaczniemy od przypadku kaskady. Podobnie jak w przypadku
dowodu Twierdzenia 1.22 sprowadzamy sytuację do przypadku, gdy ![]() i
i
gdzie ![]() zachodzą oszacowania (1.24) i
zachodzą oszacowania (1.24) i ![]() jest określone na całym
jest określone na całym ![]() oraz jest małe wraz z pochodnymi.
Homeomorfizm
oraz jest małe wraz z pochodnymi.
Homeomorfizm ![]() wybierzemy w postaci
wybierzemy w postaci
| (1.29) |
Równanie (1.27) na ![]() które odnacza przemienność następującego diagramu
które odnacza przemienność następującego diagramu
![\begin{array}[]{ccc}\mathbb{R}^{{n}}&\overset{f}{\longmapsto}&\mathbb{R}^{{n}}\\
\uparrow h&&\uparrow h\\
\mathbb{R}^{{n}}&\overset{L}{\longmapsto}&\mathbb{R}^{{n}}\end{array}](wyklady/rrj/mi/mi412.png) |
prowadzi do równania ![]() W składowych dostajemy układ równań
W składowych dostajemy układ równań
Przepiszmy ten układ w dogodnej dla nas formie
| (1.30) |
Łatwo rozpoznać tu równanie punktu stałego ![]() dla nieliniowego operatora
dla nieliniowego operatora ![]() działającego na
działającego na![]() poprzez prawe strony układu (1.30).
poprzez prawe strony układu (1.30).
Jako przestrzeń Banacha wybierzemy
z normą ![]() . Tutaj już nietrudno pokazać, że
operator
. Tutaj już nietrudno pokazać, że
operator ![]() przekształca kulę w
przekształca kulę w ![]() o odpowiednim
promieniu w siebie i że jest kontrakcją. Podstawowy argument polega
na tym, że macierze
o odpowiednim
promieniu w siebie i że jest kontrakcją. Podstawowy argument polega
na tym, że macierze ![]() i
i ![]() mają normę
mają normę ![]() .
.
Oderwijmy się na moment od naszego dowodu i rozważmy sytuację, gdy równanie (1.27) zastąpić równaniem
| (1.31) |
gdzie ![]() Po podstawieniu
Po podstawieniu ![]() i pewnych przekształceniach otrzymujemy następujący analog układu (1.30)
i pewnych przekształceniach otrzymujemy następujący analog układu (1.30)
Tutaj też mamy do czynienia z równaniem punktu stałego dla
odpowiedniego przekształcenia ![]() , które jest zwężające. Zatem również układ
(1.31) ma rozwiązanie.
, które jest zwężające. Zatem również układ
(1.31) ma rozwiązanie.
Odnotujmy następującą własność rozwiązań równań (1.27) i (1.31), które są konsekwencją faktu, że w tezie twierdzenia Banacha o punkcie stałym przekształcenia zwężającego w przestrzeni Banacha tenże punkt stały zależy w sposób ciągły od parametrów (o ile samo przekształcenie zależy od parametrów w sposób ciągły):
Rozwiązania ![]() i
i ![]() równań (1.27) i (1.31) są jednoznaczne i zależą w sposób ciągły od danych występujących w tych równaniach (czyli od
równań (1.27) i (1.31) są jednoznaczne i zależą w sposób ciągły od danych występujących w tych równaniach (czyli od ![]() i
i![]() Ponadto w równaniu (1.27) możemy zastąpić liniowe przekształcenie
Ponadto w równaniu (1.27) możemy zastąpić liniowe przekształcenie ![]() dowolnym przekształceniem
dowolnym przekształceniem ![]() takim,
że
takim,
że![]()
Wyżej wspomniana jednoznaczność pozwoli nam na udowodnienie,
że przekształcenia ![]() i
i ![]() są homeomorfizmami; dokładniej,
że
są homeomorfizmami; dokładniej,
że ![]() Rzeczywiście, przekształcenie
Rzeczywiście, przekształcenie ![]() spełnia warunek
spełnia warunek ![]() czyli równanie
(1.27) dla
czyli równanie
(1.27) dla ![]() Ponieważ również przekształcenie tożsamościowe też spełnia to równanie, to z jednoznaczności mamy
Ponieważ również przekształcenie tożsamościowe też spełnia to równanie, to z jednoznaczności mamy ![]() Analogicznie, przekształcenia
Analogicznie, przekształcenia ![]() i
i ![]() spełniają
równanie
spełniają
równanie ![]()
Przejdźmy teraz do dowodu drugiej części twierdzenia, czyli
isnienia homeomorfizmu ![]() , który spełnia jendocześnie wszystkie równania typu (1.27) dla rodziny przekształceń
, który spełnia jendocześnie wszystkie równania typu (1.27) dla rodziny przekształceń ![]()
![]() . Dla
. Dla ![]() przekształcenia
przekształcenia ![]() mają
hiperboliczny punkt stały
mają
hiperboliczny punkt stały ![]() Zatem z udowodnionej już pierwszej części twierdzenia mamy istnienie rodziny homeomorfizmów
Zatem z udowodnionej już pierwszej części twierdzenia mamy istnienie rodziny homeomorfizmów ![]()
![]() , takich, że
, takich, że
Trzeba jeszcze tylko pokazać, że ![]() nie zależą od
nie zależą od ![]() który tutaj traktujemy jako parametr. Przynajmniej wiemy, że
który tutaj traktujemy jako parametr. Przynajmniej wiemy, że ![]() zależy od
zależy od ![]() w sposób ciągły.
w sposób ciągły.
Zauważmy teraz następującą tożsamość
(tutaj wykorzystaliśmy grupową własność potoku fazowego).
Oznacza ona, że ![]() (jednoznaczność). Analogicznie
dowodzi się, że
(jednoznaczność). Analogicznie
dowodzi się, że ![]() dla naturalnego
dla naturalnego ![]() i stąd,
że
i stąd,
że
(Zadanie 1.41). Widać, że dla wymiernego zbioru parametrów ![]() przekształcenia
przekształcenia ![]() są takie same. Z ciągłej zależności
są takie same. Z ciągłej zależności ![]() of parametru (patrz wyżej) wynika, że
of parametru (patrz wyżej) wynika, że ![]() jako funkcja od
jako funkcja od ![]() Teraz obserwacja, że jeśli
Teraz obserwacja, że jeśli ![]() spełnia równanie (1.28) dla danego czasu
spełnia równanie (1.28) dla danego czasu ![]() to spełnia to równanie też dla czasu
to spełnia to równanie też dla czasu ![]() (Zadanie 1.42) kończy dowód.
(Zadanie 1.42) kończy dowód.
Na koniec jeszcze jedna uwaga. Ponieważ ![]() jest tylko lokalnym potokiem fazowym (dla pola wektorowego
jest tylko lokalnym potokiem fazowym (dla pola wektorowego ![]() określonego w otoczeniu
określonego w otoczeniu ![]() to trzeba zatroszczyć się o dziedziny
przekształceń potoku, i tym samym, o dziedziny przkształceń
to trzeba zatroszczyć się o dziedziny
przekształceń potoku, i tym samym, o dziedziny przkształceń ![]() Ale tu nie ma problemu, bo dziedzina przekształcenia
Ale tu nie ma problemu, bo dziedzina przekształcenia ![]() zwiększa się ze wzrostem
zwiększa się ze wzrostem ![]() Wystarczy w powyższym dowodzie ograniczyć się do czasów takich , że
Wystarczy w powyższym dowodzie ograniczyć się do czasów takich , że ![]() ∎
∎
Własność (1.27) oznacza, że dynamika (tj. kaskada) generowana
przez dyfeomorfizm ![]() jest taka sama, z jakościowego punktu widzenia
jak dynamika generowana przez dyfeomorfizm liniowy
jest taka sama, z jakościowego punktu widzenia
jak dynamika generowana przez dyfeomorfizm liniowy ![]() Rzeczywiście, jeśli
Rzeczywiście, jeśli ![]() jest orbitą
punktu względem dyfeomorfizmu
jest orbitą
punktu względem dyfeomorfizmu ![]() i
i ![]() , to
, to ![]() jest orbitą
punktu
jest orbitą
punktu ![]() względem liniowego dyfeomorfizmu
względem liniowego dyfeomorfizmu ![]()
Następująca definicja wydaje się naturalna.
Definicja 1.24. Jeśli dla dyfeomorfizmów ![]() i
i ![]() istnieje homeomorfizm
istnieje homeomorfizm ![]() taki, że
taki, że
to mówimy, że dyfeomorfizmy ![]() i
i ![]() są topologicznie
sprzężone (przy pomocy
są topologicznie
sprzężone (przy pomocy ![]() Jeśli
Jeśli ![]() jest klasy
jest klasy ![]() ,
to mówimy o sprzężeniu klasy
,
to mówimy o sprzężeniu klasy ![]() Podobnie, pola
wektorowe
Podobnie, pola
wektorowe ![]() i
i ![]() są topologicznie (lub klasy
są topologicznie (lub klasy ![]() sprzężone, jeśli ich potoki fazowe są sprzężone
przy pomocy homeomorfizmu (lub odpowiednio dyfeomorfizmu klasy
sprzężone, jeśli ich potoki fazowe są sprzężone
przy pomocy homeomorfizmu (lub odpowiednio dyfeomorfizmu klasy ![]()
Jeśli dyfeomorfizm ![]() ma własność, że dowolny
dyfeomorfizm
ma własność, że dowolny
dyfeomorfizm ![]() który jest bliski
który jest bliski ![]() (w pewnej klasie, której
tutaj nie chcemy uściślać) jest topologicznie sprzężony
z
(w pewnej klasie, której
tutaj nie chcemy uściślać) jest topologicznie sprzężony
z ![]() to mówimy, że
to mówimy, że ![]() jest strukturalnie stabilny.
Podobnie, pole wektorowe
jest strukturalnie stabilny.
Podobnie, pole wektorowe ![]() jest strukturalnie stabilne jeśli bliskie pola są topologicznie sprzężone z nim.
jest strukturalnie stabilne jeśli bliskie pola są topologicznie sprzężone z nim.
Twierdzenie Grobmana–Hartmana mówi, że dyfeomorfizm (odpowiednio pole wektorowe) w otoczeniu hiperbolicznego punktu stałego (odpowiednio hiperbolicznego punktu równowagi) jest topologicznie sprzężone z częścią liniową dyfeomorfizmu (odpowiednio pola). Możemy udowodnić więcej.
Stwierdzenie 1.25.Dyfeomorfizm (odpowiednio pole wektorowe) w otoczeniu hiperbolicznego punktu stałego (odpowiednio hiperbolicznego punktu równowagi) jest strukturalnie stabilny.
Dowód. Użyjemy następującej bezpośredniej
konstrukcji homeomorfizmu ![]() który sprzęga dwa dyfeomorfizmy
który sprzęga dwa dyfeomorfizmy ![]() i
i ![]() w przypadku asymptotycznie stabilnym, tzn. takim, że
w przypadku asymptotycznie stabilnym, tzn. takim, że ![]() i
i ![]() mają wszystkie wartości własne o module
mają wszystkie wartości własne o module ![]() Można założyć, że
Można założyć, że ![]() i
i ![]() w
dowodzie twierdzenia Grobmana–Hartmana. Wtedy istnieje `funkcja Lapunowa',
w
dowodzie twierdzenia Grobmana–Hartmana. Wtedy istnieje `funkcja Lapunowa', ![]() tzn. spełniająca warunek (i) Definicji 1.5 i następujący
analog warunku (ii):
tzn. spełniająca warunek (i) Definicji 1.5 i następujący
analog warunku (ii):
Jej konstrukcja jest zpełnie analogiczna jak w dowodzie Twierdzenia
Lapunowa; możemy założyć, że ![]() w odpowiednim (liniowym) układzie współrzędnych. Niech
w odpowiednim (liniowym) układzie współrzędnych. Niech ![]() będzie odpowiednią funkcją
Lapunowa dla dyfeomorfizmu
będzie odpowiednią funkcją
Lapunowa dla dyfeomorfizmu ![]() (też w odpowiednim układzie współrzędnych). Mamy dwa egzemplarze
(też w odpowiednim układzie współrzędnych). Mamy dwa egzemplarze ![]() , na których działają odpowiednio dyfeomorfizmy
, na których działają odpowiednio dyfeomorfizmy ![]() i
i ![]()
Wybierzmy małe ![]() i rozważmy hiperpowierzchnie
(dyfeomorficzne ze sferami)
i rozważmy hiperpowierzchnie
(dyfeomorficzne ze sferami) ![]() i
i ![]() Zdefiniujmy homeomorfizm
Zdefiniujmy homeomorfizm ![]() pomiędzy
tymi hiperpowierzchniami jako
pomiędzy
tymi hiperpowierzchniami jako ![]() (patrz Rysunek 1.8). Warunek
(patrz Rysunek 1.8). Warunek
| (1.32) |
pozwala 'dookreślić' przekształcenie ![]() pomiędzy
hiperpowierzchniami
pomiędzy
hiperpowierzchniami![]() i
i ![]() jak na Rysunku 1.8. Przedłużmy
jak na Rysunku 1.8. Przedłużmy ![]() w sposób ciągły i wzajemnie jednoznaczny do
obszaru pomiędzy hiperpowierzchniami
w sposób ciągły i wzajemnie jednoznaczny do
obszaru pomiędzy hiperpowierzchniami ![]() i
i
![]() Stosując
wielokrotnie równanie (1.32) przedłużamy
Stosując
wielokrotnie równanie (1.32) przedłużamy ![]() do całego
obszaru
do całego
obszaru ![]() . Kładąc
. Kładąc ![]() dostajemy poszukiwany homeomorfizm.
dostajemy poszukiwany homeomorfizm.
Zupełnie analogiczna konstrukcja pracuje w przypadku dyfeomorfizmów
rozszerzających, tzn. gdy macierze ![]() i
i ![]() mają wartości własne o module
mają wartości własne o module ![]()
Rozważmy teraz dwa dyfeomorfizmy liniowe ![]() i
i ![]() definiowane
przy pomocy hiperbolicznych macierzy
definiowane
przy pomocy hiperbolicznych macierzy ![]() i
i ![]() w odpowiednich (i takich samych) rozkładach
w odpowiednich (i takich samych) rozkładach ![]() Z powyższych rozważań dostajemy
homeomorfizmy
Z powyższych rozważań dostajemy
homeomorfizmy ![]() i
i ![]() , które sprzęgają
, które sprzęgają ![]() z
z ![]() i
i ![]() z
z ![]() odpowiednio. Teraz homeomorfizm
odpowiednio. Teraz homeomorfizm
sprzęga ![]() z
z ![]()
Rozważmy teraz dyfeomorfizm ![]() w otoczeniu hiperbolicznego punktu stałego
w otoczeniu hiperbolicznego punktu stałego ![]() i jego małe zaburzenie
i jego małe zaburzenie ![]() z tym samym punktem stałym. Ponieważ macierz
z tym samym punktem stałym. Ponieważ macierz ![]() jest bliska macierzy
jest bliska macierzy ![]() to
też jest hiperboliczna z takimi samymi wymiarami podprzestrzeni
stabilnej i niestabilnej; czyli możemy zastosować powyższą
konstrukcję homeomorfizmu sprzęgającego części liniowe
tych dyfeomorfizmów. Widzimy, że
to
też jest hiperboliczna z takimi samymi wymiarami podprzestrzeni
stabilnej i niestabilnej; czyli możemy zastosować powyższą
konstrukcję homeomorfizmu sprzęgającego części liniowe
tych dyfeomorfizmów. Widzimy, że ![]() jest sprzężony z
jest sprzężony z ![]() ,
, ![]() jest sprzężony z
jest sprzężony z ![]() i
i ![]() jest sprzęzony z
jest sprzęzony z ![]() składając te trzy
homeomorfizmy dostaje się sprzężenie
składając te trzy
homeomorfizmy dostaje się sprzężenie ![]() z
z ![]()
Przypadek Stwierdzenia 1.25 dla pól wektorowych pozostawiamy słucha- czom jako ćwiczenie (Zadanie 1.43). ∎
Uwaga 1.26. Można zapytać, czy nie można wzmocnić
tezy twierdzenia Grobmana-Hartmana, tzn. czy homeomorfizm ![]() może być klasy
może być klasy ![]() Okazuje się, że nie. Na przykład, przekształcenie
Okazuje się, że nie. Na przykład, przekształcenie ![]() nie da się zlinearyzować przy pomocy
dyfeomorfizmu klasy
nie da się zlinearyzować przy pomocy
dyfeomorfizmu klasy ![]() (patrz [13], Problem 8.1). Ten problem wiąże się z rezonansami pomiędzy wartościami własnymi (patrz
Twierdzenie Poincarégo–Dulaca w Rozdziale 3.3).
(patrz [13], Problem 8.1). Ten problem wiąże się z rezonansami pomiędzy wartościami własnymi (patrz
Twierdzenie Poincarégo–Dulaca w Rozdziale 3.3).
ZADANIA
Zadanie 1.27. Uzupełnić dowód Lematu 1.7, tzn. w przypadku nierzeczywistych wartości własnych.
Zadanie 1.28. Udowodnić wzory (1.11)–(1.15).
Zadanie 1.29. Zbadać stabilność (w sensie Lapunowa i
asymptotyczną) dla punktu osobliwego ![]()
![]() układu
Lotki–Volterry
układu
Lotki–Volterry
| (1.33) |
który opisuje dynamikę dwóch konkurujących populacji (drapieżników i ofiar).
Wskazówka: Stwierdzenie 2.11 poniżej.
Zadanie 1.30. Korzystając z Definicji 1.1 sprawdzić, czy położenie równowagi ![]() dla równania
dla równania ![]() jest stabilne w sensie Lapunowa, t.j. z
jest stabilne w sensie Lapunowa, t.j. z ![]() .
.
Zadanie 1.31. Zbadać stabilność położenia równowagi ![]() dla układu
dla układu ![]()
![]()
Zadanie 1.32. Zbadać stabilność zerowego rozwiązania dla układu ![]()
![]()
![]()
Zadanie 1.33. Dla jakich wartości parametru ![]() rozwiązanie zerowe układu
rozwiązanie zerowe układu ![]()
![]() jest
asymptotycznie stabilne?
jest
asymptotycznie stabilne?
Wskazówka: gdy![]() prosta
prosta ![]() jest niezmiennicza.
jest niezmiennicza.
Zadanie 1.34. Dla jakich wartości parametrów ![]() i
i ![]() rozwiązanie zerowe układu
rozwiązanie zerowe układu ![]()
![]() jest
asymptotycznie stabilne?
jest
asymptotycznie stabilne?
Wskazówka: dla ![]() wprowadzając
wprowadzając ![]() sprowadzić
układ do postaci
sprowadzić
układ do postaci ![]()
![]()
![]() i znaleźć funkcję Lapunowa.
i znaleźć funkcję Lapunowa.
Zadanie 1.35. Dla jakich wartości parametrów ![]() i
i ![]() rozwiązanie
rozwiązanie ![]() równania
równania ![]() jest asymptotycznie stabilne?
jest asymptotycznie stabilne?
Zadanie 1.36. Pokazać, że dyfeomorfizm ![]() (lokalnego)
potoku fazowego generowanego przez pole wektorowe
(lokalnego)
potoku fazowego generowanego przez pole wektorowe ![]() ma część liniową w punkcie stałym
ma część liniową w punkcie stałym ![]() postaci
postaci ![]() Wywnioskować stąd Lemat 1.21.
Wywnioskować stąd Lemat 1.21.
Zadanie 1.37. Udowodnić oszacowania (1.24) (dla odpowiedniego
układu współrzędnych i euklidesowej normy w ![]()
Zadanie 1.38. Podać jawny wzór na funkcję ![]() z
dowodu Twierdzenia 1.22.
z
dowodu Twierdzenia 1.22.
Zadanie 1.39. Udowodnić nierówność dla ![]() z dowodu Twierdzenia
1.22.
z dowodu Twierdzenia
1.22.
Zadanie 1.40. Podać jakiś wzór na ![]() , w zależności od
, w zależności od ![]() , w nierówności
, w nierówności ![]() .
.
Zadanie 1.41. Udowodnić, że ![]() dla
dla ![]() i
i ![]()
Zadanie 1.42. Udowodnić, że jeśli ![]() spełnia własność (1.28) dla danego
spełnia własność (1.28) dla danego ![]() to też spełnia tę własność dla
to też spełnia tę własność dla ![]()
Zadanie 1.43. Uzupełnić dowód Stwierdzenia 1.25.