Zagadnienia
4. Równania z małym parametrem
Mały parametr w równaniu różniczkowym może pojawiać się zasadniczo na dwa sposoby: albo z prawej strony albo z lewej strony. W pierwszym przypadku mamy do czynienia z małym zaburzeniem układu, o którym na ogół sporo wiemy a w drugim przypadku pojawiają się tzw. drgania relaksacyjne. Oba przypadki są omawiane kolejno w następnych rozdziałach.
4.1. Uśrednianie
Przykładem układu z pierwszej grupy jest znany układ van der Pola
gdzie ![]() jest naszym małym parametrem. Jest to szczególny
przypadek zaburzenia układu hamiltonowskiego o jednym stopniu
swobody
jest naszym małym parametrem. Jest to szczególny
przypadek zaburzenia układu hamiltonowskiego o jednym stopniu
swobody
| (4.1) |
W zastosowaniach często pojawiają się układy hamiltonowskie z wieloma stopniami swobody postaci
| (4.2) |
gdzie ![]() jest funkcją
Hamiltona, lub hamiltonianem (Zadania 4.11 i 4.12). Na
ogół układ (4.2) nie daje się rozwiązać. Jednak istnieje
klasa układów hamiltonowkich w pełni rozwiązywalnych.
jest funkcją
Hamiltona, lub hamiltonianem (Zadania 4.11 i 4.12). Na
ogół układ (4.2) nie daje się rozwiązać. Jednak istnieje
klasa układów hamiltonowkich w pełni rozwiązywalnych.
Definicja 4.1. Układ (4.2) nazywa się zupełnie całkowalnym jeśli istnieje układ funkcjonalnie niezależnych całek
pierwszych ![]()
![]()
![]() taki, że każda
funkcja
taki, że każda
funkcja ![]() jest całką pierwszą dla innych układów
hamiltonowskich generowanych przez inne funkcje
jest całką pierwszą dla innych układów
hamiltonowskich generowanych przez inne funkcje ![]() Mówi się
też, że funkcje
Mówi się
też, że funkcje ![]() są w inwolucji.
są w inwolucji.
Przykładami układów zupełnie całkowalnych jest zagadnienie Keplera i potok geodezyjny na powierzchni elipsoidy (patrz [4]); oba mają dwa stopnie swobody.
Dla układów spełniających warunek z Definicji 4.1 zachodzi następujące twierdzenie, które przytaczamy bez dowodu (patrz [4]).
Twierdzenie 4.2 (Liouville–Arnold). Jeśli wspólne
poziomice ![]()
![]() zupełnie całkowalnego układu hamiltonowskiego są zwarte i gładkie, to są one
torusami
zupełnie całkowalnego układu hamiltonowskiego są zwarte i gładkie, to są one
torusami ![]()
Ponadto w otoczeniu danego takiego torusa istnieje układ współrzędnych ![]() , tzw. zmienne działanie–kąt, w których układ (4.2) przyjmuje następującą postać hamiltonowską
, tzw. zmienne działanie–kąt, w których układ (4.2) przyjmuje następującą postać hamiltonowską
| (4.3) |
gdzie ![]() jest
hamiltonianem po zamianie. W szczgólności ruch na torusach
jest
hamiltonianem po zamianie. W szczgólności ruch na torusach ![]() , które są
parametryzowane przez kąty
, które są
parametryzowane przez kąty ![]() mod
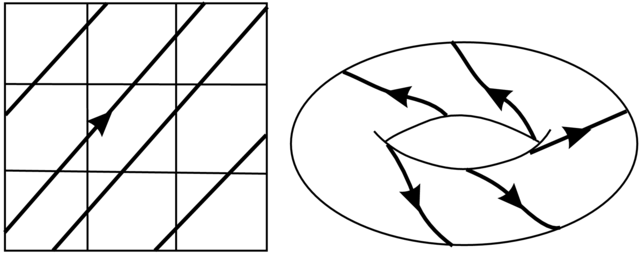
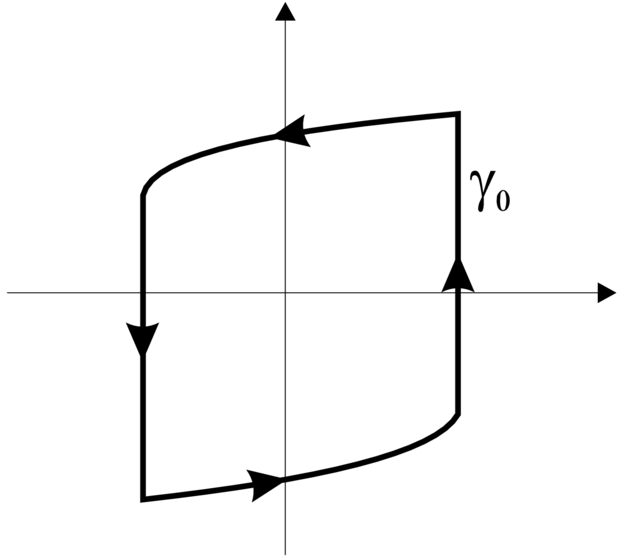
mod ![]() jest okresowy lub prawie-okresowy (patrz Rysunek 4.1):
jest okresowy lub prawie-okresowy (patrz Rysunek 4.1):
Przykład 4.3. Dla układu van der Pola z ![]() i
i ![]() zmienne działanie–kąt są następujące:
zmienne działanie–kąt są następujące: ![]() i
i ![]()
Rozważmy teraz następujące zaburzenie układu (4.3)
| (4.4) |
gdzie ![]()
![]() and
and ![]() . Naturalne jest spodziewać się, że rozwiązanie układu (4.4)
po czasie rzędu
. Naturalne jest spodziewać się, że rozwiązanie układu (4.4)
po czasie rzędu ![]() różni sę od rozwiązania układu
(4.3) z tymi samymi warunkami początkowymi o wielkość rzędu
różni sę od rozwiązania układu
(4.3) z tymi samymi warunkami początkowymi o wielkość rzędu
![]() Tymczasem poniższe Twierdzenie 4.4 mówi, że
taką samą wielkość
Tymczasem poniższe Twierdzenie 4.4 mówi, że
taką samą wielkość ![]() można uzyskać
po czasie dążącym do nieskończoności przy
można uzyskać
po czasie dążącym do nieskończoności przy ![]() Tego rodzaju zjawisko ma miejsce dzięki tzw. uśrednieniu.
Tego rodzaju zjawisko ma miejsce dzięki tzw. uśrednieniu.
Idea uśrednienia wiąże się z faktem, że na większości torusów ![]() trajektori układu niezaburzonego jest gęsta (jak na Rysunku 4.1).
Zatem średnie odchylenie działania
trajektori układu niezaburzonego jest gęsta (jak na Rysunku 4.1).
Zatem średnie odchylenie działania ![]() można wyliczyć (w
przybliżeniu) poprzez uśrednienie po torusie.
można wyliczyć (w
przybliżeniu) poprzez uśrednienie po torusie.
Definijemy układ uśredniony
| (4.5) |
gdzie
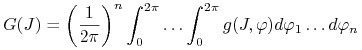 |
jest uśrednioną po ![]() wielkością prędkości zmian działania.
wielkością prędkości zmian działania.
Twierdzenie 4.4 (O uśrednianiu). Niech ![]() i funkcje
i funkcje ![]() będą klasy
będą klasy ![]() i
i ![]() na otwartym podzbiorze
na otwartym podzbiorze ![]() Jeśli
Jeśli ![]() i
i ![]() są rozwiązaniami układów (4.4) i (4.5) takimi, że
są rozwiązaniami układów (4.4) i (4.5) takimi, że ![]() to dla
to dla
amy
gdzie stała ![]() zależy tylko od
zależy tylko od![]()
Dowód. Dokonajmy zamiany
| (4.6) |
tak, aby zachodziło ![]() Wyliczenie
Wyliczenie ![]() przebiega następująco
przebiega następująco
![\begin{array}[]{lll}\dot{K}&=&\dot{I}+\varepsilon\frac{\partial k}{\partial I}\dot{I}+\varepsilon\frac{\partial k}{\partial\varphi}\dot{\varphi}=\varepsilon\left\{ g+\frac{\partial k}{\partial\varphi}\omega\right\}+O(\varepsilon^{{2}})\\
&=&\varepsilon\left\{ g(K,\varphi)+\frac{\partial k}{\partial\varphi}(K,\varphi)\omega(K)\right\}+O(\varepsilon^{{2}}).\end{array}](wyklady/rrj/mi/mi1821.png) |
Zatem chcemy rozwiązać równanie
z oczywistym rozwiązaniem ![]() Niestety, na ogół to rozwiązanie nie jest jednoznaczną (czyli okresową) funkcją od
Niestety, na ogół to rozwiązanie nie jest jednoznaczną (czyli okresową) funkcją od ![]() Przeszkodą jest wielkość
Przeszkodą jest wielkość ![]() która może być niezerowa.
która może być niezerowa.
Ale, zapisując
tak, że ![]() możemy
zdefiniować jednoznaczną funkcję
możemy
zdefiniować jednoznaczną funkcję
Dostajemy równanie
Widać, że po czasie ![]() różnica pomiędzy
różnica pomiędzy
![]() i
i ![]() jest rzędu
jest rzędu ![]() Z drugiej strony, różnica pomiędzy
Z drugiej strony, różnica pomiędzy ![]() i
i ![]() jest rzędu
jest rzędu ![]() dzięki zamianie (4.6). ∎
dzięki zamianie (4.6). ∎
Dla zaburzeń typu (4.4) zupełnie całkowalnych układów
hamiltonoskich z wieloma stopniami swobody oszacowania są słabsze niż w tezie Twierdzenia 4.4. Okazuje się, że po czasie czędu ![]() , dla warunków początkowych spoza zbioru o
mierze Lebesque's
, dla warunków początkowych spoza zbioru o
mierze Lebesque's ![]() odchylenie
odchylenie ![]() od
od ![]() nie
przekracza
nie
przekracza ![]() gdzie
gdzie ![]() są wykładnikami
zależnymi od
są wykładnikami
zależnymi od ![]() Po więcej informacji odsyłam
czytelnika do [5].
Po więcej informacji odsyłam
czytelnika do [5].
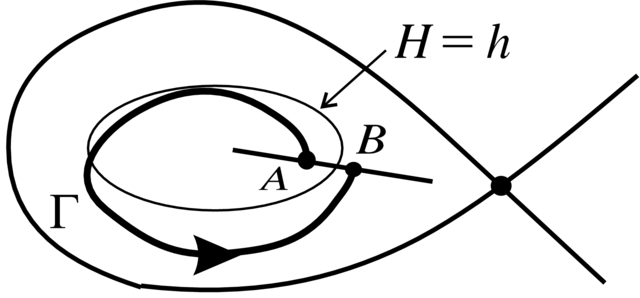
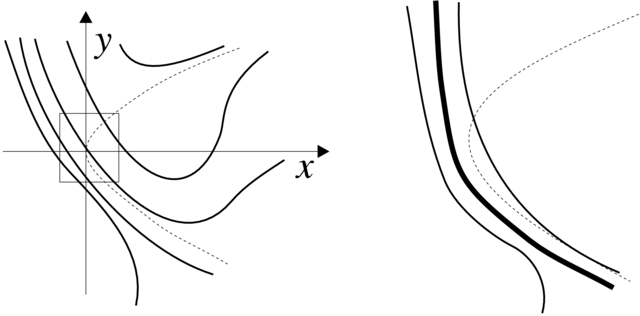
Przykład 4.5 (Całki abelowe). Rozważmy następujące zaburzenie dwuwymiarowego układu hamiltonowskiego
Dla ![]() krzywe fazowe leżą w poziomicach funkcji
Hamiktona
krzywe fazowe leżą w poziomicach funkcji
Hamiktona ![]() W pewnym obszarze przestrzeni fazowej te krzywe są
zamknięte. Jak już robiliśmy to kilkakrotnie, badanie cykli
granicznych układu zaburzonego polega na analizie przekształcenia
powrotu Poincarégo z
W pewnym obszarze przestrzeni fazowej te krzywe są
zamknięte. Jak już robiliśmy to kilkakrotnie, badanie cykli
granicznych układu zaburzonego polega na analizie przekształcenia
powrotu Poincarégo z![]() (cięcie transweralne do krzywych
fazowych) do
(cięcie transweralne do krzywych
fazowych) do ![]() Parametryzując
Parametryzując ![]() za pomocą
za pomocą ![]() warunek
cyklu granicznego to
warunek
cyklu granicznego to ![]() (patrz Rysunek 4.2). Mamy
(patrz Rysunek 4.2). Mamy
![\begin{array}[]{lll}\Delta H&=&\int _{{0}}^{{T}}\frac{dH}{dt}dt=\int _{{0}}^{{T}}\left\{ H_{{x}}^{{\prime}}\left(H_{{y}}^{{\prime}}+\varepsilon P\right)+H_{{y}}^{{\prime}}(-H_{{x}}^{{\prime}}+\varepsilon Q\right\} dt\\
&=&\varepsilon\int\left(PH^{{\prime}}x+QH_{{y}}^{{\prime}}\right)dt=\varepsilon\int\left\{ P(H_{{x}}^{{\prime}}-\varepsilon Q)+Q\left(H_{{y}}^{{\prime}}+\varepsilon P\right)\right\}\\
&=&\varepsilon\int _{{\Gamma(h)}}Qdx-Pdy=\varepsilon\oint _{{H=h}}\left(Qdx-Pdy\right)+O(\varepsilon^{{2}}),\end{array}](wyklady/rrj/mi/mi1601.png) |
gdzie ![]() jest czasem powrotu do
jest czasem powrotu do ![]() a
a ![]() jest krzywą fazową układu zaburzonego startującą z
jest krzywą fazową układu zaburzonego startującą z ![]() takiego, że
takiego, że ![]()
Wyrażenie
| (4.7) |
jest tzw. całką abelową.15Pojęcie całki abelowej wywodzi się z zespolonej geometrii
algebraicznej. Są to całki z ![]() form meromorficznych wzdłuż
pewnych zamkniętych krzywych na zespolonych krzywych algebraicznych
(powierzchniach Riemanna). Gdy
form meromorficznych wzdłuż
pewnych zamkniętych krzywych na zespolonych krzywych algebraicznych
(powierzchniach Riemanna). Gdy ![]()
![]() i
i ![]() są
wielomianami, to powierzchnia Riemanna jest zespoloną krzywą
są
wielomianami, to powierzchnia Riemanna jest zespoloną krzywą ![]() a
a ![]() forma to
forma to ![]() Z Twierdzenia o funkcjach uwikłanych
wynika, że jeśli
Z Twierdzenia o funkcjach uwikłanych
wynika, że jeśli ![]() i
i ![]() to dla
to dla ![]() i małego istnieje cykl graniczny
i małego istnieje cykl graniczny ![]() który dąży do krzywej
który dąży do krzywej ![]() przy
przy ![]() To podejście do problemu cykli granicznych
jest szeroko stosowane w Jakościowej Teorii.
To podejście do problemu cykli granicznych
jest szeroko stosowane w Jakościowej Teorii.
Nietrudno zauważyć, że funkcja ![]() jest odpowiednikiem całki uśrednienia
jest odpowiednikiem całki uśrednienia ![]() która występuje we wzorze (4.5).
która występuje we wzorze (4.5).
4.2. Teoria KAM
Rozważmy układ hamiltonowski
![]()
![]() z hamiltonianem postaci
z hamiltonianem postaci
gdzie ![]() jest hamiltonianem układu zupełnie całkowalnego, czyli
układu typu (4.3) w zmiennych działanie–kąt. Z tą sytuacją
wiąże się jedno z najważniejszych twierdzeń
matematycznych drugiej połowy XX wieku. Przed jego sformułowaniem musimy
wprowadzić jeszcze dwa założenia dotyczące niezdegenerowania
niezaburzonego hamiltonianu
jest hamiltonianem układu zupełnie całkowalnego, czyli
układu typu (4.3) w zmiennych działanie–kąt. Z tą sytuacją
wiąże się jedno z najważniejszych twierdzeń
matematycznych drugiej połowy XX wieku. Przed jego sformułowaniem musimy
wprowadzić jeszcze dwa założenia dotyczące niezdegenerowania
niezaburzonego hamiltonianu ![]()
| (4.8) |
![\det\left[\begin{array}[]{ll}\frac{\partial^{{2}}H_{{0}}}{\partial I_{{i}}\partial I_{{j}}}&\frac{\partial H_{{0}}}{\partial I_{{i}}}\\
\frac{\partial H_{{0}}}{\partial I_{{j}}}&0\end{array}\right].](wyklady/rrj/mi/mi1676.png) |
(4.9) |
Warunek (4.8) oznacza, że częstości ![]() znieniają się niezależnie i dosyć szybko wraz ze zmianą działań
znieniają się niezależnie i dosyć szybko wraz ze zmianą działań ![]() natomiast warunek (4.9) oznacza, że te częstości
zmianiają się szybko i w miarę niezależnie po ograniczeniu
do poziomic
natomiast warunek (4.9) oznacza, że te częstości
zmianiają się szybko i w miarę niezależnie po ograniczeniu
do poziomic ![]()
Twierdzenie 4.6 (Kołmogorow–Arnold–Moser). Jeśli są spełnione warunki niezdegenerowania (4.8) i (4.9) dla ![]() , to dla małego zaburzenia
, to dla małego zaburzenia ![]() większość torusów niezmienniczych
większość torusów niezmienniczych ![]() nie znika, ale tylko lekko deformuje się i ruch na nich jest
dalej prawie okresowy.
nie znika, ale tylko lekko deformuje się i ruch na nich jest
dalej prawie okresowy.
To twierdzenie zostało sformułowane w 1954 roku na Międzynarodowym
Kongresie Matematyków w Amsterdamie, ale na ścisły dowód musiało czekać do początku lat sześdziesiątych. Podali go
niezależnie V. Arnold (w przypadku analitycznym) i J. Moser (w przypadku
gładkim klasy ![]() Później klasa gladkości została obniżona do
Później klasa gladkości została obniżona do ![]() Oczywiście nie jestem w stanie przedstawić tego
dowodu tutaj.
Oczywiście nie jestem w stanie przedstawić tego
dowodu tutaj.
Przykład 4.7. (Płaski ograniczony problem trzech ciał)
Płaskie ograniczone zagadnienie trzech ciał jest to układ w
którym dwa ciała (oddziałujące na siebie siłą
grawitacji) obracają się za stała prędkością kątową wokół ich środka masy (w początku układu współrzędnych) a trzecie ciało porusza się w płaszczyźnie obrotu
dwu ciał i ma masę tak małą, że nie zakłóca ich ruchu.
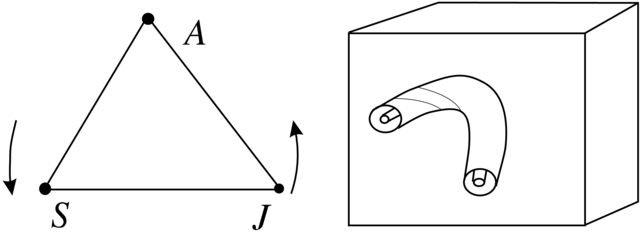
Na Rysunku 4.3 mamy taki układ, w którym ![]() oznacza Słońce,
oznacza Słońce,
![]() -Jowisz,
-Jowisz, ![]() zaś jest Asteroidem. Jednostki czasu, długości i masy można dobrać tak, aby prędkość kątowa, suma mas
zaś jest Asteroidem. Jednostki czasu, długości i masy można dobrać tak, aby prędkość kątowa, suma mas ![]() i
i ![]() oraz stała grawitacyjna były równe
1. Wtedy też odległość między
oraz stała grawitacyjna były równe
1. Wtedy też odległość między ![]() i
i ![]() też równa się
też równa się ![]() Jedynym parametrem charakteryzującym układ jest masa Jowisza
Jedynym parametrem charakteryzującym układ jest masa Jowisza ![]()
Równania ruchu Asteroidu są hamiltonowskie z hamiltonianem
gdzie ![]() i
i ![]() są odległościami
są odległościami ![]() od
od ![]() i
i ![]() odpowiednio. Zauważmy, że położenia
odpowiednio. Zauważmy, że położenia ![]() i
i ![]() zmieniają się z czasem:
zmieniają się z czasem: ![]()
![]() zatem hamiltoniam zależy bezpośredno od czasu.
zatem hamiltoniam zależy bezpośredno od czasu.
Aby pozbyć się tej zależności od czasu, dokonujemy następującej zamiany (jednoczesny obrót współrzędnych i pędów)
Okazuje się, że w nowych zmiennych układ nadal jest hamiltonowski z nowym hamiltonianem
| (4.10) |
![]()
![]() (Zadanie 4.13). W nowych zmiennych
(Zadanie 4.13). W nowych zmiennych ![]() ciała
ciała![]() i
i ![]() spoczywają.
spoczywają.
Punkty równowagi układu hamiltonowsiego to punkty krytyczne funkcji hamiltona (Zadanie 4.14). W przypadku hamiltonianu (4.10) te punkty, które nazywamy względnymi położeniami równowagi, zadane są przez
Mamy
Mamy dwie możliwości:
1. ![]() tutaj znajdujemy trzy punkty tzw. współliniowe punkty libracji
tutaj znajdujemy trzy punkty tzw. współliniowe punkty libracji ![]()
![]()
![]() (Zadanie 4.15), które okazują się niestabilne.
(Zadanie 4.15), które okazują się niestabilne.
2. ![]() i
i ![]() tutaj mamy dwa tzw. trójkątne punkty libracji
tutaj mamy dwa tzw. trójkątne punkty libracji ![]() i
i ![]() które leżą
w wierzchołkach dwóch trójkątów równobocznych o
podstawie
które leżą
w wierzchołkach dwóch trójkątów równobocznych o
podstawie ![]()
Wyliczenia, których nie przeprowadzamy, pokazują, że dla ![]() punkty
punkty ![]() są niestabilne natomiast w przeciwnym
przypadku, tj. dla
są niestabilne natomiast w przeciwnym
przypadku, tj. dla ![]() wartości własne części liniowej układu
hamiltonowskiego są postaci
wartości własne części liniowej układu
hamiltonowskiego są postaci ![]()
![]() gdzie
gdzie ![]() Jesteśmy na granicy
obszaru stabilności.
Jesteśmy na granicy
obszaru stabilności.
Ponadto część kwadratowa ![]() w punkcie
w punkcie ![]() przyjmuje postać
przyjmuje postać
w odpowiednim układzie wspólrzędnych w otoczeniu ![]() (patrz
[19]). Jest to Hamiltonian układu zupełnie całkowalnego ze zmiannymi
działanie–kąt
(patrz
[19]). Jest to Hamiltonian układu zupełnie całkowalnego ze zmiannymi
działanie–kąt ![]()
![]()
![]()
![]() i z
i z ![]() (Zadanie
4.16).
(Zadanie
4.16).
Mamy sytuację jak w Twierdzeniu KAM: ![]() gdzie
gdzie ![]() jest
zupełnie całkowalny a
jest
zupełnie całkowalny a ![]() zawiera wyrazy rzędu
zawiera wyrazy rzędu ![]() ze względu na
ze względu na ![]() (które są małe). Niestety, to nie wystarcza, ponieważ częstości
(które są małe). Niestety, to nie wystarcza, ponieważ częstości ![]() są
stałe, a z warunku niezdegenerowania (4.8) powinny się zmianiać
wraz z
są
stałe, a z warunku niezdegenerowania (4.8) powinny się zmianiać
wraz z ![]() . Należy więc uwzględnić jeszcze dalsze wyrazy
rozwinięcia
. Należy więc uwzględnić jeszcze dalsze wyrazy
rozwinięcia ![]() w otoczeniu
w otoczeniu ![]()
Dokładniej, dokonujemy uproszczenia wyrazów rzędu trzeciego i
czwartego w hamiltonianie ![]() To uproszczenie jest analogiem formy
normalnej Poincarégo–Dulaca i zostało udowodnione przez G.
Birkhoffa w Twierdzeniu 4.9 poniżej. Ta forma normalna Birkhoffa w naszym przypadku ma następującą postać
To uproszczenie jest analogiem formy
normalnej Poincarégo–Dulaca i zostało udowodnione przez G.
Birkhoffa w Twierdzeniu 4.9 poniżej. Ta forma normalna Birkhoffa w naszym przypadku ma następującą postać
| (4.11) |
gdzie ![]()
![]() są
nowymi zmiennymi a
są
nowymi zmiennymi a ![]() zawiera wyrazy rzędu
zawiera wyrazy rzędu ![]() (oraz
(oraz ![]() i
i ![]() są inne niż powyżej). W założeniu twierdzenia
Birkhoffa pojawia się warunek braku relacji rezonansowych rzędu 4 i
3. Okazuje się, że takie relacje zachodzą dla wartości
są inne niż powyżej). W założeniu twierdzenia
Birkhoffa pojawia się warunek braku relacji rezonansowych rzędu 4 i
3. Okazuje się, że takie relacje zachodzą dla wartości ![]() i
i ![]() zatem te wartości parametru
zatem te wartości parametru ![]() należy wykluczyć.
należy wykluczyć.
Hamiltonian ![]() jest hamiltonianem zupełnie całkowalnym i ma szansę na spełnienie warunków niezdegenerowania
(4.8) i (4.9). Okazuje się, że tylko warunek (4.9) jest istotny. A.
Leontowicz pokazał, że może on zostać naruszony tylko dla
dyskretnego zbioru wartości parametru
jest hamiltonianem zupełnie całkowalnym i ma szansę na spełnienie warunków niezdegenerowania
(4.8) i (4.9). Okazuje się, że tylko warunek (4.9) jest istotny. A.
Leontowicz pokazał, że może on zostać naruszony tylko dla
dyskretnego zbioru wartości parametru ![]() Załóżmy zatem, że
Załóżmy zatem, że ![]() spełnia wszystkie warunki wypisane powyżej, czyli jest prawdziwa teza twierdzenia KAM.
spełnia wszystkie warunki wypisane powyżej, czyli jest prawdziwa teza twierdzenia KAM.
Jak z twierdzenia KAM wynika stabilność? Otóż znajdujemy się w przestrzeni ![]() wymiarowej w otoczeniu punktu równowagi.
Ponieważ układ jest hamiltonowski z hamiltonianem niezależnym od
czasu, więc ruch odbywa się po powierzchniach
wymiarowej w otoczeniu punktu równowagi.
Ponieważ układ jest hamiltonowski z hamiltonianem niezależnym od
czasu, więc ruch odbywa się po powierzchniach ![]() Są one trójwymiarowe. Z twierdzenia KAM wynika, że każda taka
powierzchnia jest prawie zapełniona torusami niezmienniczymi
Są one trójwymiarowe. Z twierdzenia KAM wynika, że każda taka
powierzchnia jest prawie zapełniona torusami niezmienniczymi ![]() , których jest tym więcej im bliżej jesteśmy torusa
, których jest tym więcej im bliżej jesteśmy torusa ![]() . Każdy torus niezmienniczy rozbija powierzchnię
. Każdy torus niezmienniczy rozbija powierzchnię ![]() const na dwie części, swoje wnętrze i zewnętrze. Zaden punkt
z wnętrza nie wychodzi zeń w trakcie ewolucji. Ponieważ w
przestrzeni zmiennych
const na dwie części, swoje wnętrze i zewnętrze. Zaden punkt
z wnętrza nie wychodzi zeń w trakcie ewolucji. Ponieważ w
przestrzeni zmiennych ![]() torusy mogą być dowolnie małe, to
wynika stąd stabilność w sensie Lapunowa.
torusy mogą być dowolnie małe, to
wynika stąd stabilność w sensie Lapunowa.
Uzupełnimy powyższy przykład. Załóżmy, że mamy hamiltonian w postaci
Definicja 4.8. Mówimy, że `częstości' ![]() spełniają relację resonansową rzędu
spełniają relację resonansową rzędu ![]() jeśli isnieją liczby całkowite
jeśli isnieją liczby całkowite ![]() z
z ![]() takie, że
takie, że
Twierdzenie 4.9 (Birkhoff). Jeśli częstości ![]() nie spełniają żadnej relacji rezonansowej rzędu
nie spełniają żadnej relacji rezonansowej rzędu ![]() to istnieje kanoniczna zamiana zmiennych
to istnieje kanoniczna zamiana zmiennych ![]() prowadząca do hamiltonianu
prowadząca do hamiltonianu
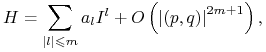 |
gdzie ![]() i
sumowanie przebiega po wielowskaźmikach
i
sumowanie przebiega po wielowskaźmikach ![]() z
z ![]() i
i![]()
Uwaga 4.10. Zamiana ![]() występująca w powyższym twierdzeniu jest kanoniczna jeśli
występująca w powyższym twierdzeniu jest kanoniczna jeśli
Okazuje się, że po kanonicznej zamianie zmiennych układ hamiltonowski przechodzi w układ hamiltonowski (patrz [4]).
ZADANIA
Zadanie 4.11. Pokazać, że jeśli funkcja hamiltona ![]() nie zależy bezpośrednio od czasu, to jest całką pierwszą
dla układu (4.2).
nie zależy bezpośrednio od czasu, to jest całką pierwszą
dla układu (4.2).
Zadanie 4.12. Pokazać, że pole wektorowe zadane wzorem (4.2) ma zerową dywergencję. Wywnioskować stąd, że odpowiedni potok fazowy zachowuje objętość.
Zadanie 4.13. Udowodnić wzór (4.10).
Zadanie 4.14. Pokazać, że jeśli ![]() nie zależy bezpośrednio od czasu, to punkty równowagi układu (4.2) są dokładnie punktami krytycznymi funkcji
nie zależy bezpośrednio od czasu, to punkty równowagi układu (4.2) są dokładnie punktami krytycznymi funkcji ![]()
Zadanie 4.15. Pokazać, że istnieją dokładnie trzy współliniowe punkty libracji.
Zadanie 4.16. Pokazać, że hamiltonian postaci ![]() (lub jak we wzorze (4.11)) jest hamiltonianem układu zupełnie całkowalnego.
(lub jak we wzorze (4.11)) jest hamiltonianem układu zupełnie całkowalnego.
Zadanie 4.17. Zastosować metodę całek abelowych (Przykład 4.5) do pokazania, że układ van der Pola ![]()
![]() dla małego parametru
dla małego parametru ![]() posiada dokładnie jeden cykl
graniczny.
posiada dokładnie jeden cykl
graniczny.
4.3. Drgania relaksacyjne
Zacznijmy od znanego przykładu.
Przykład 4.18 (Układ van der Pola).
(Gdy ![]() i położyć
i położyć ![]() , to dostaje się
, to dostaje się ![]()
![]() z dokładnością do przeskalowania jest to układ z Przykładu 2.34.)
z dokładnością do przeskalowania jest to układ z Przykładu 2.34.)
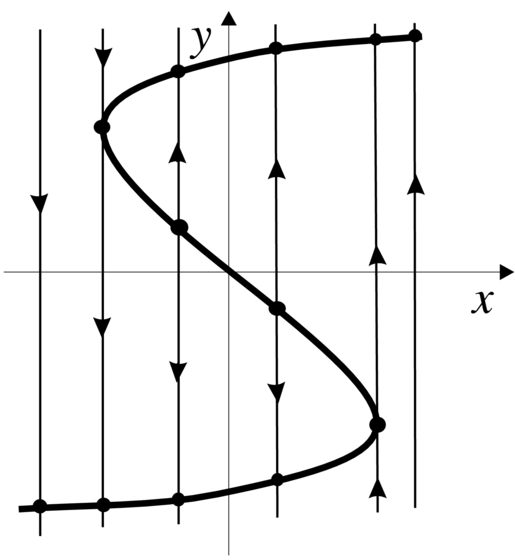
Widać, że ![]() zmienia się szybko w porównaniu z
zmienia się szybko w porównaniu z ![]() mówimy, że
mówimy, że ![]() jest szybką zmienną a
jest szybką zmienną a ![]() wolną. Dla
wolną. Dla ![]() mamy
mamy ![]() const i w istocie mamy równanie na
const i w istocie mamy równanie na
![]() zależne od parametru
zależne od parametru ![]() (teoria bifurkacji się kłania, patrz
Rysunek 4.4). Gdy
(teoria bifurkacji się kłania, patrz
Rysunek 4.4). Gdy ![]() (ale małe), to fizycy
powiedzieliby, że parametr
(ale małe), to fizycy
powiedzieliby, że parametr ![]() `płynie'. Oczekuje się istnienia
cyklu granicznego
`płynie'. Oczekuje się istnienia
cyklu granicznego ![]() (w istocie
(w istocie ![]() jest stabilny) dążącego do kawałkmi gładkiej krzywej
jest stabilny) dążącego do kawałkmi gładkiej krzywej ![]() przedstawionej na Rysunku 4.5. Cykl
przedstawionej na Rysunku 4.5. Cykl ![]() składa się z:
składa się z:
— kawałków ruchu powolnego wzdłuż krzywej ![]() (gdzie
(gdzie ![]()
— odcinków skoku wzdłuż prostych ![]() const.
const.
Taki ruch jest przykładem dragań relaksacyjnych (jak bicie serca).
Rozważmy teraz ogólną sytuację. Mamy układ niezaburzony
(![]() ,
, ![]() ); tutaj
); tutaj ![]() to szybkie współrzędne a
to szybkie współrzędne a ![]() to wolne współrzędne. Mamy też układ zaburzony
to wolne współrzędne. Mamy też układ zaburzony
Definicja 4.19. Powierzchnia ![]() nazywa
się powolną powierzchnią.
nazywa
się powolną powierzchnią.
Powolna powierzchnia dzieli się na obszary stabilności i niestabilności układu niezaburzonego; odpowiadają one sytuacjom gdy ![]() ,
, ![]()
![]() i gdy istnieje
i gdy istnieje ![]()
Na powolnej powierzchni mamy pole wektorowe definiowane następująco. Bierzemy pole
w punkcie ![]() i rzutujemy je na
i rzutujemy je na ![]() wzdłuż zmiennych
wzdłuż zmiennych ![]() Jest to pole ruchu powolnego.
Jest to pole ruchu powolnego.
Przypomnę, że na początku tego rozdziału mówiliśmy,
że drgania relaksacyjne charakteryzują się własnością,
ze mały parametr występuje po lewej stronie. Aby się o tym przekonać wprowadzamy czas powolny ![]() Wtedy dostajemy układ
Wtedy dostajemy układ
Teraz równanie ruchu powolnego na ![]() (lokalnie
parametryzowanej przez
(lokalnie
parametryzowanej przez ![]() jest postaci
jest postaci
(z odpowiednią funkcją ![]()
Przeanalizujmy ruch typowego punktu ![]() Składa
się on z kawałków trzech rodzajów: dochodzenie do powierzchni
powolnej, ruch wzdłuż powierzchnii powolnej i ruch w obszarze przejściowym.
Składa
się on z kawałków trzech rodzajów: dochodzenie do powierzchni
powolnej, ruch wzdłuż powierzchnii powolnej i ruch w obszarze przejściowym.
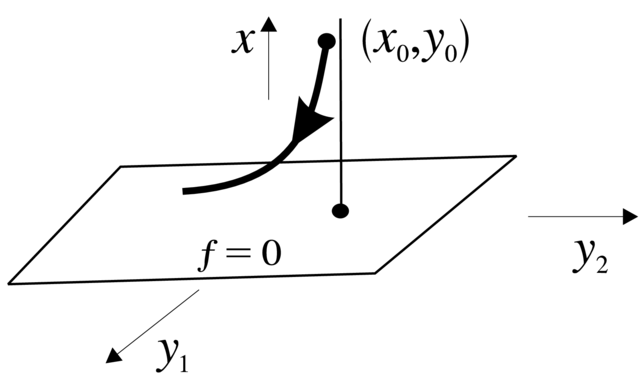
4.20. Dochodzenie do powierzchni powolnej. Niech punkt ![]() spoza
spoza ![]() rzutuje się (wzdłuż współrzędnych
rzutuje się (wzdłuż współrzędnych ![]() na punkt
na punkt ![]()
![]() , na
, na ![]() w obszarze stabilności (patrz Rysunek 4.6). To
znaczy, że punkt
w obszarze stabilności (patrz Rysunek 4.6). To
znaczy, że punkt ![]() leży w basenie przyciągania punktu
leży w basenie przyciągania punktu ![]() dla równania
dla równania ![]() (
(![]() stałe). Rozważmy obszar
stałe). Rozważmy obszar ![]() gdzie
gdzie ![]() jest pewnym obszarem odpowiadającum podzbiorowi obszaru stabilności w
jest pewnym obszarem odpowiadającum podzbiorowi obszaru stabilności w ![]() Okazuje się, że
powolny czas dochodzenia rozwiązania z warunkiem początkowym
Okazuje się, że
powolny czas dochodzenia rozwiązania z warunkiem początkowym ![]() do
do ![]() jest rzędu
jest rzędu ![]() co odpowiada rzeczywistemu
czasowi
co odpowiada rzeczywistemu
czasowi
(stała ![]() zależy od
zależy od ![]() i od
i od ![]()
4.21. Ruch powolny. W obszarze ![]() mamy ruch powolny, opisywany równaniem
mamy ruch powolny, opisywany równaniem ![]() Trwa on do momentu
Trwa on do momentu ![]() co odpowiada długiemu czasowi rzeczywistemu
co odpowiada długiemu czasowi rzeczywistemu ![]()
4.22. Ruch w obszarze przejściowym. Obszar przejściowy leży blisko granicy pomiędzy obszarami stabilności i niestabilności w ![]() Mamy dwie typowe możliwości (jak w teorii
bifurkacji):
Mamy dwie typowe możliwości (jak w teorii
bifurkacji):
A.![]() (gdzie
(gdzie ![]()
B.![]()
A. Zryw. Ten przypadek (który odpowiada bifurkacji siodło–węzeł) zanalizujemy dla sytuacji gdy ![]() i
i ![]() (można do tego wszystko zredukować). Po odpowiednich
przeskalowaniach mamy następujący układ
(można do tego wszystko zredukować). Po odpowiednich
przeskalowaniach mamy następujący układ
Dokonujemy normalizacji
łatwo sprawdzić, że prowadzi to do pola
orbitalnie równoważnemu polu ![]() Jego portret fazowy jest zadany równaniem
Riccatiego
Jego portret fazowy jest zadany równaniem
Riccatiego
| (4.12) |
i jest przedstawiony na Rysunku 4.717Równanie (4.12) jest chyba najprostszym przykładem równania różniczkowego, którego nie można rozwiązać w tzw. kwadraturach.. Zjawisko, które tutaj obserwujemy nosi nazwę zrywu.
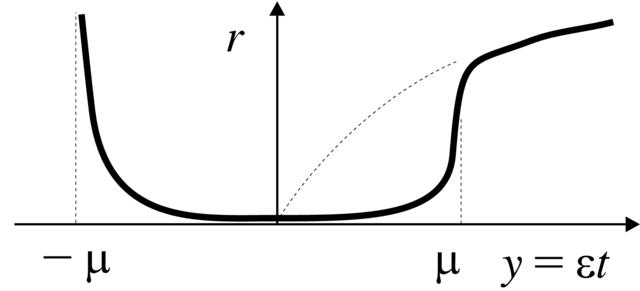
B. Opóźnienie utraty stabilności. W tym przypadku, który odpowiada bifurkacji Andronowa–Hopfa, problem redukuje się do następującego modelowego układu
| (4.13) |
![]()
![]() Oczywiście
Oczywiście ![]() jest `płynącym' parametrem. Załóżmy jeszcze, że
jest `płynącym' parametrem. Załóżmy jeszcze, że
przypadek ![]() jest mniej ciekawy. Dla amplitudy
jest mniej ciekawy. Dla amplitudy ![]() dostajemy równanie Bernoulliego
dostajemy równanie Bernoulliego
Połóżmy warunek początkowy
gdzie ![]() jest ustaloną (nie za dużą i nie za małą)
stałą. To zagadnienie początkowe ma następujące rozwiązanie
jest ustaloną (nie za dużą i nie za małą)
stałą. To zagadnienie początkowe ma następujące rozwiązanie
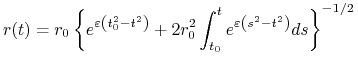 |
(4.14) |
(Zadanie 4.24). Zbadamy asymptotyczne zachowanie się tego rozwiązania przy ![]() dzieląc zakres czasu
dzieląc zakres czasu ![]() na
cztery obszary:
na
cztery obszary:
(a) ![]() czyli
czyli ![]()
Niech ![]() Wtedy
Wtedy ![]() i
i ![]() gdzie
gdzie ![]() Zatem
Zatem
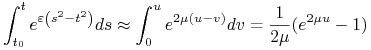 |
oraz
jest malejącą funkcją od ![]()
(b) ![]() jest ustalone tak, że
jest ustalone tak, że ![]()
Tutaj ![]() Zatem
Zatem
przy czym jest to bardzo szybkie dążenie do zera.
(c) ![]() czyli
czyli ![]() .
.
Wprowadźmy zmienną ![]() Jak w
punkcie (a) mamy
Jak w
punkcie (a) mamy ![]()
Obszar całkowania dla całki we wzorze (4.14) podzielimy na trzy odcinki:
od ![]() do
do ![]() , od
, od ![]() do
do ![]() i od
i od ![]() do
do ![]() Przez
Przez ![]()
![]() i
i ![]() oznaczymy odpowiednie całki. Podobnie jak w punkcie (a) pokazuje się, że
oznaczymy odpowiednie całki. Podobnie jak w punkcie (a) pokazuje się, że ![]() i
i ![]() Z rachunków w punkcie (b)
wynika, że
Z rachunków w punkcie (b)
wynika, że ![]() bardzo szybko. Zatem
bardzo szybko. Zatem
(d) ![]() czyli
czyli ![]() i jest ustalone. Teraz
i jest ustalone. Teraz
![]()
![]() Następnie
Następnie ![]() dla
dla ![]() bliskich
bliskich ![]() tj. dla tych
tj. dla tych ![]() dla których wkład do całki jest
dominujący. Dostajemy
dla których wkład do całki jest
dominujący. Dostajemy ![]() Stąd
Stąd
Możemy podsumować powyższe obliczenia.
Twierdzenie 4.23.W przypadku B opisywanego układem
(4.13) z ![]() zachodzi zjawisko opóźnienia utraty stabilności. Polega ono na tym, przy zmianie zmiennej
zachodzi zjawisko opóźnienia utraty stabilności. Polega ono na tym, przy zmianie zmiennej ![]() (która
jest współczynnikiem stabilności ruchu niezaburzonego) od wartości ujemnej
(która
jest współczynnikiem stabilności ruchu niezaburzonego) od wartości ujemnej ![]() do wartości dodatniej
do wartości dodatniej
![]() układ (względem
układ (względem ![]() jest cały czas
stabilny, a zmiana stabilności rozwiązania następuje dla
parametru
jest cały czas
stabilny, a zmiana stabilności rozwiązania następuje dla
parametru ![]() przy czym dalej amblituda oscylacji rośnie
jak w zwykłej bifurkacji Andronowa–Hopfa.
przy czym dalej amblituda oscylacji rośnie
jak w zwykłej bifurkacji Andronowa–Hopfa.
Zjawisko opóźnienia utraty stabilności można objaśnić fizycznie.Zmienna ![]() jest ujemna przez bardzo długi czas, rzędu
jest ujemna przez bardzo długi czas, rzędu ![]() Wtedy układ fizyczny zdąży
podejść bardzo blisko położenia równowagi; na tyle blisko,
że potrzeba potem tyle samo czasu, aby od położenia równowago
odejść (patrz Rysunek 4.8).
Wtedy układ fizyczny zdąży
podejść bardzo blisko położenia równowagi; na tyle blisko,
że potrzeba potem tyle samo czasu, aby od położenia równowago
odejść (patrz Rysunek 4.8).
ZADANIA
Zadanie 4.24. Udowodnić wzór (4.14).