2. Podstawowe metody prezentacji danych
2.1. Boxplot
Dla próby losowej ![]() zajmiemy się reprezentacją graficzną danych. Zaczniemy od boxplotu.
zajmiemy się reprezentacją graficzną danych. Zaczniemy od boxplotu.
-
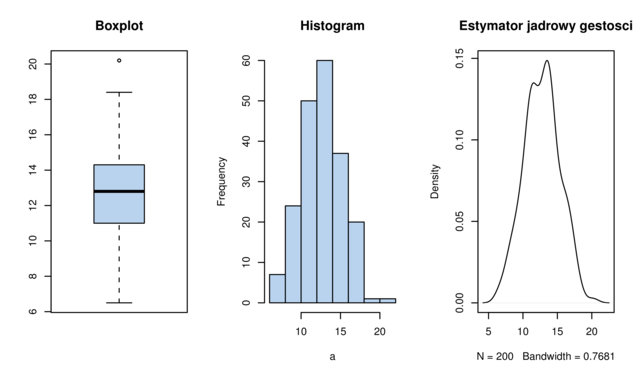
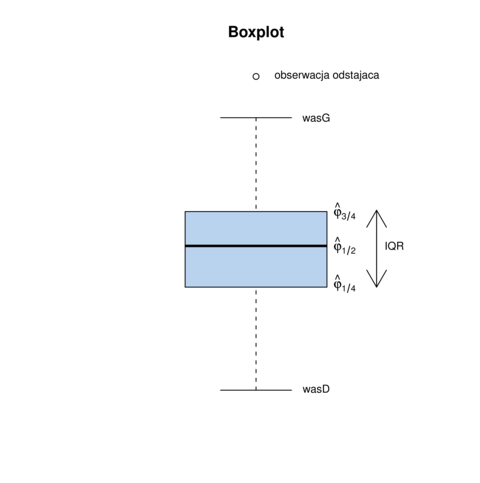
Boxplot. Przykładowy boxplot znajduje się na rysunku 2.1. Do jego narysowania potrzebne są następujące elementy:
-
kwartyle próbkowe
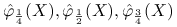 ;
; -
rozstęp międzykwartylowy (wysokość pudełka)
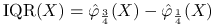 ;
; -
wąs górny
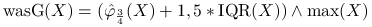 , gdzie
, gdzie 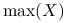 oznacza element maksymalny z próby;
oznacza element maksymalny z próby; -
wąs dolny
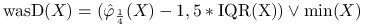 , gdzie
, gdzie 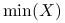 oznacza element minimalny z próby;
oznacza element minimalny z próby; -
obserwacje odstające, które nie mieszczą się w przedziale
![[\text{wasD}(X),\text{wasG}(X)]](wyklady/st2/mi/mi197.png) i nanosimy je oddzielnie w postaci punktów.
i nanosimy je oddzielnie w postaci punktów.
-
2.2. Estymacja gęstości
Załóżmy, że próba ![]() pochodzi z rozkładu o gęstości
pochodzi z rozkładu o gęstości ![]() i jest iid (niezależna o tym samym rozkładzie), będziemy szukać estymatora dla gęstości
i jest iid (niezależna o tym samym rozkładzie), będziemy szukać estymatora dla gęstości ![]() .
.
-
Histogram. Przykładowy histogram znajduje się na rysunku 2.1. Wybieramy dowolne
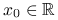 . Dla ustalonego
. Dla ustalonego 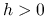 , oznaczającego szerokość klasy, tworzymy odcinki:
, oznaczającego szerokość klasy, tworzymy odcinki: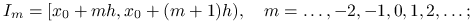
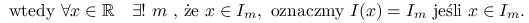
Histogramem nazywamy funkcję
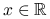 :
: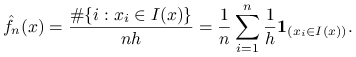
Uwaga 2.1
Podczas rysowania histogramu ważną kwestią jest dobór odpowiedniej szerokości przedziału, ![]() . Istnieje wiele konwencji wyboru, niektóre z nich to:
. Istnieje wiele konwencji wyboru, niektóre z nich to:
-
Jeżeli
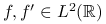 ,
, ![c=\left(\frac{6}{\int[f^{{\prime}}(x)]^{2}dx}\right)^{{\frac{1}{3}}}](wyklady/st2/mi/mi198.png) .
. -
Jeśli
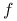 jest normalna,
jest normalna, 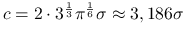 .
. -
Inny wybór to
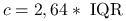 .
.
-
Estymator jądrowy gęstości. Przykładowy estymator jądrowy gęstości znajduje się na rysunku 2.1.
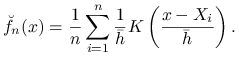
Dla budowy tego estymatora ważny jest dobór dwóch parametrów: szerokości pasma
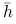 oraz funkcji jądra
oraz funkcji jądra 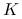 . Jądro jest gęstością dowolnego rozkładu, czyli jest dowolną funkcją określoną na
. Jądro jest gęstością dowolnego rozkładu, czyli jest dowolną funkcją określoną na 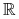 o własnościach
o własnościach 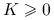 ,
, 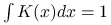 . Jednym z wyborów może być jądro postaci:
. Jednym z wyborów może być jądro postaci:![K_{e}(t)=\left\{\begin{array}[]{ll}\frac{3}{4\sqrt{5}}(1-\frac{1}{5}t^{2}),&\hbox{$|t|\leq\sqrt{5}$;}\\
0,&\hbox{wpp.}\end{array}\right.](wyklady/st2/mi/mi170.png)
Uwaga 2.2
-
Jeśli
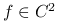 oraz
oraz 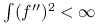 , to w klasie symetrycznych jąder
, to w klasie symetrycznych jąder 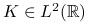 , asymptotycznie optymalne jest
, asymptotycznie optymalne jest 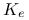 . Ponadto:
. Ponadto: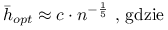
![c=\left[\int t^{2}K(t)dt\right]^{{-\frac{2}{5}}}\left[\int K^{2}(t)dt\right]^{{\frac{1}{5}}}\left[\int(f^{{\prime\prime}}(x))^{2}dx\right]^{{-\frac{1}{5}}}.](wyklady/st2/mi/mi182.png)
-
Jeśli
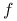 jest gęstością rozkładu normalnego, to
jest gęstością rozkładu normalnego, to 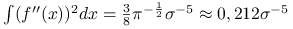 .
. -
Jeśli jądro
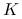 jest gęstością standardowego rozkładu normalnego oraz
jest gęstością standardowego rozkładu normalnego oraz 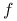 jest rozkładem normalnym, to
jest rozkładem normalnym, to 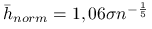 .
. -
Jeśli jądro jest równe
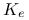 oraz
oraz 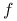 jest rozkładem normalnym, to
jest rozkładem normalnym, to 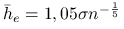
-
Domyślnie w programie R nastawiona jest metoda Silvermana wyboru parametru
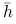 :
: 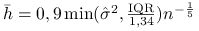 .
.
2.3. Przykłady w programie R
Estymator jądrowy gęstości:
-
dla danych Pima jednowymiarowy: http://www.mimuw.edu.pl/~pokar/StatystykaII/EKSPLORACJA/density.R
-
dla danych Pima dwuwymiarowy: http://www.mimuw.edu.pl/~pokar/StatystykaII/EKSPLORACJA/density2d.R
-
nastawianie szerokosci pasma w estymatorze jadrowym gestosci http://www.mimuw.edu.pl/~pokar/StatystykaII/EKSPLORACJA/bandwidth.pp.R