4. Skalowanie wielowymiarowe
Skalowanie wielowymiarowe pozwala na redukcję wymiaru cech. Dla macierzy danych:
![X=\left(\begin{array}[]{c}X_{1}^{T}\\
X_{2}^{T}\\
\ldots\\
X_{n}^{T}\\
\end{array}\right)_{{n\times p}}](wyklady/st2/mi/mi403.png) |
będziemy chcieli zrzutować ,,optymalnie” dane na ![]() , czyli zmniejszyć macierz
, czyli zmniejszyć macierz ![]() do
do ![]() o wymiarch
o wymiarch ![]() ,
, ![]() .
.
Optymalność zdefiniujemy w kategoriach macierzy odległości lub podobieństwa dla ![]() obiektów. Zadaniem będzie znalezienie optymalnej reprezentacji obiektów w
obiektów. Zadaniem będzie znalezienie optymalnej reprezentacji obiektów w ![]() .
.
Definicja 4.1
Macierz odległości to taka macierz, która spełnia własności:
Macierz podobieństwa jest macierzą konstruowaną w sposób przeciwstawny do macierzy odległości o własnościach:
4.1. Metody skalowania danych
Dla macierzy danych ![]() o wymiarach
o wymiarach ![]() , zdefiniujmy
, zdefiniujmy ![]() jako macierz odległości euklidesowych pomiędzy obiektami:
jako macierz odległości euklidesowych pomiędzy obiektami:
-
Classical multidimensional scaling:
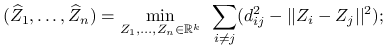
-
Sammon scaling:
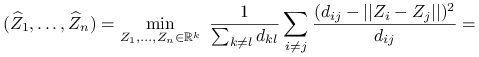
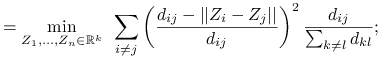
-
Kruskal-Shepard scaling:
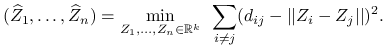
4.2. Własności
Niech ![]() oznacza macierz ortogonalną
oznacza macierz ortogonalną ![]() ,
, ![]() ,
, ![]() o wymiarze
o wymiarze ![]() . Oznaczmy
. Oznaczmy ![]() , czyli rzut
, czyli rzut ![]() na
na ![]() . Zdefiniujmy macierz odległości dla
. Zdefiniujmy macierz odległości dla ![]() jako
jako ![]() . Zauważmy, że:
. Zauważmy, że:
ponieważ mnożenie wektora przez macierz ortogonalną nie zmienia jego normy. Mamy więc:
![d_{{rs}}^{2}=\sum _{{j=1}}^{p}(X_{{rj}}-X_{{sj}})^{2}=\sum _{{j=1}}^{p}[l_{j}^{T}(X_{{r}}-X_{{s}})]^{2}\geq\sum _{{j=1}}^{k}[l_{j}^{T}(X_{{r}}-X_{{s}})]^{2}=\widehat{d}_{{rs}}^{2}.](wyklady/st2/mi/mi416.png) |
Stwierdzenie 4.1
Rzut ![]() na
na ![]() pierwszych składowych głównych minimalizuje wyrażenie
pierwszych składowych głównych minimalizuje wyrażenie ![]() wśród wszystkich rzutów
wśród wszystkich rzutów ![]() . Jest więc rozwiązaniem zadania classical multidimensional scaling.
. Jest więc rozwiązaniem zadania classical multidimensional scaling.
Przyjrzyjmy się następującej macierzy:
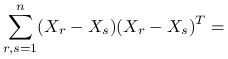 |
dla ![]() ,
,
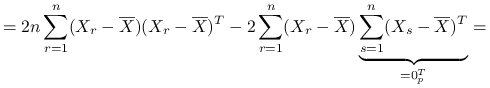 |
![=2n\text{ }\left(\begin{array}[]{ccc}\sum _{{r=1}}^{n}(X_{{r1}}-\overline{X}_{{.1}})^{2}&\ldots&\sum _{{r=1}}^{n}(X_{{r1}}-\overline{X}_{{.1}})(X_{{rp}}-\overline{X}_{{.p}})\\
\ldots&\ldots&\ldots\\
\sum _{{r=1}}^{n}(X_{{rp}}-\overline{X}_{{.p}})(X_{{r1}}-\overline{X}_{{.1}})&\ldots&\sum _{{r=1}}^{n}(X_{{rp}}-\overline{X}_{{.p}})^{2}\\
\end{array}\right)+0=](wyklady/st2/mi/mi418.png) |
gdzie ![]() jest macierzą kowariancji próbkowej (estymator obciążony).
jest macierzą kowariancji próbkowej (estymator obciążony).
Wróćmy do minimalizacji wyrażenia:
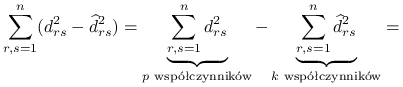 |
![=\underbrace{\sum _{{r,s=1}}^{n}\sum _{{j=k+1}}^{p}[l_{j}^{T}(X_{r}-X_{s})]^{2}}_{{\text{zostaje }p-k\text{ współczynników}}}.](wyklady/st2/mi/mi386.png) |
Ponieważ ![]() jest stałą, zadanie minimalizacji wyrażenia
jest stałą, zadanie minimalizacji wyrażenia ![]() jest równoważne zadaniu maksymalizacji
jest równoważne zadaniu maksymalizacji ![]() . Maksymalizujemy po ortogonalnym układzie wektorów
. Maksymalizujemy po ortogonalnym układzie wektorów ![]() wyrażenie:
wyrażenie:
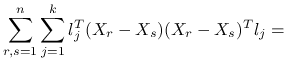 |
![=\sum _{{j=1}}^{k}l_{j}^{T}\left[\sum _{{r,s=1}}^{n}(X_{r}-X_{s})(X_{r}-X_{s})^{T}\right]l_{j}=](wyklady/st2/mi/mi411.png) |
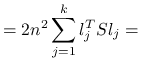 |
korzystając z rozkładu spektralnego ![]() ,
,
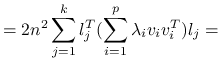 |
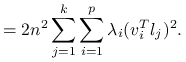 |
Dalszy dowód przebiega analogicznie do dowodu stwierdzenia 3.6. Można zauważyć związek pomiędzy własnościami składowych głównych dla podejścia populacyjnego i próbkowego.
∎4.3. Przykłady w programie R
Skalowanie wielowymiarowe:
-
porównanie skalowania wielowymiarowego i analizy składowych głównych dla danych Kraby: http://www.mimuw.edu.pl/~pokar/StatystykaII/EKSPLORACJA/mds.R
-
porównanie skalowania wielowymiarowego i analizy składowych głównych dla danych Iris i Kraby: http://www.mimuw.edu.pl/~pokar/StatystykaII/EKSPLORACJA/rzutDanych.R




