Zagadnienia

5.1 Test $\chi^{2}$ Pearsona
5.2 Test niezależności
5.3 Analiza odpowedniości (correspondence analysis)
5.4 Przykłady w programie R

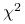5. Test $\chi^{2}$ i analiza odpowiedniości

Rozdział ten będzie dotyczył zmiennych jakościowych. Omawiane niżej testy $\chi^{2}$ i niezależności opierają się na odległości $\chi^{2}$ dla rozkładów dyskretnych (1.1). W obu przypadkach będziemy rozpatrywać odległości rozkładów zaobserwowanego od teoretycznego, dla których statystyka będzie asymptotycznie zbiegać do znanego rozkładu $\chi^{2}$ . Najpierw przyjrzyjmy się przypadkowi jednowymiarowemu.

5.1. Test 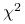$\chi^{2}$ Pearsona

Dana jest zmienna losowa jakościowa o rozkładzie wielomianowym o wartościach $\{ 1,\ldots,k\}$ oraz prawdopodobieństwach $(p_{1},\ldots,p_{k})$ . Podczas doświadczenia obserwujemy liczności, jakie przyjmowała zmienna w $n$ niezależnych próbach: $n=\widehat{n}_{1}+\widehat{n}_{2}+\ldots+\widehat{n}_{k}$ . Teoretyczne liczności będą wartościami oczekiwanymi dla rozkładu wielomianowego: $n_{1}=np_{1},\ldots,n_{k}=np_{k}$ . Satystyka wyraża się wzorem:

$Q=\sum _{{i=1}}^{k}\frac{(\widehat{n}_{i}-n_{i})^{2}}{n_{i}}\xrightarrow[n\rightarrow\infty]{d}\chi^{2}(k-1);$

przy spełnionej hipotezie zerowej $H_{0}:$ zmienna losowa pochodzi z rozkładu wielomianowego o parametrach $(p_{1},\ldots p_{k})$ , zbiega ona według rozkładu do rozkładu $\chi^{2}$ o $k-1$ stopniach swobody.

Omawianą statystykę można zapisać także jako:

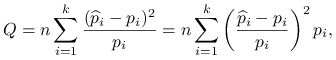$Q=n\sum _{{i=1}}^{k}\frac{(\widehat{p}_{i}-p_{i})^{2}}{p_{i}}=n\sum _{{i=1}}^{k}\left(\frac{\widehat{p}_{i}-p_{i}}{p_{i}}\right)^{2}p_{i},$

gdzie $\widehat{p}_{i}=\frac{\widehat{n}_{i}}{n}$ to zaobserwowane prawdopodobieństwa (będące stymatorami największej wiarygodności parametrów $p_{i}$ dla rozkładu wielomianowego).

5.2. Test niezależności

Będziemy rozpatrywać dwie zmienne losowe o rozkładzie dyskretnym:

$X\text{ o wartościach }\{ 1,\ldots,k\}$

$Y\text{ o wartościach }\{ 1,\ldots,l\},$

których rozkład łączny jest rozkładem wielomianowym o nieznanych parametrach $p_{{ij}}$ , $i=1,\ldots,k$ , $j=1,\ldots,l$ . Znane są jedynie zaobserwowane liczności dla każdej pary $(i,j)$ w postaci macierzy kontyngencji.

Definicja 5.1

Macierz kontyngencji to macierz $N$ o wymiarach $k\times l$ zawierająca zaobserwowane liczności $n_{{ij}}$ , $\sum _{{i=1}}^{k}\sum _{{j=1}}^{l}n_{{ij}}=n$ , dla każdej z par wartości zmiennych losowych $(X,Y)$ :

$\begin{array}[]{c|ccc}X\setminus Y&1&\ldots&l\\ \hline 1&n_{{11}}&\ldots&n_{{1l}}\\ \ldots&\ldots&\ldots&\ldots\\ k&n_{{k1}}&\ldots&n_{{kl}}\end{array}$

Hipotezę, którą będziemy testować to:

$H_{0}:\text{ zmienne losowe }X\text{ i }Y\text{ są niezależne.}$

W tym celu policzymy odległość rozkładu zaobserwowanego od teoretycznego rozumianego jako iloczyn rozkładów brzegowych. Macierz zaobserwowanych prawdopodobieństw możemy zapisać jako:

$(\widehat{p}_{{ij}})=\widehat{P}=\frac{N}{n},$

gdzie $N$ to macierz kontyngencji, a $n$ to suma wszystkich elementów tej macierzy. Statystyka testowa wyraża się wzorem:

$n\sum _{{i=1}}^{k}\sum _{{j=1}}^{l}\frac{(\widehat{p}_{{ij}}-\widehat{p}_{{i.}}\widehat{p}_{{.j}})^{2}}{\widehat{p}_{{i.}}\widehat{p}_{{.j}}}\xrightarrow[n\rightarrow\infty]{d}\chi^{2}\left((k-1)(l-1)\right),$

gdzie $\widehat{p}_{{i.}}=\sum _{{j=1}}^{l}\widehat{p}_{{ij}}$ i $\widehat{p}_{{.j}}=\sum _{{i=1}}^{k}\widehat{p}_{{ij}}$ to zaobserwowane rozkłady brzegowe dla $X$ i $Y$ .

5.3. Analiza odpowedniości (correspondence analysis)

Tak jak w poprzednim podrozdziale, dane mamy dwie zmienne losowe $X$ i $Y$ o rozkładzie dyskretnym. Analiza odpowiedniości to metoda prezentacji danych w przestrzeni o niewielkim wymiarze (zwykle równym 2, wtedy prezentację można przedstawić na płaszczyźnie), ilustrująca zależności pomiędzy danymi cechami $X$ i $Y$ .

Przykład 5.1

Rozpatrzmy następujący przykład: dla każdej osoby obserwujemy kolor oczu i włosów. Zmienna losowa $X$ będzie oznaczać jeden z czterech kolorów oczu: brown, blue, hazel, green. Zmienna losowa $Y$ będzie oznaczać jeden z czterech kolorów włosów: black, brown, red, blond. Tablica kontyngencji dla tego przykładu:

$\begin{array}[]{c|cccc}\text{eyes}\setminus\text{hair}&\text{black}&\text{brown}&\text{red}&\text{blond}\\ \hline\text{brown}&68&119&26&7\\ \text{blue}&20&84&17&94\\ \text{hazel}&15&54&14&10\\ \text{green}&5&29&14&16\end{array}$

Analiza odpowiedniości pozwoli nam na przedstawienie graficzne zależności pomiędzy kolorami włosów i oczu. Na przykład, będziemy mogli zobaczyć, czy osoby o niebieskim kolorze oczu mają najczęsciej włosy koloru blond.

Do analizy korespondencji potrzebna nam będzie macierz rezyduów Pearsona, której konstrukcję omówimy przy pomocy komend programu $R$ :

  N=table(cbind(X,Y)) # macierz kontyngencji, gdzie X i Y to faktory
  P=N/sum(N) # macierz zaobserwowanych prawdopodobieństw
  Pi=apply(P,1,sum) # rozkład brzegowy dla X
  Pj=apply(P,2,sum) # rozkład brzegowy dla Y
  PP=Pi%*%t(Pj)
  RP=sqrt(sum(N))*(P-PP)/sqrt(PP) # macierz rezyduów Pearsona

Uwaga 5.1

Zauważmy, że sum(RP^2) to statystyka testowa dla testu niezależności.

Przykład 5.1 Sama postać macierzy $RP$ może nam wiele powiedzieć o zależności poszczególnych cech. Macierz rezyduów Pearsona dla przykładu kolory oczu i włosów znajduje się w tabeli 5.1.

	BLACK	BROWN	RED	BLOND
Brown	4.40	1.23	-0.07	-5.85
Blue	-3.07	-1.95	-1.73	7.05
Hazel	-0.48	1.35	0.85	-2.23
Green	-1.95	-0.35	2.28	0.61

Tabela 5.1. Macierz rezyduów Pearsona dla przykładu kolory oczu i włosów.

Największe dodatnie wartości, a więc największą dodatnią zależność pomiędzy cechami mamy dla par (brown,black) i (blue,blond). Największą ujemne wartości, a więc największą ujemną zależność obserwujemy dla par (blue,black) i (brown,blond).

Celem analizy odpowiedniości jest przedstawienie cech $X$ i $Y$ na płaszczyźnie, żeby widoczne były zależności między nimi. W tym celu zmniejszymy wymiar $RP$ do 2, używając do tego analizy składowych głównych. Wiemy, że takie przybliżenie jest najlepsze w sensie błędu średniokwadratowego i opisuje możliwie najwięcej zmienności danych.

$RP=d_{1}u_{1}v_{1}^{T}+d_{2}u_{2}v_{2}^{T}+\ldots+d_{l}u_{l}v_{l}^{T}\approx$

$\approx(\sqrt{d_{1}}u_{1})(\sqrt{d_{1}}v_{1})^{T}+(\sqrt{d_{2}}u_{2})(\sqrt{d_{2}}v_{2})^{T}.$

Cechy $X$ i $Y$ przedstawiamy jako punkty:

$\widetilde{X}=[\sqrt{d_{1}}u_{1},\sqrt{d_{2}}u_{2}]$

$\widetilde{Y}=[\sqrt{d_{1}}v_{1},\sqrt{d_{2}}v_{2}].$

Pamiętamy z rozkładu SVD, że $(RP)V=UD$ , $U^{T}(RP)=DV^{T}$ , $U$ rozpina przestrzeń kolumn macierzy $RP$ , a $V$ przestrzeń wierszy. Scentrowane punkty (od kolumn macierzy $\widetilde{X}$ i $\widetilde{Y}$ odejmujemy średnie w kolumnach tak żeby środek danych był w (0,0)) nanosimy na wykres (rysunek 5.1).

$\par$

Rys. 5.1. Analiza odpowiedniości dla przykładu kolory oczu i włosów.

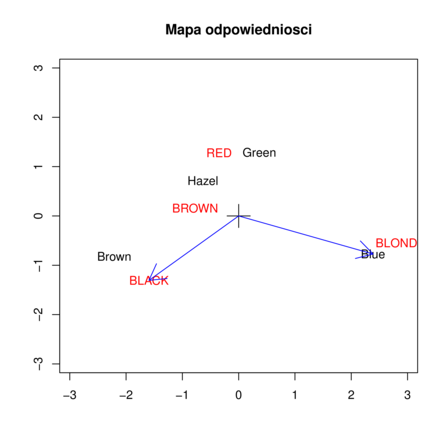
Przykład 5.1 Dla interpretacji mapy odpowiedniości, potraktujmy wiersze macierzy $\widetilde{X}$ oraz $\widetilde{Y}$ jako współrzędne wektorów, zaczepionych w punkcie (0,0). Wiersze macierzy $\widetilde{X}$ odpowiadają kolorom oczu, wiersze macierzy $\widetilde{Y}$ kolorom włosów. Na rysunku zaznaczone zostały dla przykładu wektory odpowiadające cechom blue oraz black. Zauważmy, że iloczyn skalarny dwóch wektorów, i-tego z macierzy $\widetilde{X}$ i j-tego z macierzy $\widetilde{Y}$ równy jest przybliżeniu macierzy rezyduów Pearsona. Oznaczmy:

$a=\widetilde{X}[i,]=(\sqrt{d_{1}}u_{1}[i],\sqrt{d_{2}}u_{2}[i]);$

$b=\widetilde{Y}[i,]=(\sqrt{d_{1}}v_{1}[i],\sqrt{d_{2}}v_{2}[i]);$

$RP\approx a^{T}b=a\circ b=|a||b|\cos(\vartheta),$

gdzie $\theta$ oznacza kąt pomiędzy wektorami. Interpretacja dla wektorów blue i black może być następująca: ponieważ długości obu wektorów są duże oraz $\cos(\vartheta)$ jest ujemne o wartości bezwzględnej w przybliżeniu $\frac{1}{2}$ , zależność pomiędzy cechami jest silnie ujemna. Na tej samej zasadzie możemy zaobserwować silną zależność pomiędzy włosami blond i oczami blue oraz włosami black i oczami brown.