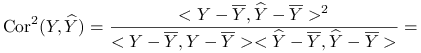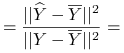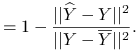9. Własności estymatorów MNK
9.1. Warunkowa wartość oczekiwana jako rzut ortogonalny
Definicja 9.1
Przypomnienie
Warunkowa wartość oczekiwana:
Niech ![]() będzie całkowalną zmienną losową w przestrzeni probabilistycznej
będzie całkowalną zmienną losową w przestrzeni probabilistycznej ![]() ,
, ![]()
![]() -ciałem takim, że
-ciałem takim, że ![]() . Warunkową wartością oczekiwaną
. Warunkową wartością oczekiwaną ![]() pod warunkiem
pod warunkiem ![]() nazywamy zmienną losową
nazywamy zmienną losową ![]() , że:
, że:
-
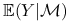 jest
jest 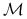 -mierzalna,
-mierzalna, -
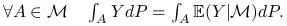
Załóżmy, że dla przestrzeni probabilistycznej ![]() określone zostały zmienne losowe całkowalne z kwadratem:
określone zostały zmienne losowe całkowalne z kwadratem: ![]()
![]()
![]() .
Zdefiniujmy
.
Zdefiniujmy ![]() (
(![]() ).
).
Stwierdzenie 9.1
![]() jest rzutem ortogonalnym
jest rzutem ortogonalnym ![]() na
na ![]() , gdzie
, gdzie ![]() jest
jest ![]() -ciałem generowanym przez
-ciałem generowanym przez ![]() , a
, a ![]() to miara prawdopodobieństwa warunkowego pod warunkiem zmiennej losowej
to miara prawdopodobieństwa warunkowego pod warunkiem zmiennej losowej ![]() .
.
Załóżmy, że ![]() jest rzutem ortogonalnym
jest rzutem ortogonalnym ![]() na
na ![]() . Wtedy
. Wtedy ![]()
![]()
![]()
![]() :
:
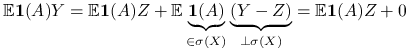 |
Z definicji warunkowej wartości oczekiwanej ![]() p.n.
p.n.
9.2. Twierdzenie Pitagorasa
Niech ![]() oznaczają zmienne losowe,
oznaczają zmienne losowe, ![]()
![]()
![]() ,
, ![]()
![]()
![]() . Zdefiniujmy iloczyn skalarny jako
. Zdefiniujmy iloczyn skalarny jako ![]() .
.
Twierdzenie 9.1
Pitagorasa
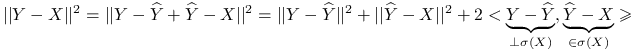 |
Wniosek 9.1
Rzut ortogonalny jest więc najlepszym przybliżeniem ![]() w klasie
w klasie ![]()
![]()
![]() w sensie:
w sensie:
Stwierdzenie 9.2
Jeśli ![]()
![]()
![]() , to
, to![]() .
.
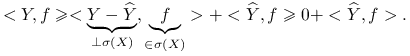 |
Stwierdzenie 9.3
Niech ![]() oznacza rzut
oznacza rzut ![]() na
na ![]() .
. ![]() jest rzutem
jest rzutem ![]() na przestrzeń
na przestrzeń ![]() . Rzut rzutu jest rzutem.
. Rzut rzutu jest rzutem.
Stwierdzenie 9.4
Oznaczmy ![]() jako rzut ortogonalny
jako rzut ortogonalny ![]() na lin
na lin![]() ,
, ![]() rzut
rzut ![]() na
na ![]() . Wtedy:
. Wtedy:
Ponieważ ![]()
![]()
![]() , równość wynika łatwo ze stwierdzenia 9.2.
, równość wynika łatwo ze stwierdzenia 9.2.
Definicja 9.2
Przypomnienie
Korelacja:
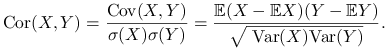 |
Współczynnik dopasowania ![]() to część zmienności
to część zmienności ![]() wyjaśnionej przez zmienność
wyjaśnionej przez zmienność ![]() :
:
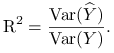 |
Błąd średniokwadratowy między ![]() i
i ![]() :
:
Twierdzenie 9.2
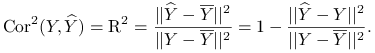 |
Twierdzenie 9.3
Pitagrorasa dla korelacji
Wniosek 9.2
Największą korelację ze wszystkich ![]() ,
, ![]() ma ze swoim rzutem ortogonalnym na przestrzeń rozpiętą przez
ma ze swoim rzutem ortogonalnym na przestrzeń rozpiętą przez ![]() :
:
Wniosek 9.3
Patrząc na wnioski 9.1 i 9.2 oraz twierdzenie 9.2 zauważmy, że zachodzi zależność:
Minimalizacja błędu średniokwadratowego ![]() Maksymalizacja kwadratu korelacji. Dla równoważnych problemów optymalnym jest rzut ortogonalny.
Maksymalizacja kwadratu korelacji. Dla równoważnych problemów optymalnym jest rzut ortogonalny.
Obrazuje tą zależność także kolejne stwierdzenie:
Stwierdzenie 9.5
Niech ![]() będą wystandaryzowanymi zmiennymi losowymi (
będą wystandaryzowanymi zmiennymi losowymi (![]() ,
, ![]() ,
, ![]() ,
, ![]() ). Wtedy:
). Wtedy:
Z twierdzenia 9.1 wynika jeszcze bardzo ważna zależność znana z rachunku prawdopodobieństwa:
Wniosek 9.4
gdzie ![]() .
.
W twierdzeniu 9.1 za ![]() podstawmy
podstawmy ![]() .
.