3. Obserwowalność
Rozpatrujemy następujący układ liniowy:
| (3.1) |
gdzie ![]() ,
, ![]() ,
, ![]() jest macierzą
jest macierzą ![]() oraz
oraz ![]() jest
macierzą
jest
macierzą ![]() .
.
Problem 3.1
Zagadnienie obserwowalności (Observability question):
dla zadanego
![]() odtworzyć
odtworzyć ![]() , a w szczególności
, a w szczególności ![]() .
.
Sens tego zagadnienia widać dla ![]() :
: ![]() to pomiary (obserwacje), z których należy odtworzyć
wielowymiarowe
to pomiary (obserwacje), z których należy odtworzyć
wielowymiarowe ![]() .
.
Definicja 3.1
Układ (3.1) nazywa się obserwowalny (observable), jeżeli dla
rozwiązań ![]() ,
, ![]() , z faktu, że
, z faktu, że ![]() , dla
, dla ![]() , wynika, że
, wynika, że
![]() .
.
Przykład 3.1
Jeżeli ![]() , to układ nie jest obserwowalny. Jeżeli
, to układ nie jest obserwowalny. Jeżeli ![]() i
i ![]() jest nieosobliwa, to
jest nieosobliwa, to
![]() i układ jest obserwowalny.
i układ jest obserwowalny.
Twierdzenie 3.1
Dwa następujące warunki są równoważne
-
(a) układ (3.1) jest obserwowalny;
-
(b)
![\mathrm{rank}\,\Big[C^{T},A^{T}C^{T},\ldots,\big(A^{T}\big)^{{n-1}}C^{T}\Big]=n](wyklady/tst/mi/mi463.png) , czyli
układ
, czyli
układ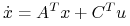
(3.2) jest lokalnie sterowalny.
Dowód: [19], str. 25, [27], str. 117.
![]()
1. Dowód ![]()
![]()
![]() , czyli
, czyli ![]()
![]()
![]() . Załóżmy więc
. Załóżmy więc ![]() , czyli, że układ (3.1) nie jest obserwowalny.
Istnieją wówczas punkty
, czyli, że układ (3.1) nie jest obserwowalny.
Istnieją wówczas punkty
![]() , t.ż.
, t.ż. ![]() ,
,
| (3.3) |
oraz ![]() dla każdego
dla każdego ![]() . Niech
. Niech
| (3.4) |
Stąd
| (3.5) |
czyli ![]() . Mamy
. Mamy ![]() dla
dla ![]() . Zatem
. Zatem
| (3.6) |
Zatem dla ![]() otrzymujemy
otrzymujemy ![]() , następnie różniczkując względem
, następnie różniczkując względem ![]() i wstawiając
i wstawiając
![]() otrzymujemy, że
otrzymujemy, że
| (3.7) |
Stąd ![]() , a więc
, a więc ![]() ,
czyli
,
czyli
| (3.8) |
Ponieważ ![]() , więc
, więc
![]() ,
co kończy dowód
,
co kończy dowód ![]()
![]()
![]() .
.
2. Dowód ![]()
![]()
![]() , czyli
, czyli ![]()
![]()
![]() . Załóżmy więc
. Załóżmy więc ![]() , czyli, że
, czyli, że
Zatem istnieje ![]() , t.ż.
, t.ż.
czyli ![]() dla każdego
dla każdego ![]() .
.
Z twierdzenia Cayleya–Hamiltona wynika, że
dla odpowiednich stałych ![]() (z wielomianu charakterystycznego).
(z wielomianu charakterystycznego).
Stąd ![]() . Następnie
. Następnie
a więc ![]() . Kontynuując otrzymujemy
. Kontynuując otrzymujemy ![]() dla każdego
dla każdego ![]() .
Mamy
.
Mamy
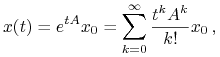 |
skąd otrzymujemy ![]() , a zatem układ (3.1) nie jest obserwowalny. To kończy dowód.
, a zatem układ (3.1) nie jest obserwowalny. To kończy dowód.




