6. Zagadnienie optymalnego sterowania
Badanie sterowalności jest jednym z podstawowych aspektów teorii sterowania. Kolejnym jest badanie optymalności pomyślnych sterowań. Wprowadzamy funkcjonał kosztu (cost functional) (lub funkcjonał wypłaty (payoff functional))
![{\mathfrak{C}}[u]=\int\limits _{0}^{{{t_{1}}}}{\mathfrak{f}}^{0}\Big(t,x(t),u(t)\Big)\mathrm{d}\, t+{\mathfrak{g}}({t_{1}},x({t_{1}}))\,,](wyklady/tst/mi/mi686.png) |
(6.1) |
gdzie ![]() jest odpowiedzią na sterowanie
jest odpowiedzią na sterowanie ![]() ,
, ![]() i
i ![]() są zadanymi
funkcjami rzeczywistymi. Pierwszy (całkowy) wyraz lewej strony (6.1) jest
bieżącym kosztem (running cost)
(lub bieżącą wypłatą (running payoff)), a drugi wyraz (tzn.
są zadanymi
funkcjami rzeczywistymi. Pierwszy (całkowy) wyraz lewej strony (6.1) jest
bieżącym kosztem (running cost)
(lub bieżącą wypłatą (running payoff)), a drugi wyraz (tzn. ![]() ) jest końcowym
kosztem (terminal cost) (lub końcową wypłatą (terminal payoff)). W przypadku
interpretacji
) jest końcowym
kosztem (terminal cost) (lub końcową wypłatą (terminal payoff)). W przypadku
interpretacji ![]() jako kosztu naturalne jest poszukiwanie sterowań
jako kosztu naturalne jest poszukiwanie sterowań ![]() minimalizujących
minimalizujących
![]() , a w przypadku interpretacji jako wypłaty — maksymalizujących. Dalej będziemy
mówili o koszcie i minimalizacji.
, a w przypadku interpretacji jako wypłaty — maksymalizujących. Dalej będziemy
mówili o koszcie i minimalizacji.
Rozpatrujemy więc zagadnienie:
z danymi początkowymi ![]() oraz funkcjonałem kosztu zadanym jednym z poniższych
wzorów
oraz funkcjonałem kosztu zadanym jednym z poniższych
wzorów
-
(L)
![\quad{\mathfrak{C}}[u]=\int\limits _{{0}}^{{{{t_{1}}}}}\mathfrak{f}^{0}(t,x(t),u(t))\,\mathrm{d}t\,,\qquad\qquad](wyklady/tst/mi/mi696.png) — zagadnienie Lagrange'a;
— zagadnienie Lagrange'a; -
(M)
![\quad{\mathfrak{C}}[u]=\mathfrak{g}({t_{1}},x({t_{1}}))\,,\qquad\qquad\qquad\;\;](wyklady/tst/mi/mi683.png) — zagadnienie Mayera;
— zagadnienie Mayera; -
(B)
![\quad{\mathfrak{C}}[u]=\int\limits _{{0}}^{{{{t_{1}}}}}\mathfrak{f}^{0}(t,x(t),u(t))\,\mathrm{d}t+\mathfrak{g}({t_{1}},x({t_{1}}))\,,\qquad](wyklady/tst/mi/mi691.png) — zagadnienie Bolzy.
— zagadnienie Bolzy.
Problem 6.1
Zagadnienie sterowania optymalnego (optimal control problem) polega
na tym, by doprowadzić do celu sterowaniem z odpowiedniej klasy, w taki sposób, by
![]() było możliwie najmniejsze.
było możliwie najmniejsze.
Definicja 6.1
Niech klasa pomyślnych sterowań (successful controls) będzie oznaczona przez
Sterowanie ![]() jest optymalne (optimal), jeżeli
jest optymalne (optimal), jeżeli
| (6.2) |
Dla zagadnienia Bolzy (B) (lub zagadnienia Lagrange'a (L)), zadanego sterowania ![]() i odpowiedzi
i odpowiedzi ![]() określamy
określamy
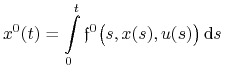 |
Jeżeli ![]() jest pomyślne, to
jest pomyślne, to ![]() (dla pewnego
(dla pewnego ![]() )
i odpowiedni koszt to
)
i odpowiedni koszt to ![]() . Gdy
. Gdy ![]() jest optymalne, to
jest optymalne, to ![]() jest najmniejsze.
jest najmniejsze.
Określamy ![]() –wymiarowy wektor
–wymiarowy wektor ![]() oraz
oraz
W ten sposób zagadnienie Bolzy (B) (lub zagadnienie Lagrange'a (L)) można sprowadzić do zagadnienia Mayera (M) dla
| (6.3) |
z
| (6.4) |
Cel może być ustalony, lub nie:
-
(I) Gdy, tak jak w poprzednich rozdziałach, cel jest ustalony mamy do czynienia z zagadnieniem ustalonego punktu końcowego,
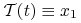 ,
, 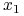 jest
ustalonym punktem w
jest
ustalonym punktem w 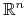 ,
,  jest wówczas czasem dotarcia do celu
jest wówczas czasem dotarcia do celu 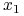 i nie jest ustalone (fixed–end–point (a target point is given)
– free–time problem);
i nie jest ustalone (fixed–end–point (a target point is given)
– free–time problem); -
(II) Można rozpatrywać zagadnienie, gdy cel
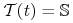 , gdzie
, gdzie 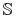 jest
jest 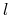 –wym. (
–wym. (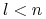 ) gładką rozmaitością (manifold; por. [12], str. 64)
w
) gładką rozmaitością (manifold; por. [12], str. 64)
w 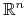 — podobnie jak powyżej
— podobnie jak powyżej 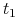 nie jest ustalone;
nie jest ustalone; -
(III) Cel może nie być określony i wtedy mamy do czynienia z zagadnieniem swobodnego punktu końcowego (free–end–point problem; a target point is not given): wtedy
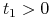 jest ustalone,
jest ustalone, 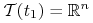 .
.
Definicja 6.2
Sterowanie ![]() jest czaso–optymalne (time–optimal)
(lub optymalno-czasowe), jeżeli jest optymalne dla funkcjonału kosztu
jest czaso–optymalne (time–optimal)
(lub optymalno-czasowe), jeżeli jest optymalne dla funkcjonału kosztu
| (6.5) |
gdzie ![]() jest chwilą przybycia do celu
jest chwilą przybycia do celu ![]() .
.




