1. Wstęp

Teoria sterowania (z Wikipedii):

,,Pożądaną wartość wyjścia układu nazywamy wartością zadaną. Kiedy od jednego lub więcej wyjść układu wymagamy specyficznego zachowania się w czasie, regulator próbuje manipulować wejściem układu tak, aby jego wyjście zachowywało się w pożądany sposób. Jako przykład posłuży nam sterowanie samochodem, przy czym zależy nam na utrzymaniu stałej jego prędkości. W tym przypadku układem jest samochód, wielkością wyjściową układu - prędkość, wielkością wejściową - przesunięcie pedału gazu, a wartością zadaną - pożądana prędkość.”

,,Control theory is an interdisciplinary branch of engineering and mathematics, that deals with the behavior of dynamical systems. The desired output of a system is called the reference. When one or more output variables of a system need to follow a certain reference over time, a controller manipulates the inputs to a system to obtain the desired effect on the output of the system.”

,,Field of applied mathematics that is relevant to the control of certain physical processes and systems. Although control theory has deep connections with classical areas of mathematics, such as the calculus of variations and the theory of differential equations, it did not become a field in its own right until the late 1950s and early 1960s. At that time, problems arising in engineering and economics were recognized as variants of problems in differential equations and in the calculus of variations, though they were not covered by existing theories. At first, special modifications of classical techniques and theories were devised to solve individual problems. It was then recognized that these seemingly diverse problems all had the same mathematical structure, and control theory emerged.”

Z książki [38]:

,,Mathematical control theory is the area of application–oriented mathematics that deals with the basic principles underlying the analysis and design of control systems. To control an object means to influence its behavior so as to achieve a desired goal. In order to implement this influence, engineers build devices that incorporate various mathematical techniques. These devices range from Watt's steam engine governor, designed during the English Industrial Revolution, to the sophisticated microprocessor controllers found in consumer items — such as CD players and automobiles — or in industrial robots and airplane autopilots.”

Francuski: Régulation

Włoski: Teoria del controllo

Niemiecki: Regelungstheorie (Kontrolltheorie)

Czeski: Teorie řizeni

Hiszpański: Teoria del control

Informacje ogólne:

Kod przedmiotu: 1000-135TST Kod SOCRATES: 11103 Nazwa przedmiotu: Teoria sterowania

Punkty ECTS i inne: 6.00

Rodzaj przedmiotu: fakultatywne Założenia: Analiza matematyczna II, równania różniczkowe zwyczajne

Krótki opis: Wykład jest wstępem do współczesnej teorii sterowania. Teoria jest ilustrowana licznymi przykładami z ekonomii, biologii, medycyny, fizyki i techniki.

Plan wykładu:

Zagadnienie sterowania
Zagadnienie sterowania optymalnego
Klasy sterowania
Przykłady z ekonomii, biologii, medycyny, fizyki i techniki
Twierdzenia o lokalnej i globalnej (całkowitej) sterowalności dla układów liniowych i nieliniowych
Zasada ,,bang–bang” dla układów liniowych
Liniowe zagadnienie sterowania optymalnego, szczególny przypadek Zasady Maksimum Pontragina, istnienie sterowania czaso–optymalnego
Zasada Maksimum Pontragina

Notatki te są głównie oparte na podręcznikach

Macki, Strauss [31],
Evans [19],
Pontryagin, Boltyansky, Gamkrelidze, Mishchenko [36],
Bressan, Piccoli [14]

oraz w mniejszym stopniu na

Knowles [27],
Hocking [24].

Ponadto gorąco zachęcam czytelnika do przejrzenia następującej literatury: [1, 2, 7, 8, 11, 13, 18, 20, 25, 26, 28, 29, 33, 38, 39, 40, 41].

Niektóre dowody nie są przytoczone, a czytelnik jest odesłany do odpowiedniej literatury. Nie oznacza to jednak, że są to dowody w jakimś sensie ,,mniej ważne”: stanowią one istotną część wykładu. Takie dowody będą oznaczane symbolem $\,\clubsuit\,$ . Koniec dowodu będzie oznaczany $\,\square\,$ .

Historia: por. [3]; [38], str. 22; [6], str. 4; [20], str. 2–3, 124–128.

Christiaan Huygens (1629–1695), holenderski matematyk i fizyk, zajmował się zegarami wahadłowymi i badał sterowanie prędkością,
James Clerk Maxwell (1831–1879), szkocki fizyk i matematyk, analiza dynamiki regulatora odśrodkowego obrotów (centrifugal governor),
Edward John Routh (1831–1907), matematyk angielski, uogólnienie wyników Maxwella na ogólny układ liniowy,
Adolf Hurwitz (1859–1919), matematyk niemiecki, badanie stabilności: twierdzenie Routha-Hurwitza,
Alexander Lyapunov (1857–1918), matematyk rosyjski, teoria stabilności (stability theory),
Harold S. Black (1898–1983), inżynier amerykański, wprowadził pojęcie ujemnego sprzężenia zwrotnego (negative feedback),
Harry Nyquist (1889–1976), amerykański elektrotechnik (automatyk) pochodzenia szwedzkiego, twórca kryterium stabilności dla układów ze sprzężeniem zwrotnym,
Richard Bellman (1920–1984), amerykański matematyk stosowany, rozwinął programowanie dynamiczne (dynamic programming),
Andrey Kolmogorov (1903–1987), matematyk rosyjski, współtwórca filtra Wienera-Kolmogorova,
Norbert Wiener (1894–1964), matematyk amerykański pochodzący z Polski, współtwórca filtra Wienera–Kolmogorova, twórca cybernetyki (cybernetics),
Lev Pontryagin (1908–1988), matematyk rosyjski, wprowadził zasadę maksimum i zasadę bang-bang.

Przykład 1.1 (Ekonomia narodowa (por. [31]))

Ekonomia typowego kraju kapitalistycznego jest b. skomplikowanym układem utworzonym z populacji (konsumenci, producenci, …), spółek, dóbr materialnych, produktów, dostępnych środków pieniężnych, kredytów, etc.

Stan układu określa zbiór danych: zarobków, zysków, strat, wyprzedaży dóbr i usług, inwestycji, bezrobocia, zasiłków społecznych, współczynników inflacji, wymiany zagranicznej środków pieniężnych.

Rząd może wpływać na stan układu stosując różnego typu sterowania (controls), n.p. politykę podatkową, kontrolowanie zarobków i cen.

Przykład 1.2 (Wagon odrzutowy (rocket car) — por. [27], str. 1, [31], str. 3, [19], str. 9, [14], str. 5–7)

Rozważamy ,,wagon odrzutowy” o masie $m=1$ poruszający się po linii prostej bez tarcia. Oznaczamy przez $x=x(t)$ położenie środka masy w chwili $t>0$ . Równanie ruchu (prawo Newtona) ma postać równania różniczkowego zwyczajnego:

${\ddot{x}}=u\,,\qquad t>0\,,$

(1.1)

gdzie ${\ddot{x}}$ oznacza drugą pochodną funkcji $x$ , oraz $u=u(t)$ jest zewnętrzną siłą działającą na wagon (sterowaniem (control)). Początkowe położenie i prędkość określone są przez $x(0)=x_{0}$ oraz ${\dot{x}}(0)=y_{0}$ . Celem jest dobranie $u$ w taki sposób, by wagon dotarł do wybranego punktu, n.p. $0$ , i osiągnął wtedy prędkość $0$ (zagadnienie sterowania (control problem)) w możliwie najkrótszym czasie (zagadnienie sterowania czaso–optymalne (time optimal control problem)). Naturalne jest założenie, że funkcja $u$ jest ograniczona, n.p.

$|u(t)|\leq 1\,.$

Zagadnienie ma charakter dwuwymiarowy:

$x^{1}:=x\,,\qquad x^{2}:={\dot{x}}\,.$

Mamy wiec układ RRZ $2\times 2$ :

${\dot{x}}^{1}=x^{2}\,,\qquad{\dot{x}}^{2}=u\,,\qquad u=u(t)\,,$

lub w postaci macierzowej:

$\left[\begin{array}[]{c}{\dot{x}}^{1}\\ {\dot{x}}^{2}\end{array}\right]\,=\,\left[\begin{array}[]{cc}0&1\\ 0&0\\ \end{array}\right]\left[\begin{array}[]{c}{x}^{1}\\ {x}^{2}\end{array}\right]+\left[\begin{array}[]{c}0\\ 1\end{array}\right]u(t)$

Zagadnienie sterowania sprowadza się do znalezienia takiej funkcji $u$ , żeby dla pewnego ${{t_{1}}}>0$ zachodziło

$\left[\begin{array}[]{c}{x}^{1}({{t_{1}}})\\ {x}^{2}({{t_{1}}})\end{array}\right]\,=\,\left[\begin{array}[]{c}0\\ \par \end{array}\right]\,,$

dla odpowiedniego rozwiązania, a zagadnienie sterowania czaso–optymalnego, by dodatkowo ${{t_{1}}}$ było możliwie najmniejsze.

Przykład 1.3 (Wymuszony oscylator harmoniczny (por. [27], str. 2, [19], str. 7))

Kontrolny element samolotu powinien być utrzymywany w ustalonym właściwym położeniu. zakładamy, że odbywa się to według wymuszonego oscylatora harmonicznego, tzn. dla $y$ — odchylenia od właściwego położenia, odpowiednie RRZ ma postać

${\ddot{y}}=-l{\dot{y}}-h_{0}y+u\,,$

gdzie wyraz $-l{\dot{y}}$ jest siłą oporu ośrodka, $-h_{0}y$ siłą sprężystości oraz $u$ — zewnętrzną siła (sterowaniem). Ponieważ wychylenia kontrolnego elementu w samolocie są niedopuszczalne, celem jest doprowadzenie układu do stanu $y=0$ , $\dot{y}=0$ w możliwie najkrótszym czasie. Zagadnienie ma postać macierzową

$\left[\begin{array}[]{c}{\dot{x}}^{1}\\ {\dot{x}}^{2}\end{array}\right]\,=\,\left[\begin{array}[]{cc}0&1\\ -h_{0}&-l\\ \end{array}\right]\left[\begin{array}[]{c}{x}^{1}\\ {x}^{2}\end{array}\right]+\left[\begin{array}[]{c}0\\ 1\end{array}\right]u(t)$

Przykład 1.4 (Zysk firmy (por. [27], str. 3))

$x(t)$ określa zysk pewnej firmy w czasie $t$ . Zysk może zostać przeznaczony na

dalszą produkcję
konsumpcję

$u=u(t)$ ( $0\leq u(t)\leq 1$ ) określa część zysku przeznaczoną na dalszą produkcję. Odpowiednie RRZ ma postać

${\dot{x}}=kux\,,$

gdzie $k$ jest danym współczynnikiem.

Zagadnienie polega na znalezieniu $u=u(t)$ takiego, by całkowita konsumpcja na pewnym odcinku czasu $[0,{{t_{1}}}]$ , czyli

${\mathfrak{C}}[u]=\int\limits _{0}^{{{{t_{1}}}}}\Big(1-u(t)\Big)\, x(t)\,{\rm d}t\,,$

była największa.

Przykład 1.5 (Wzrost rośliny (por. [24], str. 2))

Ogrodnik chce wyhodować roślinę o zadanej wysokości. Naturalny proces wzrostu może być przyspieszony przez sztuczne oświetlanie rośliny, prowadząc do zredukowania godzin bez światła, gdy roślina nie rośnie. Niech $x=x(t)$ będzie wysokością rośliny w chwili $t$ . RRZ opisujące wzrost rośliny ma postać

${\dot{x}}=1+u\,,$

(1.2)

gdzie $u=u(t)$ opisuje dodatkowy przyrost rośliny spowodowany przez sztuczne oświetlenie. Załóżmy, że początkowa wysokość rośliny wynosi $0$ , a pożądana wysokość po jednostce czasu $t=1$ powinna być dwie jednostki,

$x(0)=0\,,\qquad x(1)=2\,.$

(1.3)

,,Koszt” sztucznego oświetlenia określa funkcja

${\mathfrak{C}}[u]=\int\limits _{0}^{1}\frac{\big(u(t)\big)^{2}}{2}\,{\rm d}t\,.$

Zagadnienie polega na znalezieniu sterowania $u$ , takiego że odpowiednie rozwiązanie (1.2) spełnia (1.3) oraz ${\mathfrak{C}}$ przyjmuje najmniejszą wartość (zagadnienie sterowania optymalnego).

Rozwiązanie (1.2) spełniające (1.3) ma postać

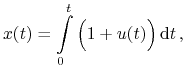$x(t)=\int\limits _{0}^{t}\Big(1+u(t)\Big)\,{\rm d}t\,,$

gdzie $u$ spełnia

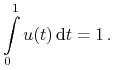$\int\limits _{0}^{1}u(t)\,{\rm d}t=1\,.$

(1.4)

Z (1.4) możemy przekształcić

${\mathfrak{C}}[u]=\int\limits _{0}^{1}\frac{(u(t)-1)^{2}}{2}\,{\rm d}t+\frac{1}{2}$

Stąd widać, że minimum, to ${\mathfrak{C}}[u]=\frac{1}{2}$ . Jest ono osiągane dla $u\equiv 1$ na $[0,1]$ . Optymalne rozwiązanie ma postać $x(t)=2t$ , $t\in[0,1]$ .

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.