7. Liniowe zagadnienie czaso–optymalne
Rozpatrujemy liniowe zagadnienie sterowania optymalnego (LA):
| (7.1) |
gdzie ![]() i
i ![]() są stałymi macierzami
są stałymi macierzami ![]() i
i ![]() , odpowiednio, a
funkcjonał kosztu jest określony przez (6.5).
, odpowiednio, a
funkcjonał kosztu jest określony przez (6.5).
Definicja 7.1
Niech ![]() będzie zbiorem osiągalnym (reachable set) z
będzie zbiorem osiągalnym (reachable set) z ![]() w
chwili
w
chwili ![]() :
:
| (7.2) |
![]() może być zanurzony w odpowiedniej hiperpłaszczyźnie (hyperplane)
w
może być zanurzony w odpowiedniej hiperpłaszczyźnie (hyperplane)
w ![]() . Wówczas
. Wówczas ![]() i
i ![]() będą rozumiane
w sensie odpowiednich hiperpłaszczyzn.
będą rozumiane
w sensie odpowiednich hiperpłaszczyzn.
Dla zwartych podzbiorów ![]() ,
, ![]() przestrzeni
przestrzeni ![]() rozważamy metrykę Hausdorffa
rozważamy metrykę Hausdorffa
![]() jest
jest ![]() –otoczką zbioru
–otoczką zbioru ![]() (
(![]() –sack about
–sack about ![]() )
)
Lemat 7.1
Dla (LA): Zbiór ![]() jest wypukły i zwarty
(convex and compact). Ponadto odwzorowanie
jest wypukły i zwarty
(convex and compact). Ponadto odwzorowanie ![]() ,
,
![]() , jest ciągłe z topologią w obrazie zdefiniowaną przez metrykę Hausdorffa.
, jest ciągłe z topologią w obrazie zdefiniowaną przez metrykę Hausdorffa.
Dowód: [19], str. 32, [31], str. 60.
![]() Mamy
Mamy
![y\in\mathbb{K}(t;x_{0})\quad\Leftrightarrow\quad\exists\, u\in\mathbb{U}_{m}[0,t]\,:\quad y=e^{{At}}x_{0}+\int\limits _{0}^{t}e^{{A(t-s)}}Bu(s)\,\mathrm{d}s\,.](wyklady/tst/mi/mi817.png) |
(7.4) |
-
Wypukłość.
![x_{i}\in\mathbb{K}(t;x_{0})\quad\Leftrightarrow\quad\exists\, u_{i}\in\mathbb{U}_{m}[0,t]\,:\quad x_{i}=e^{{At}}x_{0}+\int\limits _{0}^{t}e^{{A(t-s)}}Bu_{i}(s)\,\mathrm{d}s\,\quad i=1,2\,.](wyklady/tst/mi/mi730.png)
Wtedy dla
![\lambda\in[0,1]](wyklady/tst/mi/mi769.png)
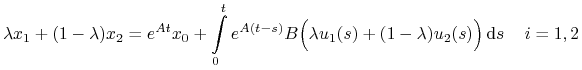
i
![\lambda u_{1}+(1-\lambda)u_{2}\in\mathbb{U}_{m}[0,t]\,.](wyklady/tst/mi/mi723.png)
Zatem
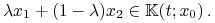
-
Zwartość. Pokażemy domkniętość. Niech
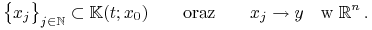
Chcemy pokazać, że
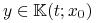 . Ponieważ
. Ponieważ 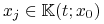 ,
to istnieje
,
to istnieje ![u_{j}\in\mathbb{U}_{m}[0,t]](wyklady/tst/mi/mi714.png) , t.ż.
, t.ż.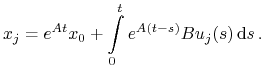
Z twierdzenia Alaoglu istnieje podciąg
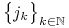 ,
,
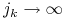 , dla
, dla 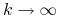 oraz istnieje
oraz istnieje ![u\in\mathbb{U}_{m}[0,t]](wyklady/tst/mi/mi931.png) ,
t. ż.
,
t. ż.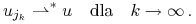
Stąd przechodząc do podciągu (por. rozdział 5)
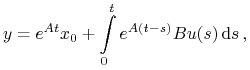
a zatem
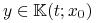 i
i 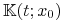 jest domknięty, ponadto jest
ograniczony, a więc zwarty.
jest domknięty, ponadto jest
ograniczony, a więc zwarty. -
Ciągłość. Dla
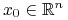 ,
, 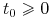 oraz
oraz 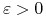 pokażemy, że istnieje
pokażemy, że istnieje
![\delta\in\,]\, 0,1\,[\,](wyklady/tst/mi/mi873.png) , t.ż. spełniony jest następujący warunek:
, t.ż. spełniony jest następujący warunek:-
jeżeli
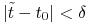 , to
, to 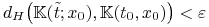 .
.
Chcemy więc pokazać, że jeżeli
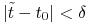 , to
, to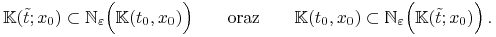
Niech
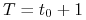 ,
, 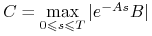 .
.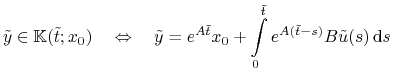
dla pewnego
![\tilde{u}\in\mathbb{U}_{m}[0,\tilde{t}]](wyklady/tst/mi/mi905.png) .
.Przedłużamy
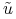 zerem na
zerem na ![[0,T]](wyklady/tst/mi/mi899.png) (czyli
(czyli 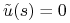 dla
dla ![t\in\,]\tilde{t},T]](wyklady/tst/mi/mi789.png) ) oraz
określamy
) oraz
określamy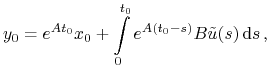
zatem
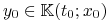 .
.Mamy
![\begin{array}[]{ll}&|\tilde{y}-y_{0}|=|e^{{A\tilde{t}}}x_{0}-e^{{At_{0}}}x_{0}|+\Big|\int\limits _{0}^{{\tilde{t}}}e^{{A(\tilde{t}-s)}}B\tilde{u}(s)\,\mathrm{d}s-\int\limits _{0}^{{{t}_{0}}}e^{{A({t}_{0}-s)}}B\tilde{u}(s)\,\mathrm{d}s\Big|\\
&\leq|e^{{A\tilde{t}}}-e^{{At_{0}}}||x_{0}|+|e^{{A\tilde{t}}}-e^{{At_{0}}}|\Big|\int\limits _{0}^{{\tilde{t}}}e^{{-As}}B\tilde{u}(s)\,\mathrm{d}s\Big|+|e^{{At_{0}}}|\Big|\int\limits _{{t_{0}}}^{{\tilde{t}}}e^{{-As}}B\tilde{u}(s)\,\mathrm{d}s\Big|\,.\end{array}](wyklady/tst/mi/mi718.png)
Niech
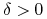 będzie t.ż. dla
będzie t.ż. dla 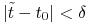 mamy
mamy 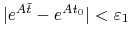 ,
gdzie
,
gdzie 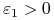 będzie wybrane później. Mamy
będzie wybrane później. Mamy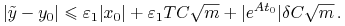
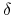 i
i 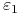 wybieramy takie, aby
wybieramy takie, aby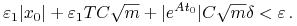
Stąd wynika, że
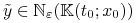 , a z dowolności
, a z dowolności 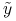 , że
, że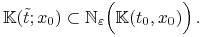
Identycznie pokazujemy, że
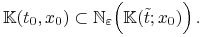
-
Warto zauważyć, że podobny wynik nie jest prawdziwy dla (NLA) — por. [14], str. 52.
Można teraz sformułować twierdzenie o istnieniu sterowania czaso–optymalnego
Twierdzenie 7.1
Dla (LA): jeżeli istnieje pomyślne sterowanie prowadzące ![]() do celu
do celu ![]() , to istnieje sterowanie czaso–optymalne i jest ono bang-bang.
, to istnieje sterowanie czaso–optymalne i jest ono bang-bang.
Dowód: [19], str. 31; [31], str. 60; [36], str. 147; por. [27], str. 173.
![]()
Istnieje pomyślne sterowanie, a zatem ![]() dla pewnego
dla pewnego ![]() .
Niech
.
Niech
| (7.5) |
Zbiór ![]() jest więc niepusty i ograniczony z dołu.
Istnieje więc
jest więc niepusty i ograniczony z dołu.
Istnieje więc ![]() . Chcemy pokazać, że
. Chcemy pokazać, że
co oznacza, że istnieje sterowanie prowadzące do celu w najkrótszym czasie ![]() .
.
Załóżmy, że ![]() . Ponieważ
. Ponieważ ![]() jest domknięty, to
istnieje otwarta kula
jest domknięty, to
istnieje otwarta kula ![]() ,
, ![]() , t.ż.
, t.ż.
Korzystając z ciągłości przekształcenia ![]() otrzymujemy
otrzymujemy
dla pewnego ![]() .
.
To oznacza, że ![]() nie jest osiągalny dla pewnych
nie jest osiągalny dla pewnych ![]() , co jest sprzeczne z
definicją
, co jest sprzeczne z
definicją ![]() .
.
Z zasady bang–bang: jeżeli istnieje pomyślne sterowanie z ![]() prowadzące
prowadzące ![]() do
do ![]() w czasie
w czasie ![]() , to istnieje sterowanie bang–bang prowadzące
, to istnieje sterowanie bang–bang prowadzące ![]() do
do ![]() w czasie
w czasie ![]() . To kończy dowód.
. To kończy dowód.
Definicja 7.2
Sterowanie ![]() określone na
określone na ![]() jest ekstremalne (extremal),
jeżeli
jest ekstremalne (extremal),
jeżeli
| (7.6) |
gdzie ![]() oznacza brzeg zbioru.
oznacza brzeg zbioru.
Należy zauważyć, że sterowanie ekstremalne nie musi być ani optymalne, ani nawet pomyślne!
W momencie dotarcia do celu, odpowiedż na sterowanie czaso–optymalne leży na brzegu zbioru
![]() :
:
Lemat 7.2
Jeżeli sterowanie ![]() jest czaso–optymalne, to w
jest czaso–optymalne, to w ![]() — momencie dotarcia do celu
— momencie dotarcia do celu
![]() — odpowiedź
— odpowiedź ![]() leży w
leży w
![]() (czyli
(czyli ![]() ).
).
Dowód
Załóżmy, że ![]() jest czaso–optymalnym sterowaniem prowadzącym
jest czaso–optymalnym sterowaniem prowadzącym ![]() do
do
![]() w czasie
w czasie ![]() , czyli
, czyli
i ![]() nie leży w
nie leży w ![]() .
.
Wówczas istnieje (otwarta) kula ![]() . Z ciągłości
przekształcenia
. Z ciągłości
przekształcenia ![]() istnieje
istnieje ![]() , t.ż.
, t.ż.
zatem cel ![]() byłby osiągalny w czasie
byłby osiągalny w czasie ![]() , co jest sprzeczne z
minimalnością
, co jest sprzeczne z
minimalnością ![]() .
.
Odpowiedź na dowolne sterowanie nie może przechodzić z wnętrza zbioru osiągalnego na jego brzeg:
Lemat 7.3
Załóżmy, że dla sterowania ![]()
gdzie ![]() jest odpowiedzią
jest odpowiedzią ![]() .
.
Wówczas
| (7.7) |
Dowód
Jeżeli ![]() , to istnieje
(otwarta) kula
, to istnieje
(otwarta) kula ![]() , t.ż.
, t.ż. ![]() .
.
Dla każdego ![]() istnieje sterowanie
istnieje sterowanie ![]() , które prowadzi
, które prowadzi
![]() do
do ![]() w czasie
w czasie ![]() (punkt
(punkt ![]() jest osiągalny z
jest osiągalny z ![]() ).
).
Rozważmy zagadnienie z ustalonym sterowaniem ![]() :
:
Dla ![]() mamy
mamy ![]() dla
dla ![]() . Rozwiązanie ma postać
. Rozwiązanie ma postać
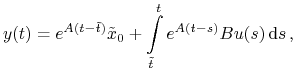 |
czyli
Dla ustalonego ![]() odwzorowanie
odwzorowanie ![]() jest liniowe ciągłe i przekształca
jest liniowe ciągłe i przekształca
![]() na
na ![]() , bo
, bo ![]() . Z twierdzenia o
odwzorowaniu otwartym (por. [34], tw. 15.4, str. 147) wynika, że
. Z twierdzenia o
odwzorowaniu otwartym (por. [34], tw. 15.4, str. 147) wynika, że ![]() przekształca
zbiory otwarte na zbiory otwarte. Stąd zbiór
przekształca
zbiory otwarte na zbiory otwarte. Stąd zbiór
jest otwarty w ![]() oraz
oraz ![]() , a zatem
, a zatem
czyli (7.7) jest spełnione, co kończy dowód lematu.
∎Twierdzenie 7.2
Dla (LA): jeżeli sterowanie ![]() jest czaso–optymalne, to
jest czaso–optymalne, to
![]() jest ekstremalne.
jest ekstremalne.
Dowód: [31], str. 61.
![]() Z lematu 7.2 wynika, że w
Z lematu 7.2 wynika, że w ![]() — momencie przybycia do celu
— momencie przybycia do celu ![]() — odpowiedź
— odpowiedź
![]() leży na brzegu zbioru osiągalnego
leży na brzegu zbioru osiągalnego ![]() . Z lematu
7.3 wynika, że jeżeli odpowiedź
. Z lematu
7.3 wynika, że jeżeli odpowiedź ![]() leży na brzegu zbioru osiągalnego
leży na brzegu zbioru osiągalnego
![]() dla pewnego
dla pewnego ![]() , to
, to
To kończy dowód.
∎Twierdzenie 7.3
Dla (LA) i ![]() następujące warunki są równoważne:
następujące warunki są równoważne:
-
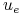 jest ekstremalne na
jest ekstremalne na ![[0,t_{e}]](wyklady/tst/mi/mi889.png) ,
, -
istnieje
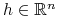 ,
, 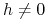 , t.ż.
, t.ż.![h^{T}e^{{-tA}}Bu_{e}(t)=\max\limits _{{v\in\Omega}}\,\Big(h^{T}e^{{-tA}}Bv\Big)\,,\qquad\mathrm{dla}\;\mathrm{p.k.}\; t\in[0,t_{e}]\,.](wyklady/tst/mi/mi835.png)
(7.8)
Dowód: [31], str. 62; [19], str. 33.
![]()
-
Dowód ,,
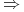 ”: załóżmy, że
”: załóżmy, że ![u_{e}\in\mathbb{U}_{m}[0,t_{e}]](wyklady/tst/mi/mi941.png) jest ekstremalne,
czyli
jest ekstremalne,
czyli![x_{e}(t):=x(t;x_{0},u_{e}(\,.\,))\,\in\,\partial\,\mathbb{K}(t;x_{0})\qquad\forall\; t\in[0,t_{e}]\,.](wyklady/tst/mi/mi903.png)
Ponieważ
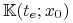 jest wypukły oraz
jest wypukły oraz
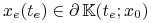 , to istnieje hiperpłaszczyzna podpierająca
, to istnieje hiperpłaszczyzna podpierająca
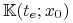 w punkcie
w punkcie 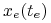 , tzn. istnieje
, tzn. istnieje 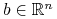 ,
, 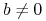 ,
t.ż.
,
t.ż.
Mamy
![x\in\mathbb{K}(t_{e};x_{0})\quad\Leftrightarrow\quad x=e^{{At_{e}}}x_{0}+\int\limits _{0}^{{t_{e}}}e^{{A(t_{e}-s)}}Bu(s)\,\mathrm{d}s\,,\quad u\in\mathbb{U}_{m}[0,t_{e}]\,.](wyklady/tst/mi/mi767.png)
Zatem
![b^{T}e^{{At_{e}}}x_{0}+b^{T}\int\limits _{0}^{{t_{e}}}e^{{A(t_{e}-s)}}Bu(s)\,\mathrm{d}s\leq b^{T}e^{{At_{e}}}x_{0}+b^{T}\int\limits _{0}^{{t_{e}}}e^{{A(t_{e}-s)}}Bu_{e}(s)\,\mathrm{d}s\quad\forall\; u\in\mathbb{U}_{m}[0,t_{e}]\,.](wyklady/tst/mi/mi922.png)
Wstawiając
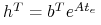 mamy
mamy 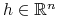 ,
, 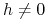 (bo macierz
(bo macierz
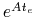 jest nieosobliwa) oraz
jest nieosobliwa) oraz![\int\limits _{0}^{{t_{e}}}h^{T}e^{{-As}}Bu(s)\,\mathrm{d}s\leq\int\limits _{0}^{{t_{e}}}h^{T}e^{{-As}}Bu_{e}(s)\,\mathrm{d}s\quad\forall\; u\in\mathbb{U}_{m}[0,t_{e}]\,.](wyklady/tst/mi/mi751.png)
(7.9) Pokażemy, że stąd wynika
![h^{T}e^{{-As}}Bu_{e}(s)=\max\limits _{{v\in\Omega}}\Big(h^{T}e^{{-As}}Bv\Big)\qquad\mathrm{dla}\;\mathrm{p.k.}\; s\in[0,t_{e}]\,.](wyklady/tst/mi/mi937.png)
(7.10) Załóżmy, że nie! Istnieje wtedy podzbiór
![\mathbb{I}\subset[0,t_{e}]](wyklady/tst/mi/mi749.png) ,
, 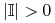 ,
t.ż.
,
t.ż.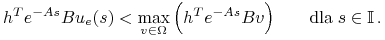
Określamy sterowanie
![\tilde{u}(t)=\left\{\begin{array}[]{cc}u_{e}(t)&t\in\mathbb{I}^{{\prime}}:=[0,t_{e}]\setminus\mathbb{I}\\
u_{{\ast}}(t)&t\in\mathbb{I}\,,\end{array}\right.](wyklady/tst/mi/mi807.png)
gdzie
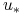 jest t.ż.
jest t.ż.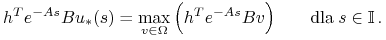
Mamy wtedy
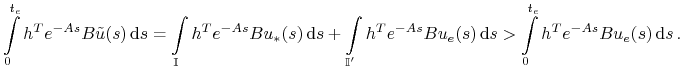
Sprzeczność z (7.9)! Zatem (7.10) jest spełnione, co kończy dowód
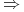 .
. -
Dowód
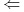 . Załóżmy, że istnieje
. Załóżmy, że istnieje 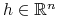 ,
, 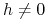 , t.ż.
, t.ż.![h^{T}e^{{-At}}Bu_{e}(t)=\max\limits _{{v\in\Omega}}\Big(h^{T}e^{{-At}}Bv\Big)\qquad\mathrm{dla}\;\mathrm{p.k.}\; t\in[0,t_{e}]\,.](wyklady/tst/mi/mi862.png)
Stąd
![\int\limits _{0}^{{t}}h^{T}e^{{-As}}Bu(s)\,\mathrm{d}s\leq\int\limits _{0}^{{t}}h^{T}e^{{-As}}Bu_{e}(s)\,\mathrm{d}s\quad\forall\; u\in\mathbb{U}_{m}[0,t_{e}]\,,](wyklady/tst/mi/mi824.png)
dla dowolnego, ale ustalonego
![t\in[0,t_{e}]](wyklady/tst/mi/mi801.png) . Wstawiając
. Wstawiając 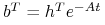 i postępując
odwrotnie jak poprzednio otrzymujemy
i postępując
odwrotnie jak poprzednio otrzymujemy
co oznacza, że
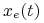 leży na brzegu
leży na brzegu 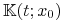 :
: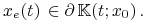
Ponieważ
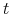 jest dowolne, więc otrzymujemy wynikanie
jest dowolne, więc otrzymujemy wynikanie 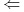 .
.
Z twierdzenia 7.2 i twierdzenie 7.3 wynika zasada maksimum Pontriagina dla liniowego zagadnienia czaso–optymalnego (Pontryagin maximum principle for linear time–optimal control) — szczególny przypadek zasady maksimum Pontriagina rozpatrywanej w rozdziale 9 — warunku koniecznego (necessary condition) dla sterowania optymalnego.
Twierdzenie 7.4
Dla (LA): jeżeli sterowanie ![]() jest czaso–optymalne, to istnieje
jest czaso–optymalne, to istnieje ![]() ,
,
![]() , t.ż.
, t.ż.
| (7.11) |
![]()
Uwaga 7.1
Każda współrzędna wektora ![]() jest funkcją analityczną zmiennej
jest funkcją analityczną zmiennej ![]() .
Stąd (por. [12] , twierdzenie 6.9, str. 199) na zwartym przedziale w
.
Stąd (por. [12] , twierdzenie 6.9, str. 199) na zwartym przedziale w ![]() jest albo tożsamościowo równa
jest albo tożsamościowo równa ![]() , albo znika tylko w skończonej liczbie punktów
, albo znika tylko w skończonej liczbie punktów ![]() .
Jeżeli zachodzi ten drugi przypadek dla każdej współrzędnej, to sterowanie
.
Jeżeli zachodzi ten drugi przypadek dla każdej współrzędnej, to sterowanie ![]() jest jednoznacznie
wyznaczone, poza skończonym (a więc miary
jest jednoznacznie
wyznaczone, poza skończonym (a więc miary ![]() ) zbiorem punktów. Wtedy sterowanie jest bang–bang
ze skończoną liczbą przełączeń (switches). Natomiast w pierwszym
przypadku sterowanie nie jest określone przez
) zbiorem punktów. Wtedy sterowanie jest bang–bang
ze skończoną liczbą przełączeń (switches). Natomiast w pierwszym
przypadku sterowanie nie jest określone przez ![]() .
Pierwszy przypadek będziemy nazywali osobliwym (singular), a drugi
normalnym (normal) — por. [24], str. 52.
.
Pierwszy przypadek będziemy nazywali osobliwym (singular), a drugi
normalnym (normal) — por. [24], str. 52.
Definicja 7.3
(LA) nazywamy normalnym (normal), jeżeli dla każdego
![]() ,
, ![]() , żadna współrzędna wektora
, żadna współrzędna wektora ![]() nie znika na zbiorze
dodatniej miary.
nie znika na zbiorze
dodatniej miary.
Każdy (LA) — normalny jest właściwy
(tzn. ![]() ).
Warunek w definicji 7.3 jest równoważny warunkowi, że żadna współrzędna nie
znika tożsamościowo.
).
Warunek w definicji 7.3 jest równoważny warunkowi, że żadna współrzędna nie
znika tożsamościowo.
Przykład 7.1
Rozpatrujemy układ RRZ, ![]() , w postaci macierzowej:
, w postaci macierzowej:
![]() ,
, ![]() ,
,
Układ jest właściwy, ale nie jest normalny.
Następujący wniosek pokazuje związek pomiędzy sterowaniami ekstremalnymi a sterowaniami bang–bang:
Twierdzenie 7.4 można zapisać w ogólnym formalizmie, który będzie później stosowany w rozdziale 9 w ogólnej sytuacji.
Definicja 7.4
Wprowadzamy hamiltonian (Hamiltonian)
| (7.13) |
gdzie ![]() ,
, ![]() .
.
Możemy wyrazić twierdzenie 7.4 w następującej postaci
Twierdzenie 7.5
Dla (LA): niech ![]() będzie sterowaniem
czaso-optymalnym z odpowiedzią
będzie sterowaniem
czaso-optymalnym z odpowiedzią
![]() . Wówczas istnieje absolutnie ciągła funkcja
. Wówczas istnieje absolutnie ciągła funkcja
![]() , t.ż.
, t.ż.
| (7.14) |
| (7.15) |
oraz
| (7.16) |
gdzie
Dowód: [19], str. 35.
![]()
Niech ![]() będzie jak w twierdzeniu 7.4. Rozważmy zagadnienie
będzie jak w twierdzeniu 7.4. Rozważmy zagadnienie
Jego rozwiązaniem jest
a zatem
Z twierdzenia 7.4 wynika, że
Zatem
![\begin{array}[]{ll}&H(w(t),x_{{\ast}}(t),u_{{\ast}}(t))=w^{T}(t)\Big(Ax_{{\ast}}(t)+Bu_{{\ast}}(t)\Big)=\\
&h^{T}e^{{-tA}}Ax_{{\ast}}(t)+h^{T}e^{{-tA}}Bu_{{\ast}}(t)=h^{T}e^{{-tA}}Ax_{{\ast}}(t)+\max\limits _{{v\in\Omega}}\Big(h^{T}e^{{-tA}}Bv\Big)=\\
&\max\limits _{{v\in\Omega}}\Big(h^{T}e^{{-tA}}Ax_{{\ast}}(t)+h^{T}e^{{-tA}}Bv\Big)=\max\limits _{{v\in\Omega}}\Big(w^{T}(t)Ax_{{\ast}}(t)+w^{T}(t)Bv\Big)=\\
&M(w(t),x_{{\ast}}(t))\,.\end{array}](wyklady/tst/mi/mi810.png) |
(7.17) |
Z definicji ![]() warunek (7.16) oraz równania (7.14) i (7.15) są
spełnione.
warunek (7.16) oraz równania (7.14) i (7.15) są
spełnione.
Definicja 7.5
Równanie (7.15) nazywa się równaniem sprzężonym (adjoint equation),
a funkcja ![]() — ko–stanem (costate).
— ko–stanem (costate).
Przykład 7.2 (wagon odrzutowy, [36], str. 29–34; [19], str. 36; [31], str. 64, 109, 111)
Rozpatrujemy układ RRZ z ![]() ,
, ![]() — por. przykłady 1.2, 2.4:
— por. przykłady 1.2, 2.4:
| (7.18) |
lub w postaci macierzowej:
-
,,W języku” twierdzenia 7.4:
Mamy
![e^{{-tA}}=I-tA=\left[\begin{array}[]{cc}1&-t\\
0&1\\
\end{array}\right]\,,\qquad\qquad h=\left[\begin{array}[]{c}h^{1}\\
h^{2}\end{array}\right]\,,\;\qquad\big(h^{1}\big)^{2}+\big(h^{2}\big)^{2}\not=0\,,](wyklady/tst/mi/mi907.png)
![h^{T}e^{{-tA}}B=[h^{1},h^{2}]\left[\begin{array}[]{cc}1&-t\\
0&1\\
\end{array}\right]\left[\begin{array}[]{c}0\\
1\end{array}\right]=[h^{1},-h^{1}t+h^{2}]\left[\begin{array}[]{c}0\\
1\\
\end{array}\right]\;=h^{2}-h^{1}t\,.](wyklady/tst/mi/mi869.png)
Układ (7.18) jest normalny!
-
,,W języku” twierdzenia 7.5:
Mamy
![w=\left[\begin{array}[]{c}w^{1}\\
w^{2}\end{array}\right]\,,](wyklady/tst/mi/mi892.png)
![H(w,x,v)=w^{T}\big(Ax+Bv\big)=[w^{1},w^{2}]\Bigg(\left[\begin{array}[]{cc}0&1\\
0&0\\
\end{array}\right]\left[\begin{array}[]{c}x^{1}\\
x^{2}\end{array}\right]+\left[\begin{array}[]{c}0\\
1\end{array}\right]v\Bigg)\,,](wyklady/tst/mi/mi855.png)
Stąd
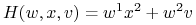
i
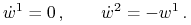
Zatem
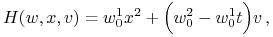
gdzie
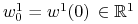 ,
, 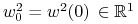 . Dla uproszczenia
zapisu nie zaznaczono w sposób jawny zależności zmiennych od
. Dla uproszczenia
zapisu nie zaznaczono w sposób jawny zależności zmiennych od 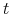 .
.
Twierdzenie 7.5 implikuje, że jeżeli
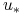 jest czaso–optymalne, to
istnieją liczby
jest czaso–optymalne, to
istnieją liczby 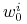 ,
, 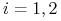 , t.ż.
, t.ż.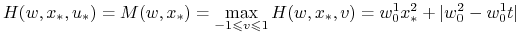
a to jest osiągane dla
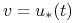 , gdzie
, gdzie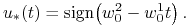
Funkcja liniowa
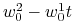 nie może być tożsamościowo
nie może być tożsamościowo 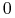 , gdyż
, gdyż 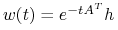 nie może znikać
tożsamościowo.
nie może znikać
tożsamościowo.
Ćwiczenie 7.1
Opisać czaso–optymalne trajektorie.
Przykład 7.3 (Zlinearyzowane równanie kątowego odchylenia od pionu z wymuszeniem, [36], str. 34–42; [31], str. 64)
Rozpatrujemy układ RRZ z ![]() ,
, ![]() :
:
| (7.19) |
lub w postaci macierzowej:
-
,,W języku” twierdzenia 7.4:
Mamy
![e^{{-tA}}=\left[\begin{array}[]{cc}\cos t&-\sin t\\
\sin t&\cos t\\
\end{array}\right]\,,\qquad h=\left[\begin{array}[]{c}h^{1}\\
h^{2}\end{array}\right]\,,\qquad\big(h^{1}\big)^{2}+\big(h^{2}\big)^{2}\not=0\,,](wyklady/tst/mi/mi818.png)
![h^{T}e^{{-tA}}B=[h^{1},h^{2}]\left[\begin{array}[]{cc}\cos t&-\sin t\\
\sin t&\cos t\\
\end{array}\right]\left[\begin{array}[]{c}0\\
1\end{array}\right]=](wyklady/tst/mi/mi910.png)
![[h^{1}\cos t+h^{2}\sin t\,,\,-h^{1}\sin t+h^{2}\cos t]\left[\begin{array}[]{c}0\\
1\\
\end{array}\right]\,,](wyklady/tst/mi/mi773.png)
stąd
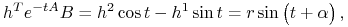
gdzie
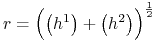 ,
,
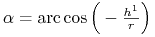 ,
,
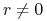 .
.Układ (7.19) jest normalny!
Z twierdzenia 7.4 wynika, że każde sterowanie optymalne
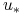 musi spełniać
musi spełniać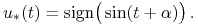
-
,,W języku” twierdzenia 7.5:
Mamy
![w=\left[\begin{array}[]{c}w^{1}\\
w^{2}\end{array}\right]\,,](wyklady/tst/mi/mi892.png)
![H(w,x,v)=w^{T}\big(Ax+Bv\big)=[w^{1},w^{2}]\Bigg(\left[\begin{array}[]{cc}0&1\\
-1&0\\
\end{array}\right]\left[\begin{array}[]{c}x^{1}\\
x^{2}\end{array}\right]+\left[\begin{array}[]{c}0\\
1\end{array}\right]v\Bigg)\,,](wyklady/tst/mi/mi918.png)
Stąd
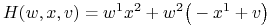
i
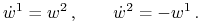
Stąd
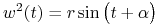 , gdzie
, gdzie 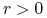 i
i 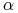 są stałymi.
są stałymi.Twierdzenie 7.5 implikuje, że jeżeli
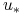 jest
czaso–optymalne, to
jest
czaso–optymalne, to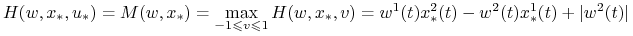
a to jest osiągane jedynie dla
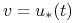 , gdzie
, gdzie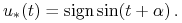
Zatem każde sterowanie czaso–optymalne jest bang–bang i okresowe o okresie
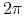 .
.
Ćwiczenie 7.2
Opisać czaso–optymalne trajektorie.
Przykład 7.4 ([31], str. 65.)
W przykładzie 7.1 rozpatrywany był układ właściwy, który nie jest normalny.
Niech ![]() . Wówczas każde ze sterowań
. Wówczas każde ze sterowań ![]() ,
, ![]() , gdzie
, gdzie
oraz
![u_{{a}}^{2}=\left\{\begin{array}[]{cc}1&0\leq t\leq a\\
0&a<t\leq 1-a\\
-1&1-a<t\leq 1\end{array}\right.\,,](wyklady/tst/mi/mi906.png) |
dla ![]() ,
,
jest czaso–optymalne z ![]() , ale tylko
, ale tylko ![]() jest bang–bang.
jest bang–bang.
Twierdzenie 7.6
Jeżeli (LA) jest normalny oraz istnieje pomyślne sterowanie (prowadzące ![]() do
do ![]() ), to istnieje jednoznaczne sterowanie czaso–optymalne. To sterowanie
jest bang–bang i kawałkami stałe.
), to istnieje jednoznaczne sterowanie czaso–optymalne. To sterowanie
jest bang–bang i kawałkami stałe.
Dowód: [31], str. 66.
![]()
Z twierdzenia 7.1 wynika istnienie. Z twierdzenia 7.4 i wniosku 7.1
wynika, że każde sterowanie czaso–optymalne jest bang–bang.
Załóżmy, że ![]() oraz
oraz ![]() są dwoma różnymi sterowaniami czaso–optymalnymi bang–bang.
Wówczas sterowanie
są dwoma różnymi sterowaniami czaso–optymalnymi bang–bang.
Wówczas sterowanie ![]() jest też czaso–optymalne, ale nie jest
bang–bang. Otrzymujemy sprzeczność: zatem sterowanie czaso–optymalne jest jednoznaczne.
jest też czaso–optymalne, ale nie jest
bang–bang. Otrzymujemy sprzeczność: zatem sterowanie czaso–optymalne jest jednoznaczne.
Sterowanie czaso–optymalne jest kawałkami stałe, gdyż każda współrzędna zmienia wartość tylko wtedy,
gdy ta sama współrzędna ![]() przyjmuje wartość
przyjmuje wartość ![]() , a to może zdarzyć się tylko w
skończonej liczbie punktów odcinka
, a to może zdarzyć się tylko w
skończonej liczbie punktów odcinka ![]() .
.
Definicja 7.6
Niech ![]() będzie ustalone,
będzie ustalone, ![]() oraz
oraz ![]() .
Jeżeli
.
Jeżeli
| (7.20) |
dla każdego ![]() i każdego
i każdego ![]() , t.ż.
, t.ż.
to odpowiedź z ![]() do
do ![]() jest
jednoznaczna (unique).
jest
jednoznaczna (unique).
Twierdzenie 7.7
Załóżmy, ze macierz ![]() nie ma żadnej kolumny złożonej z samych
nie ma żadnej kolumny złożonej z samych ![]() ,
, ![]() i niech
i niech ![]() .
Wówczas następujące warunki są równoważne
.
Wówczas następujące warunki są równoważne
-
sterowanie prowadzące
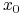 do
do 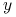 w czasie
w czasie 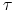 jest jednoznaczne,
jest jednoznaczne, -
odpowiedź z
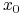 do
do 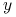 w czasie
w czasie 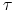 jest
jednoznaczna,
jest
jednoznaczna, -
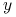 jest ekstremalnym punktem
jest ekstremalnym punktem 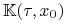 .
.
Dowód: [31], str. 69–71.![]()
Dalej w tym rozdziale będziemy zakładać, że macierz ![]() nie ma żadnej kolumny złożonej z samych
nie ma żadnej kolumny złożonej z samych
![]() . Nie zmniejsza to ogólności!
. Nie zmniejsza to ogólności!
Definicja 7.7
Zbiór ![]() jest ściśle wypukły jeżeli
jest ściśle wypukły jeżeli
dla każdych dwóch punktów ![]() .
.
Twierdzenie 7.8 (Geometryczna charakteryzacja (LA) normalnych)
(LA) jest normalny na ![]()
![]()
![]() jest
ściśle wypukły dla pewnego
jest
ściśle wypukły dla pewnego ![]() .
.
Dowód: [31], str. 71.![]()
Twierdzenie 7.9 (Analityczna charakteryzacja (LA) normalnych)
(LA) jest normalny na ![]()
![]()
![]() są liniowo niezależnymi wektorami w
są liniowo niezależnymi wektorami w ![]() , dla każdej kolumny
, dla każdej kolumny ![]() macierzy
macierzy ![]() ,
, ![]() .
.
Dowód: [31], str. 72.![]()
Podsumowaniem jest następujący wniosek:
Wniosek 7.2
Dla (LA) normalnego: istnieje otoczenie ![]() punktu
punktu ![]() , t.ż. każdy punkt
, t.ż. każdy punkt
![]() może być doprowadzony do
może być doprowadzony do ![]() jednoznacznym sterowaniem czaso-optymalnym
bang–bang i kawałkami stałym. Jeżeli dodatkowo
jednoznacznym sterowaniem czaso-optymalnym
bang–bang i kawałkami stałym. Jeżeli dodatkowo ![]() , dla każdej wartości własnej
, dla każdej wartości własnej
![]() macierzy
macierzy ![]() , to
, to ![]() .
.
Twierdzenie 7.10
Dla (LA) normalnego:
jeżeli każda wartość własna (eigenvalue) macierzy ![]() jest rzeczywista,
jest rzeczywista,
to każda współrzędna każdego sterowania czaso–optymalnego ma
co najwyżej ![]() przełączeń.
przełączeń.
Poniższe twierdzenie formułuje warunek dostateczny — odwrotność zasady maksimum:
Twierdzenie 7.11
Dla (LA) właściwego: każde (pomyślne) sterowanie ![]() , prowadzące
, prowadzące ![]() do
do ![]() w czasie
w czasie
![]() i spełniające
i spełniające
![\begin{array}[]{l}\mathrm{dla}\;\mathrm{pewnego}\; h\in{\mathbb{R}}^{n}\,,\; h\not=0\,:\\
h^{T}e^{{-tA}}Bu_{{\ast}}(t)=\max\limits _{{v\in\Omega}}(h^{T}e^{{-tA}}Bv)\\
\mathrm{dla}\;\mathrm{p.k.}\; t\in\,]\, 0,\tau\,[\,,\end{array}](wyklady/tst/mi/mi829.png) |
(7.21) |
jest czaso–optymalne na ![]() .
.
Dowód: [31], str. 77.![]()




