9. Zasada Maksimum Pontriagina

Poprzedni rozdział 8 dotyczył warunku wystarczającego (sufficient condition) istnienia sterowania optymalnego. Natomiast w tym rozdziale 9 sformułujemy warunek konieczny (necessary condition) dla optymalnego sterowania — zwany zasadą maksimum Pontriagina (Pontryagin Maximum Principle). Zasada ta pozwala wyznaczyć optymalne sterowania i optymalne trajektorie — por. przykłady 7.2, 7.3.

Analogia: Minimum funkcji z więzami (ograniczeniami, constraints).

Rozważamy gładkie funkcje $\, h\,:\;\mathbb{D}\to{\mathbb{R}}^{1}\,$ , $\, g^{j}\,:\:\mathbb{D}\to{\mathbb{R}}^{1}\,$ , $j=1,\ldots,l$ , $l<n$ ,

gdzie $\mathbb{D}$ jest niepustym obszarem w ${\mathbb{R}}^{n}$ . Badamy istnienie minimum funkcji $h$ na hiperpowierzchni (hypersurface)

$\mathbb{S}=\big\{ x\in{\mathbb{R}}^{n}\,:\; g(x)=0\big\}\,.$

Jeżeli $x_{{\ast}}\in\mathbb{D}$ jest punktem, w którym $h$ ma (lokalne) minimum na hiperpowierzchni $\mathbb{S}$ , to istnieją liczby (mnożniki Lagrange'a (Lagrange multipliers)) $w=(w^{1},w^{2},\ldots,w^{l})$ , t.ż. $x_{{\ast}}\in\mathbb{D}$ , $w\in{\mathbb{R}}^{l}$ jest rozwiązaniem $n+l$ równań:

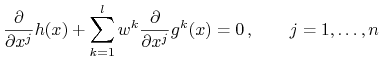$\frac{\partial}{\partial x^{j}}h(x)+\sum\limits _{{k=1}}^{l}w^{k}\frac{\partial}{\partial x^{j}}g^{k}(x)=0\,,\qquad j=1,\ldots,n$

$g^{k}(x)=0\,,\qquad k=1,\ldots,l$

czyli

$\mathrm{grad}_{x}\, h(x_{{\ast}})=-\mathrm{grad}_{x}\,\Big(w^{T}g(x_{{\ast}})\Big)\qquad g(x_{{\ast}})=0\,,$

zatem wektor $\,\mathrm{grad}_{x}h(x_{{\ast}})\,$ jest prostopadły do hiperpłaszczyzny stycznej do hiperpowierzchni $\mathbb{S}$ w punkcie $x_{{\ast}}$ , czyli jest normalny do $\mathbb{S}$ w $x_{{\ast}}$ .

W tym rozdziale nie zakładamy żadnych ograniczeń na sterowania, czyli $\Omega={\mathbb{R}}^{m}$ .

Rozpatrujemy najpierw zagadnienie Lagrange'a (L) dla ustalonego punktu końcowego (I) — por. rozdział 6. Zakładamy, że $\mathfrak{f}^{0}$ jest ciągła względem $(x,u)$ oraz różniczkowalna w sposób ciągły względem $x$ .

Problem 9.1

Mamy zadane punkty $x_{0}\,,\; x_{1}\,\in{\mathbb{R}}^{n}$ , $x_{0}\not=x_{1}$ . Wśród dopuszczalnych sterowań $u\in{\mathbb{U}}_{m}$ , o tej własności, że rozwiązanie $x(t)=x(t;x_{0},\,{u(\,.\,)}\,)$ zagadnienia

${\dot{x}}=f(x,u)\,,\qquad x(0)=x_{0}\,,$

przechodzi przez $x_{1}$ dla ${t_{1}}>0$ , tzn. $x({t_{1}})=x_{1}$ , znaleźć to, dla którego

${\mathfrak{C}}[u]=\int\limits _{{0}}^{{{{t_{1}}}}}\mathfrak{f}^{0}(x(t),u(t))\,\mathrm{d}t\,,$

przyjmuje najmniejszą wartość.

Definicja 9.1

Sterowanie $u$ , o którym mowa w zagadnieniu 9.1, nazywamy sterowaniem optymalnym (optimal control), a odpowiednią trajektorię ${x}={x}(t)$ — trajektorią optymalną (optimal trajectory).

Zauważmy, że jeżeli sterowanie $u=u(t)$ , $0\leq t\leq{t_{1}}$ , prowadzi $x_{0}$ do $x_{1}$ z wartością $\mathfrak{C}[u]=J$ , to sterowanie $\tilde{u}=u(t+\tau)$ , $-\tau\leq t\leq{t_{1}}-\tau$ także prowadzi $x_{0}$ do $x_{1}$ z wartością $\mathfrak{C}[\tilde{u}]=J$ . To pozwala przyjąć chwilę początkową, jako $t=0$ .

Każdy kawałek trajektorii optymalnej jest też trajektorią optymalną:

Uwaga 9.1

Jeżeli $u=u(t)$ , $0\leq t\leq{t_{1}}$ , jest sterowaniem optymalnym prowadzącym $x_{0}$ do $x_{1}$ , $x(t)=x(t;x_{0},{u(\,.\,)})$ — trajektorią optymalną oraz $0\leq\tau _{1}\leq\tau _{2}\leq{t_{1}}$ , to sterowanie $u\Big|_{{[\tau _{1},\tau _{2}]}}$ jest optymalnym sterowaniem prowadzącym $x(\tau _{1})$ do $x(\tau _{2})$ oraz $x\Big|_{{[\tau _{1},\tau _{2}]}}$ jest trajektorią optymalną.

Dowód: por. [36], str. 22; [31], str. 118.

$\quad$

Niech wartości $\mathfrak{C}[u]$ na odcinkach $[0,\tau _{0}]$ , $[\tau _{0},\tau _{1}]$ , $[\tau _{1},{t_{1}}]$ będą oznaczone przez $J_{1}$ , $J_{2}$ i $J_{3}$ , odpowiednio. Wówczas wartość $\mathfrak{C}[u]$ na odcinku $[0,{t_{1}}]$ , to $J=J_{1}+J_{2}+J_{3}$ . Jeżeli sterowanie $u\Big|_{{[\tau _{1},\tau _{2}]}}$ nie byłoby optymalne, to istniałoby sterowanie $\tilde{u}$ prowadzące $x(\tau _{0})$ do $x(\tau _{1})$ z wartością $\mathfrak{C}[\tilde{u}]={J}_{2}^{{\ast}}$ , gdzie $J_{2}^{{\ast}}<J_{2}$ . Zatem istniałoby sterowanie prowadzące $x_{0}$ do $x_{1}$ z wartością $J_{1}+J_{2}^{{\ast}}+J_{3}<J$ , co jest sprzeczne z optymalnością sterowania $u$ .

∎

Dla zagadnienia Lagrange'a, zadanego sterowania $u$ i odpowiedzi $x$ określamy

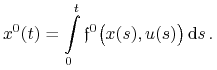$x^{0}(t)=\int\limits _{{0}}^{t}\mathfrak{f}^{0}\big(x(s),u(s)\big)\,\mathrm{d}s\,.$

Jeżeli $u$ jest pomyślne, to $x({{t_{1}}})=x_{1}$ , dla pewnego ${{t_{1}}}\geq 0$ i odpowiedni koszt to $x^{0}({{t_{1}}})$ . Gdy $u$ jest optymalne, to $x^{0}({{t_{1}}})$ jest najmniejsze.

Określamy wektor $(n+1)$ –wymiarowy $\mathbf{x}(t)=\big(x^{0}(t),x^{T}(t)\big)^{T}$ oraz

$\mathbf{f}(t,\mathbf{x})=\big(\mathfrak{f}^{0},f^{T}\big)^{T}(t,\mathbf{x})\,.$

Zakładamy, że $f$ oraz $\mathfrak{f}^{0}$ są ciągłe względem $(x,u)$ oraz różniczkowalne w sposób ciągły względem $x$ .

Zagadnienie 9.1 można sformułować w następującej, równoważnej postaci:

Problem 9.2

Niech $x_{0}\in{\mathbb{R}}^{n}$ oraz $\Pi$ będzie prostą w ${\mathbb{R}}^{{n+1}}$ :

$\Pi=\Big\{\,\big[y,x_{1}^{T}\big]^{T}\in{\mathbb{R}}^{{n+1}}\,:\; y\in{\mathbb{R}}^{1}\,\Big\}\,,$

gdzie $x_{1}\in{\mathbb{R}}^{n}$ jest ustalonym punktem. Wśród sterowań $u\in{\mathbb{U}}_{m}$ , o tej własności, że rozwiązanie $\mathbf{x}(t)=\mathbf{x}\big(t;\mathbf{x}_{0},\,{u(\,.\,)}\,\big)$ zagadnienia

${\dot{\mathbf{x}}}(t)={\mathbf{f}}\big({\mathbf{x}}(t),u(t)\big)\qquad\mathrm{p.w.}\,,$

(9.1)

${\mathbf{x}}(0)=\mathbf{x}_{0}=\big[0,x_{0}^{T}\big]^{T}\in{\mathbb{R}}^{{n+1}}\,,$

przecina prostą $\Pi$ , znaleźć to, dla którego punkt $\mathbf{x}_{1}=\big[x_{1}^{0},x_{1}^{T}\big]^{T}$ przecięcia z prostą $\Pi$ ma najmniejszą współrzędną $x_{1}^{0}$ .

Podobnie jak w definicji 9.1:

Definicja 9.2

Sterowanie $u$ , o którym mowa w zagadnieniu 9.2, nazywamy sterowaniem optymalnym (optimal control), a odpowiednią trajektorię $\mathbf{x}=\mathbf{x}(t)$ — trajektorią optymalną (optimal trajectory).

Wprowadzamy sprzężenie linearyzacji (adjoint to the linearization):

dla zadanego sterowania $u$ i odpowiedzi $\mathbf{x}$ rozważamy $(n+1)$ –wymiarowe zagadnienie zlinearyzowane

${\dot{\mathbf{w}}}(t)=-\Big[{\mathbf{f}}_{{\mathbf{x}}}\big(x(t),u(t)\big)\Big]^{T}\,\mathbf{w}(t)\qquad\mathrm{p.w.}\,;$

(9.2)

Rozwiązanie tego zagadnienia nazywa się rozszerzonym ko-stanem (extended costate; adjoint variable; Lagrange multiplier);

$\mathbf{f}_{{\mathbf{x}}}\big(x(t),u(t)\big)$ jest macierzą Jacobiego $\mathbf{f}$ względem $\mathbf{x}$ ,

$\mathbf{f}_{{\mathbf{x}}}\big(x(t),u(t)\big)\,=\left[\frac{\partial\,{\mathbf{f}}^{i}}{\partial\,{\mathbf{x}}^{j}}\right]\,=\,\left[\begin{array}[]{cccc}0&\frac{\partial\, f^{0}}{\partial\, x^{1}}&\ldots&\frac{\partial\, f^{0}}{\partial\, x^{n}}\\ 0&\frac{\partial\, f^{1}}{\partial\, x^{1}}&\ldots&\frac{\partial\, f^{1}}{\partial\, x^{n}}\\ .&&&\\ .&&&\\ .&&&\\ 0&\frac{\partial\, f^{n}}{\partial\, x^{1}}&\ldots&\frac{\partial\, f^{n}}{\partial\, x^{n}}\\ \end{array}\right]$

(w pierwszej kolumnie są same zera, gdyż żadna z $\mathbf{f}^{i}$ nie zależy jawnie od $x^{0}$ ).

Zlinearyzowane równanie opisuje ewolucję wektora stycznego wzdłuż krzywej wyznaczonej przez rozwiązanie zagadnienia wyjściowego. Sprzężone równanie zlinearyzowane opisuje ewolucję wektorów prostopadłych — leżących w $n$ -wymiarowej hiperpłaszczyźnie.

Dla zadanego $(\mathbf{x},u)$ , rozważamy ko-stan i rzeczywistą funkcję (Hamiltonian)

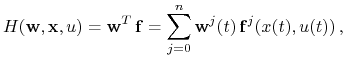$H(\mathbf{w},\mathbf{x},u)={\mathbf{w}}^{T}\,{\mathbf{f}}=\sum\limits _{{j=0}}^{n}\mathbf{w}^{j}(t)\,\mathbf{f}^{j}(x(t),u(t))\,,$

$H$ nie zależy od $x^{0}$ , gdyż $f^{j}$ nie zależą od $x^{0}$ :

$H({\mathbf{w}},{\mathbf{x}},u)=H({\mathbf{w}},x,u)\,.$

Mamy

$\dot{\mathbf{x}}={\mathrm{grad}}_{{\mathbf{w}}}H({\mathbf{w}},x,u)=\Bigg[\frac{\partial\, H}{\partial\, w^{0}},\frac{\partial\, H}{\partial\, w^{1}},\ldots,\frac{\partial\, H}{\partial\, w^{n}}\Bigg]^{T}\,,\qquad{\rm p.w.}$

(9.3)

${\dot{\mathbf{w}}}=-{\mathrm{grad}}_{{\mathbf{x}}}H({\mathbf{w}},x,u)=-\Bigg[{0},\frac{\partial\, H}{\partial\, x^{1}},\ldots,\frac{\partial\, H}{\partial\, x^{n}}\Bigg]^{T}\,,\qquad{\rm p.w.}\,,$

(9.4)

gdzie równanie (9.3), to inny zapis równania (9.1), a równanie (9.4), to inny zapis równania (9.2). Zatem równanie (9.3), to wyjściowy układ RRZ. W układzie tym nie pojawia się ko–stan $\mathbf{w}$ .

Definicja 9.3

$M({\mathbf{w}},x)=\sup\limits _{{v\in\Omega}}H({\mathbf{w}},x,v)$

Twierdzenie 9.1 (Zasada maksimum Pontriagina (Pontryagin Maximum Principle) dla zagadnienia ustalonego punktu końcowego (fixed–end–point) — (I))

Rozważamy rozszerzone zagadnienie sterowania

$\dot{\mathbf{x}}^{j}=\frac{\partial}{\partial{\mathbf{w}}^{j}}H(\mathbf{w},x,u)\,,\qquad j=0,1,\ldots,n$

z $u\in{{\mathbb{U}}}_{m}$ . Jeżeli $u_{{\ast}}$ jest optymalne na $[0,{t_{1}}]$ z odpowiedzią $\mathbf{x}_{{\ast}}$ , to istnieje absolutnie ciągła funkcja $\mathbf{w}$ spełniająca

${\dot{\mathbf{w}}}^{j}=-\frac{\partial}{\partial\mathbf{x}^{j}}H({\mathbf{w}},x_{{\ast}},u_{{\ast}})\,,\qquad j=0,1,\ldots,n\,,\qquad\mathrm{p.w.}\;\mathrm{na}\;[0,{{t_{1}}}]$

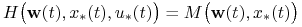(i) $H\big({\mathbf{w}}(t),x_{{\ast}}(t),u_{{\ast}}(t)\big)=M\big({\mathbf{w}}(t),x_{{\ast}}(t)\big)$ p.w. na $[0,{{t_{1}}}]$
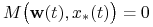(ii) $M\big({\mathbf{w}}(t),x_{{\ast}}(t)\big)=0$ na $[0,{{t_{1}}}]$
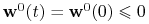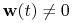(iii) $\mathbf{w}^{0}(t)=\mathbf{w}^{0}(0)\leq 0$ oraz ${\mathbf{w}}(t)\not=0$ na $[0,{{t_{1}}}]$ .

Dowód: [36], rozdział 2, §10–15; [31], str. 134–146; [19], str. 112–124; [6], str. 304–340. $\;\clubsuit$

Zasada określa warunek konieczny (necessary condition) sterowania optymalnego: jeżeli $u_{{\ast}}$ jest optymalne dla zagadnienia (I), to istnieje para ${\mathbf{x}}_{{\ast}},{\mathbf{w}}$ , t.ż. dla p.k. $t\in[0,{t_{1}}]$

${\dot{\mathbf{x}}}=\mathrm{grad}_{{\mathbf{w}^{j}}}H(\mathbf{w},x_{{\ast}},u_{{\ast}})\,,\qquad\quad\mathrm{oraz}\qquad\quad H(\mathbf{w},x_{{\ast}},v)\leq 0\,,\quad\forall\quad v\in{\Omega}\,,$

oraz równość jest osiągana dla $v=u_{{\ast}}(t)$ — oczywiście może być również osiągana dla innych wartości $v$ .

Równość w (i) (bez ,,p.w.”) zachodzi, w każdym punkcie prawostronnej, lub lewostronnej ciągłości sterowania $u$ — por. [31], Lemma 1, str. 110.

Uwaga 9.2

Zasada maksimum Pontriagina dla swobodnego punktu końcowego — zagadnienie (III) — rozdział 6. Jeżeli czas końcowy ${t_{1}}>0$ jest ustalony, a punkt końcowy $x_{1}$ nie jest zadany, to twierdzenie 9.1 należy uzupełnić o warunek transwersalności (transversality condition) — por. (9.6):

$\mathbf{w}^{j}({t_{1}})=0\,,\qquad j=1,\ldots,n\,.$

(9.5)

Z twierdzenia 9.1 można wyprowadzić warunek konieczny dla sterowania czaso–optymalnego. Niech $w=(w^{1}\ldots,w^{n})$ . Mamy

$\mathfrak{f}^{0}\equiv 1\,,\qquad x^{0}(t)=t$

oraz

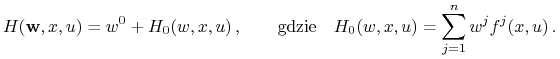$H(\mathbf{w},x,u)={w}^{0}+H_{0}(w,x,u)\,,\qquad\mathrm{gdzie}\quad H_{0}(w,x,u)=\sum\limits _{{j=1}}^{{n}}w^{j}f^{j}(x,u)\,.$

Wówczas mamy

$x^{j}=\;\frac{\partial H_{0}}{\partial w^{j}}\,,\qquad w^{j}=-\frac{\partial H_{0}}{\partial x^{j}}\,,\qquad j=1,\ldots,n\,.$

Niech

$M_{0}(w,x)=\sup\limits _{{v\in\Omega}}H_{0}(w,x,v)\,.$

Z zależności

$H_{0}(w,x,u)=H(\mathbf{w},x,u)-w^{0}$

otrzymujemy

$M_{0}(w,x)=M(\mathbf{w},x)-w^{0}$

a zatem

$H_{0}(w(t),x(t),u(t))=M_{0}(w(t),x(t))=-w^{0}\geq 0\,.$

Twierdzenie 9.2 (Zasada maksimum Pontriagina dla sterowania czaso-optymalnego)

Rozważamy zagadnienie

$\dot{x}^{j}=\frac{\partial}{\partial{w}^{j}}H_{0}(w,x,u)\,,\qquad j=1,\ldots,n$

z $u\in{{\mathbb{U}}}_{m}$ . Jeżeli $u_{{\ast}}$ jest czaso–optymalne z odpowiedzią $x_{{\ast}}$ , to istnieje absolutnie ciągła funkcja $\mathbf{w}$ spełniająca

$\dot{w}^{j}=-\frac{\partial}{\partial{x}^{j}}H_{0}(w,x_{{\ast}},u_{{\ast}})\,,\qquad j=1,\ldots,n\,,\qquad\mathrm{p.w.}\;\mathrm{na}\;[0,{{t_{1}}}]$

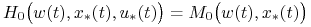(i) $H_{0}\big(w(t),x_{{\ast}}(t),u_{{\ast}}(t)\big)=M_{0}\big(w(t),x_{{\ast}}(t)\big)$ p.w. na $[0,{{t_{1}}}]$
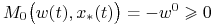(ii) $M_{0}\big(w(t),x_{{\ast}}(t)\big)=-w^{0}\geq 0$ na $[0,{{t_{1}}}]$
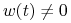(iii) $w(t)\not=0$ na $[0,{{t_{1}}}]$ .

Przykład 9.1 (wagon odrzutowy, [36], str. 29–34; [19], str. 36, [31], str. 109, 111)

Por. przyklad 1.2, 2.4, 7.2. Przykład ten jest powtórzeniem przykładu 7.2 ,,w języku” twierdzenia 9.1. Niech $\Omega=[-1,1]$ .

$\mathbf{x}=\left[\begin{array}[]{c}x^{0}\\ x^{1}\\ x^{2}\end{array}\right]\,,\qquad{x}=\left[\begin{array}[]{c}x^{1}\\ x^{2}\end{array}\right]\,,\qquad{\mathfrak{C}}[u]=\int\limits _{0}^{{{{t_{1}}}}}1\,{\rm d}t={{t_{1}}}\,,$

$\dot{x}^{0}=1\,,\qquad\dot{x}^{1}=x^{2}\,,\qquad\dot{x}^{2}=u\,,\qquad\mathbf{f}(x,u)=\left[\begin{array}[]{c}1\\ x^{2}\\ u\end{array}\right]\,,$

${\mathbf{f}}_{{\mathbf{x}}}=\left[\begin{array}[]{ccc}0&0&0\\ 0&0&1\\ 0&0&0\end{array}\right]\,,\qquad{\mathbf{w}}=\left[\begin{array}[]{c}w^{0}\\ w^{1}\\ w^{2}\end{array}\right]\,,$

$\dot{w}^{0}=\dot{w}^{1}=0\,,\qquad\dot{w}^{2}=-w^{1}\,,$

$H(\mathbf{w},x,v)=\mathbf{w}^{T}\mathbf{f}(x,v)=w^{0}_{0}+w^{1}_{0}x^{2}+\Big(w^{2}_{0}-w^{1}_{0}t\Big)v\,,$

Z twierdzenia 9.1: jeżeli $u_{{\ast}}$ jest czaso–optymalne, to istnieją liczby $w^{i}_{0}$ , $i=0,1,2$ , t.ż.

$H(\mathbf{w},x_{{\ast}},v)\leq 0\quad\forall\; v\in[-1,1]\,,\qquad H(\mathbf{w},x_{{\ast}},v)=0\quad{\rm p.w.}\quad{\rm dla}\; v=u_{{\ast}}(t)\,,$

$M(\mathbf{w},x_{{\ast}})=\sup\limits _{{-1\leq v\leq 1}}H(\mathbf{w},x_{{\ast}},v)=w^{0}_{0}+w^{1}_{0}x^{2}_{{\ast}}(t)+\Big|w^{2}_{0}-w^{1}_{0}\, t\Big|$

a to jest osiągane jedynie dla

$u(t)=\mathrm{sign}\Big(w^{2}_{0}-w^{1}_{0}\, t\Big)\,.$

Funkcja liniowa $w^{2}_{0}-w^{1}_{0}t$ jest albo tożsamościowo $0$ , albo zeruje się w co najwyżej jednym punkcie. Zatem każde czaso–optymalne sterowanie jest p.w. albo tożsamościowo $0$ , albo bang–bang. Nie może jednak być tożsamościowo $0$ , gdyż byłoby wtedy $w^{1}_{0}=w^{2}_{0}=0$ i mielibyśmy $w^{0}_{0}\not=0$ ( $\mathbf{w}$ nie może znikać), co by dawało $H=w^{0}_{0}\not=0$ , a zatem $M=w^{0}_{0}\not=0$ , co byłoby sprzeczne z twierdzeniem 9.1 (ii); por. przykład 7.2.

Rozważmy przypadek, gdy punkt końcowy $x_{1}$ nie jest ustalony, lecz należy do zadanego zbioru $\mathbb{S}_{1}$ , o którym zakładamy, że jest $l$ –wymiarową gładką rozmaitością (manifold; por. [12], str. 64) w ${\mathbb{R}}^{n}$ , $l<n$ — zagadnienie (II). Możemy sformułować następujące twierdzenie

Twierdzenie 9.3 (Zasada maksimum Pontriagina dla zagadnienia dla punktu końcowego z zadanej rozmaitości — (II))

Rozważamy rozszerzone zagadnienie sterowania

$\dot{\mathbf{x}}^{j}=\frac{\partial}{\partial{\mathbf{w}}^{j}}H(\mathbf{w},\mathbf{x},u)\,,\qquad j=0,1,\ldots,n$

z $u\in{{\mathbb{U}}}_{m}$ . Jeżeli $u_{{\ast}}$ jest optymalne na $[0,{t_{1}}]$ z odpowiedzią $\mathbf{x}_{{\ast}}$ , to istnieje absolutnie ciągła funkcja $\mathbf{w}$ spełniająca

${\dot{\mathbf{w}}}^{j}=-\frac{\partial}{\partial\mathbf{x}^{j}}H({\mathbf{w}},\mathbf{x}_{{\ast}},u_{{\ast}})\,,\qquad j=0,1,\ldots,n\,,\qquad\mathrm{p.w.}\quad\mathrm{na}\;[0,{{t_{1}}}]$

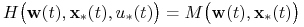(i) $H\big({\mathbf{w}}(t),\mathbf{x}_{{\ast}}(t),u_{{\ast}}(t)\big)=M\big({\mathbf{w}}(t),\mathbf{x}_{{\ast}}(t)\big)$ p.w. na $[0,{{t_{1}}}]$
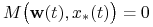(ii) $M\big({\mathbf{w}}(t),x_{{\ast}}(t)\big)=0$ na $[0,{{t_{1}}}]$
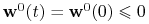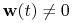(iii) $\mathbf{w}^{0}(t)=\mathbf{w}^{0}(0)\leq 0$ oraz ${\mathbf{w}}(t)\not=0$ na $[0,{{t_{1}}}]$

oraz spełniony jest warunek transwersalności (transversality (transversal $=$ orthogonal to the tangent space))

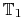(iv) wektor $w({t_{1}})=[w^{1}({t_{1}}),\ldots,w^{n}({t_{1}})]^{T}$ jest prostopadły do przestrzeni stycznej (tangent space) $\mathbb{T}_{1}$ do rozmaitości 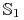$\mathbb{S}_{1}$ w punkcie $x({t_{1}})$ :

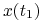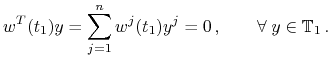
$w^{T}({t_{1}})y=\sum\limits _{{j=1}}^{n}w^{j}({t_{1}})y^{j}=0\,,\qquad\forall\; y\in\mathbb{T}_{1}\,.$ (9.6)

Dowód: [36], rozdział 2, §16; [6], str. 306–344; [28], Chapter 5, [20], rozdziały 12 i 13. $\;\clubsuit$

Uwaga 9.3

W przypadku zagadnienia swobodnego punktu końcowego — (III) — warunek transwersalności (9.6) przyjmuje postać (9.5):

$w({t_{1}})=0\,.$

Przykład 9.2 (wagon odrzutowy, por. przykład 9.1, [36], str. 51-61; [31], str. 125)

Rozważamy układ równań z przykładu 9.1 z $\Omega=[-1,1]$ , jednakże cel określamy jako

${\mathcal{T}}(t)\equiv\mathbb{S}=\Big\{\left[\begin{array}[]{c}x^{1}\\ x^{2}\end{array}\right]\in{\mathbb{R}}^{2}\,,\qquad x^{1}=0\Big\}\,,$

czyli jesteśmy zainteresowani osiągnięciem położenia $x^{1}=0$ z dowolną prędkością $x^{2}\in{\mathbb{R}}^{1}$ .

Wektor styczny (w dowolnym punkcie $(0,x_{2})$ ) do $\mathbb{S}$ ma postać

$\alpha=\left[\begin{array}[]{c}0\\ \alpha^{2}\end{array}\right]\,,$

gdzie $\alpha^{2}\not=0$ . Warunek transwersalności przyjmuje więc postać

$w^{T}({t_{1}})\alpha=0\,,$

(9.7)

skąd $w^{2}({t_{1}})=0$ . Ponieważ (por. przykład 9.1)

$w^{2}(t)=w^{2}_{0}-w^{1}_{0}t\,,$

to z (9.7) wynika, że $w^{2}(t)$ na odcinku $[0,{t_{1}}]$ nie zmienia znaku. Zatem każde czaso–optymalne sterowanie jest stałe i równe albo $-1$ , albo $1$ , bez przełączeń. Zatem przez każdy punkt początkowy $x_{0}$ przechodzą tylko dwie trajektorie, które mogą być optymalne (dla $u\equiv-1$ i $u\equiv 1$ ).

Jeżeli $x_{0}^{1}>0$ i punkt początkowy leży powyżej dolnej części trajektorii przechodzącej przez $0$ , to jedynie trajektoria dla $u\equiv-1$ prowadzi do $\mathbb{S}$ . Natomiast, gdy $x_{0}^{1}>0$ i punkt początkowy leży na, lub poniżej dolnej części trajektorii przechodzącej przez $0$ , to do celu prowadzi zarówno trajektoria z $u\equiv-1$ , jak i $u\equiv 1$ . Mamy więc dwie trajektorie podlegające zasadzie maksimum. Można jednak pokazać (ćwiczenie), że czas dojścia do $\mathbb{S}$ w obu przypadkach jest różny i optymalnym sterowaniem jest $u\equiv-1$ . Analogicznie dla $x_{0}^{1}<0$ optymalnym sterowaniem jest $u\equiv 1$ . Można więc zsyntetyzować optymalne sterowanie (synthesize the optimal control) wprowadzając

$v(x^{1},x^{2})=\left\{\begin{array}[]{ccc}+1&\mathrm{dla}&x^{1}<0\\ -1&\mathrm{dla}&x^{1}>0\end{array}\right.$

i rozważając układ

$\begin{array}[]{ccc}\dot{x}^{1}&=&x^{2}\\ \dot{x}^{2}&=&v(x^{1},x^{2})\end{array}$

otrzymujac wszystkie optymalne trajektorie.

Analogia: Zagadnienie minimum rzeczywistej, gładkiej funkcji $h$ na obszarze $\mathbb{D}\in{\mathbb{R}}^{n}$ .

Warunek konieczny (the necessary condition): Jeżeli punkt $x_{{\ast}}\in\mathbb{D}$ jest minimum funkcji $h$ , to

$\frac{\partial}{\partial x^{j}}h(x_{{\ast}})=0\,,\qquad j=1,\ldots,n\,.$

Wprowadzając $g(t)=h(x_{{\ast}}+t\alpha)$ , gdzie $\alpha\in{\mathbb{R}}^{n}$ , $|\alpha|=1$ , otrzymujemy

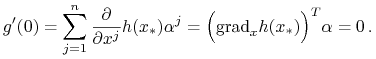$g^{{\prime}}(0)=\sum\limits _{{j=1}}^{n}\frac{\partial}{\partial x^{j}}h(x_{{\ast}})\alpha^{j}=\Big(\mathrm{grad}_{x}h(x_{{\ast}})\Big)^{T}\alpha=0\,.$

Mamy

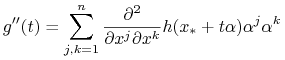$g^{{\prime\prime}}(t)=\sum\limits _{{j,k=1}}^{n}\frac{\partial^{2}}{\partial x^{j}\partial x^{k}}h(x_{{\ast}}+t\alpha)\alpha^{j}\alpha^{k}$

Warunkiem wystarczającym (sufficient condition) minimum jest

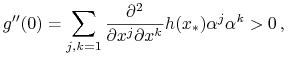$g^{{\prime\prime}}(0)=\sum\limits _{{j,k=1}}\frac{\partial^{2}}{\partial x^{j}\partial x^{k}}h(x_{{\ast}})\alpha^{j}\alpha^{k}>0\,,$

czyli macierz

$\left[\begin{array}[]{c}\frac{\partial^{2}}{\partial x^{j}\partial x^{k}}h(x_{{\ast}})\end{array}\right]_{{j,k=1,\ldots,n}}$

jest dodatnio określona.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Teoria sterowania