Zagadnienia
10. Jak szukać miar niezmienniczych
10.1. Twierdzenie Kryłowa- Bogoliubowa
Rozważmy przekształcenie mierzalne względem ![]() - ciała
- ciała ![]() ,
, ![]() .
Czy
.
Czy ![]() ma jakąś miarę niezmienniczą określoną na
ma jakąś miarę niezmienniczą określoną na ![]() ?
Otóż- nie musi tak być. Rozważmy
?
Otóż- nie musi tak być. Rozważmy
Przykład 10.1
Rozważmy przekształcenie ![]() określone wzorem
określone wzorem ![]() dla
dla ![]() ,
, ![]() .
Wówczas
.
Wówczas ![]() jest oczywiście mierzalne względem
jest oczywiście mierzalne względem ![]() -ciała zbiorów borelowskich na
-ciała zbiorów borelowskich na ![]() , ale nie istnieje borelowska miara niezmiennicza dla
, ale nie istnieje borelowska miara niezmiennicza dla ![]() .
Istotnie, ponieważ
.
Istotnie, ponieważ ![]() , mamy
, mamy ![]() , czyli
, czyli
![]() i, podobnie, sprawdzamy że
i, podobnie, sprawdzamy że ![]() . Zatem jedyna miara niezmiennicza musiałaby być skupiona w punkcie
. Zatem jedyna miara niezmiennicza musiałaby być skupiona w punkcie ![]() , ale, ponieważ
, ale, ponieważ ![]() , ta miara też nie jest niezmiennicza
, ta miara też nie jest niezmiennicza
Widzimy, że powyższy przykład jest nieco sztuczny; ciągłe przekształcenie zostało zmodyfikowane w punkcie stałym i w ten sposób wyrugowaliśmy jedyną miarę niezmienniczą dla wyjściowego, ciągłego przekształcenia domkniętego odcinka ![]() .
.
Istotnie mamy następujące
Twierdzenie 10.1 (Twierdzenie Kryłowa- Bogoliubowa)
Jeśli ![]() jest przestrzenią metryczną zwartą,
jest przestrzenią metryczną zwartą, ![]() przekształceniem ciągłym, to
istnieje przynajmniej jedna borelowska miara niezmiennicza dla
przekształceniem ciągłym, to
istnieje przynajmniej jedna borelowska miara niezmiennicza dla ![]() .
.
Uwaga 10.1
Zauważmy że to twierdzenie jest nietrywialne, o ile ![]() nie ma żadnej orbity okresowej.
Jeśli bowiem
nie ma żadnej orbity okresowej.
Jeśli bowiem ![]() jest orbitą okresową, to miara
jest orbitą okresową, to miara
jest niezmienniczą miarą borelowską.
Zanim przystąpimy do dowodu Twierdzenia, zapiszemy warunek na niezmienniczość miary w innej, równoważnej formie:
Przypomnijmy, że niezmienniczość miary oznacza że ![]() dla każdego mierzalnego zbioru
dla każdego mierzalnego zbioru ![]() .
Z przekształceniem ciągłym
.
Z przekształceniem ciągłym ![]() możemy związać ciągłe przekształcenie
możemy związać ciągłe przekształcenie ![]() dane wzprem
dane wzprem
Stwierdzenie 10.1
Jeśli ![]() jest przestrzenią metryczną zwartą,
jest przestrzenią metryczną zwartą, ![]() przekształceniem ciągłym to borelowska miara regularna jest niezmiennicza dla
przekształceniem ciągłym to borelowska miara regularna jest niezmiennicza dla ![]() wtedy i tylko wtedy gdy
wtedy i tylko wtedy gdy ![]() .
.
Założmy że ![]() . Mamy pokazać że dla każdego borelowskiego zbioru
. Mamy pokazać że dla każdego borelowskiego zbioru ![]() mamy
mamy ![]() .
Z regularności miary wynika że dla każdego dodatniego
.
Z regularności miary wynika że dla każdego dodatniego ![]() istnieją zbiory
istnieją zbiory ![]() (
(![]() - otwarty,
- otwarty, ![]() - domknięty) takie że
- domknięty) takie że
![]() oraz
oraz ![]() Istnieje funkcja ciągła
Istnieje funkcja ciągła ![]() taka że
taka że ![]() ,
, ![]() ,
, ![]() . Mamy zatem
. Mamy zatem
,
Stąd (skoro ![]() )
)
Wobec dowolności ![]() ,
, ![]() .
Odwrotnie, jeśli dla każdego
.
Odwrotnie, jeśli dla każdego ![]() borelowskiego
borelowskiego ![]() , to możemy napisać dla funkcji ciągłej
, to możemy napisać dla funkcji ciągłej ![]() , (ale także dla dowolnej borelowskiej,
, (ale także dla dowolnej borelowskiej,![]()
Z tego zapisu widać od razu że ![]() .
Ponieważ dowolną funkcję ciągłą
.
Ponieważ dowolną funkcję ciągłą ![]() możemy teraz zapisać jako różnicę dwóch funkcji ciągłych nieujemnych
możemy teraz zapisać jako różnicę dwóch funkcji ciągłych nieujemnych ![]() , dowód jest zakończony.
, dowód jest zakończony.
Dowód Twierdzenia Kryłowa- Bogoliubowa
Przypomnijmy że każda borelowska regularna miara na ![]() jest ciągłym funkcjonałem liniowym działającym na przestrzeni funkcji ciągłych
jest ciągłym funkcjonałem liniowym działającym na przestrzeni funkcji ciągłych ![]() i, odwrotnie, każdy nieujemny (tj przyjmujący nieujemne wartości na funkcjach nieujemnych) funkcjonał ciągły na
i, odwrotnie, każdy nieujemny (tj przyjmujący nieujemne wartości na funkcjach nieujemnych) funkcjonał ciągły na ![]() jest dany przez pewną miarę borelowską regularną.
(Ta odpowiedniość jest dana przez formułę: uscislic
jest dany przez pewną miarę borelowską regularną.
(Ta odpowiedniość jest dana przez formułę: uscislic
W przestrzeni miar probabilistycznych rozpatrujemy słabą![]() topologię (to znaczy topologię pochodzącą z utożsamienia miar z funkcjonałami liniowymi na
topologię (to znaczy topologię pochodzącą z utożsamienia miar z funkcjonałami liniowymi na ![]() , czyli elementami
, czyli elementami ![]() . Zastosujemy znane twierdzenie Banacha- Alaoglu, mówiące że kula jednostkowa w przestrzeni sprzężonej do przestrzeni Banacha jest zwarta w słabej
. Zastosujemy znane twierdzenie Banacha- Alaoglu, mówiące że kula jednostkowa w przestrzeni sprzężonej do przestrzeni Banacha jest zwarta w słabej![]() topologii.
topologii.
Uwaga 10.2
Słaba ![]() topologia w przestrzeni miar unormowanych jest metryzowalna
uzupelnic
topologia w przestrzeni miar unormowanych jest metryzowalna
uzupelnic
Wyberzmy dowolny punkt ![]() i rozpatrzmy ciąg miar
i rozpatrzmy ciąg miar
wybierzmy podciąg słabo zbieżny:
| (10.1) |
Miara ![]() jest wówczas szukaną miarą niezmienniczą.
jest wówczas szukaną miarą niezmienniczą.
Istotnie, sprawdzimy że ![]() .
Mamy
.
Mamy
| (10.2) |
Pozostaje jeszcze zauważyć że ![]() ,zaś
,zaś ![]() .
.
Przykład 10.2
Obrót o kąt niewymierny (dokładniej: niewspółmierny z ![]() ) na okręgu ma tylko jedną miarę niezmienniczą (jest nią oczywiście miara Lebesgue'a) - por. Stwierdzenie 2.1. Przekształcenia które mają tylko jedną miarę niezmienniczą nazywa się ścisle ergodycznymi.
) na okręgu ma tylko jedną miarę niezmienniczą (jest nią oczywiście miara Lebesgue'a) - por. Stwierdzenie 2.1. Przekształcenia które mają tylko jedną miarę niezmienniczą nazywa się ścisle ergodycznymi.
Ćwiczenie 10.1
uogólnienie na przesunięcia na torusach
Ćwiczenie 10.2 (Inna konstrukcja półsprzężenia homeomorfizmu okręgu z obrotem)
Niech ![]() będzie zachowującym orientację homeomorfizmem okręgu, o niewymiernej liczbie obrotu.
Niech
będzie zachowującym orientację homeomorfizmem okręgu, o niewymiernej liczbie obrotu.
Niech ![]() będzie borelowską miarą niezmienniczą. Wykazać że miara
będzie borelowską miarą niezmienniczą. Wykazać że miara ![]() jest bezatomowa.
Ustalmy
jest bezatomowa.
Ustalmy ![]() i oznaczmy przez
i oznaczmy przez ![]() dodatnio zorientowany łuk między punktami
dodatnio zorientowany łuk między punktami ![]() .
Określamy przekształcenie
.
Określamy przekształcenie ![]() wzorem
wzorem
Niech ![]() . Wykazać że wówczas
. Wykazać że wówczas ![]() jest ”pólsprzężeniem
jest ”pólsprzężeniem ![]() z obrotem
z obrotem ![]() o kąt
o kąt ![]() , tj.
, tj.
Jaki jest związek ![]() z liczbą obrotu dla
z liczbą obrotu dla ![]() ?
?
10.2. O sposobach szukania miar niezmienniczych w klasie miary Lebesgue'a. Operator Perrona-Frobeniusa
Jeśli rozważane przez nas przekszgtałcenie jest określone na podzbiorze ![]() o dodatniej mierze Lebesgue'a, lub na rozmaitości gładkiej, to naturalne jest pytanie o zachowanie trajektorii punktów typowych w sensie miary Lebesgue'a. Twierdzenie ergodyczne daje taką odpowiedź, pod warunkiem że
istnieje miara niezmiennicza (najlepiej: ergodyczna) bezwzględnie ciągła względem miary Lebesgue'a.
o dodatniej mierze Lebesgue'a, lub na rozmaitości gładkiej, to naturalne jest pytanie o zachowanie trajektorii punktów typowych w sensie miary Lebesgue'a. Twierdzenie ergodyczne daje taką odpowiedź, pod warunkiem że
istnieje miara niezmiennicza (najlepiej: ergodyczna) bezwzględnie ciągła względem miary Lebesgue'a.
Przykład 10.3
Rozważmy kawałkami afiniczne przekształcenie odcinka ![]() . Mamy:
. Mamy: ![]() . Każdy z odcinkow
. Każdy z odcinkow ![]() jest przekształcany afinicznie na cały odcinek
jest przekształcany afinicznie na cały odcinek ![]() .
.
Dla tego przekształcenia miara Lebesgue'a jest niezmiennicza (dlaczego?)
Jeśli teraz rozważymy podobne przekształcenie - ale dopuścimy żeby T przekształcalo ścisle monotonicznie i gładko każdy z odcinków naszego podziału na cały odcinek ![]() ale niekoniecznie afinicznie - to miara Lebesgue'a (na ogól) nie jest już niezmiennicza.
NA tym prostym przykładzie omówimy technikę, która pozwala (również w znacznie ogólniejszych sytuacjach) rozstrzygać o istnieniu miary niezmienniczej w klasie miary Lebesgue'a i o jej własnościach.
Wykres przekształcenia
ale niekoniecznie afinicznie - to miara Lebesgue'a (na ogól) nie jest już niezmiennicza.
NA tym prostym przykładzie omówimy technikę, która pozwala (również w znacznie ogólniejszych sytuacjach) rozstrzygać o istnieniu miary niezmienniczej w klasie miary Lebesgue'a i o jej własnościach.
Wykres przekształcenia ![]() jest przedstawiony na rysunku 10.1.
jest przedstawiony na rysunku 10.1.
Twierdzenie 10.2
Niech ![]() . Oznaczmy
. Oznaczmy ![]() (zatem
(zatem ![]() ).
).
Rozpatrujemy przekształcenie ![]() o następujących własnościach:
o następujących własnościach:
-
(1)
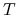 jesli klasy
jesli klasy 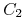 na każdym odcinku
na każdym odcinku 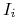 i przekształca ścisle monotonicznie odcinek
i przekształca ścisle monotonicznie odcinek 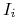 na
na 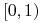 .
. -
(2)
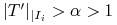
-
(3)
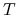 rozszerza się do przekształcenia klasy
rozszerza się do przekształcenia klasy 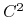 na trochę większy odcinek (zatem druga pochodna
na trochę większy odcinek (zatem druga pochodna 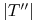 jest ograniczona na
jest ograniczona na 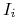 )
)
Wówczas istnieje miara niezmiennicza bezwzględnie ciągła względem miary Lebesgue'a. Ponadto, gęstość ![]() tej miary względem miary Lebesgue'a jest ograniczona z gory i z dołu: istnieją stałe
tej miary względem miary Lebesgue'a jest ograniczona z gory i z dołu: istnieją stałe ![]() takie że
takie że
Będziemy postępować według dowodu twierdzenia Kryłowa- Bogoliobowa, biorąc za punkt startowy- miarę Lebesgue'a na odcinku ![]() .
Oznaczmy ją przez
.
Oznaczmy ją przez ![]() . Rozpatrujemy ciąg miar
. Rozpatrujemy ciąg miar ![]() . Następnie rozpatrzymy (tak jak w dowodzie tw Kryłowa- Bogoliubowa)
średnie miar
. Następnie rozpatrzymy (tak jak w dowodzie tw Kryłowa- Bogoliubowa)
średnie miar ![]()
Nie jest trudno zauważyć że każda z tych miar jest bezwzględnie ciągła względem miary Lebesgue'a. Ale oczywiście nie wynika stąd że słaba granica podciągu jest też absolutnie ciągła. Dlatego udowodnimy trzy pomocnicze stwierdzenia. Najpierw wprowadzimy oznaczenie
Zauważmy że odcinek ![]() jest podzielony na rozłaczne
jest podzielony na rozłaczne ![]() i że każdy odcinek
i że każdy odcinek ![]() jest przekształcany przez iterację
jest przekształcany przez iterację ![]() ściśle monotonicznie na
ściśle monotonicznie na ![]() .
.
Stwierdzenie 10.2
Miara ![]() jest bezwzględnie ciągła względem miary Lebesgue'a z gęstością
jest bezwzględnie ciągła względem miary Lebesgue'a z gęstością
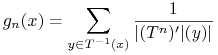 |
(10.3) |
Funkcja ![]() jest klasy
jest klasy ![]()
Wzór na gęstość obrazu miary Lebesgue'a przy przekstałceniu ![]() wynika bezpośrednio z wzoru na całkowanie przez podstawienie. Zostawiamy jako ćwiczenie.
wynika bezpośrednio z wzoru na całkowanie przez podstawienie. Zostawiamy jako ćwiczenie.
Stwierdzenie 10.3
Ciąg funkcji ![]() jest wspólnie ograniczony z góry i z dołu: istnieją stałe
jest wspólnie ograniczony z góry i z dołu: istnieją stałe ![]() takie że
takie że
Weźmy dwa punkty ![]() . Wówczas każdy z tych punktów na
. Wówczas każdy z tych punktów na ![]() przeciwobrazów przy
przeciwobrazów przy ![]() ; każdy w innym odcinku
; każdy w innym odcinku ![]() .
Możemy je więc w naturalny sposób polączyc w pary. Zatem dwa przeciwobrazy
.
Możemy je więc w naturalny sposób polączyc w pary. Zatem dwa przeciwobrazy ![]() są w parze jeśli dla każdego
są w parze jeśli dla każdego ![]() punkty
punkty
![]() i
i ![]() należą do tego samego przedziału monotoniczności
należą do tego samego przedziału monotoniczności ![]() . POnieważ na każdym takim przedziale
. POnieważ na każdym takim przedziale ![]() jest ograniczona,
jest ograniczona, ![]() , więc funkcjia
, więc funkcjia ![]() spełnia warunek Lipschitza. Oznaczmy przez
spełnia warunek Lipschitza. Oznaczmy przez ![]() wspólną stałą Lipschitza (dla wszystkich przedziałów). Możemy teraz porównać
wspólną stałą Lipschitza (dla wszystkich przedziałów). Możemy teraz porównać ![]() i
i ![]() :
Mamy
:
Mamy
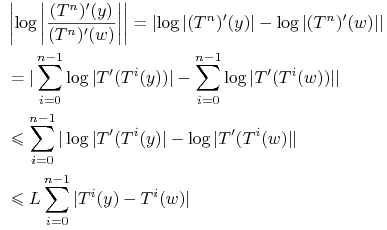 |
(10.4) |
Ponieważ przekształcenie ![]() jest kawałkami rozszerzające (
jest kawałkami rozszerzające (![]() ) , więc
) , więc ![]() . Ostatnie wyrażenie można więc oszacować z góry przez uniwersalną stałą, niezależną od
. Ostatnie wyrażenie można więc oszacować z góry przez uniwersalną stałą, niezależną od ![]() (sumę odpowiedniego szeregu geometrycznego). Stąd wynika że
(sumę odpowiedniego szeregu geometrycznego). Stąd wynika że
dla pewniej stałej ![]() .
Z wzoru (10.3) natychmiast wynika teraz że
.
Z wzoru (10.3) natychmiast wynika teraz że
Ponieważ ![]() jest gęstością miary
jest gęstością miary ![]() , więc
, więc ![]() . Istnieje zatem punkt
. Istnieje zatem punkt ![]() taki że
taki że ![]() . Stąd zaś wynika że dla każdego
. Stąd zaś wynika że dla każdego ![]() mamy
mamy ![]() . Z tego samego powodu:
. Z tego samego powodu: ![]() dla każdego
dla każdego ![]() .
.
Ostatnie stwierdzenie jest ogólne; nie dotyczy tylko tej konkretnej sytuacji:
Stwierdzenie 10.4
Jeśli ciąg miar probabilistycznych ![]() na prostej jest słabo-
na prostej jest słabo-![]() zbieżny do miary
zbieżny do miary ![]() i gęstości miar
i gęstości miar ![]() są wspólnie ograniczone z gory i z dołu przez stałe dodatnie
są wspólnie ograniczone z gory i z dołu przez stałe dodatnie ![]() , to miara graniczna
, to miara graniczna ![]() też jest bezwzględnie ciągła i gęstość jest ograniczona przez te same stałe (prawie wszędzie).
też jest bezwzględnie ciągła i gęstość jest ograniczona przez te same stałe (prawie wszędzie).
Skorzystamy z równoważnej charakteryzacji słabej zbieżności miar (rozkładów) na prostej: ciąg miar jest słabo zbieżny wtedy i tylko wtedy gdy ciąg dystrybuant jest zbieżny punktowo, w każdym punkcie ciągłości dystrybuanty miary granicznej.
Zatem- jesli ![]() i rozpatrzymy odcinek
i rozpatrzymy odcinek ![]() taki że
taki że ![]() (czyli
(czyli ![]() nie ma atomów w końcach przedziału) to
nie ma atomów w końcach przedziału) to
Zatem- dla każdego odcinka ![]() którego końce nie są atomami miary
którego końce nie są atomami miary ![]()
| (10.5) |
Atomów jest tylko przeliczalnie wiele, więc każdy odcinek ![]() można przybliżyć z góry odcinkami o końcach nie będących atomami. Łatwo stąd widać że nierówność (10.5) zachodzi dla wszystkich przedziałów
można przybliżyć z góry odcinkami o końcach nie będących atomami. Łatwo stąd widać że nierówność (10.5) zachodzi dla wszystkich przedziałów ![]() .
Ponieważ dla każdego zbioru borelowskiego w
.
Ponieważ dla każdego zbioru borelowskiego w ![]() można znaleźć zawierający go zbiór otwarty (czyli sumę przeliczanej liczby otwartych odcinków) o mierze Lebesgue'a dowolnie blisko przybliżającej miarę naszego zbioru, łatwo stąd otrzymujemy nierówność (10.5) dla dowolnego zbioru borelowskiego.
Wynika stąd że miara
można znaleźć zawierający go zbiór otwarty (czyli sumę przeliczanej liczby otwartych odcinków) o mierze Lebesgue'a dowolnie blisko przybliżającej miarę naszego zbioru, łatwo stąd otrzymujemy nierówność (10.5) dla dowolnego zbioru borelowskiego.
Wynika stąd że miara ![]() jest bezwzględnie ciągła względem miary Lebesgue'a i że gęstość jest ograniczona z góry przez
jest bezwzględnie ciągła względem miary Lebesgue'a i że gęstość jest ograniczona z góry przez ![]() .
Podobnie otrzymujemy teraz ograniczenie z dołu gęstości przez
.
Podobnie otrzymujemy teraz ograniczenie z dołu gęstości przez ![]() .
Szczegóły pomijamy.
.
Szczegóły pomijamy.
Z tych trzech stwierdzeń teza naszego Twierdzenia wynika natychmiast; wystarczy zauważyć że ograniczenia na gęstość miar ![]() z góry i z dołu przenoszą się od razu na takie same ograniczenia dla gęstości miar
z góry i z dołu przenoszą się od razu na takie same ograniczenia dla gęstości miar ![]() . Szukana miara niezmiennicza jest słabą granicą pewnego podciągu ciągu miar
. Szukana miara niezmiennicza jest słabą granicą pewnego podciągu ciągu miar ![]() .
.
Wykażemy jeszcze
Twierdzenie 10.3
Miara ![]() jest ergodyczna.
jest ergodyczna.
Szkic dowodu
Do dowodu ergodyczności posłużymy się twierdzeniem Lebesgue'a o punktoach gęstości. Założmy zatem że miara ![]() nie jest ergodyczna;
istnieje wówczas w pełni niezmienniczy podzbiór
nie jest ergodyczna;
istnieje wówczas w pełni niezmienniczy podzbiór ![]() miary niezerowej i niepełnej Wówczas również
miary niezerowej i niepełnej Wówczas również ![]() i
i ![]() .
Z twierdzenia Lebesgue'a wynika że prawie każdy punkt
.
Z twierdzenia Lebesgue'a wynika że prawie każdy punkt ![]() jest punktem gęstości tego zbioru.
jest punktem gęstości tego zbioru.
Niech ![]() będzie odcinkiem
będzie odcinkiem ![]() - tego podziału do którego należy
- tego podziału do którego należy ![]() . Z szacowania (10.4) zastosowanego do dowlonych punktów
. Z szacowania (10.4) zastosowanego do dowlonych punktów ![]() wynika że wahanie pochodnej
wynika że wahanie pochodnej ![]() na odcinkach
na odcinkach ![]() -tego podziału jest ograniczone przez stałą
-tego podziału jest ograniczone przez stałą ![]() .
Stąd i z niezmienniczości zbioru
.
Stąd i z niezmienniczości zbioru ![]() wnioskujemy że
wnioskujemy że
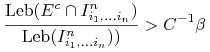 |
(10.6) |
Jeśli teraz ![]() jest kulą o środku w
jest kulą o środku w ![]() i promieniu równym długości odcinka
i promieniu równym długości odcinka ![]() , to otrzymujemy stąd
, to otrzymujemy stąd
| (10.7) |
co oczywiście przeczy temu że ![]() jest punktem gęstości.
jest punktem gęstości.





