Zagadnienia

12.1 Metryka hiperboliczna
12.2 Potok geodezyjny w $\mathbb{H}^{2}$

12. Potok geodezyjny na rozmaitości o stałej ujemniej krzywiźnie- ważny przykład potoku Anosowa

12.1. Metryka hiperboliczna

Wprowadzimy bardzo ważne wanalizie zespolonej pojęcie płaszczyzny hiperbolicznej

Definicja 12.1

Niech

$\mathbb{H}^{2}=\{(x,y)\in\mathbb{C}:{\rm im}(z)>0$

(czyli - gówna półpłaszczyzna) W $\mathbb{H}^{2}$ wprowadzamy metrykę (Riemannowską):

$|dz|\cdot\frac{1}{y}$

Inaczej mówiąc: w nowej metryce, długość $||v||_{h}$ wektora $v$ należącego do przestrzeni stycznej $T_{z}\mathbb{H}^{2}$ jest równa $\frac{1}{y}||v||_{e}$ (przez $||v||_{e}$ oznaczyliśmy normę euklidesową, a przez $||v||_{h}$ - hiperboliczną). Jeszcze inaczej: w metryce euklidesowej iloczyn skalarny wektorów $v,w$ stycznych w punkcie $z=x+iy$ jest równy $<v,w>_{e}=u\overline{w}$ . Iloczyn skalarny w nowej metryce jest równy

$<v,w>_{h}=u\overline{w}\cdot\frac{1}{y^{2}}.$

Ćwiczenie 12.1

Sprawdzić że wszystkie homografie (przekształcenia Möbiusa) zachowujące $\mathbb{H}^{2}$ są postaci:

$T(z)=\frac{az+b}{cz+d},$

$\left(\begin{array}[]{rrrr}a&b\\ c&d\\ \end{array}\right)\in GL_{+}(2,\mathbb{R})$

Stwierdzenie 12.1

Wszystkie homografie zachowujące $\mathbb{H}^{2}$ są izometriami w metryce hiperbolicznej w $\mathbb{H}^{2}$ .

Każde takie przekształcenie można zapisać jako złożenie trzech, postaci $z\to z+A$ , $z\to Bz$ , $z\to-\frac{1}{z}$ , $A,B>0$ . Wystarczy sprawdzić że te trzy przekształcenia są izometriami. Sprawdzimy trzecie: mamy

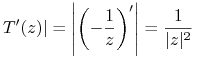$T^{{\prime}}(z)|=\left|\left(-\frac{1}{z}\right)^{{\prime}}\right|=\frac{1}{|z|^{2}}$

Należy sprawdzić że

$|T^{{\prime}}(z)|\cdot\frac{1}{{\rm im}T(z)}\cdot{\rm im}z=1$

Równość zachodzi, ponieważ ${\rm im}T(z)=\frac{y}{|z|^{2}}$ , ${\rm im}z=y$

∎

Ćwiczenie 12.2

Niech $z\in\mathbb{H}^{2}$ , $v\in T_{z}\mathbb{H}^{2}$ , $z^{{\prime}}\in\mathbb{H}^{2}$ , $v^{{\prime}}\in T_{z}\mathbb{H}^{2}$ . Wówczas istnieje izometria $T:\mathbb{H}^{2}\to\mathbb{H}^{2}$ taka że $T(z)=z^{{\prime}}$ , $DT_{z}(v)=v^{{\prime}}$ .

Stwierdzenie 12.2

Geodezyjne w $\mathbb{H}^{2}$ są to łuki (pół)okręgów prostopadłych do prostej $y=0$ . Geodezyjną jest też okrąg przechodzący przez punkt w nieskończoności, czyli - każda (pół)prosta prostopadła do prostej $y=0$ .

Definicja 12.2

Wprowadzamy metrykę w $S\mathbb{H}^{2}$ (czyli w wiązce wektorów stycznych o długości hiperbolicznej $1$ ). tu rysunek

Niech $x=(p,v),y=(q,w)$ . Jeśli $p=q$ to miarą odległości między $x$ , $y$ jest $d(v,w)$ - miara kąta między wektorami $w$ , $v$ . Jeśli $p\neq q$ to istnieje dokładnie jedna geodezyjna $\gamma$ przechodząca przez punkty $p$ , $q$ . Niech $w^{{\prime}}\in T_{p}\mathbb{H}^{2}$ będzie obrazem $w$ przy przesunięciu równoległym wzdłuż tej geodezyjnej. Inaczej- mozna powiedziec tak: Rozpatrujemy izometrie (przekształcenia Möbiusa) dla których geodezyjna $\gamma$ jest niezmiennicza (jak je znaleźć?) i wybieramy przekształcenie $T$ - taką spośród tych izometrii, która punkt $q$ przekształca na $p$ . Wektor $w^{{\prime}}$ jest równy $DT_{q}(w)$ .

Odległość między $x$ , $y$ definiujemy:

$d(x,y)=\sqrt{d(v,w^{{\prime}})^{2}+d_{h}(p,q)^{2}}$

12.2. Potok geodezyjny w 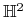$\mathbb{H}^{2}$

Niech $x=(p,v)\in S\mathbb{H}^{2}$ Potok geodezyjny $\varphi^{t}(x)$ można, jak wiemy opisac następujaco: znajdujemy jedyną geodezyjną $\gamma(t)$ taką że $\gamma(0)=p$ , $\dot{\gamma}(0)=v$ . Po czasie $t$ mamy $\varphi^{t}(x)=(y,w)$ gdzie $y=\gamma(t)$ , $w=\dot{\gamma}(t)$ . tu rysunek

Rozpatrzmy zatem $x=(i,v=(0,1))$ . Geodezyjna zawierająca punkt $i$ , wypuszczona w kierunku $v$ to oczywiście półprosta pionowa $\gamma(t)=(0,e^{t})=i\cdot e^{t},t\in\mathbb{R}$ . Użyliśmy parametryzacji $e^{t}$ ponieważ ma to być parametryzacja odpowiadająca ruchowi ze stała prędkościa: $||\dot{\gamma}(t)||_{h}=1$ . Mamy:

$||\dot{\gamma}(t)||_{h}=|\dot{\gamma}(t)|\cdot\frac{1}{{\rm im}\gamma(t)}=\frac{e^{t}}{e^{t}}=1$

Zatem: $\varphi^{t}(x)=(e^{t}i,v_{t})$ , gdzie wektor $v_{t}$ jest to wektor $(0,1)$ zaczepiony w punkcie $e^{t}i$

NIech teraz $y=((a+i),w)\in S\mathbb{H}^{2}$ , $a\in\mathbb{R}$ . Oczywiście mamy $\varphi^{t}(y)=(e^{t}(a+i),w_{t})$ gdzie wektor $w_{t}$ jest to wektor $(0,1)$ zaczepiony w punkcie $e^{t}(a+i)$

Zobaczmy jak zmienia się z czasem odległość:

$d(\varphi^{t}(x),\varphi^{t}(y)$

. Mamy:

$d_{h}\left(e^{t}i,e^{t}(a+i)\right)\asymp e^{{-t}}$

(dlaczego?)

Podobnie

$d(\varphi^{t}(x),\varphi^{t}(y)\asymp e^{{-t}}.$

Ta obserwacja prowadzi do definicji:

Definicja 12.3

Horocykl to każda linia pozioma $\mathbb{R}+ir$ i każdy obraz tej linii przy przekształceniu Möbiusa zachowującym $\mathbb{H}^{2}$ .

tu rysunek Widzimy że dla każdego $x=(p,v)\in S\mathbb{H}^{2}$ istnieje dokładnie jedna geodezyjna wyznaczona przez ten punkt i wektor i dokładnie dwa horocykle takie że punkt $p$ należy do horocyklu, zaś wektor $v$ jest normalny do horocyklu. Nazwijmy je odpowiednio horocyklem wchodzącym i horocyklem wychodzącym wyznaczonymi przez $x=(p,v)$

tu dwa rysunki: geodezyjna, horocykl wchodzący i wychodzący- dla geodezyjnej pionowej i dla geodezyjnej ”typowej”

Niech $x=(p,v)$ . Rozpatrzmy horocykl wchodzący wyznaczony przez $x$ , W każdym punkcie horocyklu wybieramy wektor normalny do horocyklu , w ten sposób aby wybór był ciągły i aby wektor $v$ był wybrany. Otrzymujemy jednowymiarową podrozmaitość $S\mathbb{H}^{2}$ . Oznaczmy ją przez $W^{{ss}}((p,v)$ . Podobnie, rozważmy horocykl wychodzący wyznaczony przez $x$ i wybierzmy ciągłą rodzine wektorów normalnych do niego, tak aby wektor $v$ należał do tej rodziny. Tę podrozmaitość oznaczamy $W^{{uu}}((p,v)$ .

Wyliczenie(powyżej) zmiany odległości przy $\varphi^{t}$ dla punktów (i odpowiednich wektorów) zachowuje się przy zastosowaniu izometrii; powyższy racunek prowadzi do Stwierdzenia (szczegóły pomijamy)

Stwierdzenie 12.3

Zbiór $W^{{ss}}((p,v)$ stanowi silną rozmaitość stabilną punktu $x=(p,v)$ ; dla każdego $y\in W^{{ss}}((p,v)$ $d(\varphi^{t}(y),\varphi^{t}(x)\to 0$ gdy $t\to\infty$ .

Zbiór $W^{{uu}}((p,v)$ jest silną rozmaitością niestabilną punktu $x=(p,v)$ ; dla każdego $y\in W^{{uu}}((p,v)$ $d(\varphi^{t}(y),\varphi^{t}(x)\to 0$ gdy $t\to-\infty$ .

Ćwiczenie 12.3

Uzupełnić brakujące szczególy; w szczególności wykazać że wskazany zbiór wyczerpuje cała rozmaitość stabilną (niestabilną); tzn jeżeli $y\notin W^{{ss}}((p,v)$ , to $d(\varphi^{t}(y),\varphi^{t}(x)\nrightarrow 0$

Oprócz silnej rozmaitości (nie)stabilnej mamy jeszcze słabą rozmaitość (nie)stabilną. Zauważmy że jeśli $(p^{{\prime}}v^{{\prime}})$ jest punktem (w $S\mathbb{H}^{2}$ należącym do geodezyjnej wyznaczonej przez $(p,v)$ , to $(p^{{\prime}},v^{{\prime}})=\varphi^{s}(p,v)$ dla pewnego $s$ , zatem $d((p,v),(p^{{\prime}}v^{{\prime}})=d(\varphi^{t}(p,v),\varphi^{t}(p^{{\prime}},v^{{\prime}})$ dla wszystkich $t\in\mathbb{R}$ . Mamy więc

Stwierdzenie 12.4

Słaba rozmaitość stabilna $W^{s}(x)$ punktu $x=(p,v)$ jest sumą wszystkich silnych rozmaitości stabilnych punktów $x^{{\prime}}=(p^{{\prime}},v^{{\prime}})$ należących do geodezyjnej wyznaczonej przez $x=(p,v)$ .

$W^{s}(x)=\{ y\in S\mathbb{H}^{2}:\sup _{{t\ge 0}}d(\varphi^{t}(x),\varphi^{t}(y))<\infty.$

Oczywiscie- symetryczne stwierdzenie mamy dla rozmaitości niestabilnej. Silne rozmaitości są jednowymiarowe, słabe - są dwuwymiarowe.

Przecięciem słabej rozmaitości stabilnej i niestabilnej przechodzącej przez $(p,v)$ jest geodezyjna wyznaczona przez $(p,v)$ , a precyzyjniej- jej podniesienie do $S\mathbb{H}^{2}$ .

Wniosek 12.1

Otrzymalismy w ten sposób globalną foliację stabilna i niestabilną dla potoku geodezyjnego na $S\mathbb{H}^{2}$ .

Każdą zwartą orientowalną powierzchnię $M$ można (topologicznie) utożsamiać z przestrzenią ilorazową $\mathbb{H}^{2}/\Gamma$ dla pewnej dyskretnej podgrupy grupy zachowujących orientację izometrii $\mathbb{H}^{2}$ ( $\Gamma$ jest wówczas grupą podstawową tej powierzchni). Na rysunku (rysunek: osmiokąt hiperboliczny i dwuprecel i utożsamienia) przedstawiona jest realizacja ”dwuprecla” (czyli sfery z dwiema rączkami) jako hiperbolicznego ośmiokąta $O$ z odpowiednimi sklejeniami. Po dokonaniu wskazanych utożsamień boków ośmiokąta otrzymujemy (topologicznie) dwuprecel. W szczególności wszystkie wierzchołki ośmiokąta sklejają się w jeden punkt. wszystkie kąty tego ośmiokąta są równe $\frac{\pi}{4}$ . (zatem suma jest równa $2\pi$ .

Rozpatrzmy izometrie odpowiadające tym utożsamieniom: bok $a$ jest utożsamiany z $a^{{\prime}}$ (i odpowiednio pozostałe kroki) przy pomocy hiperbolicznej homografii (przesunięcia wzdłuz geodezyjnej). Grupa $\Gamma$ generowana przez te homografie jest dyskretną podgrupą pełnej grupy izometrii. Działając elementami tej grupy na ośmiokąt $O$ otrzymujemy ”parkietaż” dysku Poincare'go $D$ . Ośmiokąt $O$ (i każda z jego kopii jest dziedziną fundamentalną dla działania grupy $\Gamma$ .

Ćwiczenie 12.4

Jakie znaczenie mają w tej konstrukcji miary kątów ośmiokąta $O$ ?

Zatem powierzchnia $M$ jest homeomorficzna z przestrzenią ilorazową $\mathbb{D}/\Gamma$ . Ponieważ grupa $\Gamma$ działa przez izometrie, metryka hiperboliczna rzutuje się na metrykę riemannowską na $M$ ; mazywamy ją też metryką hiperboliczną.

Uwaga 12.1

Na jednej powierzchni istnieje wiele, nieizometrycznych metryk hiperbolicznych.

Ponieważ rzutowanie jest lokalną izometrią, obrazami ( przeciwobrazami) geodezyjnych przy rzutowaniu są geodezyjne. Potok geodezyjny na rozmaitości $M=\mathbb{D}/\Gamma$ jest więc obrazem potoku na $\mathbb{D}$ , czyli (izometrzycznie) na $\mathbb{H}^{2}$ .

Wykorzystując wykazane wcześniej istnienie globalnej foliacji stabilnej i niestabilnej dla potoku geodezyjnego i powyższą uwagę otrzymujemy

Twierdzenie 12.1

Niech $M$ bedzie zwartą rozmaitością otrzymaną jako przestrzeń ilorazowa $\mathbb{D}/\Gamma$ (gdzie $\Gamma$ jest dyskretną podgrupą grupy zachowujących orientację izometrii $\mathbb{D}$ , z dziedziczoną z $\mathbb{D}$ metryką hiperboliczną. Wówczas potok geodezyjny na $SM$ jest potokiem Anosowa.

Wykażemy jeszcze

Twierdzenie 12.2

Jeśli $\Gamma$ jest dyskretną podgrupą izometrii $\mathbb{D}$ zachowujących orientację, taką że $M=\mathbb{D}/\Gamma$ jest zwarta, to orbity okresowe (czyli podniesienia zamkniętych geodezyjnych) są gęste w $SM$ .

Wybierzmy punkt $(x,v)\in SM$ i wyznaczoną przez $(x,v)$ geodezyjną $C(t)$ . Zatem $C(0)=x,\dot{C}(0)=v$ . Wówczas krzywa $c(t)$ - przeciwobraz $C$ przy rzutowaniu $\pi$ jest geodezyjną w $\mathbb{D}$ ; niech $c(0)\in O$ . Niech $z_{1},z_{2}\in\mathbb{S}^{1}$ będą końcami tej geodezyjnej (rysunek); rozważmy otoczenia $U$ i $V$ tych punktów otrzymane przez łuki geodezyjnych, prostopadłych do $c$ . Geodezyjną $c$ możemy pokryć kopiami dziedziny fundamentalnej $O$ (czyli obrazami $O$ przy działąniu elementami grupy $\Gamma$ ). Ponieważ wszystkie takie kopie $O_{i}$ mają tę samą średnicę hiperboliczną; te kopie które są blisko brzegu $\mathbb{D}$ , mają małą średnicę euklidesową. Można więc znaleźć jakies $O_{i}\subset U$ i $O_{j}\subset$ . Mamy więc wyróżnione trzy obszary z naszego parkietażu, przecinające geodezyjną $c$ : $O_{i}$ , $O$ , $O_{j}$ , położone w tej kolejności ”wzdłuż” geodezyjnej $c$ . Niech $\gamma\in\Gamma$ będzie taką izometrią należącą do $\Gamma$ , że $\gamma(O_{i})=O_{j}$ . Wówczas $\gamma$ jest izometrią hiperboliczną; jeden jej punkt stały jest w $U$ , drugi w $V$ . Niech $\tilde{c}$ będzie ”osią” tej izometrii. Wówczas $\tilde{c}$ rzutuje się na zamkniętą geodezyjną na $M$ . Ponieważ otoczenia $U,V$ mogą być dowolnie małe, można w ten sposób znaleźć punkt $(\tilde{x},\tilde{v})\in\tilde{c}$ blisko $(x,v)$ . Punkt $(\tilde{x},\tilde{v})$ pod działaniem potoku geodezyjnego ma okresową trajektorię.

∎