Zagadnienia
13. Zbiory hiperboliczne i ergodyczność
13.1. Geometryczny dowód ergodyczności dla prostego układu hiperbolicznego
Twierdzenie 13.1
Niech ![]() będzie hiperbolicznym automorfizmem torusa
będzie hiperbolicznym automorfizmem torusa ![]() . Jak wiemy,
. Jak wiemy, ![]() zachowuje miarę Lebesgue'a. Posługując się stukturą hiperboliczną (cały torus jest dla tego układu zbiorem hiperbolicznym) wykażemy że miara Lebesgue'a jest ergodyczna.
zachowuje miarę Lebesgue'a. Posługując się stukturą hiperboliczną (cały torus jest dla tego układu zbiorem hiperbolicznym) wykażemy że miara Lebesgue'a jest ergodyczna.
Niech ![]() będzie funkcją próbną; na początek zakłądamy że
będzie funkcją próbną; na początek zakłądamy że ![]() jest ciągła.
jest ciągła.
Rozpatrzmy funkcje
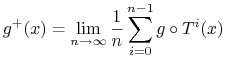 |
oraz
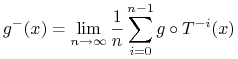 |
Z twierdzenia Birkhoffa wynika że
ma pełną miarę.
Ponieważ ![]() jest hiperboliczne, mamy niezmiennicze globalne foliacje stabilną i niestabilną.
Ustalmy
jest hiperboliczne, mamy niezmiennicze globalne foliacje stabilną i niestabilną.
Ustalmy ![]() i kawałek rozmaitości stabilnej
i kawałek rozmaitości stabilnej ![]() , a następnie- zbiór
, a następnie- zbiór
Dla małego ![]() ten zbiór jest równoległościanem.
ten zbiór jest równoległościanem.
Punkt początkowy ![]() musimy wybrać tak, żeby
musimy wybrać tak, żeby
![]() było podzbiorem pełnej miary w
było podzbiorem pełnej miary w ![]() . Istnienie wielu takich
. Istnienie wielu takich ![]() wynika z tw Fubiniego.
wynika z tw Fubiniego.
Wówczas zbiór
jest pełnej miary w ![]() .
.
Weźmy ![]() . Istnieją więc
. Istnieją więc ![]() oraz
oraz ![]() .
Mamy wówczas
.
Mamy wówczas
-
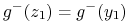 bo
bo 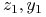 leżą w tym samym włóknie niestabilnym więc zbliżają się przy działaniu
leżą w tym samym włóknie niestabilnym więc zbliżają się przy działaniu
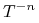 .
. -
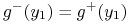
-
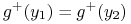 bo
bo 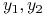 leżą w tym samym włóknie stabilnym.
leżą w tym samym włóknie stabilnym. -
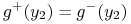
-
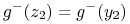 bo
bo 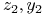 leżą w tym samym włóknie niestabilnym
leżą w tym samym włóknie niestabilnym
Ponieważ całą naszą rozmaitość możemy pokryć przez skończenie wiele takich ”prostokątów” ![]() , otrzymujemy
wniosek:
, otrzymujemy
wniosek: ![]() i
i ![]() są stałe prawie wszędzie, i równe
są stałe prawie wszędzie, i równe ![]() .
.
W następnym kroku dowodu pokażemy że to samo jest prawdą jeśli ![]() zastąpimy dowolną funkcją
zastąpimy dowolną funkcją ![]() .
Niech
.
Niech ![]() . Dla dowolnego
. Dla dowolnego ![]() istnieje funkcja
istnieje funkcja ![]() ciągła taka że
ciągła taka że ![]() .
.
Z twierdzenia ergodycznego wynika że prawie wszędzie istnieje, niekoniecznie stała granica
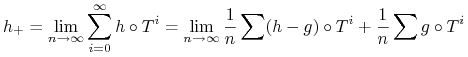 |
Wiemy już że druga granica jest równa stałej ![]() .
Orzymujemy stąd wniosek- funkcja graniczna
.
Orzymujemy stąd wniosek- funkcja graniczna ![]() nie może różnić się bardzo od stałej. Dokładniej- mamy:
nie może różnić się bardzo od stałej. Dokładniej- mamy:
Oznaczmy funkcję ![]() .
Z twierdzenia ergodycznego wynika że
.
Z twierdzenia ergodycznego wynika że ![]() prawie wszędzie i w
prawie wszędzie i w ![]() .
Zatem
.
Zatem
Normę ![]() można zaś oszacować:
można zaś oszacować:
Zatem
Wynika stąd więc że
Zatem ![]() różni się od stałej
różni się od stałej ![]() o mniej niż
o mniej niż ![]() . Wobec dowolności
. Wobec dowolności ![]() , dowodzi to że
, dowodzi to że ![]() jest stałe prawie wszędzie.
Dowód ergodyczności przekształcenia
jest stałe prawie wszędzie.
Dowód ergodyczności przekształcenia ![]() względem niezmienniczej miary Lebesgue'a jest więc zakończony.
względem niezmienniczej miary Lebesgue'a jest więc zakończony.
Uwaga 13.1
Ergodyczność tego konkretnego przekształcenia można wykazać również inaczej (zadanie). Na tym prostym przykładzie prześledziliśmy jednak dość ogólną metodę dowodzenia ergodyczności.
Uwaga 13.2
Widzimy że dowód nie wykorzystywał szczególnych własności przekształcenia ![]() ; wykorzystywał natomiast- strukturę hiperboliczną, czyli istnienie regularnych foliacji stabilnej i niestabilnej i zbudowanie z nich ”prostokątów”.
Ten ogólny schemat dowodzenia ergodyczności przy istniejącej strukturze hiperbolicznej pochodzi od Hopfa.
Poniżej sprawdzimy w tej sposób ergodyczność potoku geodezyjnego (oczywiście- nie kazdego!).
; wykorzystywał natomiast- strukturę hiperboliczną, czyli istnienie regularnych foliacji stabilnej i niestabilnej i zbudowanie z nich ”prostokątów”.
Ten ogólny schemat dowodzenia ergodyczności przy istniejącej strukturze hiperbolicznej pochodzi od Hopfa.
Poniżej sprawdzimy w tej sposób ergodyczność potoku geodezyjnego (oczywiście- nie kazdego!).
13.2. Potok geodezyjny na rozmaitości o stałej ujemnej krzywiźnie- ergodyczność
.
W wykładzie 11 wykazaliśmy że potok geodezyjny na wiązce sfer ![]() zachowuje naturalną gładką miarę- miarę
Liouville'a.
W wykładzie 12 wykazaliśmy że potok geodezyjny na powierzchni o stałej ujemniej krzywiźnie jest potokiem Anosowa.
Wykorzystamy teraz te fakty i, stosując argument Hopfa wykażemy ważne
zachowuje naturalną gładką miarę- miarę
Liouville'a.
W wykładzie 12 wykazaliśmy że potok geodezyjny na powierzchni o stałej ujemniej krzywiźnie jest potokiem Anosowa.
Wykorzystamy teraz te fakty i, stosując argument Hopfa wykażemy ważne
Twierdzenie 13.2
Niech ![]() będzie dyskretną grupą zachowujacych orientację izometrii
będzie dyskretną grupą zachowujacych orientację izometrii ![]() , działającą bez punktów stałych.
Załóżmy też że rozmaitość
, działającą bez punktów stałych.
Załóżmy też że rozmaitość ![]() jest zwarta. Wówczas potok geodezyjny na
jest zwarta. Wówczas potok geodezyjny na ![]() jest ergodyczny względem miary Liouville'a (oznaczmy ją
jest ergodyczny względem miary Liouville'a (oznaczmy ją ![]() ) na
) na ![]() .
.
Podobnie jak w przypadku opisanym w poprzednim rozdziale, wystarczy wykazać że jeśli ![]() jest funkcją ciągła w
jest funkcją ciągła w ![]() to
średnia ergodyczna
to
średnia ergodyczna
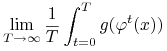 |
(13.1) |
jest stała prawie wszędzie.
Ponadto, wystarczy wykazać że dla istnieje pokrycie ![]() zbiorami otwartymi (tak jak poprzednio- prostokątami), na których ta granica jest stała prawie wszędzie.
zbiorami otwartymi (tak jak poprzednio- prostokątami), na których ta granica jest stała prawie wszędzie.
Widzimy więc że jest to ten sam dowód co poprzednio; należy tylko wskazać pokrycie ![]() zbiorami otwartymi (odpowiednikami wcześniejszych ”prostokątów”), dla których będziemy umieli udowodnić że odpowiednia granica jest stała prawie wszędzie.
Weźmy więc punkt
zbiorami otwartymi (odpowiednikami wcześniejszych ”prostokątów”), dla których będziemy umieli udowodnić że odpowiednia granica jest stała prawie wszędzie.
Weźmy więc punkt ![]() . Załóżmy że w punkcie
. Załóżmy że w punkcie ![]() istnieje granica 13.1 Z poprzedniego wykłądu wiemy jak wygląda rozmaitość stabilna punktu
istnieje granica 13.1 Z poprzedniego wykłądu wiemy jak wygląda rozmaitość stabilna punktu ![]() ; jest to rzut na
; jest to rzut na ![]() odpowiedniego horocyklu (”wchodzącego”) - razem z jego wektorami normalnymi. Punkt
odpowiedniego horocyklu (”wchodzącego”) - razem z jego wektorami normalnymi. Punkt ![]() należy oczywiscie do tego horocyklu (a raczej: jego podniesienia w
należy oczywiscie do tego horocyklu (a raczej: jego podniesienia w ![]() ). Dla wszystkich punktów
). Dla wszystkich punktów ![]() z rozmaitości stabilnej
z rozmaitości stabilnej ![]() granica
13.1 istnieje i jest równa granicy policzonej w punkcie
granica
13.1 istnieje i jest równa granicy policzonej w punkcie ![]() .
Słaba rozmaitość stabilna to suma wchodzących horocykli, wypuszczonych z wszystkich punktów
.
Słaba rozmaitość stabilna to suma wchodzących horocykli, wypuszczonych z wszystkich punktów ![]() leżących na geodezyjnej wyznaczonej przez
leżących na geodezyjnej wyznaczonej przez ![]() .
.
Zauważmy że granica 13.1 jest ![]() - niezmiennicza, więc istnieje i jest równa granicy policzonej w
- niezmiennicza, więc istnieje i jest równa granicy policzonej w ![]() , również we wszystkich punktach
, również we wszystkich punktach ![]() należących do słabej rozmaitości stabilnej
należących do słabej rozmaitości stabilnej ![]() .
.
Podobnie jak poprzednio, wykazujemy że jeśli ![]() są blisko
są blisko ![]() to można je połączyć ”łancuszkiem ” rozmaitości stabilnych i niestabilnych i wykazać istnienie i równość granic 13.1 w punktach
to można je połączyć ”łancuszkiem ” rozmaitości stabilnych i niestabilnych i wykazać istnienie i równość granic 13.1 w punktach ![]() i
i ![]() .
.
rysunek
∎13.3. Potoki geodezyjne na wybranych powierzchniach; przykłady całkowalnych potoków geodezyjnych
W tym rozdziale opiszemy potoki na kilku naturalnych (dobrze znanych, i zanurzalnych izometrycznie w ![]() ) powierzchniach. Ich własności są zupełnie inne niż opisane w poprzednim rozdziale własności potoków na powierzchniach o ujemniej krzywiźnie.
) powierzchniach. Ich własności są zupełnie inne niż opisane w poprzednim rozdziale własności potoków na powierzchniach o ujemniej krzywiźnie.
13.3.1. Potok geodezyjny na sferze
Stwierdzenie 13.1
Geodezyjne na sferze ![]() są kołami wielkimi. Potok geodezyjny na wiązce sfer stycznych do
są kołami wielkimi. Potok geodezyjny na wiązce sfer stycznych do ![]() to ruch ze stała (co do długości wektora) prędkością po kole wielkim. Zatem- każda trajektoria jest okresowa. Potok geodezyjny nie jest więc oczywiście ergodyczny.
to ruch ze stała (co do długości wektora) prędkością po kole wielkim. Zatem- każda trajektoria jest okresowa. Potok geodezyjny nie jest więc oczywiście ergodyczny.
Niech ![]() będzie dowolną geodezyjną. Ustalmy punkt
będzie dowolną geodezyjną. Ustalmy punkt ![]() i koło wielkie
i koło wielkie ![]() , które zawiera punkt
, które zawiera punkt ![]() i dla którego jednostkowy wektor styczny w punkcie
i dla którego jednostkowy wektor styczny w punkcie ![]() pokrywa sie z
pokrywa sie z ![]() . Rozważmy symetrię względem płaszczyzny wyznaczonej przez koło wielkie
. Rozważmy symetrię względem płaszczyzny wyznaczonej przez koło wielkie ![]() . Jest to oczywiście, po obcięciu do sfery, izometria w metryce sferycznej.
Symetria ta zachowuje koło wielkie
. Jest to oczywiście, po obcięciu do sfery, izometria w metryce sferycznej.
Symetria ta zachowuje koło wielkie ![]() , a geodezyjną
, a geodezyjną ![]() przekształca na geodezyjną, przechodzącą przez ten sam punkt
przekształca na geodezyjną, przechodzącą przez ten sam punkt ![]() i styczną w punkcie
i styczną w punkcie ![]() do tego samego co
do tego samego co ![]() wektora. Stąd wynika ( z jednoznacznego wyznaczenia geodezyjnej przez punkt i wektor styczny) że obrazem
wektora. Stąd wynika ( z jednoznacznego wyznaczenia geodezyjnej przez punkt i wektor styczny) że obrazem ![]() przy symetrii jest
przy symetrii jest ![]() , z zachowaniem parametryzacji, więc krzywa
, z zachowaniem parametryzacji, więc krzywa ![]() jest zawarta w zbiorze punktów stałych naszej symetrii. Zatem- jest to koło wielkie, po którym ruch odbywa się ze stała prędkością.
jest zawarta w zbiorze punktów stałych naszej symetrii. Zatem- jest to koło wielkie, po którym ruch odbywa się ze stała prędkością.
13.3.2. Potok geodezyjny na torusie 
Torus utożsamiamy z przestrzenią ilorazową:
![]() działa na
działa na ![]() jako grupa izometrii przestrzeni euklidesowej
jako grupa izometrii przestrzeni euklidesowej ![]() , gdzie
, gdzie ![]() .
Możemy zatem wprowadzić indukowaną metrykę na torusie; jest to jedyna metryka przy której rzutowanie
.
Możemy zatem wprowadzić indukowaną metrykę na torusie; jest to jedyna metryka przy której rzutowanie ![]() jest lokalną izometrią.
jest lokalną izometrią.
Ćwiczenie 13.1
Torus jest ”lepiej znany” jako obiekt (powierzchnia opony) zanurzony w ![]() . Na takim zanurzonym torusie mamy metrykę Riemannowską dziedziczoną z
. Na takim zanurzonym torusie mamy metrykę Riemannowską dziedziczoną z ![]() (długość wektora stycznego to długość zmierzona w
(długość wektora stycznego to długość zmierzona w ![]() , długość drogi na torusie też mierzymy licząc po prostu długość w
, długość drogi na torusie też mierzymy licząc po prostu długość w ![]() . Wyjaśnić w jaki sposób torus -przestrzeń ilorazową utożsamiamy z torusem- ”oponą” i jak mają się do siebie te dwie, róznie wprowadzone, metryki.
. Wyjaśnić w jaki sposób torus -przestrzeń ilorazową utożsamiamy z torusem- ”oponą” i jak mają się do siebie te dwie, róznie wprowadzone, metryki.
Stwierdzenie 13.2
Geodezyjne na torusie pokrywają się z rzutami (przy kanonicznym rzutowaniu ![]() ) prostych w
) prostych w ![]() .
.
Najpierw sprawdzamy że geodezyjnymi na płaszczyźnie są wszystkie proste. Na przykład- tak samo jak dla geodezyjnych na sferze (należy użyć symetrii osiowej zamiast symetrii względem płaszczyzny). Ponieważ rzutowanie jest lokalną izometrią, obrazami (i przeciwobrazami)geodezyjnych są geodezyjne.
∎Wniosek 13.1
Potok geodezyjny na wiązce sfer ![]() nie jest ergodyczny. Istotnie, możemy podzielić wiązkę
nie jest ergodyczny. Istotnie, możemy podzielić wiązkę ![]() na dwa niezmiennicze podozbiory dodatniej miary:
Rozatrzmy w
na dwa niezmiennicze podozbiory dodatniej miary:
Rozatrzmy w ![]() zbiór
zbiór ![]() i
i ![]() .
Zbiory
.
Zbiory ![]() i
i ![]() są niezmiennicze przy potoku geodezyjnym w
są niezmiennicze przy potoku geodezyjnym w ![]() , zatem
, zatem ![]() i
i ![]() są niezmiennicze przy potoku geodezyjnym na
są niezmiennicze przy potoku geodezyjnym na ![]() .
.




