Zagadnienia
15. O entropii topologicznej
15.1. Definicja entropii
Ograniczymy się do zdefiniowania entropii topologicznej dla ciągłego przekształcenia zwartej przestrzeni metrycznej.
Zatem-![]() jest przestrzenią zwartą metryczną z metryką
jest przestrzenią zwartą metryczną z metryką ![]() ,
, ![]() - ciągłym przekształceniem.
- ciągłym przekształceniem.
Definicja 15.1
Odległość ![]() między punktami
między punktami ![]() to
to
Definicja 15.2
Mówimy że punkty ![]() są
są ![]() - rozdzielone, jeśli
- rozdzielone, jeśli
![]() . Zbiór punktów
. Zbiór punktów ![]() - rozdzielonych to zbiór w którym każde dwa różne elementy są
- rozdzielonych to zbiór w którym każde dwa różne elementy są ![]() - rozdzielone.
- rozdzielone.
Definicja 15.3
Mówimy że punkty ![]() stanowią
stanowią ![]() -sieć jeśli dla każdego
-sieć jeśli dla każdego ![]() istnieje
istnieje ![]() takie że
takie że ![]() .
.
Oznaczmy przez ![]() maksymalną liczebność zbioru
maksymalną liczebność zbioru ![]() - rozdzielonego, a przez
- rozdzielonego, a przez
![]() - minimalną liczebność
- minimalną liczebność ![]() -sieci.
-sieci.
Definicja 15.4 (Definicja entropii topologicznej)
Entropia topologiczna ![]() jest to
jest to
Ta definicja wymaga uzasadnienia: po pierwsze- w każdej z tych dwóch formuł trzeba sprawdzić czy istnieje granica ![]() , po drugie- że obie formuły prowadzą do tego samego wyniku.
Sprawdzenie jest zawarte w Stwierdzeniu - poniżej. Dowód pozostawiamy jako ćwiczenie.
, po drugie- że obie formuły prowadzą do tego samego wyniku.
Sprawdzenie jest zawarte w Stwierdzeniu - poniżej. Dowód pozostawiamy jako ćwiczenie.
Stwierdzenie 15.1
Mamy:
Ponadto, dla ![]() mamy
mamy ![]() ,
, ![]()
Przykład 15.1 (Izometria)
Niech ![]() będzie izometrią, na przykład- obrotem na okręgu. Wówczas
będzie izometrią, na przykład- obrotem na okręgu. Wówczas ![]() . Istotnie, ustalmy
. Istotnie, ustalmy ![]() i jakąś
i jakąś ![]() sieć (w naszej notacji jest to
sieć (w naszej notacji jest to ![]() - sieć
- sieć ![]() o liczebości
o liczebości ![]() . Ponieważ
. Ponieważ ![]() jest izometrią, ten sam zbiór
jest izometrią, ten sam zbiór ![]() jest też
jest też ![]() - siecią. Zatem liczebność minimalnej
- siecią. Zatem liczebność minimalnej ![]() sieci nie rośnie z
sieci nie rośnie z ![]() . Stąd
. Stąd ![]() .
.
Ćwiczenie 15.1 (Przekształcenie 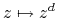 )
)
Sprawdzić że entropia tego przekształcenie jest równa ![]() . Wskazówka: dla ustalonego
. Wskazówka: dla ustalonego ![]() możemy podzielić okrąg na
możemy podzielić okrąg na ![]() łuków, z których każdy jest przekształcany (rozciągany) przez
łuków, z których każdy jest przekształcany (rozciągany) przez ![]() na cały okrąg. W każdym takim łuku wybieramy
na cały okrąg. W każdym takim łuku wybieramy ![]() równo odległych punktów. Te wszystkie punkty (jest ich razem
równo odległych punktów. Te wszystkie punkty (jest ich razem ![]() ) stanowią zbiór
) stanowią zbiór ![]() -rozdzielony.
-rozdzielony.
Ćwiczenie 15.2 (Trudniejsza wersja)
Niech ![]() będzie Riemannowską zwartą rozmaitościa, a
będzie Riemannowską zwartą rozmaitościa, a ![]() - rozszerzającym przekształceniem, tzn istnieje
- rozszerzającym przekształceniem, tzn istnieje ![]() takie że
takie że ![]() . Uzasadnić że wówczas
. Uzasadnić że wówczas ![]() jest nakryciem; niech
jest nakryciem; niech ![]() będzie stopniem tego nakrycia. Wykazać że
będzie stopniem tego nakrycia. Wykazać że ![]() .
.
Ćwiczenie 15.3
Niech ![]() będzie hiperbolicznym automorfizmem torusa
będzie hiperbolicznym automorfizmem torusa ![]() . Wówczas macierz
. Wówczas macierz ![]() reprezentująca
reprezentująca ![]() ma dwie rzeczywiste wartości własne
ma dwie rzeczywiste wartości własne ![]() . Wykazać że
. Wykazać że ![]() .
.
Stwierdzenie 15.2
Jeśli ![]() są przestrzeniami metrycznymi zwartymi,
są przestrzeniami metrycznymi zwartymi, ![]() ,
, ![]() są sprzężone topologicznie, to
są sprzężone topologicznie, to ![]() .
.
Ustalmy ![]() . Istnieje
. Istnieje ![]() takie że
takie że ![]() .
Wynika stąd że jeśli
.
Wynika stąd że jeśli ![]() jest zbiorem
jest zbiorem ![]() rozdzielonym dla
rozdzielonym dla ![]() , to
, to ![]() jest zbiorem
jest zbiorem ![]() - rozdzielonym dla
- rozdzielonym dla ![]() . Zatem
. Zatem
Stąd już łatwo wynika że ![]() .
.
15.2. Związki z entropią metryczną
Następujące dwa twierdzenia podajemy bez dowodu:
Twierdzenie 15.1 (Twierdzenie Goodwyna)
Niech ![]() będzie zwartą przestrzenią metryczną,
będzie zwartą przestrzenią metryczną, ![]() - ciągłym przekształceniem,
- ciągłym przekształceniem,
![]() - miarą borelowską probabilistyczną na
- miarą borelowską probabilistyczną na ![]() , niezmienniczą dla
, niezmienniczą dla ![]() . Wówczas:
. Wówczas:
Wzmocnieniem jest silniejsze twierdzenie
Twierdzenie 15.2 (Twierdzenie Goodmana)
Przy poprzednich założeniach, mamy
gdzie supremum jest wzięte po wszystkich niezmienniczych borelowskich miarach probabilistycznych.
15.3. Związki ze stopniem przekształcenia
Definicja 15.5
Niech ![]() będzie zwartą, zorientowaną rozmaitością gładką,
będzie zwartą, zorientowaną rozmaitością gładką, ![]() - gładkim przekształceniem.
Na
- gładkim przekształceniem.
Na ![]() mamy więc naturalną miarę Lebesge'a.
Niech
mamy więc naturalną miarę Lebesge'a.
Niech ![]() będzie wartością regularną (tw Sarda gwarantuje że jest to zbiór pełnej miary).
Stopniem przekształcenia
będzie wartością regularną (tw Sarda gwarantuje że jest to zbiór pełnej miary).
Stopniem przekształcenia ![]() w
w ![]() nazywamy
nazywamy
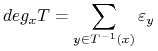 |
gdzie ![]() jest równe
jest równe ![]() lub
lub ![]() w zależności od tego czy
w zależności od tego czy ![]() zmienia czy zachowuje orientację.
zmienia czy zachowuje orientację.
Uwaga 15.1
Można sprawdzić że w istocie, stopień ![]() nie zależy od wyboru punktu
nie zależy od wyboru punktu ![]() - wartości regularnej.
Zatem- możemy zdefiniowac
- wartości regularnej.
Zatem- możemy zdefiniowac ![]() - jako wspólną wartość
- jako wspólną wartość ![]() dla wszystkich wartości regularnych
dla wszystkich wartości regularnych ![]() .
.
Twierdzenie 15.3 (Misiurewicz, Przytycki)
Jeśli ![]() jest gładką orientowalną rozmaitością, a
jest gładką orientowalną rozmaitością, a ![]() - przekzstałceniem klasy
- przekzstałceniem klasy ![]() to
to ![]() .
.




