Zagadnienia
4. Przekształcenia odcinka. Chaos na odcinku
4.1. O poszukiwaniu punktów okresowych dla przekształceń odcinka
Rozpatrzmy ciągłe przekształcenie ![]() gdzie
gdzie ![]() jest odcinkiem domkniętym.
jest odcinkiem domkniętym.
Mówimy że odcinek (domknięty) ![]() nakrywa odcinek domknięty
nakrywa odcinek domknięty ![]() jeśli
jeśli ![]() .
Oznaczenie:
.
Oznaczenie: ![]() .
.
Lemat 4.1
Niech ![]() będą odcinkami. Załóżmy że
będą odcinkami. Załóżmy że ![]() . Wówczas istnieje domknięty odcinek
. Wówczas istnieje domknięty odcinek ![]() taki że
taki że ![]() .
.
Oznaczmy odcinek ![]() przez
przez ![]() . Weźmy
. Weźmy ![]() ,
, ![]() . Jeśli takie
. Jeśli takie ![]() istnieje, odcinek
istnieje, odcinek ![]() jest szukanynm odcinkiem
jest szukanynm odcinkiem ![]() . Jeśli takie
. Jeśli takie ![]() nie istnieje (wartośc
nie istnieje (wartośc ![]() nie jest przyjmowana na prawo od
nie jest przyjmowana na prawo od ![]() ),to istnieje
),to istnieje ![]() takie że
takie że ![]() . Wybieramy największe
. Wybieramy największe ![]() o takiej własności. Jesli wartość
o takiej własności. Jesli wartość ![]() nie jest przyjmowana w odcinku
nie jest przyjmowana w odcinku ![]() , to jest to nasz szukany odcinek
, to jest to nasz szukany odcinek ![]() . W przeciwnym razie- modyfikujemy (zmniejszamy)
. W przeciwnym razie- modyfikujemy (zmniejszamy) ![]() , zastępując je najmniejszym
, zastępując je najmniejszym ![]() takim że
takim że ![]() .
.
Lemat 4.2
Jeśli ![]() to
to ![]() ma punkt stały w
ma punkt stały w ![]() .
.
Korzystamy z poprzedniego lematu. Mamy odcinek ![]() taki że
taki że ![]() ,
, ![]() . Zatem funkcja
. Zatem funkcja ![]() zmienia znak w odcinku
zmienia znak w odcinku ![]() , a stąd- istnieje punkt
, a stąd- istnieje punkt ![]() taki że
taki że ![]()
Przez prostą indukcję dostajemy następujące uogólnienie Lematu 4.1
Lemat 4.3
Jeśli
to w odcinku ![]() można znaleźć odcinek
można znaleźć odcinek ![]() taki że
taki że ![]() .
.
Znajdujemy odcinek ![]() taki że
taki że ![]() . Ponieważ
. Ponieważ ![]() więc istnieje odcinek
więc istnieje odcinek ![]() taki że
taki że ![]() . Zatem
. Zatem ![]() i istnieje odcinek
i istnieje odcinek ![]() taki że
taki że ![]() , czyli
, czyli ![]() . Dalej postępujemy przez indukcje: mamy już
. Dalej postępujemy przez indukcje: mamy już ![]() takie że
takie że ![]() ; skoro
; skoro ![]() to istnieje
to istnieje ![]() takie że
takie że ![]() . Wówczas
. Wówczas ![]() (przy
(przy ![]() ) więc istnieje
) więc istnieje ![]() takie że
takie że ![]() , czyli
, czyli ![]() .
.
Wniosek 4.1
Jeśli
to istnieje punkt okresowy ![]() o okresie
o okresie ![]() taki że
taki że ![]() .
.
Ostatni wniosek służy do ”produkowania” orbit okresowych o zadanej trajektorii.
Udowodnimy następujące twierdzenie, pochodzące od Li i Yorka.
Twierdzenie 4.1 (”Okres 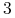 implikuje chaos”)
implikuje chaos”)
Załóżmy że ![]() ciągła i że
ciągła i że ![]() ma punkt o okresie
ma punkt o okresie ![]() . Wówczas
. Wówczas ![]() ma punkty okresowe o wszystkich okresach.
ma punkty okresowe o wszystkich okresach.
Oznaczmy orbitę o okresie ![]() przez
przez ![]() . Załóżmy że
. Załóżmy że ![]() . Oznaczmy
. Oznaczmy ![]() .
Wówczas, skoro
.
Wówczas, skoro ![]() , mamy
, mamy ![]() .
Zatem możemy z naszym przekształceniem związać graf o dwóch wierzchołkach
.
Zatem możemy z naszym przekształceniem związać graf o dwóch wierzchołkach ![]() i strzałkach
i strzałkach ![]() .
Po pierwsze, zauważmy że skoro
.
Po pierwsze, zauważmy że skoro ![]() , to z wniosku powyżej wynika że
, to z wniosku powyżej wynika że ![]() ma punkt stały zawarty w odcinku
ma punkt stały zawarty w odcinku ![]() .
.
Każdej pętli w grafie odpowiada jakiś punkt okresowy. Rozważmy więc pętlę
![]() . Z wniosku 4.1 wynika że istnieje orbita okresowa
. Z wniosku 4.1 wynika że istnieje orbita okresowa ![]() taka że
taka że ![]() ,
, ![]() dla
dla ![]() . Sprawdzimy że
. Sprawdzimy że ![]() jest okresem podstawowym dla
jest okresem podstawowym dla ![]() . Jeśli
. Jeśli ![]() dla pewnego
dla pewnego ![]() , to (biorąc pod uwagę że jeden z tych punktów leży w
, to (biorąc pod uwagę że jeden z tych punktów leży w ![]() a drugi w
a drugi w ![]() ),
), ![]() musi być wspólnym końcem odcinków
musi być wspólnym końcem odcinków ![]() i
i ![]() ,
, ![]() . To jednak jest niemożliwe. Istotnie, jeśli
. To jednak jest niemożliwe. Istotnie, jeśli ![]() to
to ![]() podczas gdy
podczas gdy ![]() . Jeśli zaś
. Jeśli zaś ![]() to sprzeczność wynika z faktu że
to sprzeczność wynika z faktu że ![]() , podczas gdy
, podczas gdy ![]() .
.
4.2. Twierdzenie Szarkowskiego
W latach sześćdziesiątych ukraiński matematyk Szarkowski wykazał że istnieje pewien niestandardowy porządek liniowy w zbiorze liczb naturalnych, ”rządzacy” pojawianiem się punktów okresowych dla funkcji ciągłych określonych na odcinku.
Zaczniemy od wprowadzenia tego porządku.
Definicja 4.1
Porządek Szarkowskiego:
Najpierw liczby nieparzyste większe niż ![]() ustawiamy w porządku malejącym:
ustawiamy w porządku malejącym:
Następnie pojawiają się w tym porządku wszystkie liczby będące iloczynem dwójki i liczby nieparzystej (zaczynając od ![]() ), liczby postaci
), liczby postaci ![]() liczba nieparzysta etc.
liczba nieparzysta etc.
Mamy więc
W ten sposób uporządkowane zostały wszystkie liczby poza potęgami dwójki. Ustawiamy je na końcu, w porządku malejącym
Zatem: największą liczbą w tym porządku jest ![]() , zaś najmniejszą
, zaś najmniejszą ![]() .
.
Możemy teraz sformułować
Twierdzenie 4.2
Twierdzenie Szarkowskiego.
Niech ![]() będzie funkcją ciągłą. Wówczas, jeśli
będzie funkcją ciągłą. Wówczas, jeśli ![]() ma punkt o okresie (podstawowym)
ma punkt o okresie (podstawowym) ![]() , to
, to ![]() ma punkty o wszystkich okresach mniejszych (w porządku Szarkowskiego) od
ma punkty o wszystkich okresach mniejszych (w porządku Szarkowskiego) od ![]() .
.
Uwaga 4.1
Oczywiście twierdzenie 4.1 jest szczególnym przypadkiem twierdzenia Szarkowskiego. Liczba ![]() jest największa w porządku Szarkowskiego, zatem istnienie punktu o okresie
jest największa w porządku Szarkowskiego, zatem istnienie punktu o okresie ![]() implikuje istnienie punktów o wszystkich innych okresach.
implikuje istnienie punktów o wszystkich innych okresach.
4.3. Bifurkacja podwajania okresu. Obserwacja Feigenbauma
Z twierdzenia Szarkowskiego wynika że istnienie jednych orbit okresowych wynika istnienie innych i ze ”najwczesniejszymi” orbitami okresowymi sa orbity o okresach będących potęgami ![]() .
W ”modelowej” rodzinie przekształeceń odcinka
.
W ”modelowej” rodzinie przekształeceń odcinka ![]() ,
, ![]() obserwujemy pojawianie się kolejnych orbit okresowych o okresach
obserwujemy pojawianie się kolejnych orbit okresowych o okresach ![]() ; dokładniej- bifurkacja polega na tym że orbita okresowa przyciągająca o okresie
; dokładniej- bifurkacja polega na tym że orbita okresowa przyciągająca o okresie ![]() staje się odpychająca (pochodna iteracji ma moduł większy od
staje się odpychająca (pochodna iteracji ma moduł większy od ![]() ), a blisko niej - tworzy się nowa orbita przyciągająca, o dwukrotnie dluższym okresie.
Niech
), a blisko niej - tworzy się nowa orbita przyciągająca, o dwukrotnie dluższym okresie.
Niech ![]() oznacza parametr w którym pojawia się orbita okresowa o okresie
oznacza parametr w którym pojawia się orbita okresowa o okresie ![]() . Feigenbaum zauważył (choć nie umiał tego udowodnić) że ilorazy
. Feigenbaum zauważył (choć nie umiał tego udowodnić) że ilorazy
| (4.1) |
mają prawdopodobnie granicę. Zauważył też że ta granica pozostaje niezmieniona gdy rodzinę funkcji ![]() zastąpił inną rodziną. Tę wspólną granicę ciągów (4.1) nazywa się stałą Feigenbauma.
zastąpił inną rodziną. Tę wspólną granicę ciągów (4.1) nazywa się stałą Feigenbauma.
Badania nad wyjaśnieniem tego zjawiska doprowadziły do rozpatrywania tzw. operatora renormalizacji (zdefiniowanego w odpowiedniej przestrzeni funkcji), wykazania istnienia punktu stałego dla tego operatora i hiperboliczności tego punktu stałego, oraz badania tzw rozmaitości stabilnej w tym punkcie. (Pojęcie hiperboliczności i rozmaitości stabilnych dla przekształceń określonych w ![]() bądź na rozmaitości pojawi sie w następnych rozdziałach; opis problemu renormalizacji wykracza jednak poza zakres tego wykładu).
bądź na rozmaitości pojawi sie w następnych rozdziałach; opis problemu renormalizacji wykracza jednak poza zakres tego wykładu).




