Zagadnienia
5. Pola wektorowe na rozmaitościach. Zbiory graniczne i zbiór punktów niebłądzących. Pola gradientowe
Będziemy mówili o trajektoriach pola wektorowego na rozmaitości ![]() zanurzonej w
zanurzonej w ![]() .
Będziemy również zakładali że rozmaitość
.
Będziemy również zakładali że rozmaitość ![]() jest zwarta. Z twierdzenia o przedłużaniu rozwiązań wynika że wówczas potok pola wektorowego
jest zwarta. Z twierdzenia o przedłużaniu rozwiązań wynika że wówczas potok pola wektorowego ![]() jest określony dla wszystkich czasów
jest określony dla wszystkich czasów ![]() . Mamy więc jednoparametrową rodzinę dyfeomorfizmów określonych na rozmiatości
. Mamy więc jednoparametrową rodzinę dyfeomorfizmów określonych na rozmiatości ![]() .
.
Duża część rozważań ma jednak charakter lokalny, więc wystarczy wtedy wykazać odpowiednie twierdzenia dla pola określonego na otwartym podzbiorze ![]() i skorzystać z następującej obserwacji:
i skorzystać z następującej obserwacji:
Stwierdzenie 5.1 (O trajektoriach pola w parametryzacji)
Niech ![]() będzie polem wektorowym określonym na gładkiej,
będzie polem wektorowym określonym na gładkiej, ![]() -wymiarowej rozmaitości
-wymiarowej rozmaitości ![]() zanurzonej w
zanurzonej w ![]() .
Niech
.
Niech ![]() bedzie parametryzacją otwartego podzbioru
bedzie parametryzacją otwartego podzbioru ![]() .
. ![]() jest zatem określone na otwartym podzbiorze
jest zatem określone na otwartym podzbiorze ![]() .
Rozważmy pole
.
Rozważmy pole ![]() , czyli
, czyli ![]() określone na otwartym podzbiorze
określone na otwartym podzbiorze ![]() wzorem:
wzorem:
Wówczas ![]() jest krzywą całkową równania
jest krzywą całkową równania ![]() wtedy i tylko wtedy gdy
wtedy i tylko wtedy gdy
![]() jest krzywą całkową równania
jest krzywą całkową równania ![]() .
.
Załóżmy że:
Sprawdzamy że
Mamy
Dowód odwrotnej implikacji jest analogiczny.
∎5.1. Zachowanie asymptotyczne trajektorii. Zbiór  -graniczny.
-graniczny.
Definicja 5.1
Niech ![]() bedzie polem wektorowym na rozmaitości gładkiej zwartej
bedzie polem wektorowym na rozmaitości gładkiej zwartej ![]() ,
, ![]() - potokiem tego pola. Mówimy że
- potokiem tego pola. Mówimy że ![]() jest punktem
jest punktem ![]() - granicznym trajektorii
- granicznym trajektorii ![]() ,
, ![]() jeśli istnieje ciąg czasów
jeśli istnieje ciąg czasów ![]() taki że
taki że
Twierdzenie 5.1 (Własności zbioru  -granicznego)
-granicznego)
Niech ![]() będzie polem wektorowym klasy
będzie polem wektorowym klasy ![]() na zwartej rozmaitości
na zwartej rozmaitości ![]() . Niech
. Niech ![]() . Wówczas:
. Wówczas:
-
-
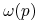 jest domkniętym podzbiorem
jest domkniętym podzbiorem 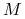 .
. -
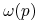 jest niezmienniczym (ze względu na potok pola
jest niezmienniczym (ze względu na potok pola 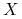 ) podzbiorem
) podzbiorem 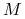 , to znaczy
, to znaczy 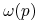 jest sumą pewnych trajektorii pola
jest sumą pewnych trajektorii pola 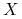 .
. -
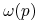 jest zbiorem spójnym.
jest zbiorem spójnym.
Pierwsza własność wynika natychmiast ze zwartości ![]() . Druga własność wynika z następującej obserwacji:
jeśli
. Druga własność wynika z następującej obserwacji:
jeśli ![]() jest potokiem pola
jest potokiem pola ![]() i
i ![]() dla pewnego ciągu
dla pewnego ciągu ![]() , to
, to
zatem ![]() . Spójność wykażemy niewprost: załózmy że
. Spójność wykażemy niewprost: załózmy że ![]() jest sumą dwóch
rozłącznych domkniętych zbiorów
jest sumą dwóch
rozłącznych domkniętych zbiorów ![]() . Ponieważ są to domknięte rozłaczne podzbiory, możemy znależć otoczenia
. Ponieważ są to domknięte rozłaczne podzbiory, możemy znależć otoczenia ![]() ,
, ![]() takie że
takie że ![]() . Ponieważ
. Ponieważ ![]() więc istnieje ciąg
więc istnieje ciąg ![]() taki że
taki że ![]() . Ponieważ
. Ponieważ ![]() , dla każdego
, dla każdego ![]() znajdzie się
znajdzie się ![]() taki że
taki że ![]() . Zatem (pamietamy że
. Zatem (pamietamy że ![]() jest zwarty) istnieje punkt
jest zwarty) istnieje punkt ![]() w
w ![]() . Otrzymujemy sprzeczność.
. Otrzymujemy sprzeczność.
Przykład 5.1 (Obmotka na torusie)
Rozpatrzmy stałe pole wektorowe na ![]() :
: ![]() .
Trajektorie tego pola w
.
Trajektorie tego pola w ![]() to oczywiście proste
to oczywiście proste ![]() .
To samo pole można rozważać na torusie - przestrzeni ilorazowej
.
To samo pole można rozważać na torusie - przestrzeni ilorazowej ![]() .
Trajektoriami na torusie są linie powstałe jako rzutowania prostych
.
Trajektoriami na torusie są linie powstałe jako rzutowania prostych ![]() . Jeślli iloraz
. Jeślli iloraz ![]() jest liczbą wymierną tokażda trajektoria na torusie jest okresowa. Jeśli iloraz jest niewymierny to każda trajektoria jest gęsta. W tym drugim przypadku mamy:
jest liczbą wymierną tokażda trajektoria na torusie jest okresowa. Jeśli iloraz jest niewymierny to każda trajektoria jest gęsta. W tym drugim przypadku mamy: ![]() dla każdego
dla każdego ![]() .
.
Definicja 5.2 (Zbiór punktów niebłądzących 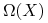 .)
.)
Mówimy że punkt ![]() jest błądzący jeśli istnieje jego otoczenie
jest błądzący jeśli istnieje jego otoczenie ![]() i
i ![]() że dla każdego
że dla każdego ![]() mamy
mamy ![]() . Uzupelnienie zbioru punktów błądzących nazywamy zbiorem punktów niebłądzących i oznaczamy
. Uzupelnienie zbioru punktów błądzących nazywamy zbiorem punktów niebłądzących i oznaczamy ![]() .
.
Uwaga 5.1
Zbiór ![]() jest niezmienniczy ze względu na dzialanie pola
jest niezmienniczy ze względu na dzialanie pola ![]() (tzn
(tzn ![]() ) i domknięty.
) i domknięty.
Uwaga 5.2
Oczywiście zbiór ![]() jest zawarty w
jest zawarty w ![]() .
.
5.2. Pola gradientowe
Przykład- potoki gradientowe
Niech ![]() będzie gładką
będzie gładką ![]() - wymiarową podrozmaitością zanurzoną w
- wymiarową podrozmaitością zanurzoną w ![]() .
W przestrzeni stycznej do
.
W przestrzeni stycznej do ![]() mamy zdefiniowany iloczyn skalarny i normę dziedziczoną z
mamy zdefiniowany iloczyn skalarny i normę dziedziczoną z ![]() .
(Mamy więc strukturę Riemannowska dziedziczona z
.
(Mamy więc strukturę Riemannowska dziedziczona z ![]() ).
).
Niech ![]() będzie funkcją klasy
będzie funkcją klasy ![]() . Wówczas różniczka
. Wówczas różniczka ![]() w punkcie
w punkcie ![]() ,
, ![]() jest
jest ![]() - formą (przekształceniem liniowym
- formą (przekształceniem liniowym ![]() . Zatem istnieje dokładnie jeden wektor
. Zatem istnieje dokładnie jeden wektor ![]() w przestrzeni stycznej
w przestrzeni stycznej ![]() , taki że
, taki że ![]() . Ten wektor nazywamy gradientem funkcji
. Ten wektor nazywamy gradientem funkcji ![]() w punkcie
w punkcie ![]() .
Otrzymujemy w ten sposób pole wektorowe klasy
.
Otrzymujemy w ten sposób pole wektorowe klasy ![]() na
na ![]() .
Jeśli funkcja
.
Jeśli funkcja ![]() jest określona nie tylko w
jest określona nie tylko w ![]() , ale również na otoczeniu
, ale również na otoczeniu ![]() w
w ![]() , to łatwo można związać gradient
, to łatwo można związać gradient ![]() ze zwykłym wektorem gradientu w
ze zwykłym wektorem gradientu w ![]() .
Możemy policzyć ”zwykłą” różniczkę
.
Możemy policzyć ”zwykłą” różniczkę ![]() w
w ![]() ,
, ![]() , i ”zwykły” gradient
, i ”zwykły” gradient ![]() .
Wówczas dla
.
Wówczas dla ![]()
Zatem ![]() (gradient
(gradient ![]() ”wzdłuż” rozmaitości
”wzdłuż” rozmaitości ![]() jest rzutem prostopadłym gradientu policzonego w przestrzeni
jest rzutem prostopadłym gradientu policzonego w przestrzeni ![]() ,
, ![]() , na przestrzeń styczną do
, na przestrzeń styczną do ![]() .
.
Definicja 5.3
Punkt ![]() jest punktem osobliwym pola wektorowego
jest punktem osobliwym pola wektorowego ![]() jeśli
jeśli ![]() .
.
Stwierdzenie 5.2 (Własności pola gradientowego)
Niech ![]() będzie gładką rozmaitością,
będzie gładką rozmaitością, ![]() -funkcją klasy
-funkcją klasy ![]() na
na ![]() ,zaś
,zaś ![]() - gradientowym polem wektorowym (klasy
- gradientowym polem wektorowym (klasy ![]() na
na ![]() .
Wówczas
.
Wówczas
-
Pole gradientowe
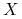 nie ma trajektorii zamkniętych.
nie ma trajektorii zamkniętych. -
Dla każdego
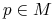 zbiór
zbiór 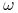 - graniczny
- graniczny 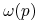 jest zawarty w zbiorze punktów osobliwych pola
jest zawarty w zbiorze punktów osobliwych pola 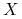 .
.
Zauważmy że dla każdej trajektorii pola ![]() mamy:
mamy:
Zatem funkcja ![]() jest niemalejąca wzdłuż każdej trajektorii, a dokładniej- ściśle rosnąca wzdłuż każdej ”niestacjonarnej trajektorii”.
jest niemalejąca wzdłuż każdej trajektorii, a dokładniej- ściśle rosnąca wzdłuż każdej ”niestacjonarnej trajektorii”.
Wynika stąd oczywiście że pole nie ma orbit zamkniętych.
Załóżmy teraz że punkt ![]() i
i ![]() .
Wowczas w otoczeniu punktu
.
Wowczas w otoczeniu punktu ![]() poziomica
poziomica ![]() funkcji
funkcji ![]() przechodząca przez
przechodząca przez ![]() jest podrozmaitością
jest podrozmaitością ![]() prostopadła do linii pola
prostopadła do linii pola ![]() . Z twierdzenia o prostowaniu trajektorii wynika że każda trajektoria pola startujaca dostatecznie blisko punktu
. Z twierdzenia o prostowaniu trajektorii wynika że każda trajektoria pola startujaca dostatecznie blisko punktu ![]() musi przeciąć poziomicę
musi przeciąć poziomicę ![]() . Jeśli
. Jeśli ![]() to trajektoria
to trajektoria ![]() ,
, ![]() musi zatem przeciąć nieskończenie wiele razy poziomicę
musi zatem przeciąć nieskończenie wiele razy poziomicę ![]() . Ponieważ jednak, jak już wiemy, funkcja
. Ponieważ jednak, jak już wiemy, funkcja ![]() jest ściśle rosnąca wzdłuż tej trajektorii, jest to oczywiście niemożliwe.
jest ściśle rosnąca wzdłuż tej trajektorii, jest to oczywiście niemożliwe.
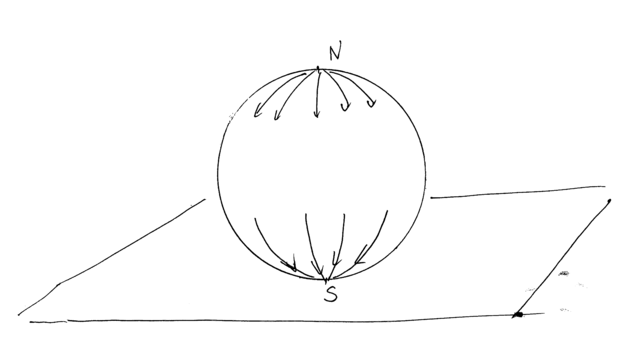
Przykład 5.2
Pole gradient wysokości na sferze. To pole ma dwa punkty osobliwe ![]() i
i ![]() . Punkt
. Punkt ![]() jest źródłem, punkt
jest źródłem, punkt ![]() -ściekiem. Dla każdego punktu
-ściekiem. Dla każdego punktu ![]() mamy
mamy ![]() (rysunek 5.1)
(rysunek 5.1)
Przykład 5.3
Pole wektorowe gradientowe na postawionym torusie.
Tu ![]() . To pole ma cztery punkty stacjonarne:
. To pole ma cztery punkty stacjonarne: ![]() .
. ![]() jest źródłem,
jest źródłem, ![]() -ściekiem,
-ściekiem, ![]() - siodłami. Zauważmy że tym razem zbiór
- siodłami. Zauważmy że tym razem zbiór ![]() - graniczny zależy od punktu, w szczególności istnieją punkty dla ktorych
- graniczny zależy od punktu, w szczególności istnieją punkty dla ktorych ![]() jest siodłem. Istnieja też połączenia między siodlami- trajektorie
jest siodłem. Istnieja też połączenia między siodlami- trajektorie ![]() takie że dla
takie że dla ![]()
![]() , zaś dla
, zaś dla ![]()
![]() . (rysunek 5.2).
. (rysunek 5.2).
5.3. Cięcia transwersalne i przekształcenie Poincare'go w otoczeniu orbity okresowej
Rozważmy pole wektorowe ![]() klasy
klasy ![]() określone (dla uproszczenia) w otwartym podzbiorze
określone (dla uproszczenia) w otwartym podzbiorze ![]() . Niech
. Niech ![]() będzie zamkniętą trajektorią tego pola,
będzie zamkniętą trajektorią tego pola, ![]() - okresem tej trajektorii,
- okresem tej trajektorii, ![]() . Możemy założyć że
. Możemy założyć że ![]() .
Rozważmy hiperpowierzchnię
.
Rozważmy hiperpowierzchnię ![]() . Zatem pole jest w punkcie
. Zatem pole jest w punkcie ![]() transwersalne do
transwersalne do ![]() .
Dla
.
Dla ![]() bliskich
bliskich ![]() trajektoria pola wychodząca z
trajektoria pola wychodząca z ![]() wróci po czasie bliskim
wróci po czasie bliskim ![]() do
do ![]() . Formalne sprawdzenie:
Niech
. Formalne sprawdzenie:
Niech ![]() będzie potokiem pola
będzie potokiem pola ![]() , określamy funkcję
, określamy funkcję
Wówczas ![]() i
i ![]() .
.
Mamy
Zatem- z twierdzenia o funkcji uwikłanej wynika że istnieje otoczenie ![]() w
w ![]() w którym to równanie wyznacza
w którym to równanie wyznacza ![]() jako funkcję
jako funkcję ![]() , tej samej klasy co
, tej samej klasy co ![]() . Oznaczamy tę funkcję
. Oznaczamy tę funkcję ![]() .
.
Mamy więc w otoczeniu ![]() w
w ![]() zdefiniowane przekształcenie klasy
zdefiniowane przekształcenie klasy ![]() :
:
Nazywamy je przekształceniem Poincare'go, oznaczenie: ![]() .
.
Pytamy o związek między wartościami własnymi dla pochodnej przekształcenia Poincare'go w punkcie ![]() i różniczki potoku pola:
i różniczki potoku pola: ![]() .
.
Wiemy już że jedną z wartości własnych ![]() jest
jest ![]() , bo
, bo ![]() .
.
Twierdzenie 5.2
Wartości własne różniczki ![]() , różne od
, różne od ![]() , są takie same jak wartości własne rózniczki
, są takie same jak wartości własne rózniczki ![]() .
.
W ![]() wprowadzamy układ współrzędnych, w którym jednym z wektorów bazowych jest
wprowadzamy układ współrzędnych, w którym jednym z wektorów bazowych jest ![]() , a pozostałe wektory- to baza
, a pozostałe wektory- to baza ![]() .
Weźmy wektor styczny dla
.
Weźmy wektor styczny dla ![]() , ma on postać (w układzie współrzędnych w
, ma on postać (w układzie współrzędnych w ![]() z wyróżnioną ostatnią współrzędną)
z wyróżnioną ostatnią współrzędną) ![]() .
Różniczka
.
Różniczka ![]() w tej bazie to
w tej bazie to
| (5.1) |
Tutaj ![]() jest macierzą
jest macierzą ![]() . Przekształcenie Poincarego
. Przekształcenie Poincarego ![]() .
Zatem
.
Zatem
Skądinąd wiemy że obrazem ![]() musi byc wektor styczny do
musi byc wektor styczny do ![]() , więc współrzedna w kierunku pola
, więc współrzedna w kierunku pola ![]() znika i ostatecznie
znika i ostatecznie
To zaś oznacza że ![]() ma takie same wartości własne jak różne od
ma takie same wartości własne jak różne od ![]() wartości własne
wartości własne ![]() .
.
Definicja 5.4
Mówimy że orbita okresowa ![]() , o okresie
, o okresie ![]() pola
pola ![]() jest hiperboliczna jeśli dla punktu
jest hiperboliczna jeśli dla punktu ![]() różniczka
różniczka ![]() ma tylko jedną -pojedynczą wartość własną równą
ma tylko jedną -pojedynczą wartość własną równą ![]() .
Równoważnie- jeśli dla cięcia Poincare'go
.
Równoważnie- jeśli dla cięcia Poincare'go ![]() różniczka przekształcenia Poincare'go
różniczka przekształcenia Poincare'go ![]() nie ma wartości własnych różnych od
nie ma wartości własnych różnych od ![]() .
.