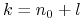Zagadnienia
7. Pola Morse'a-Smale'a. Dyfeomorfizmy Morse'a- Smale'a.  -eksplozja i podkowa Smale'a
-eksplozja i podkowa Smale'a
7.1. Pola wektorowe i dyfeomorfizmy Morse'a- Smale'a
Definicja 7.1
Niech ![]() będzie zwartą rozmaitością wymiaru
będzie zwartą rozmaitością wymiaru ![]() , zaś
, zaś ![]() - polem wektorowym klasy
- polem wektorowym klasy ![]() na
na ![]() . Mówimy że
. Mówimy że ![]() jest polem Morse'a-Smale'a jeśli
jest polem Morse'a-Smale'a jeśli
-
1
 ma skończenie wiele elementów krytycznych i wszystkie elementy krytyczne są hiperboliczne.
ma skończenie wiele elementów krytycznych i wszystkie elementy krytyczne są hiperboliczne. -
2 Jeśli
 ,
, 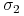 są elementami krytycznymi, to rozmaitości
są elementami krytycznymi, to rozmaitości 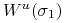 ,
, 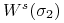 przecinają się transwersalnie.
przecinają się transwersalnie. -
3
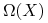 - zbiór punktów niebłądzących- jest sumą elementów krytycznych.
- zbiór punktów niebłądzących- jest sumą elementów krytycznych.
Dla dyfeomorfizmów mamy odpowiednio definicję:
Definicja 7.2
Dyfeomorfizm ![]() jest dyfeomorfizmem Morse'a-Smale'a jeśli:
jest dyfeomorfizmem Morse'a-Smale'a jeśli:
-
1 f ma skończenie wiele punktów okresowych i wszystkie są hiperboliczne.
-
2 Wszystkie przecięcia
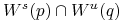 są transwersalne
są transwersalne -
3
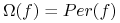
Jak wiemy, jeśli ![]() jest polem wektorowym na zwartej rozmaitości, to
jest polem wektorowym na zwartej rozmaitości, to ![]() generuje rodzinę dyfeomorfizmów (potok pola)
generuje rodzinę dyfeomorfizmów (potok pola) ![]() .
Warto w tym miejscu zastanowić się czy jeśli
.
Warto w tym miejscu zastanowić się czy jeśli ![]() jest polem Morse'a Smale'a to dyfeomorfizm
jest polem Morse'a Smale'a to dyfeomorfizm ![]() jest dyfeomorfizmem Morse'a Smale'a.
Łatwo sprawdzić że mamy
jest dyfeomorfizmem Morse'a Smale'a.
Łatwo sprawdzić że mamy
Ćwiczenie 7.1
Niech ![]() będzie polem wektorowym Morse'a -Smale'a na zwartej gładkiej rozmaitości
będzie polem wektorowym Morse'a -Smale'a na zwartej gładkiej rozmaitości ![]() . Wówczas dyfeomorfizm
. Wówczas dyfeomorfizm ![]() (
(![]() ) jest dyfeomorfizmem Morse'a Smale'a wtedy i tylko wtedy gdy
) jest dyfeomorfizmem Morse'a Smale'a wtedy i tylko wtedy gdy ![]() nie ma orbit zamkniętych (tzn zbiór elementów krytycznych
nie ma orbit zamkniętych (tzn zbiór elementów krytycznych ![]() składa się tylko z punktów krytycznych).
składa się tylko z punktów krytycznych).
W rozdziale trzecim uzyskaliśmy pełną charakteryzację ![]() strukturalnie stabilnych dyfeomorfizmów i pól wektorowych na okręgu (okazało się że są to dokładnie pola wektorowe i dyfeomorfizmy Morse'a - Smale'a). Zatem- naturalne jest pytanie czy te wyniki przenoszą sie na przypadek wyższych wymiarów.
strukturalnie stabilnych dyfeomorfizmów i pól wektorowych na okręgu (okazało się że są to dokładnie pola wektorowe i dyfeomorfizmy Morse'a - Smale'a). Zatem- naturalne jest pytanie czy te wyniki przenoszą sie na przypadek wyższych wymiarów.
Mamy następujące twierdzenie, wykazane przez J. Palisa (nie będziemy go tu dowodzić):
Twierdzenie 7.1 (O otwartości zbiorów dyfeomorfizmów i pól wektorowych Morse'a-Smale'a)
Niech ![]() będzie gładką zwartą rozmaitościa. Wówczas dla każdego
będzie gładką zwartą rozmaitościa. Wówczas dla każdego ![]() zbiór dyfeomorfizmów Morse'a -Smale'a klasy
zbiór dyfeomorfizmów Morse'a -Smale'a klasy ![]() jest niepusty oraz otwarty w przestrzeni
jest niepusty oraz otwarty w przestrzeni ![]() . Podobnie, zbiór pól wektorowych Morse'a -Smale'a klasy
. Podobnie, zbiór pól wektorowych Morse'a -Smale'a klasy ![]() jest niepusty i otwarty w przestrzeni
jest niepusty i otwarty w przestrzeni ![]() pól wektorowych klasy
pól wektorowych klasy ![]() na
na ![]() .
.
Twierdzenie 7.2
Jeśli ![]() jest polem Morse'a -Smale'a to
jest polem Morse'a -Smale'a to ![]() jest (
jest (![]() ) strukturalnie stabilne. Podobnie, jeśli
) strukturalnie stabilne. Podobnie, jeśli ![]() jest dyfeomorfizmem Morse'a -Smale'a to
jest dyfeomorfizmem Morse'a -Smale'a to ![]() jest strukturalnie stabilne.
jest strukturalnie stabilne.
Różnica pomiędzy sytuacją jednowymiarową (okrąg) a ogólną polega jednak na tym, że w ogólnym przypadku dyfeomorfizmy i pola wektorowe Morse'a Smale'a nie stanowią zbioru gęstego i nie wypełniają wszystkich przykładów strukturalnie stabilnych.
7.2. 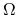 -eksplozja
-eksplozja
Zajmiemy się teraz opisaniem ważnego przykładu (który jednocześnie pokazuje dlaczego w wyższych wymiarach nie można spodziewać się gęstości dyfeomorfizmów Morse'a-Smale'a.
Twierdzenie 7.3 (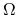 -eksplozja)
-eksplozja)
Na rozmaitości ![]() wymiaru
wymiaru ![]() dyfeomorfizmy Morse'a-Smale'a nie są gęste w przestrzeni dyfeomorfizmów
dyfeomorfizmy Morse'a-Smale'a nie są gęste w przestrzeni dyfeomorfizmów ![]() .
.
szkic
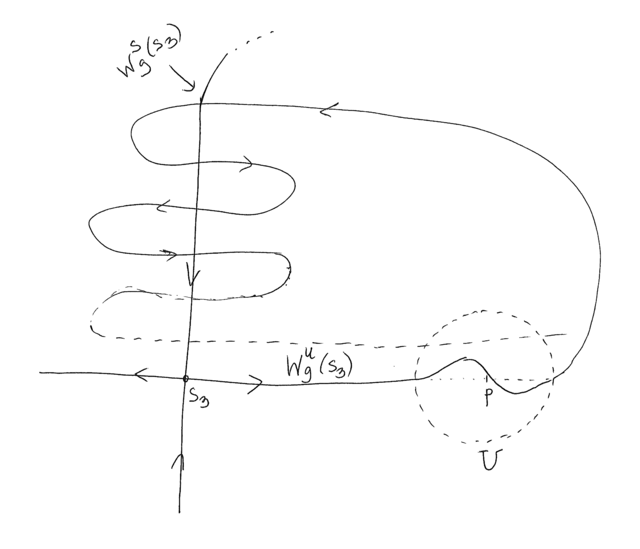
Rozważamy na sferze ![]() pole wektorowe
pole wektorowe ![]() które ma cztery punkty krytyczne. Punkty
które ma cztery punkty krytyczne. Punkty ![]() i
i ![]() są ściekami, punkt
są ściekami, punkt ![]() jest siodłem, zaś
jest siodłem, zaś ![]() -źródłem. Ponadto istnieje trajektoria dla której zbiorem
-źródłem. Ponadto istnieje trajektoria dla której zbiorem ![]() i
i ![]() -granicznym jest ten sam punkt
-granicznym jest ten sam punkt ![]() - bowiem globalne rozmaitości stabilna i niestabilna punktu
- bowiem globalne rozmaitości stabilna i niestabilna punktu ![]() pokrywają się. Niech
pokrywają się. Niech ![]() będzie potokiem tego pola; oznaczmy przez
będzie potokiem tego pola; oznaczmy przez ![]() ”dyfeomorfizm po czasie 1”.
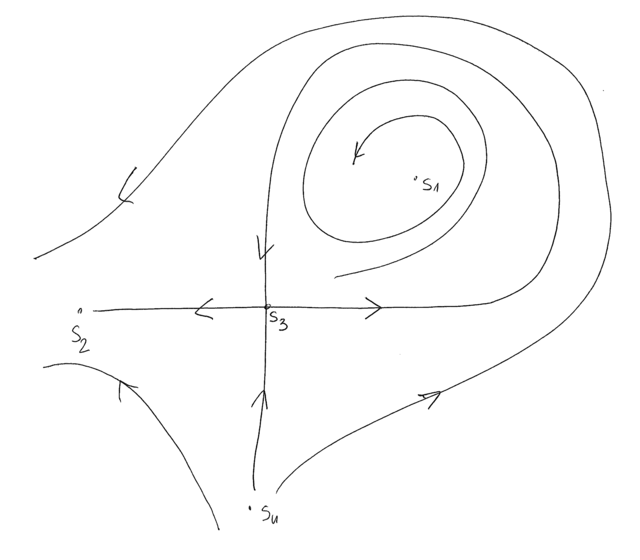
Na rysunkach 7.1 i 7.2 przedstawiono portret fazowy wyjściowego pola wektorowego (widziany na płaszczyźnie i na sferze).
”dyfeomorfizm po czasie 1”.
Na rysunkach 7.1 i 7.2 przedstawiono portret fazowy wyjściowego pola wektorowego (widziany na płaszczyźnie i na sferze).
Zaburzymy teraz dyfeomorfizm ![]() w ten sposób że punkt
w ten sposób że punkt ![]() pozostanie siodłem, ale dla nowego zaburzonego przekształcenia (oznaczanego dalej przez
pozostanie siodłem, ale dla nowego zaburzonego przekształcenia (oznaczanego dalej przez ![]() )
) ![]() będzie przecinać się z
będzie przecinać się z ![]() transwersalnie.
transwersalnie.
Wybieramy punkt ![]() i otoczenie punktu
i otoczenie punktu ![]() takie że
takie że ![]() .
Uzyjemy ”lokalnej deformacji”- przekształcenia (dyfeomorfizmu)
.
Uzyjemy ”lokalnej deformacji”- przekształcenia (dyfeomorfizmu) ![]() takiego że
takiego że ![]() poza
poza ![]() oraz, dodatkowo,
oraz, dodatkowo, ![]() , ale
, ale ![]() przecina teraz tranwersalnie
przecina teraz tranwersalnie ![]() w punkcie
w punkcie ![]() . (Mowiąc nieformalnie,
. (Mowiąc nieformalnie, ![]() ”wykrzywilo” lokalnie rozmaitość
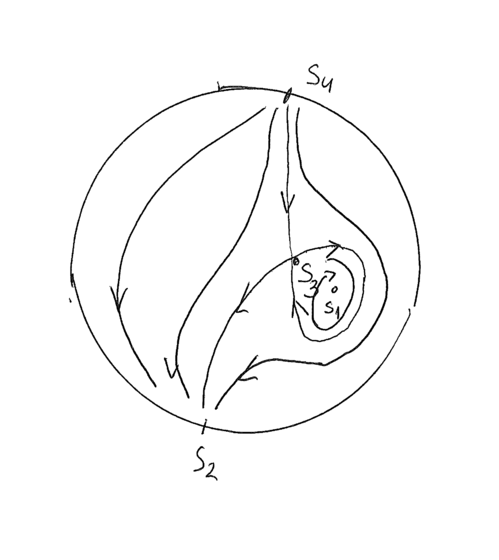
”wykrzywilo” lokalnie rozmaitość ![]() ). Na rysunkach 7.3 i 7.4 przedstawiono deformację
). Na rysunkach 7.3 i 7.4 przedstawiono deformację ![]() i
efekt jej zastosowania.
i
efekt jej zastosowania.
Rozpatrujemy teraz dyfeomorfizm ![]() . Zauważmy że
. Zauważmy że ![]() pokrywa się z
pokrywa się z ![]() poza zbiorem
poza zbiorem ![]() . W wyniku tej deformacji globalna rozmaitość niestabilna (zdefiniowana, przypomnijmy, jako
. W wyniku tej deformacji globalna rozmaitość niestabilna (zdefiniowana, przypomnijmy, jako ![]() zmienia się w otoczeniu punktu
zmienia się w otoczeniu punktu ![]() (dokładniej- ten fragment rozmaitości niestabilnej, który jest zawarty w
(dokładniej- ten fragment rozmaitości niestabilnej, który jest zawarty w ![]() zostanie zastąpiony przez jego obraz przy przekształceniu
zostanie zastąpiony przez jego obraz przy przekształceniu ![]() ). Natomiast fragment rozmaitości stabilnej
). Natomiast fragment rozmaitości stabilnej ![]() zawarty w
zawarty w ![]() pozostanie niezmieniony. Pojawi się zatem w punkcie
pozostanie niezmieniony. Pojawi się zatem w punkcie ![]() transwersalne przecięcie rozmaitości stabilnej i niestabilnej (rysunki 7.3 i 7.4).
transwersalne przecięcie rozmaitości stabilnej i niestabilnej (rysunki 7.3 i 7.4).
Zauważamy teraz
Stwierdzenie 7.1
Punkt ![]() jest niebłądzacy dla zaburzonego przekształcenia
jest niebłądzacy dla zaburzonego przekształcenia ![]() .
.
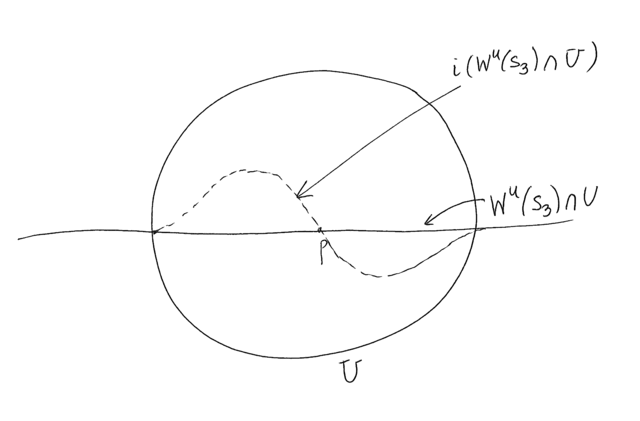
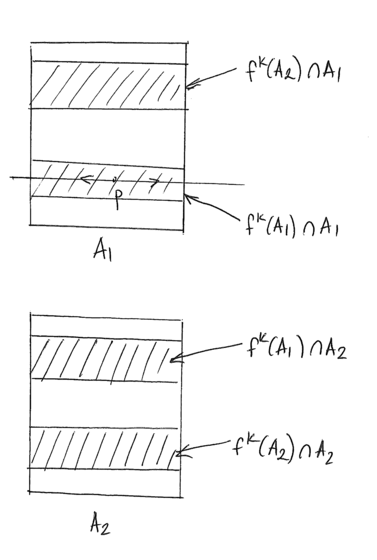
Niech ![]() będzie małym otoczeniem
będzie małym otoczeniem ![]() ;
; ![]() niech będzie fragmentem rozmaitości niestabilnej
niech będzie fragmentem rozmaitości niestabilnej ![]() zawartym w
zawartym w ![]() . Rozpatrujemy kolejne obrazy
. Rozpatrujemy kolejne obrazy ![]() przy przekształceniu
przy przekształceniu ![]() (rysunek 7.4).
Rysunek pokazuje że obrazy ( a dokladniej: ich fragmenty) zbliżają się do fragmentu rozmaitości niestabilnej zawartego między punktami
(rysunek 7.4).
Rysunek pokazuje że obrazy ( a dokladniej: ich fragmenty) zbliżają się do fragmentu rozmaitości niestabilnej zawartego między punktami ![]() i
i ![]() i układają ”równolegle” do niego. Zatem- muszą przeciąć
i układają ”równolegle” do niego. Zatem- muszą przeciąć ![]() . Formalny dowód wymaga wykorzystania tzw
. Formalny dowód wymaga wykorzystania tzw ![]() -lematu, którego sformułowanie podajemy na końcu tego wykładu.
-lematu, którego sformułowanie podajemy na końcu tego wykładu.
Możemy teraz wyjaśnić dlaczego opisane tu zjawisko nazywa się ![]() -ekspozją. Zauważmy że wyjsciowe pole wektorowe
-ekspozją. Zauważmy że wyjsciowe pole wektorowe ![]() miało bardzo prosty zbiór punktów niebłądzących
miało bardzo prosty zbiór punktów niebłądzących ![]() . Również dyfeomorfizm
. Również dyfeomorfizm ![]() ma ten sam zbiór punktów niebłądzących. Z konstrukcji wynika że możemy dowolnie mało zaburzyć
ma ten sam zbiór punktów niebłądzących. Z konstrukcji wynika że możemy dowolnie mało zaburzyć ![]() (i to zaburzenie możemy uczynić małym w
(i to zaburzenie możemy uczynić małym w ![]() topologii) tak aby pojawił się dodatkowy punkt niebłądzący. Naprawde, tych nowych punktów niebłądzących pojawi się więcej- są to przynajmniej wszystkie obrazy i przeciwobrazy
topologii) tak aby pojawił się dodatkowy punkt niebłądzący. Naprawde, tych nowych punktów niebłądzących pojawi się więcej- są to przynajmniej wszystkie obrazy i przeciwobrazy ![]() . W następnym rozdziale (7.4) wykażemy że, w istocie zbiór punktów niebłądzących dla
. W następnym rozdziale (7.4) wykażemy że, w istocie zbiór punktów niebłądzących dla ![]() jest nieprzeliczalny.
jest nieprzeliczalny.
Oczywiscie ![]() nie jest dyfeomorfizmem Morse'a Smale'a. Aby dokończyć dowód wystarczy wykazać że istnieje otoczenie
nie jest dyfeomorfizmem Morse'a Smale'a. Aby dokończyć dowód wystarczy wykazać że istnieje otoczenie ![]() w
w ![]() topologii złożone z dyfeomorfizmów, które również nie są Morse'a Smale'a. Wystarczy w tym celu wykazać
topologii złożone z dyfeomorfizmów, które również nie są Morse'a Smale'a. Wystarczy w tym celu wykazać
Stwierdzenie 7.2
Jeśli ![]() jest dyfeomorfizmem odpowiednio bliskim dyfeomorfizmowi
jest dyfeomorfizmem odpowiednio bliskim dyfeomorfizmowi ![]() w
w ![]() topologii, to
topologii, to ![]() ma punkt stały
ma punkt stały ![]() bliski
bliski ![]() , będący też siodłem i rozmaitości niestabilna i stabilna (dla
, będący też siodłem i rozmaitości niestabilna i stabilna (dla ![]() i siodła
i siodła ![]() ) przecinają się traswersalnie.
) przecinają się traswersalnie.
Istotnie, ze Stwierdzenia 7.2 wynika że żaden dyfeomorfizm ![]() nie jest Morse'a -Smale'a (bo ma punkty niebładzące- punkty przecięcia rozmaitości stabilnej i niestabilnej dla siodła) które nie są okresowe.
nie jest Morse'a -Smale'a (bo ma punkty niebładzące- punkty przecięcia rozmaitości stabilnej i niestabilnej dla siodła) które nie są okresowe.
7.3.  lemat
lemat
Niech ![]() będzie punktem stałym (okresowym) hiperbolicznym dyfeomrofizmu
będzie punktem stałym (okresowym) hiperbolicznym dyfeomrofizmu ![]() na rozmaitości
na rozmaitości ![]() wymiarowej
wymiarowej ![]() .
Wprowadźmy w otoczeniu
.
Wprowadźmy w otoczeniu ![]() układ współrzędnych taki że
układ współrzędnych taki że ![]() jest w tym układzie obrazem
jest w tym układzie obrazem ![]() .
W tym układzie współrzędnych rozmaitości stabilna i niestabilna punktu
.
W tym układzie współrzędnych rozmaitości stabilna i niestabilna punktu ![]() są podrozmaitościami stycznymi w
są podrozmaitościami stycznymi w ![]() odpowiednio do
odpowiednio do ![]() ,
, ![]() .
.
![]() jest wykresem funkcji
jest wykresem funkcji ![]() (gdzie
(gdzie ![]() jest otoczeniem zera w
jest otoczeniem zera w ![]() ) takiej ze
) takiej ze ![]() , podobnie
, podobnie ![]() jest wykresem funkcji
jest wykresem funkcji ![]() (gdzie
(gdzie ![]() jest otoczeniem zera w
jest otoczeniem zera w ![]() ), takiej ze
), takiej ze ![]() .
.
Wówczas przekształcenie
jest dyfeomorfizmem przekształcającym ![]() na otoczenie zera w
na otoczenie zera w ![]() , zaś
, zaś ![]() na otoczenie zera w
na otoczenie zera w ![]() .
W tych współrzędnych najłatwiej jest sformułowac
.
W tych współrzędnych najłatwiej jest sformułowac ![]() lemat:
lemat:
Twierdzenie 7.4 ( -lemat)
-lemat)
Niech ![]() (w opisanym układzie współrzędnych; zatem
(w opisanym układzie współrzędnych; zatem ![]() ,
, ![]() ). Rozważmy
). Rozważmy ![]() i immersyjnie zanurzony dysk
i immersyjnie zanurzony dysk ![]() o wymiarze
o wymiarze ![]() , transwersalny do
, transwersalny do ![]() w punkcie
w punkcie ![]() .
.
Oznaczmy przez ![]() tę spójną składową
tę spójną składową ![]() , do której należy punkt
, do której należy punkt ![]() .
.
Wówczas dla każdego ![]() istnieje
istnieje ![]() takie że jeśli
takie że jeśli ![]() to
to ![]() jest
jest ![]() bliskie
bliskie ![]() (to znaczy: jest wykresem funkcji
(to znaczy: jest wykresem funkcji ![]() o wartościach i pochodnej mniejszych co do normy od
o wartościach i pochodnej mniejszych co do normy od ![]() )
)
rysunek
![]() -lemat mówi więc że każdy dyski
-lemat mówi więc że każdy dyski ![]() , po odpowiedniu dalekiej iteracji, ma w obrazie podzbiór otwarty ”prawie równoległy” do
, po odpowiedniu dalekiej iteracji, ma w obrazie podzbiór otwarty ”prawie równoległy” do ![]() .
.
7.4. Podkowa Smale'a
Najpierw zdefiniujemy pewien układ dynamiczny w przestrzeni symbolicznej.
Definicja 7.3
Niech ![]() będzie liczbą naturalną niech
będzie liczbą naturalną niech
W przestrzeni ![]() określamy odległość: jeśli
określamy odległość: jeśli ![]() to
to
gdzie ![]() jest największą liczbą naturalną taką że
jest największą liczbą naturalną taką że ![]() .
Jeśli takie
.
Jeśli takie ![]() nie istnieje, to kładziemy
nie istnieje, to kładziemy ![]() .
W przestrzeni
.
W przestrzeni ![]() mamy naturalne przekształcenie
mamy naturalne przekształcenie ![]() - przesunięcie w lewo:
- przesunięcie w lewo:
Opiszemy teraz dyfeomorfizm sfery ![]() który ma interesujący podzbiór niezmienniczy.
który ma interesujący podzbiór niezmienniczy.
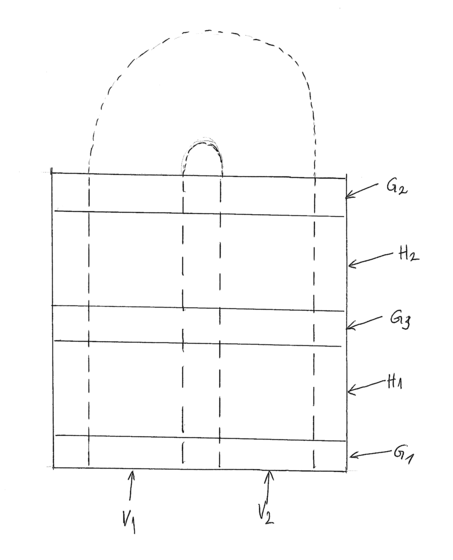
Zaczynamy od kwadratu ![]() . W tym kwadracie wyróżniamy dwa rozłaczne pozome prostokąty:
. W tym kwadracie wyróżniamy dwa rozłaczne pozome prostokąty:
![]() i
i ![]() oraz dwa rozłaczne pionowe prostokąty
oraz dwa rozłaczne pionowe prostokąty ![]() i
i ![]() , położone jak na rysunku
, położone jak na rysunku
Chcemy aby dyfeomorfizm ![]() przekształcał
przekształcał ![]() na
na ![]() ,
, ![]() na
na ![]() afinicznie, i aby
afinicznie, i aby ![]() .
Nieformalnie mówiąc- rozciągamy wzdłuż kwadrat
.
Nieformalnie mówiąc- rozciągamy wzdłuż kwadrat ![]() , a otrzymany prostokąt zginamy w ”podkowę” (rysunek 7.5).
, a otrzymany prostokąt zginamy w ”podkowę” (rysunek 7.5).
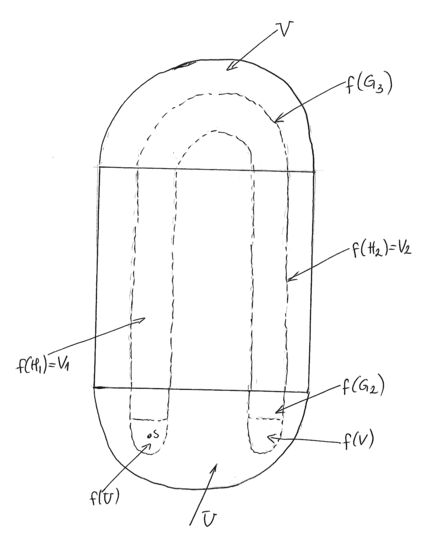
Aby rozszerzyc takie przekształcenie, doklejamy do kwadratu dwa topologiczne dyski (np półkola) ![]() , i
, i ![]() (otrzymujemy w ten sposób nowy dysk topologiczny
(otrzymujemy w ten sposób nowy dysk topologiczny ![]() tak że
tak że ![]() ,
,
![]() ,
, ![]() . Teraz trzeba jeszcze zdefiniować
. Teraz trzeba jeszcze zdefiniować ![]() na
na ![]() i na
i na ![]() . Obrazy tych połkoli są przedstawione na rysunku 7.6.
. Obrazy tych połkoli są przedstawione na rysunku 7.6.
![]() jest zdefiniowane na
jest zdefiniowane na ![]() w ten sposób że wewnątrz
w ten sposób że wewnątrz ![]() jest umieszczony punkt stały przyciągający
jest umieszczony punkt stały przyciągający ![]() i
i ![]() .
Wynika stąd że dla każdego
.
Wynika stąd że dla każdego ![]() (a także dla każdego
(a także dla każdego ![]() )
) ![]() .
Mamy więc zdefiniowany dyfeomorfizm
.
Mamy więc zdefiniowany dyfeomorfizm ![]() i
i ![]() . Tak zdefiniowane przekształcenie możemy przedłużyc też do dyfeomorfizmu całej sfery
. Tak zdefiniowane przekształcenie możemy przedłużyc też do dyfeomorfizmu całej sfery ![]() (N można utożsamić przez dyfeomorfizm z górną półsferą; na dolnej półsferze
(N można utożsamić przez dyfeomorfizm z górną półsferą; na dolnej półsferze ![]() definiujemy dyfeomorfizm tak aby
definiujemy dyfeomorfizm tak aby ![]() (zatem
(zatem ![]() ), umieszczając punkt stały na przykład w biegunie południowym
), umieszczając punkt stały na przykład w biegunie południowym ![]() . Wówczas dla każdego
. Wówczas dla każdego ![]() mamy
mamy ![]() .
Z tych obserwacji wynika że zbiór punktów niebłądzących rożnych od
.
Z tych obserwacji wynika że zbiór punktów niebłądzących rożnych od ![]()
![]() jest zawarty w wyjściowym kwadracie
jest zawarty w wyjściowym kwadracie ![]() . Istotnie, jeśli
. Istotnie, jeśli ![]() to ujemna trajektoria punktu
to ujemna trajektoria punktu ![]() i całego jego otoczenia jest przyciągana do bieguna południowego
i całego jego otoczenia jest przyciągana do bieguna południowego ![]() , zatem istnieje takie otoczenie
, zatem istnieje takie otoczenie ![]() punktu
punktu ![]() że
że ![]() dla wszystkich
dla wszystkich ![]() . Podobnie, jeśli
. Podobnie, jeśli ![]() , to
, to ![]() jest przyciągane przy iteracji w przód do punkty stałego
jest przyciągane przy iteracji w przód do punkty stałego ![]() , i, z tych samych powodów
, i, z tych samych powodów ![]() jest punktem błądzącym. Ponieważ
jest punktem błądzącym. Ponieważ ![]() i zbiór punktów niebładzących
i zbiór punktów niebładzących ![]() jest niezmienniczy, więc również zbiór
jest niezmienniczy, więc również zbiór ![]() nie przecina
nie przecina ![]() .
Korzystając jeszcze raz z niezmienniczości zbioru
.
Korzystając jeszcze raz z niezmienniczości zbioru ![]() wykazaliśmy zatem
wykazaliśmy zatem
Stwierdzenie 7.3
Zbiór punktów niebłądzących ![]() jest zawarty w zbiorze
jest zawarty w zbiorze
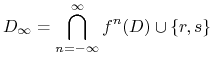 |
(zauważmy że zbiór ![]() składa się z punktów których trajektorie przez cały czas pozostają w
składa się z punktów których trajektorie przez cały czas pozostają w ![]() )
)
Wykażemy teraz że cały zbiór ![]() jest zawarty w zbiorze punktów niebłądzących
jest zawarty w zbiorze punktów niebłądzących ![]() .
W tym celu skonstruujemy sprzężenie topologiczne pomiędzy przekształceniem
.
W tym celu skonstruujemy sprzężenie topologiczne pomiędzy przekształceniem ![]() i przesunięciem w lewo
i przesunięciem w lewo ![]() na przestrzeni symbolicznej.
na przestrzeni symbolicznej.
Rozważmy zbiór
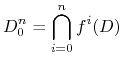 |
Widzimy (tu będzie rysunek
że ![]() jest sumą
jest sumą ![]() pionowych prostokątów, których szerokości maleją wykłądniczo z
pionowych prostokątów, których szerokości maleją wykłądniczo z ![]() ; w szczególności-
; w szczególności- ![]() jest sumą dwóch pionowych prostokątów
jest sumą dwóch pionowych prostokątów ![]() . Ponadto, w każdym prostokącie
. Ponadto, w każdym prostokącie ![]() pojawiającym się w
pojawiającym się w ![]() są zawarte dokładnie dwa prostokąty następnej generacji; przy czym suma szerokości tych prostokątów jest równa szerokości
są zawarte dokładnie dwa prostokąty następnej generacji; przy czym suma szerokości tych prostokątów jest równa szerokości ![]() pomnożonej przez
pomnożonej przez ![]() .
Zatem
.
Zatem ![]() jest produktem zbioru Cantora i odcinka. Zbiór ten składa się dokładnie z punktów które przez całą swoją historię w przeszłości pozostawaly w
jest produktem zbioru Cantora i odcinka. Zbiór ten składa się dokładnie z punktów które przez całą swoją historię w przeszłości pozostawaly w ![]() .
.
Podobnie, zbiór
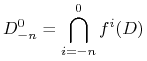 |
składa się z ![]() poziomych prostokątów; w szczególności
poziomych prostokątów; w szczególności ![]() jest to podzbiór
jest to podzbiór ![]() złożony z punktów, które w pierwszej iteracji trafiają do
złożony z punktów, które w pierwszej iteracji trafiają do ![]() .
Zbiór
.
Zbiór
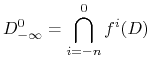 |
składa się zatem z punktów które przez cała swoją przyszłość pozostaną w ![]() ; podobnie jak poprzednio- widzimy ze jest to produkt ”pionowego” zbioru Cantora i poziomego odcinka.
; podobnie jak poprzednio- widzimy ze jest to produkt ”pionowego” zbioru Cantora i poziomego odcinka.
Oczywiście ![]() jest przecięciem tych dwóch zbiorów; jest to zatem produkt kartezjański dwóch zbiorów Cantora. W szczególności
jest przecięciem tych dwóch zbiorów; jest to zatem produkt kartezjański dwóch zbiorów Cantora. W szczególności ![]() jest zwarty.
jest zwarty.
Każdemu punktowi ![]() możemy przyporządkować jego ”kod”- nieskończony ciąg symboli
możemy przyporządkować jego ”kod”- nieskończony ciąg symboli ![]() w przestrzeni symbolicznej
w przestrzeni symbolicznej ![]() :
: ![]() jeśli
jeśli ![]() ,
, ![]() jeśli
jeśli ![]() .
.
Wykażemy
Twierdzenie 7.5
Przekształcenie ![]() jest topologicznie sprzężone z przesunięciem
jest topologicznie sprzężone z przesunięciem ![]() na przestrzeni symbolicznej
na przestrzeni symbolicznej ![]() ;
sprzężenie jest zadane przez kodowanie
;
sprzężenie jest zadane przez kodowanie ![]() :
:
Formuła ![]() wynika wprost z definicji kodowania
wynika wprost z definicji kodowania ![]() . Pozostaje więc do sprawdzenia że
. Pozostaje więc do sprawdzenia że ![]() jest homeomorfizmem.
Sprawdzimy najpierw że
jest homeomorfizmem.
Sprawdzimy najpierw że ![]() jest wzajemnie jednoznaczne. Różnowartościowość
jest wzajemnie jednoznaczne. Różnowartościowość ![]() wynika z obserwacji, że zbiór punktów które mają ten sam kod
wynika z obserwacji, że zbiór punktów które mają ten sam kod
![]() jest domkniętym prostokątem
jest domkniętym prostokątem ![]() o rozmiarach malejących wykładniczo z
o rozmiarach malejących wykładniczo z ![]() . Ponadto
. Ponadto ![]() . Zatem przecięcie jest jednopunktowe. Z konstrukcji wynika też że przekształcenie
. Zatem przecięcie jest jednopunktowe. Z konstrukcji wynika też że przekształcenie ![]() jest ”na”- każdy kod jest realizowany.
Wykażemy że
jest ”na”- każdy kod jest realizowany.
Wykażemy że ![]() jest ciągłe. Wystarczy w tym celu sprawdzić że jeśli ciąg kodów
jest ciągłe. Wystarczy w tym celu sprawdzić że jeśli ciąg kodów ![]() to ciąg odpowiadających punktów
to ciąg odpowiadających punktów
![]() . Z definicji metryki w przestrzeni
. Z definicji metryki w przestrzeni ![]() wynika że dla każdego
wynika że dla każdego ![]() istnieje takie
istnieje takie ![]() że dla każdego
że dla każdego ![]() ciągi
ciągi ![]() oraz
oraz ![]() mają te same wyrazy dla wszystkich
mają te same wyrazy dla wszystkich ![]() takich że
takich że ![]() . Stąd zaś wynika że odpowiadające im przy przekształceniu
. Stąd zaś wynika że odpowiadające im przy przekształceniu ![]() punkty leżą w tej samej spójnej składowej (prostokącie) zbioru
punkty leżą w tej samej spójnej składowej (prostokącie) zbioru ![]() .
Ponieważ długości boków tego prostokąta maleją wykłądniczo z
.
Ponieważ długości boków tego prostokąta maleją wykłądniczo z ![]() , dowodzi to zbieżności
, dowodzi to zbieżności ![]() .
Mamy więc ciągła bijekcję pomiędzy dwiema przestrzeniami metrycznymi zwartymi, zatem- homeomorfizm.
.
Mamy więc ciągła bijekcję pomiędzy dwiema przestrzeniami metrycznymi zwartymi, zatem- homeomorfizm.
Zauważmy że mamy następujące stwierdzenie (pozostawiamy dowód jako ćwiczenie)
Stwierdzenie 7.4
W przestrzeni ![]() punkty (ciągi) okresowe przy przekształceniu
punkty (ciągi) okresowe przy przekształceniu ![]() stanowią gęsty podzbiór.
stanowią gęsty podzbiór.
Stąd zaś wniosek
Wniosek 7.1
W zbiorze ![]() punkty okresowe dla
punkty okresowe dla ![]() są gęste.
są gęste.
Ponieważ każdy punkt okresowy jest zawarty w zbiorze punktów niebłądzących ![]() , i zbiór
, i zbiór ![]() jest domknięty, porównując ze Stwierdzeniem 7.3, otrzymujemy
jest domknięty, porównując ze Stwierdzeniem 7.3, otrzymujemy
Twierdzenie 7.6
Zbiór punktów niebładzących ![]() dla dyfeomorfizmu
dla dyfeomorfizmu ![]() jest równy
jest równy
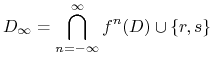 |
Punkty okresowe stanowią gęsty podzbiór ![]() .
.
do zadan: rozmaitości stabilne i niestabilne w podkowie, continuum Knastera.
Podkowa Smale'a to pewien abstrakcyjnie zdefiniowany układ dynamiczny. Jego ważność wyjaśnia poniższe twierdzenie
Twierdzenie 7.7 (Punkt homokliniczny produkuje podkowę)
Niech ![]() będzie dyfeomorfizmem rozmaitości
będzie dyfeomorfizmem rozmaitości ![]() ,
, ![]() - hiperbolicznym punktem stałym. Załóżmy że istnieje punkt homokliniczny
- hiperbolicznym punktem stałym. Załóżmy że istnieje punkt homokliniczny ![]() (czyli punkt transwersalnego przecięcia rozmaitości stabilnej
(czyli punkt transwersalnego przecięcia rozmaitości stabilnej ![]() i niestabilnej
i niestabilnej ![]() , różny od
, różny od ![]() ). Wówczas zbiór punktów niebłądzących
). Wówczas zbiór punktów niebłądzących ![]() zawiera zwarty niezmienniczy podzbiór
zawiera zwarty niezmienniczy podzbiór ![]() , homeomorficzny ze zbiorem granicznym podkowy
, homeomorficzny ze zbiorem granicznym podkowy ![]() ; homeomorfizm ten sprzęga działanie
; homeomorfizm ten sprzęga działanie ![]() z działaniem opisanego przekształcenia na podkowie.
z działaniem opisanego przekształcenia na podkowie.
Szkic dowodu
Używamy wprowadzonego powyżej układu współrzędnych. Niech ![]() .
Możemy założyć że
.
Możemy założyć że ![]() . Istotnie, jeśli
. Istotnie, jeśli ![]() jest punktem homoklinicznym to wszystkie jego obrazy- też.
Ponieważ
jest punktem homoklinicznym to wszystkie jego obrazy- też.
Ponieważ ![]() więc
więc ![]() ; zatem któryś obraz
; zatem któryś obraz ![]() leży w
leży w ![]() .
.
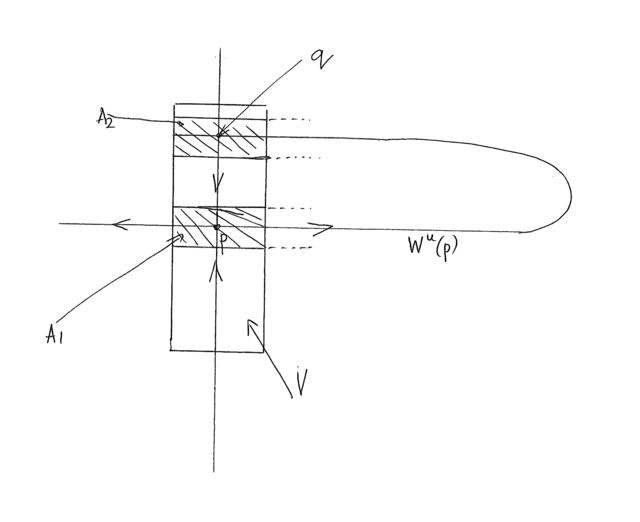
Twierdzimy że dla wszystkich odpowiednio dużych ![]() zbiór
zbiór ![]() ma co najmniej dwie składowe; punkty
ma co najmniej dwie składowe; punkty ![]() i
i ![]() należą do różnych składowych (rysunek 7.7).
należą do różnych składowych (rysunek 7.7).
Na rysunku 7.8 przestawiono przecięcie zbiorów ![]() i
i ![]() z ich kolejnymi obrazami.
W odróznieniu modelu liniowego, żadne z używanych tu przekształceń nie jest liniowe. Ponieważ używamy iteracji
z ich kolejnymi obrazami.
W odróznieniu modelu liniowego, żadne z używanych tu przekształceń nie jest liniowe. Ponieważ używamy iteracji ![]() , więc obrazy pasków mogłyby bardzo się zdeformować. Trzeba więc sprawdzić że można wybrać
, więc obrazy pasków mogłyby bardzo się zdeformować. Trzeba więc sprawdzić że można wybrać ![]() na początku tak duże że wszystkie paski pozostaną ”prawie poziome”. Wybór
na początku tak duże że wszystkie paski pozostaną ”prawie poziome”. Wybór ![]() można przeprowadzić na przykład tak:
można przeprowadzić na przykład tak:
-
Istnieje
 takie że
takie że 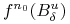 zawiera całą składową zbioru
zawiera całą składową zbioru 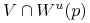 do której należy punkt
do której należy punkt 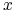 (wynika to stąd że w tych lokalnych współrzędnych
(wynika to stąd że w tych lokalnych współrzędnych 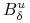 jest lokalną rozmaitością
jest lokalną rozmaitością 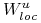 , więc
, więc
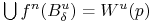 ).
). -
Ustalamy małe
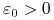 .
. -
Ustalamy
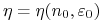 takie że obraz
takie że obraz 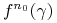 jest
jest 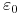 bliski (
bliski (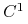 ) zbiorowi
) zbiorowi 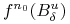 o ile
o ile 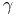 jest
jest 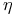 - bliskie (
- bliskie (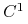 )
) 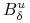 .
. -
Ustalamy
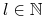 na tyle duże że każdy immersyjnie zanurzony dysk zawarty w
na tyle duże że każdy immersyjnie zanurzony dysk zawarty w 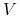 , i
, i 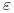 -bliski w
-bliski w 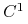 dyskowi
dyskowi 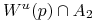 jest przekształcany przez
jest przekształcany przez 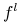 na zbiór (dysk immersyjny)
na zbiór (dysk immersyjny) 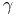 taki że
taki że 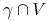 jest
jest 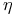 -bliskie
-bliskie 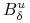 .
.Tutaj wykorzystujemy
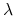 -lemat.
-lemat. -
Ustalamy