Zagadnienia
8. Zbiory hiperboliczne. Dyfeomorfizmy i potoki Anosowa. Stabilność zbiorów hiperbolicznych.
W poprzednim wykładzie opisaliśmy skomplikowany zbiór niezmienniczy dla dyfeomorfizmu- Podkowe Smale'a. Teraz opiszemy kilka innych przykładów zbiorów hiperbolicznych.
Definicja 8.1
Niech ![]() będzie dyfeomorfizmem gładkiej zwartej rozmaitości
będzie dyfeomorfizmem gładkiej zwartej rozmaitości ![]() . Zakładamy, jak zawsze w tym wykładzie, że
. Zakładamy, jak zawsze w tym wykładzie, że ![]() jest zanurzona w przestrzeni euklidesowej
jest zanurzona w przestrzeni euklidesowej ![]() , i ma, w takim razie, odziedziczoną z
, i ma, w takim razie, odziedziczoną z ![]() strukturę Riemannowska ( w szczególności, długości wektorów w przestrzeni stycznej mierzymy używając długości zmierzonej w
strukturę Riemannowska ( w szczególności, długości wektorów w przestrzeni stycznej mierzymy używając długości zmierzonej w ![]() .
.
Niech ![]() będzie zwartym niezmienniczym podzbiorem
będzie zwartym niezmienniczym podzbiorem ![]() .
Mówimy że
.
Mówimy że ![]() ma strukturę hiperboliczną jeśli
w każdym punkcie
ma strukturę hiperboliczną jeśli
w każdym punkcie ![]() zbioru
zbioru ![]() istnieje rozkład przestrzeni stycznej
istnieje rozkład przestrzeni stycznej ![]() na sumę prostą dwóch podprzestrzeni:
na sumę prostą dwóch podprzestrzeni: ![]() . Rozkład ten ma być niezmienniczy ze względu na
. Rozkład ten ma być niezmienniczy ze względu na ![]() :
:
Ponadto, żądamy aby istniały stałe ![]() takie że
takie że
dla ![]() oraz
oraz
dla ![]() .
.
Uwaga 8.1
Warto zauważyć że jeśli wektor ![]() ma (w rozkładzie na sumę prosta
ma (w rozkładzie na sumę prosta ![]() niezerową drugą składową, to długości obrazów wektora
niezerową drugą składową, to długości obrazów wektora ![]() (
(![]() ) rosną z
) rosną z ![]() wykładniczo szybko.
wykładniczo szybko.
Mamy następujące ważne Twierdzenie
Twierdzenie 8.1 (Twierdzenie o rozmaitości stabilnej dla zbiorów hiperbolicznych)
Niech ![]() będzie dyfeomorfizmem klasy
będzie dyfeomorfizmem klasy ![]() . Niech
. Niech ![]() będzie niezmienniczym zbiorem hiperbolicznym dla
będzie niezmienniczym zbiorem hiperbolicznym dla ![]() . Wówczas istnieje
. Wówczas istnieje ![]() i
i ![]() ,
, ![]() takie że dla każdego
takie że dla każdego ![]() zbiory
zbiory
oraz
są gładkimi podrozmaitościami klasy ![]() w
w ![]() .
Ponadto
.
Ponadto ![]() oraz
oraz ![]()
Uwaga 8.2
Zauważmy że równość definiująca ![]() (i podobnie
(i podobnie ![]() ) na dwa różne sposoby też wymaga dowodu!
) na dwa różne sposoby też wymaga dowodu!
do napisania
∎Definicja 8.2
Niech ![]() będzie przestrzenią metryczną.
Mówimy że odwracalne przekształcenie
będzie przestrzenią metryczną.
Mówimy że odwracalne przekształcenie ![]() jest ekspansywne jeśli istnieje
jest ekspansywne jeśli istnieje ![]() takie że dla dowolnych
takie że dla dowolnych ![]() istnieje
istnieje ![]() takie że
takie że ![]() .
.
Wniosek 8.1
Obcięcie dyfeomorfizmu do zbioru hiperbolicznego jest przekształceniem ekspansywnym.
Zauważmy że w definicji zbioru hiperbolicznego nie żądamy żeby przestrzenie ![]() zależały w sposób ciągły od punktu. Wynika to jednak z innych włąsności:
zależały w sposób ciągły od punktu. Wynika to jednak z innych włąsności:
Stwierdzenie 8.1
Przestrzenie ![]() ,
, ![]() zależą w ciągły sposób od
zależą w ciągły sposób od ![]() .
.
Weźmy ciąg punktów ![]() .
W każdej przestrzeni
.
W każdej przestrzeni ![]() wybieramy bazę ortonormalną
wybieramy bazę ortonormalną
. Przechodząc do podciągu, można założyć że
Skoro
to (z ciągłości) mamy także
Zatem, ![]() .
.
Pokazaliśmy więc że
W ten sam sposób sprawdzamy że
Skoro ![]() to musi być
to musi być
Wniosek 8.2
Podprzestrzenie ![]() i
i ![]() są ”jednostajnie transwersalne”, tzn istnieje
są ”jednostajnie transwersalne”, tzn istnieje ![]() takie że dla lażdego
takie że dla lażdego ![]() i dla dowolnych
i dla dowolnych ![]() ,
, ![]() kąt między wektorami
kąt między wektorami ![]() jest większy niż
jest większy niż ![]() .
.
Niech ![]() będzie minimalnym kątem między
będzie minimalnym kątem między ![]() ,
, ![]() . z poprzedniego stwierdzenia wynika że
. z poprzedniego stwierdzenia wynika że ![]() jest ciągłą funkcją
jest ciągłą funkcją ![]() . Ze zwartości
. Ze zwartości ![]() wynika że
wynika że ![]() .
.
Definicja 8.3
Globalna rozmaitośc stabilna (niestabilna)
Przy założeniach takich jak w poprzednim twierdzeniu definiujemy zbiory
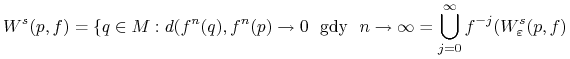 |
oraz
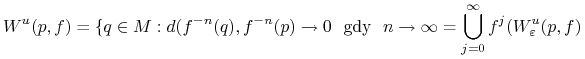 |
Zbiory te nazywamy odpowiednio globalną rozmaitością stabilną i niestabilną. Ta definicja wymaga uzasadnienia:
Ćwiczenie 8.1
Przy założeniach jak w poprzednim Twierdzeniu, wykazać że zbiory ![]() i
i ![]() są immersyjnymi podrozmaitościami klasy
są immersyjnymi podrozmaitościami klasy ![]() w
w ![]()
Ćwiczenie 8.2
Sprawdzić że podkowa Smale'a, zdefiniowana w poprzednim wykładzie, jest zbiorem hiperbolicznym.
Stwierdzenie 8.2 (Zbió hiperboliczny dla bliskiego przekształcenia)
Niech ![]() będzie zbiorem hiperbolicznym dyfeomorfizmu
będzie zbiorem hiperbolicznym dyfeomorfizmu ![]() . Wówczas istnieje otoczenie
. Wówczas istnieje otoczenie ![]() zbioru
zbioru ![]() takie że jeśli
takie że jeśli ![]() jest dyfeomorfizmem, dostatecznie bliskim (w
jest dyfeomorfizmem, dostatecznie bliskim (w ![]() metryce)
metryce) ![]() na
na ![]() , to zbiór
, to zbiór
jest hiperboliczny.
Uwaga 8.3
Nie wiemy jeszcze jak zbiór ![]() jest związany z
jest związany z ![]() , a nawet- czy jest niepusty.
, a nawet- czy jest niepusty.
Na zbiorze ![]() mamy rozkład przestrzeni stycznej
mamy rozkład przestrzeni stycznej ![]() , zależny wsposób ciągły od
, zależny wsposób ciągły od ![]() . Możemy ten rozkłąd rozszerzyć do ciągłego (niekoniecznie niezmienniczego!) na pewne otoczenie
. Możemy ten rozkłąd rozszerzyć do ciągłego (niekoniecznie niezmienniczego!) na pewne otoczenie ![]() .
.
Rozpatrujemy teraz rodzinę stożków poziomych i pionowych. Stożki poziome to
8.1. Solenoid
W tym rozdziale skonstruujemy pewien hiperboliczny atraktor (czyli zbiór który przyciąga całe swoje otoczenie). Do tej pory mielismy do czynienia z przekształceniami (lub potokami) Morse'a Smale'a, w których jedynymi atrakotrami były punkty stałe (stacjonarne) lub orbity okresowe. Ten atraktor jest zupełnie innego rodzaju.
Rozpatrzmy pełny torus ![]() . Okrąg parametryzujemy argumentem
. Okrąg parametryzujemy argumentem ![]() (
(![]() ),
zaś na dysku jednostkowym
),
zaś na dysku jednostkowym ![]() używamy zespolonej zmiennej
używamy zespolonej zmiennej ![]() .
NA okręgu rozpatrujemy przekształcenie
.
NA okręgu rozpatrujemy przekształcenie ![]() czyli
czyli ![]() Rozpatrujemy przekształcenie
Rozpatrujemy przekształcenie ![]() dane wzorem
dane wzorem
![]() przekształca zatem każdy dysk
przekształca zatem każdy dysk ![]() odpowiadający
odpowiadający ![]() na mniejszy dysk, o promieniu czterokrotnie zmniejszonym, zawarty w dysku o dwukrotnie powiększonym argumencie. Łatwo można zobaczyć jak wygląda dysk
na mniejszy dysk, o promieniu czterokrotnie zmniejszonym, zawarty w dysku o dwukrotnie powiększonym argumencie. Łatwo można zobaczyć jak wygląda dysk ![]() przecięty z obrazem
przecięty z obrazem ![]() : jest to suma dwóch rozłacznych dysków, każdy o promieniu
: jest to suma dwóch rozłacznych dysków, każdy o promieniu ![]() .
(Powstały jako obrazy odpowiednich dysków dla argumentów
.
(Powstały jako obrazy odpowiednich dysków dla argumentów ![]() i
i ![]() ).
).
rysunek
Niech ![]() .
Następujące stwierdzenie wynika łatwo z konstrukcji
.
Następujące stwierdzenie wynika łatwo z konstrukcji
Stwierdzenie 8.3
Dla każdego ![]() zbiór
zbiór
![]() jest sumą
jest sumą ![]() rozłacznych domkniętych dysków o promieniu
rozłacznych domkniętych dysków o promieniu ![]() każdy.
Dla każdego odcinka
każdy.
Dla każdego odcinka ![]() zbiór
zbiór ![]() jest sumą
jest sumą ![]() rozłącznych pełnych walców
(oczywiście mówimy o zbiorach dyfeomorficznych z walcami, nie o walcach geometrycznych).
rozłącznych pełnych walców
(oczywiście mówimy o zbiorach dyfeomorficznych z walcami, nie o walcach geometrycznych).
dwa rysunki
Niech wreszcie ![]() .
Jest to nasz atraktor; z definicji wynika że jeśli
.
Jest to nasz atraktor; z definicji wynika że jeśli ![]() to
to ![]() gdy
gdy ![]() .
Nietrudno sprawdzić że przecięcie
.
Nietrudno sprawdzić że przecięcie ![]() jest homeomorficzne ze zbiorem Cantora.
jest homeomorficzne ze zbiorem Cantora.
Wykażemy
Twierdzenie 8.2 (Własności topologiczne Solenoidu)
Zbiór ![]() ma następujące własności:
ma następujące własności:
-
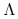 jest spójny.
jest spójny. -
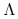 nie jest lokalnie spójny.
nie jest lokalnie spójny. -
 nie jest łukowo spójny.
nie jest łukowo spójny. -
Punkty okresowe dla
 stanowią gęsty podzbiór
stanowią gęsty podzbiór  .
. -
 jest topologicznie tranzytywne:
dla dowolnych otwartych podzbiorów
jest topologicznie tranzytywne:
dla dowolnych otwartych podzbiorów 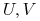 przecinających
przecinających 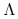 istnieje
istnieje 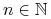 takie że
takie że 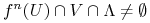 .
.
Szkic dowodu
Spójność ![]() wynika stąd że
wynika stąd że ![]() ; jest to zstępujący ciąg zbiorów zwartych i spójnych.
; jest to zstępujący ciąg zbiorów zwartych i spójnych.
Przypomnijmy że lokalna spójność oznacza że dla każdego ![]() mamy:
mamy:
. Tymczasem (rysunek) zbiór ![]() przecięty z
przecięty z ![]() jest sumą
jest sumą ![]() skręconych walców; jeśli punkty
skręconych walców; jeśli punkty ![]() należą do róznych walców to nie da się ich połączyć spójnym podzbiorem
należą do róznych walców to nie da się ich połączyć spójnym podzbiorem ![]() o małej średnicy (jedyne ”połączenie” między tymi walcami prowadzi dookoła torusa).
o małej średnicy (jedyne ”połączenie” między tymi walcami prowadzi dookoła torusa).
Wykażemy teraz że zbiór ![]() nie jest łukowo spójnym tzn że nie każde dwa punkty
nie jest łukowo spójnym tzn że nie każde dwa punkty ![]() dadzą się połaczyc
krzywą zawartą w
dadzą się połaczyc
krzywą zawartą w ![]() . Rozważmy w tym celu dysk
. Rozważmy w tym celu dysk ![]() ; oczywiście
; oczywiście ![]() .
Wybierzmy punkt
.
Wybierzmy punkt ![]() .
.
Zbiór ![]() jest sumą rodziny
jest sumą rodziny ![]() złożonej z
złożonej z ![]() dysków, które można łączyc drogami wzdłuż rozciągniętego torusa
dysków, które można łączyc drogami wzdłuż rozciągniętego torusa ![]() . Po wykonaniu jednego obrotu, trafiamy do kolejnego dysku w zbiorze
. Po wykonaniu jednego obrotu, trafiamy do kolejnego dysku w zbiorze ![]() ; po wykonaniu
; po wykonaniu ![]() obrotów- trafiamy do wyjściowego dysku. Zatem możemy wybrać punkt
obrotów- trafiamy do wyjściowego dysku. Zatem możemy wybrać punkt ![]() w tym dysku, ktory jest otrzymany z dysku zawierającego punkt
w tym dysku, ktory jest otrzymany z dysku zawierającego punkt ![]() przez
przez ![]() obrotów. Zatem- każda droga łacząca w
obrotów. Zatem- każda droga łacząca w ![]() punkty
punkty ![]() i
i ![]() musi przeciąć
musi przeciąć ![]() przynajmniej
przynajmniej ![]() razy, i wykonać pełny obrót wokół torusa pomiędzy każdymi dwoma przecieciami. W następnym kroku konstrukcji, w dysku z rodziny
razy, i wykonać pełny obrót wokół torusa pomiędzy każdymi dwoma przecieciami. W następnym kroku konstrukcji, w dysku z rodziny ![]() zawierającym
zawierającym ![]() pojawiają się na dwa dyski
z rodziny
pojawiają się na dwa dyski
z rodziny ![]() . Wybieramy ten z nich, który zawiera punkt
. Wybieramy ten z nich, który zawiera punkt ![]() ; oznaczmy go
; oznaczmy go ![]() . Podobnie, w dysku
. Podobnie, w dysku ![]() -tej generacji zawierającym
-tej generacji zawierającym ![]() pojawią się dwa dyski
pojawią się dwa dyski ![]() -szej generacji. Jeden z tych dysków da się połaczyć z
-szej generacji. Jeden z tych dysków da się połaczyć z
![]() drogą która obraca się wokół torusa
drogą która obraca się wokół torusa ![]() razy; drugi- drogą która obraca się
razy; drugi- drogą która obraca się ![]() razy. Wybieramy ten drugi, i jakiś punkt
razy. Wybieramy ten drugi, i jakiś punkt ![]() w tym dysku.
Oczywiście tak zdefiniowany ciąg
w tym dysku.
Oczywiście tak zdefiniowany ciąg ![]() jest zbieżny i jego granica
jest zbieżny i jego granica ![]() jest w
jest w ![]() .
Z konstrukcji wynika że każda droga w
.
Z konstrukcji wynika że każda droga w ![]() , łącząca
, łącząca ![]() i
i ![]() , musiałaby przecinać
, musiałaby przecinać ![]() przynajmniej
przynajmniej ![]() razy i pomiędzy dwoma przecięciami wykonać przynajmniej jeden obrót wokół torusa. Ponieważ tak musi być dla każdego
razy i pomiędzy dwoma przecięciami wykonać przynajmniej jeden obrót wokół torusa. Ponieważ tak musi być dla każdego ![]() , taka droga nie istnieje (przeczy to ciągłości drogi).
, taka droga nie istnieje (przeczy to ciągłości drogi).
Sprawdzimy gęstość orbit okresowych. Zauważmy najpierw że istnieje gęsty zbiór argumentów ![]() dla których dysk
dla których dysk ![]() jest przekształcany przez pewną iterację
jest przekształcany przez pewną iterację ![]() (zależna od
(zależna od ![]() ) w siebie (są to po prostu argumenty
) w siebie (są to po prostu argumenty ![]() odpowiadające punktom okresowym dla przekształcenia
odpowiadające punktom okresowym dla przekształcenia ![]() na okręgu). Oczywiście w każdym takim dysku znajdzie się, w takim razie, punkt stały dla
na okręgu). Oczywiście w każdym takim dysku znajdzie się, w takim razie, punkt stały dla ![]() . Zatem- w każdym zbiorze postaci
. Zatem- w każdym zbiorze postaci ![]() jest jakiś punkt okresowy dla
jest jakiś punkt okresowy dla ![]() .
Rozważmy teraz dowolne otoczenie
.
Rozważmy teraz dowolne otoczenie ![]() dowolnego punktu
dowolnego punktu ![]() . Istnieje ”cienki cylinder” - czyli zbiór postaci
. Istnieje ”cienki cylinder” - czyli zbiór postaci
![]() (dla pewnych
(dla pewnych ![]() ) zawarty w
) zawarty w ![]() (dlaczego?).
Wystarczy teraz zauważyć że
(dlaczego?).
Wystarczy teraz zauważyć że ![]() jest zbiorem postaci
jest zbiorem postaci ![]() . Zatem znajdzie się w nim jakiś punkt okresowy dla
. Zatem znajdzie się w nim jakiś punkt okresowy dla ![]() . Skoro w nim- to także w zbiorze
. Skoro w nim- to także w zbiorze ![]() , a więc- także w
, a więc- także w ![]() .
.
Stwierdzenie 8.4
![]() jest zbiorem hiperbolicznym.
jest zbiorem hiperbolicznym.
Szkic dowodu
Zapiszemy różniczkę przekształcenia ![]() we współrzędnych
we współrzędnych ![]() :
:
Wektor styczny zapisujemy jako ![]() , gdzie
, gdzie ![]() . Pod działaniem różniczki wektor
. Pod działaniem różniczki wektor ![]() jest przekształcany na wektor
jest przekształcany na wektor ![]() ; mamy więc wyznaczoną wiązkę stabilną.
Wykazanie istnienia wiązki niestabilnej jest trudniejsze. Metoda opisana poniżej nazywana jest metodą stożków niezmienniczych.
; mamy więc wyznaczoną wiązkę stabilną.
Wykazanie istnienia wiązki niestabilnej jest trudniejsze. Metoda opisana poniżej nazywana jest metodą stożków niezmienniczych.
Wykażemy najpierw że istnieje ”wiązka niezmiennicza stożków niestabilnych”.
W kazdym punkcie solenoidu ![]() rozważamy stożek (podzbiór przestrzeni stycznej zaczepionej w tym punkcie), opisany nierównością:
rozważamy stożek (podzbiór przestrzeni stycznej zaczepionej w tym punkcie), opisany nierównością:
(Zatem jest to rodzina stożków połozonych ”poziomo”).
Różniczka ![]() nie zachowuje kierunku poziomego, czyli wektora postaci
nie zachowuje kierunku poziomego, czyli wektora postaci ![]() (tak jest tylko dla
(tak jest tylko dla ![]() .
Ale- zachowuje rodzinę stożków poziomych
.
Ale- zachowuje rodzinę stożków poziomych
Ćwiczenie 8.3
Sprawdzić że dla każdego ![]() mamy
mamy
Widzimy teraz jak można próbować uzyskać szukaną foliację niestabilną: skoro ![]() , to róWnież
, to róWnież
![]() , itd i otrzymujemy zstępujący ciąg stożków:
, itd i otrzymujemy zstępujący ciąg stożków:
Jeśli wykażemy że przecięcie tego ciągu stożków, zaczepionych w punkcie ![]() jest jedną prostą (zawartą w
jest jedną prostą (zawartą w ![]() ) otrzymamy jednowymiarową niezmienniczą foliację. Jeśli dodatkowo sprawdzimy, że
) otrzymamy jednowymiarową niezmienniczą foliację. Jeśli dodatkowo sprawdzimy, że ![]() rozciąga wektory należace do prostych z tak wybranej foliacji- otrzymamy brakującą foliację niestabilną.
rozciąga wektory należace do prostych z tak wybranej foliacji- otrzymamy brakującą foliację niestabilną.
Najpierw sprawdzimy warunek rozciągania:
Na stożkach ![]() możemy użyc dowolnej normy równoważnej z normą euklidesową (czyli np z normą
możemy użyc dowolnej normy równoważnej z normą euklidesową (czyli np z normą ![]() ).
Ponieważ
).
Ponieważ ![]() , więc na stożkach
, więc na stożkach ![]() równoważną normą jest po prostu
równoważną normą jest po prostu ![]() .
Oczywiście, ta norma jest mnożona przez
.
Oczywiście, ta norma jest mnożona przez ![]() przy działaniu różniczki
przy działaniu różniczki ![]() .
Zatem warunek rozciągania został sprawdzony.
.
Zatem warunek rozciągania został sprawdzony.
Aby sprawdzić że przecięcie ![]() jest jedną prostą, zobaczymy jak zmniejsza (zwęża) się stożek
jest jedną prostą, zobaczymy jak zmniejsza (zwęża) się stożek ![]() po zastosowaniu operatora rózniczki
po zastosowaniu operatora rózniczki ![]() . Weźmy dwa wektory
. Weźmy dwa wektory ![]() . ”Nachylenia” tych wektorów to wartości
. ”Nachylenia” tych wektorów to wartości ![]() ,
, ![]() . Niech teraz
. Niech teraz ![]() ,
,
![]() . Z wzoru na różniczkę
. Z wzoru na różniczkę ![]() dostajemy od razu:
dostajemy od razu:
Zatem różnica między nachyleniami obrazów przy ![]() dwóch dowolnych wektorów należących do stożka maleje wykładniczo z
dwóch dowolnych wektorów należących do stożka maleje wykładniczo z ![]() . Wynika stąd oczywiście że przecięcie zstępującego ciągu stożków
. Wynika stąd oczywiście że przecięcie zstępującego ciągu stożków
składa się dokładnie z jednej prostej. Jest to szukana przez nas foliacja niestabilna ![]() .
.
8.2. Dyfeomorfizmy Anosowa
Zaczniemy od przykładu. Rozważmy automorfizm algebraiczny torusa ![]() określony wzorem:
określony wzorem:
| (8.1) |
Mówiąc precyzyjniej, przekształcenie ![]() najpierw jest określone wzorem 8.1 na płaszczyźnie.
Ponieważ
najpierw jest określone wzorem 8.1 na płaszczyźnie.
Ponieważ ![]() jest liniowe i przekształca punkty o współrzędnych całkowitych na punkty o współrzędnych całkowitych,
jest liniowe i przekształca punkty o współrzędnych całkowitych na punkty o współrzędnych całkowitych, ![]() indukuje gładkie przekształcenie torusa
indukuje gładkie przekształcenie torusa ![]() .
Zauważmy że
.
Zauważmy że ![]() jest odwracalne (ponieważ wyznacznik macierzy jest równy
jest odwracalne (ponieważ wyznacznik macierzy jest równy ![]() ); przekształcenie odwrotne jest indukowane przez przekształcenie liniowe płaszczyzny o macierzy:
); przekształcenie odwrotne jest indukowane przez przekształcenie liniowe płaszczyzny o macierzy:
Punkt ![]() jest punktem stałym hiperbolicznym. Wartości własne dla macierzy przekształcenia
jest punktem stałym hiperbolicznym. Wartości własne dla macierzy przekształcenia ![]() to
to ![]() i
i ![]() . Odpowiednie (wzajemnie prostopadłe) kierunki własne to
. Odpowiednie (wzajemnie prostopadłe) kierunki własne to
![]() ,
, ![]() .
Oznaczmy prostą wyznaczoną przez pierwsze równanie na płaszczyźnie przez
.
Oznaczmy prostą wyznaczoną przez pierwsze równanie na płaszczyźnie przez ![]() , drugą prostą przez
, drugą prostą przez ![]() . Wówczas
. Wówczas
![]() (ta prosta jest rozciągana przy działąniu
(ta prosta jest rozciągana przy działąniu ![]() ); podobnie
); podobnie ![]() (ta prosta jest ściągana przy działaniu
(ta prosta jest ściągana przy działaniu ![]() ).
).
Zauważmy dalej że jeśli ![]() jest dowolnym punktem płąszczyzny, to obrazem prostej afinicznej
jest dowolnym punktem płąszczyzny, to obrazem prostej afinicznej ![]() jest prosta afiniczna
jest prosta afiniczna ![]() ; podobnie dla
; podobnie dla ![]() .
Mamy więc w każdym punkcie płaszczyzny wyznaczony kierunek stabilny
.
Mamy więc w każdym punkcie płaszczyzny wyznaczony kierunek stabilny ![]() i niestabilny
i niestabilny ![]() . Mamy też globalne rozmaitości niestabilną
. Mamy też globalne rozmaitości niestabilną ![]() i stabilną
i stabilną ![]() .
Po zrzutowaniu na torus proste
.
Po zrzutowaniu na torus proste ![]() ,
, ![]() utworzą foliacje stabilną i niestabilną dla przekształcenia
utworzą foliacje stabilną i niestabilną dla przekształcenia ![]() .
Zrzutowane proste są gęsto nawiniętymi obmotkami na torusie.
.
Zrzutowane proste są gęsto nawiniętymi obmotkami na torusie.
Wniosek 8.3
Dla tego dyfeomorfizmu cała rozmaitość ![]() jest zbiorem hiperbolicznym.
jest zbiorem hiperbolicznym.
Stwierdzenie 8.5
Zdefiniowany powyżej dyfeomorfizm ![]() ma gęsty zbiór orbit okresowych.
ma gęsty zbiór orbit okresowych.
Dowód pozostawimy jako zadanie:
Ćwiczenie 8.4
Wykazać że jeśli ![]() jest hiperbolicznym automorfizmem torusa
jest hiperbolicznym automorfizmem torusa ![]() to punkt
to punkt ![]() jest okresowy wtedy i tylko wtedy
jest okresowy wtedy i tylko wtedy ![]() dla pewnego punktu
dla pewnego punktu ![]() o wymiernych współrzędnych.
o wymiernych współrzędnych.
Zauważmy że ten dyfeomorfizm jest bardzo różny od dyfeomorfizmów Morse'a- Smale'a, omawianych przez nas wcześniej. Dla tamtych dyfeomorfizmów zbiór punktów niebładzących składał się ze skończonej liczby hiperolicznych orbit okresowych. Dowód ich strukturalnej stabilności (przeprowadziliśmy dowód dla dyfeomorfizmów okręgu w wykładzie ??? rozpoczynał się od sprawdzenia że przy małym zaburzeniu wszystkie orbity zachowają się.
W tej nowej sytuacji mamy nieskończenie wiele hiperbolicznych orbit okresowych. Mimo to, przy małym zaburzeniu wszystkie te orbity zachowują się! Twierdzenie to ma daleko idące uogólnienia (stabilność dowolnych zbiorów hiperbolicznych). Najpierw podamy elegancki dowód (pochodzący od J. Mosera) dla automorfizmu algebraicznego torusa.
Twierdzenie 8.3
Hiperboliczny automorfizm torusa ![]() jest
jest ![]() strukturalnie stabilny.
strukturalnie stabilny.
Będziemy dla uproszczenia zakładali że mamy do czynienia z automorfizmem ![]() dwuwymiarowego torusa.
Jest on reprezentowany przez macierz przekształcenia liniowego
dwuwymiarowego torusa.
Jest on reprezentowany przez macierz przekształcenia liniowego ![]() na płaszczyźnie.
NIech
na płaszczyźnie.
NIech ![]() będzie dyfeomorfizmem torusa bliskim
będzie dyfeomorfizmem torusa bliskim ![]() w
w ![]() topologii.
Twierdzimy że wówczas istnieje dyfeomorfizm płaszczyzny
topologii.
Twierdzimy że wówczas istnieje dyfeomorfizm płaszczyzny ![]() , który jest
, który jest ![]() bliski
bliski ![]() , i taki że
, i taki że
![]() . Istotnie, mamy
. Istotnie, mamy ![]() . Zatem, jeśli
. Zatem, jeśli ![]() jest
jest ![]() bliskie
bliskie
![]() to dla każdego
to dla każdego ![]() istnieje dokładnie jeden punkt
istnieje dokładnie jeden punkt ![]() który jest
który jest
![]() bliski punktowi
bliski punktowi ![]() na płaszczyźnie. Kładziemy
na płaszczyźnie. Kładziemy ![]() .
. ![]() jest zatem dobrze
określone; jest gładkie ponieważ -lokalnie
jest zatem dobrze
określone; jest gładkie ponieważ -lokalnie ![]() zapisuje się jako
zapisuje się jako ![]() (
dla pewnej gałezi
(
dla pewnej gałezi ![]() ).
Zastosujemy do przekształcenia liniowego
).
Zastosujemy do przekształcenia liniowego ![]() i do dyfeomorfizmu
i do dyfeomorfizmu ![]() twierdzenie Grobmana- Hartmana.
Możemy je zastosować bo
twierdzenie Grobmana- Hartmana.
Możemy je zastosować bo
![]() jest
jest![]() małym zaburzeniem
małym zaburzeniem ![]() w całym
w całym ![]() . Zatem
. Zatem ![]() możemy zapisać jako
możemy zapisać jako ![]() gdzie
gdzie ![]() jest klasy
jest klasy ![]() i jest
i jest ![]() bliskie zera.
bliskie zera.
Wspomniane Twierdzenie gwarantuje istnienie homeomorfizmu
![]() , który jest sprzężeniem między
, który jest sprzężeniem między ![]() i
i ![]() :
:
| (8.2) |
Oczywiście, nie wynika stąd że homeomorfizm ![]() da się zrzutować do homeomorfizmu
da się zrzutować do homeomorfizmu ![]() na torusie, sprzęgającego działanie
na torusie, sprzęgającego działanie ![]() i
i ![]() . Przypomnijmy, że w dowodzie twierdzenia Grobmana- Hartmana (rozdział
. Przypomnijmy, że w dowodzie twierdzenia Grobmana- Hartmana (rozdział ![]() ) homeomorfizm
) homeomorfizm ![]() otrzymuje się w postaci
otrzymuje się w postaci ![]() (
(![]() jest przekształceniem identycznościowym).
Na to żeby
jest przekształceniem identycznościowym).
Na to żeby ![]() rzutowało się do
rzutowało się do ![]() potrzeba aby dla każdego
potrzeba aby dla każdego ![]() istniało
istniało ![]() takie że
takie że
czyli ![]() ,
, ![]() . Jeśli
. Jeśli ![]() ma być bliskie identyczności (czyli
ma być bliskie identyczności (czyli ![]() ma być małe) to trzeba aby
ma być małe) to trzeba aby ![]() , czyli żeby
, czyli żeby ![]() było (dwu)okresowe.
Wówczas
było (dwu)okresowe.
Wówczas ![]() jest dobrze określone i jest homeomorfizmem torusa.
Musimy zatem wykazać że w dowodzie twierdzenia Grobmana- Hartmana możemy poszukiwać rozwiązania zagadnienia 8.2
w postaci
jest dobrze określone i jest homeomorfizmem torusa.
Musimy zatem wykazać że w dowodzie twierdzenia Grobmana- Hartmana możemy poszukiwać rozwiązania zagadnienia 8.2
w postaci ![]() gdzie u należy do podprzestrzeni przestrzeni
gdzie u należy do podprzestrzeni przestrzeni ![]() złożonej z funkcji dwuokresowych.
Oznaczmy tę podprzestrzeń przez
złożonej z funkcji dwuokresowych.
Oznaczmy tę podprzestrzeń przez ![]() . Tak jak w dowodzie twierdzenia Grobmana- Hartmana, wprowadzamy operator
. Tak jak w dowodzie twierdzenia Grobmana- Hartmana, wprowadzamy operator
![]() działający w przestrzeni funkcji
działający w przestrzeni funkcji ![]() , określony wzorem
, określony wzorem ![]() . Tak samo jak poprzednio, stwierdzamy że
. Tak samo jak poprzednio, stwierdzamy że ![]() jest odwracalny, skoro
jest odwracalny, skoro ![]() jest hiperboliczny.
Zauważamy teraz że
jest hiperboliczny.
Zauważamy teraz że ![]() przekształca funkcję dwuokresową
przekształca funkcję dwuokresową ![]() na funkcję dwuokresową. Zatem
na funkcję dwuokresową. Zatem ![]() zachowuje przestrzeń
zachowuje przestrzeń ![]() .
Przekształcenie
.
Przekształcenie
jest kontrakcją w normie ![]() i zachowuje domkniętą podprzestrzeń
i zachowuje domkniętą podprzestrzeń ![]() . Zatem jedyny punkt stały
. Zatem jedyny punkt stały ![]() leży w podprzestrzeni
leży w podprzestrzeni ![]() .
.
Punkt stały ![]() spełnia równanie
spełnia równanie
czyli ![]() spełnia
spełnia
. Wówczas homeomorfizm ![]() rzutuje się do homeomorfizmu
rzutuje się do homeomorfizmu ![]() , czyli
, czyli
![]() i
i ![]() jest szukanym sprzężeniem:
jest szukanym sprzężeniem: ![]() .
.
Wniosek 8.4
Jest to jeszcze jeden sposób na przekonanie się że w wymiarze ![]() dyfeomorfizmy Morse'a-Smale'a na gładkiej zwartej rozmaitości nie stanowią gęstego podzioru w
dyfeomorfizmy Morse'a-Smale'a na gładkiej zwartej rozmaitości nie stanowią gęstego podzioru w ![]() topologii.
topologii.
8.3. Stabilność zbiorów hiperbolicznych
Stwierdzenie 8.6 (Zbió hiperboliczny dla bliskiego przekształcenia)
Niech ![]() będzie zbiorem hiperbolicznym dyfeomorfizmu
będzie zbiorem hiperbolicznym dyfeomorfizmu ![]() . Wówczas istnieje otoczenie
. Wówczas istnieje otoczenie ![]() zbioru
zbioru ![]() takie że jeśli
takie że jeśli ![]() jest dyfeomorfizmem, dostatecznie bliskim (w
jest dyfeomorfizmem, dostatecznie bliskim (w ![]() metryce)
metryce) ![]() na
na ![]() , to zbiór
, to zbiór
jest hiperboliczny.
Uwaga 8.4
Nie wiemy jeszcze jak zbiór ![]() jest związany z
jest związany z ![]() , a nawet- czy jest niepusty.
, a nawet- czy jest niepusty.
Na zbiorze ![]() mamy rozkład przestrzeni stycznej
mamy rozkład przestrzeni stycznej ![]() , zależny wsposób ciągły od
, zależny wsposób ciągły od ![]() . Możemy ten rozkład rozszerzyć do ciągłego (niekoniecznie niezmienniczego!) na pewne otoczenie
. Możemy ten rozkład rozszerzyć do ciągłego (niekoniecznie niezmienniczego!) na pewne otoczenie ![]() .
.
Rozpatrujemy teraz rodzinę stożków poziomych i pionowych. Stożki poziome to
stożki pionowe:
Jeśli ![]() , to stożek poziomy
, to stożek poziomy ![]() jest przekształcany przez
jest przekształcany przez ![]() w stożek poziomy zaczepiony w punkcie
w stożek poziomy zaczepiony w punkcie ![]() ; podobnie stożek pionowy
; podobnie stożek pionowy ![]() jest przekształcany przez
jest przekształcany przez ![]() w stożek pionowy w punkcie
w stożek pionowy w punkcie ![]() ; dokładniej- mamy nawet pewien ”zapas”- obraz
; dokładniej- mamy nawet pewien ”zapas”- obraz ![]() jest zawarty w
jest zawarty w ![]() ; podobnie dla stożków pionowych. Dzięki temu, jeśli
; podobnie dla stożków pionowych. Dzięki temu, jeśli ![]() jest bliskie
jest bliskie ![]() w
w ![]() metryce, to również
metryce, to również ![]() zachowuje tę rodzinę stożków poziomych i pionowych; nie tylko dla
zachowuje tę rodzinę stożków poziomych i pionowych; nie tylko dla ![]() ale też dla
ale też dla ![]() , gdzie
, gdzie ![]() jest pewnym otoczeniem
jest pewnym otoczeniem ![]() .
.
Wykażemy że stąd wynika dla punktów ![]() istnienie niezmienniczego rozkładu
istnienie niezmienniczego rozkładu ![]() na podprzestrzeń stabilną i niestabilną przy działaniu
na podprzestrzeń stabilną i niestabilną przy działaniu ![]() .
.
W tym celu udowodnimy następujący
Lemat 8.1
Niech ![]() będzie ciągiem przekształceń liniowych takich że
będzie ciągiem przekształceń liniowych takich że
-
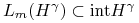
-
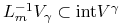
-
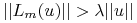 dla
dla 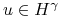
-
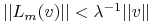 dla
dla 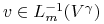 .
.
Wówczas zbiory
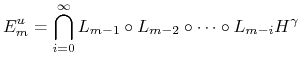 |
oraz
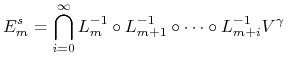 |
są (odpowiednio) ![]() - i
- i ![]() - wymiarowymi podprzestrzeniami liniowymi
- wymiarowymi podprzestrzeniami liniowymi ![]()
do skończenia
8.4. DA atraktor
do uzupełnienia
Naszkicujemy konstrukcję interesujacego atraktora, który powstaje dla przekształcenia uzyskanego przez modyfikację automorfizmu ergodycznego torusa (stąd nazwa: Derived from Anosov). Zaczynamy od opisanego w poprzednim rozdziale
hiperbolicznego automorfizmu torusa ![]() wyznaczonego przez przekształcenie liniowe
wyznaczonego przez przekształcenie liniowe
Punkt ![]() jest punktem stałym hiperbolicznym. Zmodyfikujemy przekształcenie w otoczeniu punktu
jest punktem stałym hiperbolicznym. Zmodyfikujemy przekształcenie w otoczeniu punktu ![]() tak aby stał się źródłem; blisko pojawią się dwa inne punkty stałe (siodła).
Ustalmy więc małe otoczenie
tak aby stał się źródłem; blisko pojawią się dwa inne punkty stałe (siodła).
Ustalmy więc małe otoczenie ![]() punktu
punktu ![]() ; będziemy w nim używali współrzędnych w bazie wyznaczonej przez kierunki własne. Zatem zapis wektora
; będziemy w nim używali współrzędnych w bazie wyznaczonej przez kierunki własne. Zatem zapis wektora ![]() oznacza że wektor ten jest kombinacją liniową
oznacza że wektor ten jest kombinacją liniową ![]() .
Zmodyfikujemy przekształcenie
.
Zmodyfikujemy przekształcenie ![]() ”likwidując” ściaganie w kierunku stabilnym.
Formalnie, można to zrobic na przykład tak:
Weźmy pomocniczą funkcję
”likwidując” ściaganie w kierunku stabilnym.
Formalnie, można to zrobic na przykład tak:
Weźmy pomocniczą funkcję ![]() klasy
klasy ![]() o wykresie w kształcie ”dzwonu”:
o wykresie w kształcie ”dzwonu”:
![]() dla
dla ![]() ,
, ![]() dla
dla ![]() . Rozpatrujemy w otoczeniu punktu
. Rozpatrujemy w otoczeniu punktu ![]() pole wektorowe o równaniu:
pole wektorowe o równaniu:
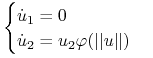 |
Oznaczając przez ![]() potok tego pola widzimy że
potok tego pola widzimy że
i że poza otoczeniem zera ![]()
![]() jest identycznością.
jest identycznością.
Nasze nowe przekształcenie to
gdzie ![]() jest na tyle duże że
jest na tyle duże że ![]() jest większe od odwrotności mniejszej wartości własnej
jest większe od odwrotności mniejszej wartości własnej ![]() .
We współrzędnych w bazie wektorów własnych
.
We współrzędnych w bazie wektorów własnych ![]() macierz różniczki
macierz różniczki ![]() ma postać
ma postać
Zatem punkt ![]() stał się źródłem.
Nowe przekształcenie też jest dyfeomorfizmem.
stał się źródłem.
Nowe przekształcenie też jest dyfeomorfizmem.
Wykażemy
Twierdzenie 8.4
Dla dyfeomorfizmu ![]() mamy:
mamy:
gdzie ![]() jest hiperbolicznym atraktorem. Wymiar topologiczny
jest hiperbolicznym atraktorem. Wymiar topologiczny ![]() jest równy
jest równy ![]() .
. ![]() jest topologicznie tranzytywne. Orbity okresowe są gęste w
jest topologicznie tranzytywne. Orbity okresowe są gęste w ![]()
Rozmaitość stabilna dla ![]() (jest to podprzestrzeń liniowa stabilna)
(jest to podprzestrzeń liniowa stabilna) ![]() jest zachowywana oczywiście również przez
jest zachowywana oczywiście również przez ![]() ; podobnie- podprzestrzeń niestabilna. Przekształcenie obcięte do rozmaitości niestabilnej pozostaje niezmienione.
Natomiast na rozmaitości stabilnej (rysunek)
pojawiają się dwa nowe punkty stałe
; podobnie- podprzestrzeń niestabilna. Przekształcenie obcięte do rozmaitości niestabilnej pozostaje niezmienione.
Natomiast na rozmaitości stabilnej (rysunek)
pojawiają się dwa nowe punkty stałe ![]() .
rysunek
.
rysunek
Twierdzimy że są to siodła.
Istotnie, w kierunku stabilnym różniczka ma wartość własną mniejszą niż ![]() .
Zauważmy że macierz różniczki dyfeomorfizmu
.
Zauważmy że macierz różniczki dyfeomorfizmu ![]() ma postać
ma postać
Wynika to stąd że potok ![]() zachowuje współrzędną
zachowuje współrzędną ![]() .
Zatem
.
Zatem ![]() ma postać
ma postać
Dla różniczki wyliczonej w punktach ![]() i
i ![]() wyraz zaznaczony
wyraz zaznaczony ![]() ma moduł mniejszy niż
ma moduł mniejszy niż ![]() (por. wykres przekształcenia
(por. wykres przekształcenia ![]() obciętego do podrzestrzeni stabilnej
obciętego do podrzestrzeni stabilnej ![]() .
Zatem
.
Zatem ![]() ,
, ![]() są siodłami.
są siodłami.
Z naszych rozważań wynika też że w całym zbiorze ![]() różniczka
różniczka ![]() ma postać
ma postać
Dla różniczki policzonej w punkcie ![]() oczywiście
oczywiście ![]() jest równe
jest równe ![]() , zaś
, zaś ![]() ma moduł większy od
ma moduł większy od ![]() .
.
Ustalmy teraz otoczenie ![]() ounktu
ounktu ![]() takie że
takie że
-
Dla
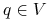 wyraz
wyraz 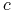 w wyrażeniu na różniczkę
w wyrażeniu na różniczkę 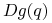 jest większy (co do modułu) od
jest większy (co do modułu) od 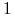 .
. -
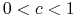 dla różniczki policzonej w punktach
dla różniczki policzonej w punktach 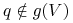 (czyli poza
(czyli poza 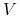
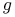 pozostaje ściągające wzdłuż wyjsciowego kierunku stabilnego
pozostaje ściągające wzdłuż wyjsciowego kierunku stabilnego 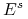 ).
). -
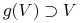
Istnienie takiego ![]() wynika z linearyzacji
wynika z linearyzacji ![]() w otoczeniu
w otoczeniu ![]() .
.
Skoro ![]() to
to ![]() ; ponadto
; ponadto ![]() .
Niech
.
Niech ![]() . Wówczas
. Wówczas ![]() .
.
Definiujemy ![]()
Widać jak powstaje zbiór ![]() . Operacja zamiany
. Operacja zamiany ![]() na
na ![]() prowadzi do ”rozszczepienia” rozmaitości stabilnej punktu
prowadzi do ”rozszczepienia” rozmaitości stabilnej punktu ![]() ; staje sie on źródłem, a dodatkowo powstają dwa siodła
; staje sie on źródłem, a dodatkowo powstają dwa siodła ![]() i
i ![]() . ”Szczelina” pomiędzy
. ”Szczelina” pomiędzy ![]() i
i ![]() to
to ![]() . Uzupełnienie tego zbioru to
. Uzupełnienie tego zbioru to ![]() .
.





