Zagadnienia
1. Układy dynamiczne- definicje i przykłady
1.1. Co to jest układ dynamiczny
-
Układ dynamiczny (topologiczny)
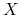 -przestrzeń topologiczna (najczęściej- metryczna),
-przestrzeń topologiczna (najczęściej- metryczna), 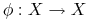 - przekształcenie ciągłe.
- przekształcenie ciągłe. -
Układ dynamiczny (metryczny)
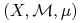 - przestrzeń z miarą probabilistyczną.
- przestrzeń z miarą probabilistyczną.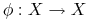 przekształcenie mierzalne zachowujące miarę
przekształcenie mierzalne zachowujące miarę 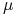 .
.Tu definicja:
Definicja 1.1
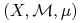 przestrzeń z miarą. Mówimy że przekształcenie
przestrzeń z miarą. Mówimy że przekształcenie 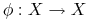 jest mierzalne
jeśli dla każdego
jest mierzalne
jeśli dla każdego 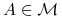 przeciwobraz
przeciwobraz 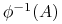 również należy do
również należy do 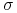 - ciała
- ciała 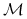 .
.Definicja 1.2
Przekształcenie mierzalne
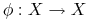 zachowuje miarę
zachowuje miarę 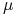 jeśli dla każdego
jeśli dla każdego 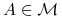
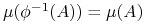 .
. -
Układ dynamiczny (gładki), z czasem dyskretnym
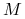 - gładka rozmaitość,
- gładka rozmaitość, 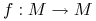 dyfeomorfizm (lub endomorfizm) klasy
dyfeomorfizm (lub endomorfizm) klasy 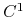
-
Układ dynamiczny (gładki) z czasem ciąglym
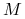 - gładka rozmaitość (na ogół zakłada się też zwartość),
- gładka rozmaitość (na ogół zakłada się też zwartość),
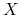 - pole wektorowe na
- pole wektorowe na 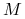 , klasy
, klasy 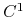 ,
, 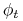 - potok pola wektorowego
- potok pola wektorowego 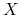 .
Jest to rodzina dyfeomorfizmów, tzn
.
Jest to rodzina dyfeomorfizmów, tzn 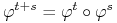
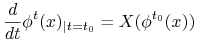
Jeśli rozmaitość jest zwarta to z twierdzenia o przedłużaniu trajektorii wynika że potok pola wektorowego
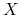 jest określony dla wszystkich
jest określony dla wszystkich 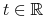 . Rodzina przekształceń
. Rodzina przekształceń 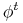 jest więc jednoparametrową grupą dyfeomorfizmów
jest więc jednoparametrową grupą dyfeomorfizmów 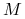 .
.
Definicja 1.3
Niech ![]() będzie układem dynamicznym z czasem dyskretnym. Trajektorią punktu
będzie układem dynamicznym z czasem dyskretnym. Trajektorią punktu ![]() nazywamy ciąg nieskończony
nazywamy ciąg nieskończony ![]() .
.
1.2. Najprostsze przykłady
Przykład 1.1 (Obrót na okręgu)
Niech ![]() ; określamy przekształacenie
; określamy przekształacenie
To przekształcenie zachowuje oczywiście miarę Lebesgue'a na okręgu.
Zauważmy że jeśli ![]() jest wymierne- każda trajektoria jest okresowa, a gdy
jest wymierne- każda trajektoria jest okresowa, a gdy ![]() jest niewymierne- każda trajektoria jest gęsta (dlaczego?).
jest niewymierne- każda trajektoria jest gęsta (dlaczego?).
Przykład 1.2 (Przesunięcie na torusie)
Torus możemy utożsamiać z przestrzenią ilorazową ![]() ; gdzie relacja utożsamienia jest następująca:
; gdzie relacja utożsamienia jest następująca:
Zatem - torus można też utożsamiać z produktem dwóch okręgów ![]() .
Na płaszczyźnie rozważamy przekształcenie
.
Na płaszczyźnie rozważamy przekształcenie ![]() . Wyznacza ono przekształcenie torusa
. Wyznacza ono przekształcenie torusa
gdzie
![]() .
.
Zauważmy że jeśli ![]() są pierwiastkami z jedynki (rówmoważnie- jeśli
są pierwiastkami z jedynki (rówmoważnie- jeśli ![]() są wymierne) to każda trajektoria jest okresowa.
są wymierne) to każda trajektoria jest okresowa.
Załóżmy że ![]() są niezależne nad pierścieniem
są niezależne nad pierścieniem ![]() , to znaczy
, to znaczy ![]() ma tylko jedno rozwiązanie w liczbach całkowitych:
ma tylko jedno rozwiązanie w liczbach całkowitych: ![]() . Poniżej sprawdzimy że wtedy
każda trajektoria jest gęsta w
. Poniżej sprawdzimy że wtedy
każda trajektoria jest gęsta w ![]() .
.
Natomiast jeśli ![]() są zależne nad
są zależne nad ![]() , ale przynajmniej jedna z tych liczb jest niewymierna, to mamy jeszcze inna sytuację (niewidoczną w przypadku jednowymiarowym): niech, np
, ale przynajmniej jedna z tych liczb jest niewymierna, to mamy jeszcze inna sytuację (niewidoczną w przypadku jednowymiarowym): niech, np ![]() . Wówczas torus jest sumą niezmienniczych okręgów; każda trajektoria jest gęsta na ”swoim” okręgu, ale żadna trajektoria nie jest gęsta na torusie.
. Wówczas torus jest sumą niezmienniczych okręgów; każda trajektoria jest gęsta na ”swoim” okręgu, ale żadna trajektoria nie jest gęsta na torusie.
W następnym rozdziale zbadamy ogólną sytuację przesunięcia na ![]() -wymiarowym torusie. Wprowadzimy tez ważne w Układach Dynamicznych pojęcie topologicznej tranzytywności.
-wymiarowym torusie. Wprowadzimy tez ważne w Układach Dynamicznych pojęcie topologicznej tranzytywności.
Przykład 1.3 (Układ z ciągłym czasem na torusie)
Określamy jednoparametrową grupę przekształceń torusa:
Te przekształcenia w ![]() przed utożsamieniem, mają postać
przed utożsamieniem, mają postać
Jest to więc potok pola wektorowego (równania różniczkowego) na płaszczyźnie:
Przykład 1.4 (Układ z ciągłym czasem na płaszczyźnie)
Ten układ we współrzędnych biegunowych ma postać
Zatem - dla każdego punktu ![]() , poza stacjonarnym punktem
, poza stacjonarnym punktem ![]() , zbiór punktów granicznych trajektorii jest okręgiem
, zbiór punktów granicznych trajektorii jest okręgiem ![]() , ten okrąg jest trajektorią zamkniętą.
, ten okrąg jest trajektorią zamkniętą.
Przykład 1.5 (Układ z ciągłym czasem na płaszczyźnie)
Jest to zaburzenie układu
Łatwo sprawdzić że dla tego drugiego układu funkcja ![]() jest całką pierwszą. Zatem - trajektorie są zawarte w poziomicach funkcji
jest całką pierwszą. Zatem - trajektorie są zawarte w poziomicach funkcji ![]() .
.
Ćwiczenie 1.1
Naszkicować poziomice ![]() . Następnie, badając znak pochodnej
. Następnie, badając znak pochodnej ![]() dla wyjściowego układu, naszkicować jego trajektorie. Zbadać punkty skupienia trajektorii.
dla wyjściowego układu, naszkicować jego trajektorie. Zbadać punkty skupienia trajektorii.
1.3. Topologiczna tranzytywność: przykład- przesunięcie na torusie
Definicja 1.4
Niech ![]() będzie przestrzenią metryczną zwartą,
będzie przestrzenią metryczną zwartą, ![]() - przekształceniem ciągłym. Mówimy że
- przekształceniem ciągłym. Mówimy że ![]() jest topologicznie tranzytywne jeśli dla dowolnych otwartych podzbiorów
jest topologicznie tranzytywne jeśli dla dowolnych otwartych podzbiorów ![]() istnieje
istnieje ![]() takie że
takie że
| (1.1) |
Wykażemy
Stwierdzenie 1.1
Niech ![]() będzie metryczną przestrzenią zwartą i ośrodkową. Niech
będzie metryczną przestrzenią zwartą i ośrodkową. Niech ![]() będzie przekształceniem ciągłym. Wówczas
będzie przekształceniem ciągłym. Wówczas ![]() jest topologicznie tranzytywne wtedy i tylko wtedy gdy istnieje
jest topologicznie tranzytywne wtedy i tylko wtedy gdy istnieje ![]() takie że trajektoria
takie że trajektoria ![]() jest gęsta w
jest gęsta w ![]() .
.
Jeśli istnieje gęsta trajektoria to istnieją ![]() takie że
takie że ![]() ,
, ![]() . Zatem
. Zatem ![]() .
Aby dowieść drugą implikację, ustalmy przeliczalną bazę topologii
.
Aby dowieść drugą implikację, ustalmy przeliczalną bazę topologii ![]() . Ustalamy jeden zbiór z tej rodziny
. Ustalamy jeden zbiór z tej rodziny ![]() . Rozpatrzmy teraz zbiór
. Rozpatrzmy teraz zbiór ![]() złożony z punktów, których trajektorie omijają
złożony z punktów, których trajektorie omijają ![]() :
:
Ten zbiór jest domknięty i brzegowy (ta druga własność wynika stąd że założyliśmy (1.1)).
Z Twierdzenia Baire'a (zauważmy że przestrzeń ![]() jest zupełna) wynika że zbiór
jest zupełna) wynika że zbiór
jest brzegowy, i -w szczególności- niepusty. Każdy punkt ![]() ma gęstą trajektorię.
ma gęstą trajektorię.
Zbadamy teraz topologiczną tranzytywność przesunięć na ![]() -wymiarowych torusach.
Oczywiście, przesunięcie na
-wymiarowych torusach.
Oczywiście, przesunięcie na ![]() jest dane wzorem
jest dane wzorem
| (1.2) |
Mamy
Stwierdzenie 1.2
Niech ![]() będzie przesunięciem na torusie
będzie przesunięciem na torusie ![]() . Wówczas
. Wówczas ![]() jest topologicznie tranzytywne wtedy i tylko wtedy gdy
jest topologicznie tranzytywne wtedy i tylko wtedy gdy ![]() są niezależne nad
są niezależne nad ![]() , tj. jeśli dla pewnych
, tj. jeśli dla pewnych ![]()
to ![]() .
.
Załóżmy że współrzedne przesunięcia ![]() są zależne;
są zależne; ![]() .
Rozważmy funkcję
.
Rozważmy funkcję
Wówczas ![]() (mówimy że funkcja
(mówimy że funkcja ![]() jest
jest ![]() - niezmiennicza).
Rozważmy
- niezmiennicza).
Rozważmy ![]() ; ta funkcja też jest
; ta funkcja też jest ![]() - niezmiennicza. Widzimy że dla pewnego
- niezmiennicza. Widzimy że dla pewnego ![]() zbiory
zbiory ![]() i
i ![]() są niepuste. Ponadto, są one otwarte i
są niepuste. Ponadto, są one otwarte i ![]() -niezmiennicze:
-niezmiennicze: ![]() ,
,
![]() . Przeczy to tranzytywności.
. Przeczy to tranzytywności.
Załóżmy teraz że ![]() nie jest tranzytywne, czyli dla pewnych otwartych
nie jest tranzytywne, czyli dla pewnych otwartych ![]() i dla wszystkich naturalnych
i dla wszystkich naturalnych ![]()
![]() . Biorąc
. Biorąc ![]() i
i ![]() widzimy że są to dwa otwarte, rozłączne,
widzimy że są to dwa otwarte, rozłączne, ![]() - niezmiennicze podzbiory.
- niezmiennicze podzbiory.
Rozważmy funkcję ![]() - czyli funkcję charakterystyczną
- czyli funkcję charakterystyczną ![]()
Chcemy użyć rozwinięcia Fouriera tej funkcji, dokładniej- mamy
Stwierdzenie 1.3
W przestrzeni ![]() mamy ortonormalną bazę daną przez funkcje postaci
mamy ortonormalną bazę daną przez funkcje postaci
![]() .
.
Korzystając z tego stwierdzenia, możemy napisać
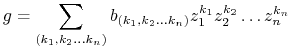 |
i rozkład ten jest jednoznaczny.
Wówczas
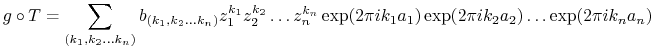 |
Z jednoznaczności rozwinięcia Fouriera wynika więc że
Ponieważ funkcja ![]() nie jest stała, jej rozwinięcie ma więcej niż jeden składnik. Wynika stąd że
dla pewnych
nie jest stała, jej rozwinięcie ma więcej niż jeden składnik. Wynika stąd że
dla pewnych ![]() (nie wszystkich równych zero) mamy
(nie wszystkich równych zero) mamy
Zauważmy jeszcze
Uwaga 1.1
Dla przesunęcia na torusie mamy równowżność: pewna trajektoria jest gęsta jest równoważne temu że każda trajektoria jest gęsta. Wynika to stąd że trajektorie dwóch różnych punktów różnią sie o przesunięcie (mnożenie przez element grupy ![]() )
)




