Zagadnienia

14.1 Entropia rozbicia
14.2 Entropia przekształcenia
14.3 Jak liczyć entropię metryczna

14. O entropii metrycznej

14.1. Entropia rozbicia

Niech $(X,\mathcal{F},\mu)$ będzie przestrzenią z miarą probabilistyczną.

Definicja 14.1

Rozbicie mierzalne $\xi=\{ A_{1},\dots,A_{k}\}$ - wszystkie $A_{i}$ są mierzalne, parami rozłączne i $\bigcup A_{i}=X$ .

Definicja 14.2

Niech $\xi,\eta$ będą rozbiciami. Określamy rozbicie (drobniejsze od obu)

$\xi\vee\eta$

Jest to rozbicie składające się ze wszystkich zbiorów postaci:

$A_{i}\cap B_{j},A_{i}\in\xi,B_{j}\in\eta.$

Definicja 14.3 (Entropia rozbicia)

Niech $\xi$ będzie rozbiciem mierzalnym, skończonym lub przeliczalnym.

$H(\xi)=\sum _{{a\in\xi}}-\mu(A)\log\mu(A)$

Ćwiczenie 14.1

Sprawdzić że, jeśli rozbicie $\xi$ ma $n$ elementów, to $H(\xi)\le\log n$ i równość zachodzi dla rozbicna na $n$ zbiorów o mierze $\frac{1}{n}$ każdy.

Definicja 14.4 (Entropia warunkowa)

Niech $\xi,\eta$ będą rozbiciami mierzalnymi, co najwyzej przeliczalnymi. Entropia $\xi$ pod warunkiem $\eta$ to

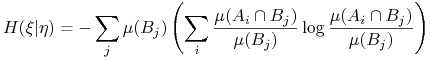$H(\xi|\eta)=-\sum _{j}\mu(B_{j})\left(\sum _{i}\frac{\mu(A_{i}\cap B_{j})}{\mu(B_{j})}\log\frac{\mu(A_{i}\cap B_{j})}{\mu(B_{j})}\right)$

Twierdzenie 14.1

Niech $\xi,\eta,\zeta$ będą rozbiciami Wówczas:

$H(\xi\vee\eta|\zeta)=H(\xi|\zeta)+H(\eta|\xi\vee\zeta)$
$H(\xi\vee\eta=H(\xi)+H(\eta|\xi)$
$\xi\le\eta\Rightarrow H(\xi|\zeta)\le H(\eta|\zeta)$
$\eta\le\zeta\Rightarrow H(\xi|\eta)\ge H(\xi|\zeta)$
$H(\xi\vee\eta|\zeta)\le H(\xi|\zeta)+H(\eta|\zeta)$
$H(\xi|\zeta)\le H(\xi|\eta)+H(\eta|\zeta)$

Dowód jest rachunkowy, zostawiony jako ćwiczenie

∎

14.2. Entropia przekształcenia

Niech $T:X\to X$ będzie przekształceniem zachowującym miarę $\mu$ .

Stwierdzenie 14.1 (Stwierdzenie i definicja entropii przekształcenia na rozbiciu)

Niech $\xi$ będzie rozbiciem co najwyżej przeliczalnym. Oznaczamy

$\xi _{0}^{n}=\xi\vee T^{{-1}}\xi\vee\dots\vee T^{{{}_{(}n-1)}}\xi.$

Wowczas istnieje granica

$\lim _{{n\to\infty}}\frac{1}{n}H(\xi _{0}^{n})$

nazywamy ją entropią $T$ względem rozbicia $\xi$ i oznaczamy $h(T,\xi)$

Wystarczy zauważyć że ciąg $H(\xi _{0}^{n})$ jest podaddytywny. Mamy

$H(\xi _{0}^{{n+m}})+H(\xi\vee T^{{-1}}\xi\vee\dots\vee T^{{{}_{(}n+m-1)}}\xi)=H\left((\xi\vee T^{{-1}}\xi\vee\dots\vee T^{{{}_{(}n-1)}}\xi)\vee(T^{{-n}}(\xi\vee\dots\vee t^{{-m}}\xi)\right)$

Z włąsności $(5)$ w poprzednim twierdzeniu i z niezmienniczości miary, możemy prawą stronę oszacować z góry przez

$H(\xi _{0}^{n})+H(\xi _{0}^{m})$

∎

Definicja 14.5 (Entropia przekształcenia)

Niech $T$ będzie przekształceniem zachowujacym miarę. Entropia $h_{\mu}(T)$ to

$h_{\mu}(T)=\sup _{{\xi}}h(T,\xi)$

gdzie supremum jest wziete po wszystkich skończonych mierzalnych rozbiciach $X$ .

Następujące ważne twierdzenie podajemy bez dowodu:

Twierdzenie 14.2 (Twierdzenie Shannona- Breimana- Mcmillana)

$(X,\mathcal{F},\mu)$ - przestrzeń z miarą probabilistyczną, $T$ - ergodyczne przekształcenie zachowujące miarę $\mu$ , $\xi$ - mierzalne rozbicie (skończone, albo przeliczalne, o skończonej entropii). Oznaczmy

$I(\xi _{0}^{{n-1}})(x)=-\log\mu(A_{n}(x)$

(gdzie $A_{n}(x)$ jest elementem rozbicia $\xi _{0}^{{n-1}}$ do którego należy punkt $x$ ). Wówczas:

$\frac{1}{n}I(\xi _{0}^{{n-1}})(x)\to H(t,\xi)$

prawie wszedzie i w $L^{1}(\mu)$ .

Bezpośrednio z definicji entropii wynika:

Twierdzenie 14.3

Entropia metryczna jest niezmiennikiem izomorfizmu miarowego przekształceń: jeśli $T$ zachowuje miarę $\mu$ na przestrzeni $X$ , zaś $S$ zachowuje miarę $\nu$ na przestrzeni $Y$ ,i istnieje mierzalna bijekcja $h:X\to Y$ przekształcająca miarę $\mu$ na miarę $\nu$ taka że $S\circ h=h\circ T$ , to $h_{\mu}(T)=h_{\nu}(S)$ .

14.3. Jak liczyć entropię metryczna

Widać że wyznaczenie entropii wymaga - według definicji- policzenia supremum po wszystkich skończonych rozbiciach. W wielu przypadkach można jednak wyliczyć entropię powołując się na twierdzenie poniżej:

Definicja 14.6

Niech $T$ będzie automorfizmem przestrzeni z miarą $(X,\mathcal{F},\mu)$ . Rozbicie $\xi$ nazywamy dwustronnym generatorem, jeśli najmniejsze $\sigma$ -ciało zawierajace wszystkie zbiory należące do rozbić $\bigvee _{{-N}}^{N}T^{n}\xi$ jest równe $\mathcal{F}$ .

Twierdzenie 14.4

Niech $T$ będzie automorfizmem przestrzeni z miarą $(X,\mathcal{F},\mu)$ . Założmy że $\xi$ jest dwustronnym generatorem. Wówczas

$h_{\mu}(T)=h_{\mu}(T,\xi).$

Przykład 14.1

Niech $T$ będzie obrotem na okręgu. Policzmymy entropię względem miary Lebesgue'a.

Jeśli kąt obrotu jest współmierny z $\pi$ , to $T^{k}={\rm Id}$ dla pewnego $k$ , a to oznacza że dla każdego skończonego rozbicia $\xi$ liczebność rozbicia $\xi\vee T^{{-1}}\xi\vee\dots\vee T^{{-n}}(\xi)$ jest ograniczona przez stała niezależna od $n$ . Zatem $H(\bigvee _{{i=1}}^{n}T^{{-i}}\xi)$ jest ograniczone, a stąd $h(t)=0$ .

Jeśli kąt obrotu nie jest współmierny z $\pi$ to rozbicie $\xi$ na dwa półokręgi jest dwustronnym generatorem (dlaczego); zatem- entropię można policzyć na tym rozbiciu.

Rozbicie $\bigvee _{0}^{{n-1}}T^{{-i}}\xi$ ma co najwyżej $2n$ elementów (dlaczego?) Stąd wynika że $\frac{1}{n}H(\bigvee _{0}^{{n-1}}T^{{-i}}\xi)\to 0$ .

Wykazaliśmy więc że entropia obrotu na okręgu, względem mairy Lebesgue'a, jest równa zero.

Przykład 14.2 (Przesunięcie Bernoulliego)

Niech $Y-\{ 0,2,\dots,k-1\}$ . Niech $X=\prod _{{-\infty}}^{\infty}Y$ . Elementami $X$ są więc nieskończone ciągi dwustronne, o wyrazach należących do zbioru $Y$ . W $Y$ wprowadzamy miarę, która każdemu elementowi $i$ przyporządkowyje wagę $p_{i}$ ; w $X$ wprowadzamy miarę produktową, an $\sigma$ -ciele generowanym przez wszystkie zbiory cylindryczne, postaci $x_{{-n}}=a_{{-n}},\dots,x_{0}=a_{0},\dots x_{n}=a_{n}$ . Przekształceniem $T$ jest przesunięcie ciągu w lewo o jedno miejsce. Oczywiście rozbicie $\xi$ na cylindry pierwszej generacji:

$x_{0}=a_{0}$

jest dwustronnym generatorem i można policzyć entropię na tym rozbiciu:

$\begin{aligned}\displaystyle h\mu(T)=&\displaystyle\lim\frac{1}{n}H(\xi\vee T^{{-1}}\xi\vee\dots\vee T^{{-(n-1)}}\xi)=-\lim\frac{1}{n}\sum _{{i_{0},i_{1},\dots i_{{n-1}}}}p_{{i_{0}}}p_{{i_{1}}}\dots p_{{i_{{n-1}}}}\log p_{{i_{0}}}p_{{i_{1}}}\dots p_{{i_{{n-1}}}}\\ \displaystyle&\displaystyle=-\lim\frac{1}{n}\sum _{{i_{0},\dots i_{{n-1}}=0}}^{{k-1}}p_{{i_{0}}}p_{{i_{1}}}\dots p_{{i_{{n-1}}}}(\log p_{{i_{0}}}+\log p_{{i_{1}}}+\dots+\log p_{{i_{{n-1}}}})\\ \displaystyle&\displaystyle=-\lim\frac{1}{n}n\left[p_{0}\log p_{0}(\sum _{{i_{1},\dots i_{{n-1}}}}p_{{i_{1}}}\dots p_{{i_{{n-1}}}})+p_{1}\log p_{1}(\sum _{{i_{0},i_{2}\dots i_{{n-1}}}}p_{{i_{0}}}p_{{i_{2}}}\dots p_{{i_{{n-1}}}})+\dots\right]\end{aligned}$

(14.1)

POnieważ każda z sum w nawiasach jest równa $1$ (dlaczego?), otrzymujemy

$h_{\mu}(T)=-\sum p_{i}\log p_{i}.$

Zatem- na przykład: przesunięcie Bernoulliego z wagami $\frac{1}{2},\frac{1}{2}$ i z wagami $\frac{1}{3}\frac{1}{3}\frac{1}{3}$ nie są izomorficzne, bo mają różne entropie.

Przesunięcia z wagami $\frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{4}$ i $\frac{1}{2},\frac{1}{8},\frac{1}{8},\frac{1}{8},\frac{1}{8}$ mają tę samą entropię, równą $2\log 2$ . W latach sześćdziesiątych Mieszałkin wykazał ze te dwa ostatnie układy są izomorficze (chociaż mają rózne liczby stanów). Późniejsze, słynne twierdzenie Ornsteina mówi, że dwa przesunięcia Bernoulliego są izomorficzne wtedy i tylko wtedy gdy mają równe entropie metryczne.

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Wstęp do teorii Układów Dynamicznych