Zagadnienia

2.1 Najprostszy układ- obrót na okręgu
2.2 Homeomorfizmy okręgu. Liczba obrotu
2.3 (Pół)sprzężenie z obrotem i Twierdzenie Denjoy

2. Układy dynamiczne na okręgu

2.1. Najprostszy układ- obrót na okręgu

Oznaczamy okrąg przez $S^{1}$ , zaś znormalizowaną miarę Lebesgue'a na $S^{1}$ przez $l$ . Oznaczmy przez $T_{\alpha}$ obrót na okręgu o kąt $2\pi\alpha$ . Równoważnie: rozpatrzmy na prostej $\mathbb{R}$ przekształcenie (przesunięcie o $\alpha$ ):

$F_{\alpha}(x)=x+\alpha.$

Przy naturalnym rzutowaniu $\pi:x\mapsto e^{{2\pi ix}}$ mamy

$T_{\alpha}\circ\pi=\pi\circ F_{\alpha}$

Dowód poniższego stwierdzenia pozostawiamy jako zadanie:

Stwierdzenie 2.1

(a) Jeśli 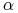$\alpha$ jest wymierne ( 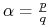$\alpha=\frac{p}{q}$ ), to każda trajektoria jest okresowa z okresem $q$ .
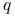(b) Jeśli 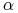$\alpha$ jest niewymierne, to każda trajektoria jest gęsta w $S^{1}$ .
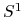(c)Jeśli 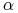$\alpha$ jest niewymierne to dla każdej funkcji ciągłej 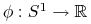$\phi:S^{1}\to\mathbb{R}$ mamy:

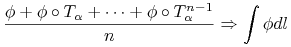
$\frac{\phi+\phi\circ T_{\alpha}+\dots+\phi\circ T^{{n-1}}_{\alpha}}{n}\Rightarrow\int\phi dl$
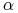(d) Jeśli $\alpha$ jest niewymierne to dla każdego 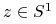$z\in S^{1}$ i dla każdego łuku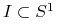 $I\subset S^{1}$

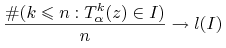
$\frac{\#(k\le n:T^{k}_{\alpha}(z)\in I)}{n}\to l(I)$

Uwaga 2.1

Z punktu (c) poprzedniego stwierdzenia mozemy wywnioskować że

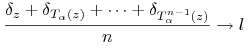$\frac{\delta _{z}+\delta _{{T_{\alpha}(z)}}+\dots+\delta _{{T^{{n-1}}_{\alpha}(z)}}}{n}\to l$

a nawet więcej: dla każdej miary borelowskiej probabilistycznej $\nu$ na $S^{1}$ i dla każdej funkcji ciągłej $\phi$ mamy:

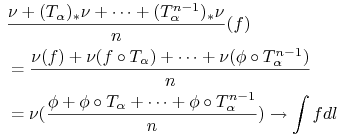$\begin{aligned}\displaystyle&\displaystyle\frac{\nu+(T_{\alpha})_{*}\nu+\dots+(T_{\alpha}^{{n-1}})_{*}\nu}{n}(f)\\ \displaystyle&\displaystyle=\frac{\nu(f)+\nu(f\circ T_{\alpha})+\dots+\nu(\phi\circ T_{\alpha}^{{n-1}})}{n}\\ \displaystyle&\displaystyle=\nu(\frac{\phi+\phi\circ T_{\alpha}+\dots+\phi\circ T_{\alpha}^{{n-1}}}{n})\to\int fdl\end{aligned}$

Użyta tutaj zbieżność miar to słaba-* zmieżność (inaczej- zbieżność według rozkładu).

Zatem ciąg miar

$\frac{\nu+(T_{\alpha})_{*}\nu+\dots+(T_{\alpha}^{{n-1}})_{*}\nu}{n}$

jest zbieżny słabo-* (inaczej: zbieżny według rozkładu) do znormalizowanej miary Lebesgue'a na $S^{1}$ .

Wynika stąd, że istnieje tylko jedna probabilistyczna borelowska miara niezmiennicza dla $T_{\alpha}$ - jest to miara Lebesgue'a.

2.2. Homeomorfizmy okręgu. Liczba obrotu

Niech $f$ będzie homeomorfizmem okręgu $S^{1}$ zachowującym orientację. Wówczas istnieje ściśle monotoniczna funkcja $F:\mathbb{R}\to\mathbb{R}$ taka że $\pi\circ F=f\circ\pi$ , gdzie $\pi$ jest naturalnym rzutowaniem $\pi:\mathbb{R}\to S^{1}$ . $\pi(x)=e^{{2\pi ix}}$ . Oczywiście funkcja $F$ (zwana podniesieniem $f$ ) nie jest wyznaczona jednoznacznie; wszystkie inne podniesienia są postaci $F(x)+k$ , gdzie $k\in\mathbb{Z}$ . Zauważmy własność podniesienia $F$ :

$F(x+1)=F(x)+1$

Oczywiście, podniesieniem obrotu $T_{\alpha}$ jest przekształcenie $F_{\alpha}$

Udowodnimy

Twierdzenie 2.1 (o istnieniu liczby obrotu)

Jeśli $f$ jest homeomorfizmem $S^{1}$ zachowującym orientację, $F$ jego dowolnym podniesieniem, to dla każdego $x\in\mathbb{R}$ istnieje granica

$\lim _{{n\to\infty}}\frac{F^{n}(x)}{n}=\rho(F)$

Ta granica nie zależy od punktu $x$ . Ponadto, jeśli $\tilde{F}=F+k$ jest innym podniesieniem, to $\rho(\tilde{F})=\rho(F)+k$ . Zatem część ułamkowa $\{\rho(F)\}$ nie zależy od podniesienia. Oznaczamy ją $\rho(f)$ i nazywamy liczbą obrotu homeomorfizmu $f$ .

Ponadto $\rho(f)\in\mathbb{Q}$ wtedy i tylko wtedy gdy $f$ ma punkt okresowy.

Załóżmy że $f$ ma punkt okresowy $x$ , $f^{q}(x)=x$ . Wybierzmy punkt $X\in\mathbb{R}$ leżący ”nad” $x$ , tzn taki że $\pi(X)=e^{{2\pi iX}}=x$ . Wówczas $F^{q}(X)=X+p$ dla pewnego $p\in\mathbb{Z}$ . Zatem

$F^{{2q}}(X)=F^{q}(F^{q}(X))=F^{q}(X+p)=F^{q}(X)+p=X+2p$

i przez indukcję:

$F^{{kq}}(X)=X+kp$

Dla $n\in\mathbb{N}$ znajdujemy $k$ takie że $kq\le n<(k+1)q$ i zapisujemy

$\frac{F^{n}(X)}{n}=\frac{F^{{n-kq}}(F^{{qk}}(X)}{n}=\frac{F^{{qk}}(X)}{n}+\frac{F^{{n-qk}}F^{{qk}}(X)-F^{{qk}}(X)}{n}$

Teraz widzimy że pierwszy składnik dąży do $\frac{p}{q}$ gdy $n\to\infty$ zaś drugi dąży do zera (wystarczy zauważyc że licznik jest ograniczony).

Założmy teraz że granica $\frac{F^{n}(X)}{n}$ istnieje Jeśli wybierzemy inny punkt $Y\in\mathbb{R}$ , to $Y\in[X+k,X+k+1)$ dla pewnego $k\in\mathbb{Z}$ . Możemy zatem zapisac:

$F^{n}(X)+k+1=F^{n}(X+k+1)>F^{n}(Y)\ge F^{n}(X+k)=F^{n}(X)+k$

Po podzieleniu przez $n$ widzimy że granica $\frac{F^{n}(Y)}{n}$ istnieje i jest taka sama jak dla punktu $X$ .

Załóżmy że $f$ nie ma punktu okresowego. Ustalamy $X$ , $m\in\mathbb{Z}$ . Wówczas $X+k<F^{m}(X)<X+k+1$ dla pewnego $k\in\mathbb{Z}$ . Stosując tę obserwację ponownie, mamy:

$X+2k<F^{m}(X)+k<F^{{2m}}(X)<F^{m}(X)+k+1<X+2(k+1)$

i, przez indukcję:

$X+nk<F^{{nm}}(X)<X+n(k+1),$

czyli

$nk=F^{{nm}}(X)-X<n(k+1).$

Oznaczając $a_{n}=\frac{F^{n}(X)-X}{n}$ mamy:

$\frac{k}{m}<a_{{nm}}<\frac{k+1}{m}$

oraz (kładąc $n=1$ )

$\frac{k}{m}<a_{{m}}<\frac{k+1}{m}$

Zatem $|a_{{nm}}-a_{m}|<\frac{2}{m}$ i podobnie (zamieniając $m$ i $n$ rolami) $|a_{{nm}}-a_{n}|<\frac{2}{n}$ . Stąd

$|a_{n}-a_{m}|<\frac{2}{m}+\frac{2}{n}$

Widzimy że ciąg $a_{n}$ spełnia warunek Cauchy'ego, zatem jest zbieżny.

Pozostaje do pokazania że jeśli $f$ nie ma punktu okresowego to $\rho(f)$ nie jest liczbą wymierną. Niech $\alpha=\frac{p}{q}$ ; pokażemy że $\alpha\neq\rho(f)$ . Zauważmy że $F^{q}(X)-X-p\neq 0$ dla każdego $X$ . Ponieważ funkcja $F^{q}(X)-X-p$ jest okresowa, wynika stąd że $|F^{q}(X)-X-p|>\delta$ dla pewnego dodatniego $\delta$ . Możemy założyc że $F^{q}(X)-X-p>\delta$ . Mamy wówczas (przez indukcję) $F^{{kq}}(X)-pk>k\delta$ a stąd:

$\lim _{{n\to\infty}}\frac{F^{n}(X)}{n}=\lim _{{k\to\infty}}\frac{F^{{kq}}(X)}{kq}>\frac{p}{q}+\frac{\delta}{q}$

∎

Uwaga 2.2

Dla liczby obrotu homeomorfizmy nie zachowujące orientacji nie są ciekawe. Sprawdzić że homeomorfizm zmieniający orientację ma dwa punkty stałe na okręgu i zerową liczbę obrotu.

2.3. (Pół)sprzężenie z obrotem i Twierdzenie Denjoy

Dla $x\in\mathbb{S}^{1}$ oznaczmy przez $\omega(x)$ zbiór punktów skupienia trajektorii w przód punktu $x$ . Udowodnimy najpierw

Stwierdzenie 2.2

Niech $f$ będzie homeomorfizmem okręgu zachowującym orientację, $\rho(f)\notin\mathbb{Q}$ . Wówczas albo

dla każdego $x\in S^{1}$ $\omega(x)=S^{1}$ albo
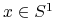
dla każdego 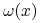$x\in S^{1}$ $\omega(x)$ jest (tym samym dla wszystkich 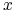$x$ !) zbiorem doskonałym, nigdziegęstym.

Dowód oprzemy na następującym łatwym lemacie:

Lemat 2.1

Niech $f$ będzie homeomorfizmem okręgu, $\rho(f)\notin\mathbb{Q}$ . Niech $m,n\in\mathbb{Z}$ , $x\in\mathbb{S}^{1}$ , $I$ - odcinek o końcach $f^{m}(x),f^{n}(x)$ . Wówczas dla każdego $y\in S^{1}$ orbita $y,f(y),\dots$ przecina $I$ .

Załóżmy że $m<n$ . Zauważmy że $f^{{m-n}}(I)$ jest odcinkiem przylegającym do $I$ , $f^{{2(m-n)}}I$ przylega do $f^{{m-n}}(I)$ itd. Otrzymujemy więc ciąg odcinków zawartych w $\omega(x)$ z ktorych następny przylega do poprzedniego. Twierdzimy że te odcinki pokryją cały okrąg. Istotnie, gdyby tak nie było- końce odcinków zbiegałyby do pewnego punktu $z\in\mathbb{S}^{1}$ , stałego dla $f^{{m-n}}$ , więc okresowego dla $f$ . Ale $f$ nie ma punktów okresowych.

Skoro tak określone odcinki pokrywają cały okrąg- istnieje $k\ge 0$ takie że $y\in f^{{k(m-n)}}(I)$ . Wtedy $f^{{k(n-m)}}(y)\in I$ .

∎

Z lematu natychmiast wynika że zbiór $\omega(x)$ nie zależy od $x$ . Istotnie, niech $p\in\omega(x)$ i niech $f^{{n_{i}}}(x)$ będzie ciągiem obrazów $x$ zbieżnym do $p$ . Weżmy dowolne $y\in\mathbb{S}^{1}$ . Wówczas między każdymi dwoma punktami $f^{{n_{i}}}(x),f^{{n_{{i+1}}}}$ znajdzie się jakis punkt z trajektorii $y$ , a zatem - istnieje ciąg obrazów $y$ zbieżny do $p$ .

Załóżmy teraz że $\omega(x)$ ma niepuste wnętrze. Wówczas istnieje odcinek $I\subset\omega(x)$ o końcach $f^{n}(x),f^{m}(x)$ (gdzie $m,n\in\mathbb{Z}$ . Wtedy $f^{{m-n}}(I)$ jest odcinkiem przylegającym do $I$ , $f^{{2(m-n)}}I$ przylega do $f^{{m-n}}(I)$ itd. Otrzymujemy więc ciąg odcinków zawartych w $\omega(x)$ z ktorych następny przylega do poprzedniego. Tak jak w dowodzie lematu - sprawdzamy że odcinki te muszą pokryć cały okrąg. Zatem $\omega(x)=\mathbb{S}^{1}$ .

Pozostaje do wykazania że zbiór $\omega(x)$ jest doskonały. Domkniętość wynika z samej definicji $\omega(x)$ . Niech $p\in\omega(x)$ . Wiemy już że zbiór graniczny $\omega(x)$ nie zależy od $x$ , w takim razie $\omega(x)=\omega(p)$ i $p\in\omega(p)$ . Zatem- istnieje ciąg $f^{{n_{i}}}(p)\to p$ . Wszystkie punkty $f^{{n_{i}}}(p)$ należą do $\omega(p)=\omega(x)$ . Więc $p$ jest granicą ciągu punktów należących do $\omega(x)$ . Wykazaliśmy że $\omega(x)$ jest doskonały.

∎

Twierdzenie 2.2 (o półsprzężeniu z obrotem)

Niech $f:\mathbb{S}^{1}\to\mathbb{S}^{1}$ będzie homeomorfizmem zachowującym orientację i $\alpha=\rho(f)$ niewymierne. Wówczas istnieje ciągłe i zachowujące orientację przekształcenie $h:\mathbb{S}^{1}\to\mathbb{S}^{1}$ stopnia $1$ takie że

$h\circ f=T_{\alpha}\circ h$

Ponadto, $h$ jest homeomorfizmem wtedy i tylko wtedy gdy $P(f)=\mathbb{S}^{1}$ .

Uwaga 2.3

Inaczej możemy wyrazić własności $h$ następująco: Jeśli $H:\mathbb{R}\to\mathbb{R}$ jest podniesieniem $h$ to $H(x+1)=H(x)+1$ i $H$ jest monotoniczne (chociaż niekoniecznie ścisle monotoniczne). W istocie przekonamy się że jeśli zbiór $P(f)$ nie jest całym okręgiem (wówczas - jak już wiemy- $\mathbb{S}^{1}\setminus P(f)$ jest otwarty i gęsty w $\mathbb{S}^{1}$ ) to funkcja $h$ przekształca każdą składową spójną zbioru $\mathbb{S}^{1}\setminus P(f)$ w jeden punkt.

Dowód twierdzenia o półsprzężeniu.

Wybieramy jakieś podniesienie $F$ homeomorfizmu $f$ . Wybieramy jakiś punkt $x\in P(f)$ i jego podniesienie $X\in\mathbb{R}$ . Rozpatrujemy zbiór $O_{X}=\{ F^{n}(X)+m\}$ (jest to dokładnie- podniesienie orbity $\{ f^{n}(x)\}$ do prostej przy kanonicznym rzutowaniu $\pi$ ). Określamy przekształcenie

$H:O_{X}\to\mathbb{R}$ wzorem:

$F^{n}(X)+m\mapsto n\alpha+m.$

Zauważmy następujące własności tego przekształcenia (zostawiamy sprawdzenie jako ćwiczenie):

Stwierdzenie 2.3

Przekształcenie $H$ zachowuje porządek, tzn.

$F^{{n_{1}}}(X)+m_{1}>F^{{n_{2}}}(X)+m_{2}\iff n_{1}\alpha+m_{1}>n_{2}\alpha+m_{2}.$

Ponadto

$H\circ F(Y)=H(Y)+\alpha,~~H(Y+1)=H(Y)+1,$

(2.1)

dla $Y\in O_{X}$ .

Przekształcenie $H$ można teraz przedłużyc do ciągłego na $\overline{O_{X}}=\pi^{{-1}}(P(f))$ . Istotnie, dla $x\in\overline{O_{X}}$ kładziemy:

$H(x)=\sup _{{y\in O_{X},y<x}}H(y)=\inf _{{y\in O_{X},y>x}}H(y).$

Te dwie wartości (sup i inf) pokrywają się. Wynika to stąd że $H$ jest ściśle rosnące na $O_{X}$ i że obraz $H(O_{X})=\{ n\alpha+m\}$ jest gęsty w $\mathbb{R}$ . Widzimy też (z określenia $H$ na domknięciu $O_{X}$ ) że jeśli $I$ jest składową uzupełnienia $O_{X}$ to $H_{{|I}}$ jest stała.

Rozszerzona funkcja $H$ ma oczywiście też własności opisane w równaniu (2.1). Ponieważ $H$ ma własność $H(x+1)=H(X)+1$ , $H$ wyznacza ciągłe przekształcenie $h:\mathbb{S}^{1}\to\mathbb{S}^{1}$ Z własności (2.1) wynika że $h\circ f=T_{\alpha}\circ h$ .

∎

Wykażemy teraz że przy pewnych założeniach na gładkość $f$ $h$ jest homeomorfizmem.

Dowód poprzedzimy spostrzeżeniem:

Stwierdzenie 2.4

Jeśli $f$ jest homeomorfizmem z niewymierną liczbą obrotu, $P(f)\neq\mathbb{S}^{1}$ , $I$ - składowa $\mathbb{S}^{1}\setminus P(f)$ , to $I$ jest zbiorem (łukiem) bładzącym:

$f^{n}(I)\cap f^{m}(I)=\emptyset$

dla $n,m\in\mathbb{Z}$ , $n\neq m$ .

Wystarczy zauważyć że jeśli $a,b$ są końcami $I$ to $f^{n}(I)$ jest łukiem o końcach $f^{n}(a),f^{n}(b)$ . Z niezmienniczości zbioru $P(f)$ wynika że punkty $a,b,f^{n}(a),f^{n}(b)\in P(f)$ i że $f^{n}(I)$ jest inną składową $\mathbb{S}^{1}\setminus P(f)$ .

∎

Wniosek 2.1

Przekształcenie $h$ skonstruowane w Twierdzeniu 6.1 jest homeomorfizmem wtedy i tylko wtedy gdy $f$ nie ma odcinka (łuku) bładzącego.

Twierdzenie 2.3 (Twierdzenie Denjoy)

Jeśli $f:\mathbb{S}^{1}\to\mathbb{S}^{1}$ jest dyfeomorfizmem klasy $C^{2}$ o niewymiernej liczbie obrotu, to $f$ jest topologicznie sprzężone z obrotem o kąt $\alpha=\rho(f)$ .

Uwaga 2.4

Oczywiście dla wymiernej liczby obrotu twierdzenie jest nieprawdziwe. Dla obrotu o kąt wymierny wszystkie punkty są okresowe.

Dowód Twierdzenia Denjoy

Zgodnie z poprzednim stwierdzeniem, wystarczy pokazać że $f$ nie ma odcinka (łuku) błądzącego. Niech $I$ będzie takim odcinkiem. Mamy wówczas

$|f^{n}(I)=|(f^{{\prime}})(z_{1}^{n})||I|,|f^{{-n}}(I)=|I|\cdot\frac{1}{|(f^{n})^{{\prime}}(z_{2}^{n})|}$

dla pewnych punktów $z_{1}^{n}\in I$ , $Z_{2}^{n}\in f^{{-n}}(I)$ . Mnożąc stronami otrzymujemy:

$\frac{|f^{n}(I)|\cdot|f^{{-n}}(I)|}{|I|}=|(f^{n})^{{\prime}}(z_{1}^{n})|\cdot\frac{1}{|(f^{n})^{{\prime}}(z_{2}^{n})|}$

Logarytmując mamy:

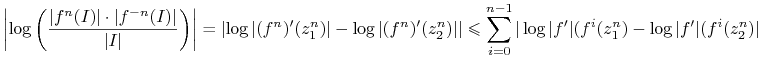$\left|\log\left(\frac{|f^{n}(I)|\cdot|f^{{-n}}(I)|}{|I|}\right)\right|=\left|\log|(f^{n})^{{\prime}}(z_{1}^{n})|-\log|(f^{n})^{{\prime}}(z_{2}^{n})|\right|\le\sum _{{i=0}}^{{n-1}}|\log|f^{{\prime}}|(f^{i}(z_{1}^{n})-\log|f^{{\prime}}|(f^{i}(z_{2}^{n})|$

Ponieważ $f$ jest dyfeomorfizmem klasy $C^{2}$ - funkcja $\log|f^{{\prime}}|$ jest lipschitzowska. Zatem ostatnią sume możemy oszacować z góry przez

$L\cdot\sum|[f^{i}(z_{1}^{n}),f^{i}(z_{2}^{n})]|$

gdzie $L=\sup\frac{f^{{\prime\prime}}}{f^{{\prime}}}$ jest stałą Lipschitza dla funkcji $\log|f^{{\prime}}|$ , zaś przez $[f^{i}(z_{1}^{n}),f^{i}(z_{2}^{n})]$ oznaczyliśmy odcinek (łuk) o końcach $f^{i}(z_{1}^{n})$ , $f^{i}(z_{2}^{n})$ .

Zauważmy teraz że wyrażenie po lewej stronie nierówności dąży do nieskończoności gdy $n\to\infty$ (wynika to stąd że długości odcinków $f^{n}(I),f^{{-n}}(I)$ muszą dążyć do zera, skoro jest to odcinek błądzący). Zatem, jeśli wskażemy nieskończony ciąg $n$ -ów, dla którego odcinki $[f^{i}(z_{1}^{n}),f^{i}(z_{2}^{n})]$ ( $i<n$ ) będą parami rozłaczne- dostaniemy sprzeczność , bo wówczas wyrażenie po prawej stronie będzie sie szacowało z góry przez długość okręgu.

Taki ciąg $n$ ów jest wskazany w następnym stwierdzeniu (ktore kończy dowód tw Denjoy)

Stwierdzenie 2.5

Niech $I$ będzie odcinkiem błądzącym dla $f$ , $V_{n}$ -minimalnym łukiem zawierającym $I,f^{{-n}}(I)$ , ale nie zawierajacym $f(I)$ . Wówczas dla nieskończenie wielu $n$ odcinki $V_{n},f(V_{n})\dots f^{{n-1}}(V_{n})$ są parami rozlączne.

Ze względu na półsprzężenie $f$ z obrotem o kąt $\alpha$ wystarczy udowodnić że dla nieskończenie wielu $n$ odcinek (łuk) $W_{n}$ łaczący punkty $x$ i $T_{\alpha}^{{-n}}(x)$ ma analogiczną własność: $W_{n},T^{\alpha}(W_{n})\dots T^{{n-1}}_{\alpha}(W_{n})$ są parami rozlączne. Można łatwo się przekonać że tak jest jeśli wybieramy $n$ jako czas ”najbliższego podejścia do początku trajektorii”, tzn takie $n$ że $d(x,T^{j}(x))>d(x,T^{n}(x))$ dla wszystkich $j=1,2,\dots n-1$ .

∎

Wniosek 2.2

Dla tak wybranych $n$ (łuki) $[f^{i}(z_{1}^{n}),f^{i}(z_{2}^{n})]$ ( $i=0,\dots,n-1$ ) są parami rozłączne, bo $[f^{i}(z_{1}^{n}),f^{i}(z_{2}^{n})]\subset f^{i}(V_{n})$ .

∎

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Wstęp do teorii Układów Dynamicznych