Zagadnienia

4.1 O poszukiwaniu punktów okresowych dla przekształceń odcinka
4.2 Twierdzenie Szarkowskiego
4.3 Bifurkacja podwajania okresu. Obserwacja Feigenbauma

4. Przekształcenia odcinka. Chaos na odcinku

4.1. O poszukiwaniu punktów okresowych dla przekształceń odcinka

Rozpatrzmy ciągłe przekształcenie $f:I\to I$ gdzie $I$ jest odcinkiem domkniętym.

Mówimy że odcinek (domknięty) $J\subset I$ nakrywa odcinek domknięty $K$ jeśli $K\subset f(J)$ . Oznaczenie: $J\longrightarrow K$ .

Lemat 4.1

Niech $J,K\subset I$ będą odcinkami. Załóżmy że $J\longrightarrow K$ . Wówczas istnieje domknięty odcinek $L\subset J$ taki że $f(L)=K$ .

Oznaczmy odcinek $K$ przez $[a,b]$ . Weźmy $c=\max\{ x\in J:f(x)=a\}$ , $d=\min\{ y>c:f(x)=b\}$ . Jeśli takie $d$ istnieje, odcinek $[c,d]$ jest szukanynm odcinkiem $L$ . Jeśli takie $d$ nie istnieje (wartośc $b$ nie jest przyjmowana na prawo od $c$ ),to istnieje $d<c$ takie że $f(x)=b$ . Wybieramy największe $d$ o takiej własności. Jesli wartość $a$ nie jest przyjmowana w odcinku $[d,c]$ , to jest to nasz szukany odcinek $L$ . W przeciwnym razie- modyfikujemy (zmniejszamy) $c$ , zastępując je najmniejszym $x>d$ takim że $f(x)=a$ .

∎

Lemat 4.2

Jeśli $J\longrightarrow J$ to $f$ ma punkt stały w $J$ .

Korzystamy z poprzedniego lematu. Mamy odcinek $L=[c,d]$ taki że $f(c)=a<c$ , $f(b)=d>b$ . Zatem funkcja $f(x)-x$ zmienia znak w odcinku $[c,d]$ , a stąd- istnieje punkt $e\in(c,d)$ taki że $f(e)=e$

∎

Przez prostą indukcję dostajemy następujące uogólnienie Lematu 4.1

Lemat 4.3

Jeśli

$I_{0}\longrightarrow I_{1}\longrightarrow I_{2}\longrightarrow\dots\longrightarrow I_{n}$

to w odcinku $I_{0}$ można znaleźć odcinek $L_{n}$ taki że $f^{n}(L_{n})=I_{n}$ .

Znajdujemy odcinek $L_{1}\subset I_{0}$ taki że $f(L_{1})=I_{1}$ . Ponieważ $I_{1}\longrightarrow I_{2}$ więc istnieje odcinek $L_{1}^{{\prime}}\subset I_{1}$ taki że $f(L_{1}^{{\prime}})=I_{2}$ . Zatem $L_{1}\longrightarrow L_{1}^{{\prime}}$ i istnieje odcinek $L_{2}\subset L_{1}$ taki że $f(L_{2})=L_{1}^{{\prime}}$ , czyli $f^{2}(L_{2})=I_{2}$ . Dalej postępujemy przez indukcje: mamy już $L_{k}\subset I_{0}$ takie że $f(L_{k})=I_{k}$ ; skoro $I_{k}\longrightarrow I_{{k+1}}$ to istnieje $L_{k}^{{\prime}}\subset I_{k}$ takie że $f(L_{k}^{{\prime}})=I_{{k+1}}$ . Wówczas $L_{k}\longrightarrow L_{k}^{{\prime}}$ (przy $f^{k}$ ) więc istnieje $L_{{k+1}}\subset L_{k}$ takie że $f^{k}(L_{{k+1}})=L_{k}^{{\prime}}$ , czyli $f^{{k+1}}(L_{{k+1}})=I_{{k+1}}$ .

∎

Wniosek 4.1

Jeśli

$I_{0}\longrightarrow I_{1}\longrightarrow I_{2}\dots\longrightarrow I_{{n-1}}\longrightarrow I_{0}$

to istnieje punkt okresowy $x$ o okresie $n$ taki że $x\in I_{0},f(x)\in I_{1}\dots f^{{n-1}}(x)\in I_{{n-1}}$ .

Ostatni wniosek służy do ”produkowania” orbit okresowych o zadanej trajektorii.

Udowodnimy następujące twierdzenie, pochodzące od Li i Yorka.

Twierdzenie 4.1 (”Okres 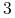$3$ implikuje chaos”)

Załóżmy że $f:I\to I$ ciągła i że $f$ ma punkt o okresie $3$ . Wówczas $f$ ma punkty okresowe o wszystkich okresach.

Oznaczmy orbitę o okresie $3$ przez $z_{1}<z_{2}<z_{3}$ . Załóżmy że $f(z_{2})=z_{3}$ . Oznaczmy $I_{1}=[z_{1},z_{2}],I_{2}=[z_{2},z_{3}]$ . Wówczas, skoro $z_{1}\mapsto z_{2}\mapsto z_{3}$ , mamy $I_{1}\longrightarrow I_{2},I_{2}\longrightarrow I_{1},I_{2}\longrightarrow I_{2}$ . Zatem możemy z naszym przekształceniem związać graf o dwóch wierzchołkach $(1),(2)$ i strzałkach $(1)\to(2),(2)\to 1,(2)\to(2)$ . Po pierwsze, zauważmy że skoro $(2)\to(2)$ , to z wniosku powyżej wynika że $f$ ma punkt stały zawarty w odcinku $I_{2}$ .

Każdej pętli w grafie odpowiada jakiś punkt okresowy. Rozważmy więc pętlę $(1)\to(2)\to(2)\to\dots\to(1)$ . Z wniosku 4.1 wynika że istnieje orbita okresowa $x_{0},x_{1},\dots x_{n}=x_{0}$ taka że $x_{0}\in I_{1}$ , $x_{i}\in I_{2}$ dla $i=1,\dots,n-1$ . Sprawdzimy że $n$ jest okresem podstawowym dla $x_{0}$ . Jeśli $x_{0}=x_{j}$ dla pewnego $j<n$ , to (biorąc pod uwagę że jeden z tych punktów leży w $I_{1}$ a drugi w $I_{2}$ ), $x_{0}$ musi być wspólnym końcem odcinków $I_{1}$ i $I_{2}$ , $x_{0}=z_{2}$ . To jednak jest niemożliwe. Istotnie, jeśli $n=2$ to $f^{2}(x_{0})=x_{0}$ podczas gdy $f^{2}(z_{2})\neq z_{2}$ . Jeśli zaś $n\ge 3$ to sprzeczność wynika z faktu że $f^{2}(z_{2})=z_{1}\in I_{1}$ , podczas gdy $f^{2}(x_{0})\in I_{2}$ .

∎

4.2. Twierdzenie Szarkowskiego

W latach sześćdziesiątych ukraiński matematyk Szarkowski wykazał że istnieje pewien niestandardowy porządek liniowy w zbiorze liczb naturalnych, ”rządzacy” pojawianiem się punktów okresowych dla funkcji ciągłych określonych na odcinku.

Zaczniemy od wprowadzenia tego porządku.

Definicja 4.1

Porządek Szarkowskiego:

Najpierw liczby nieparzyste większe niż $1$ ustawiamy w porządku malejącym:

$3>_{s}5>_{s}7>_{s}9\dots$

Następnie pojawiają się w tym porządku wszystkie liczby będące iloczynem dwójki i liczby nieparzystej (zaczynając od $2\cdot 3$ ), liczby postaci $2^{2}\cdot$ liczba nieparzysta etc.

Mamy więc

$3>_{s}5>_{s}7>_{s}9>_{s}\dots>_{s}2\cdot 3>_{s}2\cdot 5>_{s}2\cdot 7>_{s}\dots>_{s}2^{2}\cdot 3>_{s}s^{2}\cdot 5>_{s}2^{2}\cdot 7>_{s}\dots>_{s}2^{n}\cdot 3>_{s}2^{n}\cdot 5>_{s}\dots$

W ten sposób uporządkowane zostały wszystkie liczby poza potęgami dwójki. Ustawiamy je na końcu, w porządku malejącym

$\dots>_{s}2^{3}>_{s}2^{2}>_{s}2^{2}>_{s}2^{1}>_{s}2^{0}=1$

Zatem: największą liczbą w tym porządku jest $3$ , zaś najmniejszą $1$ .

Możemy teraz sformułować

Twierdzenie 4.2

Twierdzenie Szarkowskiego.

Niech $f:I\to\mathbb{R}$ będzie funkcją ciągłą. Wówczas, jeśli $f$ ma punkt o okresie (podstawowym) $n$ , to $f$ ma punkty o wszystkich okresach mniejszych (w porządku Szarkowskiego) od $n$ .

Uwaga 4.1

Oczywiście twierdzenie 4.1 jest szczególnym przypadkiem twierdzenia Szarkowskiego. Liczba $3$ jest największa w porządku Szarkowskiego, zatem istnienie punktu o okresie $3$ implikuje istnienie punktów o wszystkich innych okresach.

4.3. Bifurkacja podwajania okresu. Obserwacja Feigenbauma

Z twierdzenia Szarkowskiego wynika że istnienie jednych orbit okresowych wynika istnienie innych i ze ”najwczesniejszymi” orbitami okresowymi sa orbity o okresach będących potęgami $2$ . W ”modelowej” rodzinie przekształeceń odcinka $x\mapsto ax(1-x)$ , $a\in[0,4]$ obserwujemy pojawianie się kolejnych orbit okresowych o okresach $2^{n}$ ; dokładniej- bifurkacja polega na tym że orbita okresowa przyciągająca o okresie $2^{{n-1}}$ staje się odpychająca (pochodna iteracji ma moduł większy od $1$ ), a blisko niej - tworzy się nowa orbita przyciągająca, o dwukrotnie dluższym okresie. Niech $a_{n}$ oznacza parametr w którym pojawia się orbita okresowa o okresie $2^{n}$ . Feigenbaum zauważył (choć nie umiał tego udowodnić) że ilorazy

$\frac{a_{{n+1}}-a_{n}}{a_{n}-a_{{n-1}}}$

(4.1)

mają prawdopodobnie granicę. Zauważył też że ta granica pozostaje niezmieniona gdy rodzinę funkcji $x\mapsto ax(1-x)$ zastąpił inną rodziną. Tę wspólną granicę ciągów (4.1) nazywa się stałą Feigenbauma.

Badania nad wyjaśnieniem tego zjawiska doprowadziły do rozpatrywania tzw. operatora renormalizacji (zdefiniowanego w odpowiedniej przestrzeni funkcji), wykazania istnienia punktu stałego dla tego operatora i hiperboliczności tego punktu stałego, oraz badania tzw rozmaitości stabilnej w tym punkcie. (Pojęcie hiperboliczności i rozmaitości stabilnych dla przekształceń określonych w $\mathbb{R}^{m}$ bądź na rozmaitości pojawi sie w następnych rozdziałach; opis problemu renormalizacji wykracza jednak poza zakres tego wykładu).

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Wstęp do teorii Układów Dynamicznych