Zagadnienia

5.1 Zachowanie asymptotyczne trajektorii. Zbiór $\omega$ -graniczny.
5.2 Pola gradientowe
5.3 Cięcia transwersalne i przekształcenie Poincare'go w otoczeniu orbity okresowej

5. Pola wektorowe na rozmaitościach. Zbiory graniczne i zbiór punktów niebłądzących. Pola gradientowe

Będziemy mówili o trajektoriach pola wektorowego na rozmaitości $M$ zanurzonej w $\mathbb{R}^{n}$ . Będziemy również zakładali że rozmaitość $M$ jest zwarta. Z twierdzenia o przedłużaniu rozwiązań wynika że wówczas potok pola wektorowego $\phi^{t}$ jest określony dla wszystkich czasów $t\in\mathbb{R}$ . Mamy więc jednoparametrową rodzinę dyfeomorfizmów określonych na rozmiatości $M$ .

Duża część rozważań ma jednak charakter lokalny, więc wystarczy wtedy wykazać odpowiednie twierdzenia dla pola określonego na otwartym podzbiorze $\mathbb{R}^{m}$ i skorzystać z następującej obserwacji:

Stwierdzenie 5.1 (O trajektoriach pola w parametryzacji)

Niech $X$ będzie polem wektorowym określonym na gładkiej, $m$ -wymiarowej rozmaitości $M$ zanurzonej w $\mathbb{R}^{n}$ . Niech $\psi$ bedzie parametryzacją otwartego podzbioru $M$ . $\psi$ jest zatem określone na otwartym podzbiorze $\mathbb{R}^{m}$ . Rozważmy pole $Y=\psi^{*}X$ , czyli $Y$ określone na otwartym podzbiorze $\mathbb{R}^{m}$ wzorem:

$Y(p)=\psi^{*}X(p)=\left(D\psi(p)\right)^{{-1}}\left(X(\psi(p))\right)$

Wówczas $c(t)$ jest krzywą całkową równania $\dot{x}=X(x)$ wtedy i tylko wtedy gdy $\tilde{c}(t)=\psi\circ c(t)$ jest krzywą całkową równania $\dot{x}=X(x)$ .

Załóżmy że:

$\frac{d}{dt}c(t)=Y(c(t))$

Sprawdzamy że

$\frac{d}{dt}\tilde{c}(t)=X(\tilde{c}(t))$

Mamy

$\frac{d}{dt}\psi(c(t))=D\psi(c(t))(\dot{c}(t))=D\psi(c(t))(Y(c(t))=(D\psi\circ Y)(c(t))=X(c(t))$

Dowód odwrotnej implikacji jest analogiczny.

∎

5.1. Zachowanie asymptotyczne trajektorii. Zbiór $\omega$ -graniczny.

Definicja 5.1

Niech $X$ bedzie polem wektorowym na rozmaitości gładkiej zwartej $M$ , $\phi^{t}$ - potokiem tego pola. Mówimy że $y\in M$ jest punktem $\omega$ - granicznym trajektorii $x$ , $y\in\omega(x)$ jeśli istnieje ciąg czasów $t_{n}\to\infty$ taki że

$\phi^{{t_{n}}}(x)\to y.$

Twierdzenie 5.1 (Własności zbioru $\omega$ -granicznego)

Niech $X$ będzie polem wektorowym klasy $C^{r}$ na zwartej rozmaitości $M$ . Niech $p\in M$ . Wówczas:

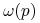$\omega(p)\neq\emptyset$
$\omega(p)$ jest domkniętym podzbiorem $M$ .
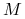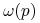$\omega(p)$ jest niezmienniczym (ze względu na potok pola 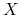$X$ ) podzbiorem 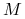$M$ , to znaczy 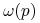$\omega(p)$ jest sumą pewnych trajektorii pola $X$ .
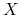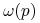$\omega(p)$ jest zbiorem spójnym.

Pierwsza własność wynika natychmiast ze zwartości $M$ . Druga własność wynika z następującej obserwacji: jeśli $\varphi _{t}$ jest potokiem pola $X$ i $\varphi _{{t_{n}}}(p)\to q$ dla pewnego ciągu $t_{n}\to\infty$ , to

$\varphi _{{t_{n}+t_{0}}}(p)=\varphi _{{t_{0}}}(\varphi _{{t_{n}}}(p)\to\varphi _{{t_{0}}}(q),$

zatem $\varphi _{{t_{0}}}(q)\in\omega(p)$ . Spójność wykażemy niewprost: załózmy że $\omega(p)$ jest sumą dwóch rozłącznych domkniętych zbiorów $\omega(p)=A\cup B$ . Ponieważ są to domknięte rozłaczne podzbiory, możemy znależć otoczenia $V_{1}\supset A$ , $V_{2}\supset B$ takie że $\overline{V_{1}}\cap\overline{V_{2}}=\emptyset$ . Ponieważ $A\subset\omega(p)$ więc istnieje ciąg $t_{n}\to\infty$ taki że $\varphi _{{t_{n}}}(p)\in V_{1}$ . Ponieważ $B\subset\omega(p)$ , dla każdego $t_{n}$ znajdzie się $t^{{\prime}}_{{n}}>t_{n}$ taki że $\varphi _{{t^{{\prime}}_{n}}}(p)\notin\{ V_{1}\cup V_{2}$ . Zatem (pamietamy że $M\setminus(v_{1}\cup V_{2})$ jest zwarty) istnieje punkt $q\in\omega(p)$ w $V_{1}\cup V_{2}$ . Otrzymujemy sprzeczność.

∎

Przykład 5.1 (Obmotka na torusie)

Rozpatrzmy stałe pole wektorowe na $\mathbb{R}^{2}$ : $X(x,y)=(a,b)$ . Trajektorie tego pola w $\mathbb{R}^{2}$ to oczywiście proste $(x(t),y(t)=(x_{0},y_{0})+t(a,b)$ . To samo pole można rozważać na torusie - przestrzeni ilorazowej $\mathbb{T}^{2}=\mathbb{R}^{2}/\mathbb{Z}^{2}$ . Trajektoriami na torusie są linie powstałe jako rzutowania prostych $(x(t),y(t)=(x_{0},y_{0})+t(a,b)$ . Jeślli iloraz $\frac{a}{b}$ jest liczbą wymierną tokażda trajektoria na torusie jest okresowa. Jeśli iloraz jest niewymierny to każda trajektoria jest gęsta. W tym drugim przypadku mamy: $\omega(x)=\mathbb{T}^{2}$ dla każdego $x\in\mathbb{T}^{2}$ .

Definicja 5.2 (Zbiór punktów niebłądzących 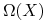$\Omega(X)$ .)

Mówimy że punkt $x\in M$ jest błądzący jeśli istnieje jego otoczenie $U$ i $t_{0}>0$ że dla każdego $t>t_{0}$ mamy $\varphi^{t}(U)\cap U=\emptyset$ . Uzupelnienie zbioru punktów błądzących nazywamy zbiorem punktów niebłądzących i oznaczamy $\Omega(X)$ .

Uwaga 5.1

Zbiór $\Omega(X)$ jest niezmienniczy ze względu na dzialanie pola $X$ (tzn $\varphi^{t}(\Omega(X))=\Omega(X)$ ) i domknięty.

Uwaga 5.2

Oczywiście zbiór $\omega(x)$ jest zawarty w $\Omega(X)$ .

5.2. Pola gradientowe

Przykład- potoki gradientowe

Niech $M$ będzie gładką $m$ - wymiarową podrozmaitością zanurzoną w $\mathbb{R}^{n}$ . W przestrzeni stycznej do $M$ mamy zdefiniowany iloczyn skalarny i normę dziedziczoną z $\mathbb{R}^{n}$ . (Mamy więc strukturę Riemannowska dziedziczona z $\mathbb{R}^{n}$ ).

Niech $f:M\to\mathbb{R}$ będzie funkcją klasy $C^{{r+1}}$ . Wówczas różniczka $f$ w punkcie $p\in M$ , $d_{p}f$ jest $1$ - formą (przekształceniem liniowym $T_{p}M\to\mathbb{R}$ . Zatem istnieje dokładnie jeden wektor $X(p)$ w przestrzeni stycznej $T_{p}M$ , taki że $d_{p}f(v)=\left<X(p),v\right>$ . Ten wektor nazywamy gradientem funkcji $f$ w punkcie $p$ . Otrzymujemy w ten sposób pole wektorowe klasy $C^{r}$ na $M$ . Jeśli funkcja $f$ jest określona nie tylko w $M$ , ale również na otoczeniu $M$ w $\mathbb{R}^{n}$ , to łatwo można związać gradient $f_{{|M}}$ ze zwykłym wektorem gradientu w $\mathbb{R}^{n}$ . Możemy policzyć ”zwykłą” różniczkę $f$ w $\mathbb{R}^{n}$ , $Df$ , i ”zwykły” gradient $Grad(f)=(\frac{\partial f}{\partial x_{1}},\dots\frac{\partial f}{\partial x_{n}})$ . Wówczas dla $v\in T_{p}M$

$df(v)=Df(v)=\left<v,Gradf\right>=\left<v,v_{n}+v_{{st}}\right>=\left<v,v_{{st}}\right>$

Zatem $gradf$ (gradient $f$ ”wzdłuż” rozmaitości $M$ jest rzutem prostopadłym gradientu policzonego w przestrzeni $\mathbb{R}^{n}$ , $Gradf$ , na przestrzeń styczną do $M$ .

Definicja 5.3

Punkt $q$ jest punktem osobliwym pola wektorowego $X$ jeśli $X(q)=0$ .

Stwierdzenie 5.2 (Własności pola gradientowego)

Niech $M\subset\mathbb{R}^{n}$ będzie gładką rozmaitością, $f:M\to\mathbb{R}$ -funkcją klasy $C^{{r+1}}$ na $M$ ,zaś $X=gradf$ - gradientowym polem wektorowym (klasy $C^{r}$ na $M$ . Wówczas

Pole gradientowe 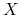$X$ nie ma trajektorii zamkniętych.
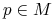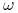Dla każdego $p\in M$ zbiór $\omega$ - graniczny 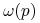$\omega(p)$ jest zawarty w zbiorze punktów osobliwych pola $X$ .

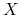Zauważmy że dla każdej trajektorii pola $\phi^{t}(x)$ mamy:

$\frac{d}{dt}f(\phi^{t}(x)=df(\dot{\phi}^{t}(x))=df(gradf(\phi^{t}(x)=<gradf(\phi^{t}(x)),gradf(\phi^{t}(x))>\ge 0.$

Zatem funkcja $f$ jest niemalejąca wzdłuż każdej trajektorii, a dokładniej- ściśle rosnąca wzdłuż każdej ”niestacjonarnej trajektorii”.

Wynika stąd oczywiście że pole nie ma orbit zamkniętych.

Załóżmy teraz że punkt $y\in\omega(x)$ i $X(y)\neq 0$ . Wowczas w otoczeniu punktu $y$ poziomica $N$ funkcji $f$ przechodząca przez $y$ jest podrozmaitością $M$ prostopadła do linii pola $X$ . Z twierdzenia o prostowaniu trajektorii wynika że każda trajektoria pola startujaca dostatecznie blisko punktu $y$ musi przeciąć poziomicę $N$ . Jeśli $y\in\omega(x)$ to trajektoria $x$ , $\phi^{t}(x)$ musi zatem przeciąć nieskończenie wiele razy poziomicę $N$ . Ponieważ jednak, jak już wiemy, funkcja $f$ jest ściśle rosnąca wzdłuż tej trajektorii, jest to oczywiście niemożliwe.

∎

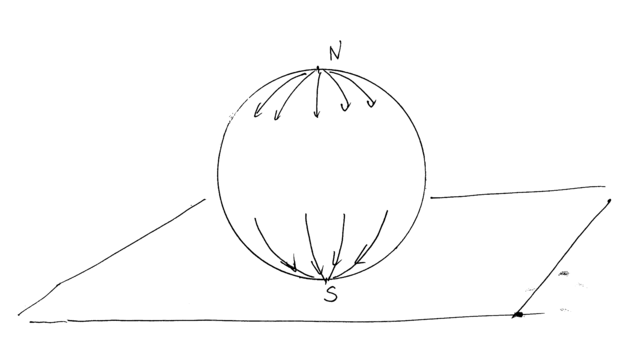
Przykład 5.2

Pole gradient wysokości na sferze. To pole ma dwa punkty osobliwe $N$ i $S$ . Punkt $N$ jest źródłem, punkt $S$ -ściekiem. Dla każdego punktu $x\neq N$ mamy $\omega(x)=\{ S\}$ (rysunek 5.1)

Pole gradient wysokości na sferze dwuwymiarowej

Rys. 5.1. Gradient wysokości na sferze.

Przykład 5.3

Pole wektorowe gradientowe na postawionym torusie. Tu $f(x,y,z)=-z$ . To pole ma cztery punkty stacjonarne: $N,S,R,Q$ . $N$ jest źródłem, $S$ -ściekiem, $R,Q$ - siodłami. Zauważmy że tym razem zbiór $\omega$ - graniczny zależy od punktu, w szczególności istnieją punkty dla ktorych $\omega(x)$ jest siodłem. Istnieja też połączenia między siodlami- trajektorie $\phi^{t}(x)$ takie że dla $t\to-\infty$ $\phi^{t}(x)\to R$ , zaś dla $t\to\infty$ $\phi^{t}(x)\to Q$ . (rysunek 5.2).

Pole gradient wysokości na torusie dwuwymiarowym

Rys. 5.2. Gradient wysokości na torusie.

5.3. Cięcia transwersalne i przekształcenie Poincare'go w otoczeniu orbity okresowej

Rozważmy pole wektorowe $X$ klasy $C^{r}$ określone (dla uproszczenia) w otwartym podzbiorze $\mathbb{R}^{m}$ . Niech $\gamma$ będzie zamkniętą trajektorią tego pola, $t_{0}$ - okresem tej trajektorii, $p\in\gamma$ . Możemy założyć że $X_{m}(p)\neq 0$ . Rozważmy hiperpowierzchnię $\Sigma=\{ x:x_{m}=p_{m}\}$ . Zatem pole jest w punkcie $p$ transwersalne do $\Sigma$ . Dla $x$ bliskich $p$ trajektoria pola wychodząca z $x$ wróci po czasie bliskim $t_{0}$ do $\Sigma$ . Formalne sprawdzenie: Niech $\varphi^{t}$ będzie potokiem pola $X$ , określamy funkcję

$\Psi(x,t)=\varphi^{t}_{m}(x)-p_{m}$

Wówczas $\psi(t,x)=0\iff\varphi^{t}(x)\in\Sigma$ i $\psi(t_{0},p)=0$ .

Mamy

$\frac{\partial}{\partial t}\psi(x,t)_{{(p,t_{0})}}=\frac{\partial}{\partial t}\varphi^{t}_{m}(x)_{{(p,t_{0})}}=X_{m}(p)\neq 0$

Zatem- z twierdzenia o funkcji uwikłanej wynika że istnieje otoczenie $(p,t_{0})$ w $\Sigma\times\mathbb{R}$ w którym to równanie wyznacza $t$ jako funkcję $x$ , tej samej klasy co $X$ . Oznaczamy tę funkcję $\tau(x)$ .

Mamy więc w otoczeniu $p$ w $\Sigma$ zdefiniowane przekształcenie klasy $C^{r}$ :

$x\mapsto\varphi^{{\tau(x)}}(x)$

Nazywamy je przekształceniem Poincare'go, oznaczenie: $P_{p}$ .

Pytamy o związek między wartościami własnymi dla pochodnej przekształcenia Poincare'go w punkcie $p$ i różniczki potoku pola: $D\varphi^{{t_{0}}}(p)$ .

Wiemy już że jedną z wartości własnych $D\varphi^{{t_{0}}}(p)$ jest $1$ , bo $D\varphi^{{t_{0}}}(p)(X(p))=X(p)$ .

Twierdzenie 5.2

Wartości własne różniczki $D\varphi^{{t_{0}}}(p)$ , różne od $1$ , są takie same jak wartości własne rózniczki $DP_{p}(p)$ .

W $R^{m}$ wprowadzamy układ współrzędnych, w którym jednym z wektorów bazowych jest $X(p)$ , a pozostałe wektory- to baza $\Sigma$ . Weźmy wektor styczny dla $\Sigma$ , ma on postać (w układzie współrzędnych w $\mathbb{R}^{m}$ z wyróżnioną ostatnią współrzędną) $(v,0)$ . Różniczka $D\varphi^{{t_{0}}}$ w tej bazie to

$D\varphi^{{t_{0}}}=\left(\begin{array}[]{rrrr}A&0\\ \alpha&1\\ \end{array}\right)$

(5.1)

Tutaj $A$ jest macierzą $(n-1)\times(n-1)$ . Przekształcenie Poincarego $P(x)=\varphi(\tau(x),x)$ . Zatem

$D_{p}P(v,0)=X(p)D\tau(p)(v,0)+\frac{\partial\varphi}{\partial x}(p,\tau(p))(v,0)=X(p)D\tau(p)(v,0)+\left(\begin{array}[]{rrrr}A&0\\ \alpha&1\\ \end{array}\right)\left[\begin{array}[]{rrrr}v\\ 0\\ \end{array}\right]$

Skądinąd wiemy że obrazem $D_{p}P(v,0)$ musi byc wektor styczny do $\Sigma$ , więc współrzedna w kierunku pola $X$ znika i ostatecznie

$D_{p}P(v,0)=(Av,0)$

To zaś oznacza że $D_{p}P$ ma takie same wartości własne jak różne od $1$ wartości własne $D\varphi^{{t_{0}}}(p)$ .

∎

Definicja 5.4

Mówimy że orbita okresowa $\gamma$ , o okresie $t_{0}$ pola $X$ jest hiperboliczna jeśli dla punktu $p\in\gamma$ różniczka $D\varphi^{{t_{0}}}(p)$ ma tylko jedną -pojedynczą wartość własną równą $1$ . Równoważnie- jeśli dla cięcia Poincare'go $\Sigma$ różniczka przekształcenia Poincare'go $P$ nie ma wartości własnych różnych od $1$ .

Treść automatycznie generowana z plików źródłowych LaTeXa za pomocą oprogramowania wykorzystującego LaTeXML.

Wstęp do teorii Układów Dynamicznych